Work and Energy Class 9 Extra Questions and Answers Free PDF Download
FAQs on CBSE Important Questions for Class 9 Science Work and Energy - 2025-26
1. What are the most important types of questions to prepare from CBSE Class 9 Science Chapter 10, Work and Energy, for the 2025-26 exams?
For the 2025-26 exams, students should focus on a mix of question types from Chapter 10 to score well. The most important areas to prepare are:
- Conceptual Questions: Questions based on the definitions of work, energy, power, and the conditions for zero work.
- Derivations: The derivation of the formula for kinetic energy (KE = ½ mv²) is a frequently asked question.
- Numerical Problems: Practice numericals based on calculating work done (W = Fs cosθ), kinetic energy, potential energy (PE = mgh), power (P = W/t), and conversion of energy units.
- HOTS (High Order Thinking Skills): Questions based on the Law of Conservation of Energy, especially explaining energy transformations in real-world scenarios like a simple pendulum or a freely falling body.
2. What is the marking weightage for the unit 'Motion, Force and Work' in the Class 9 Science Paper 2025-26?
According to the latest CBSE curriculum for the 2025-26 session, the unit 'Motion, Force and Work' (which includes Chapter 10: Work and Energy) carries a total weightage of 27 marks in the final theory examination. This highlights the importance of mastering the concepts and numericals from this chapter.
3. Which numerical problems from the Work and Energy chapter are most expected in the Class 9 exam?
The most expected numerical problems from this chapter typically involve direct formula application. Key types to practise are:
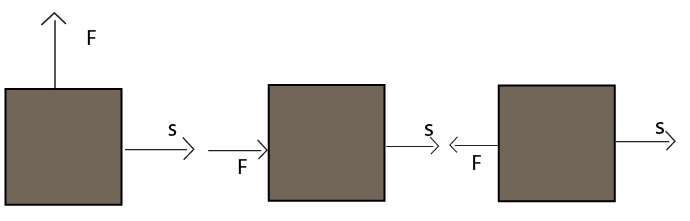
- Calculating work done when the force and displacement are given. Pay special attention to cases where the angle between force and displacement is 0°, 90°, or 180°.
- Calculating the kinetic energy of an object given its mass and velocity.
- Finding the potential energy of an object at a certain height.
- Problems involving the calculation of power, where you might first need to calculate the work done.
- Calculations based on the commercial unit of energy, converting kilowatt-hours (kWh) to joules and vice versa.
4. Is the derivation of the formula for kinetic energy an important question for the Class 9 exam?
Yes, deriving the expression for kinetic energy, KE = ½ mv², is a very important question, often appearing as a 3-mark or 5-mark question. You should be able to derive it using the third equation of motion (v² - u² = 2as) and the formula for work done (W = F × s). Mastering this derivation is crucial for scoring well.
5. If energy can neither be created nor destroyed, why does a bouncing ball eventually stop? Isn't this a violation of the Law of Conservation of Energy?
This is a classic conceptual trap and does not violate the Law of Conservation of Energy. While the total energy of the system remains constant, it is transformed into other forms. With each bounce, a part of the ball's mechanical energy (kinetic and potential) is converted into:
- Heat energy: Due to the deformation of the ball on impact with the ground.
- Sound energy: The 'thud' sound you hear is energy being radiated away.
- Work done against air resistance: As the ball moves through the air, it loses energy.
So, the ball stops because its initial mechanical energy is gradually dissipated as other, less useful forms of energy, not because energy is 'lost' or destroyed.
6. How can work done be zero even if a strong force is applied? Explain with an exam-oriented example.
Work done (W = Fs cosθ) is zero under two main conditions, even when a non-zero force (F) is applied. For an exam question, you should state:
- When displacement is zero (s = 0): If you push a rigid wall with all your might, you apply a large force, but the wall does not move. Since the displacement is zero, the work done on the wall is zero (W = F × 0 = 0).
- When force is perpendicular to displacement (θ = 90°): When a satellite orbits the Earth, the gravitational force acts towards the centre of the Earth, while its displacement at any instant is tangential to the orbit. The angle between the force and displacement is 90°. Since cos(90°) = 0, the work done by gravity on the satellite is zero.
7. What is the fundamental difference between potential and kinetic energy, and can an object possess both at the same time?
The fundamental difference lies in their cause:
- Potential Energy (PE) is the energy stored in an object due to its position or configuration (e.g., height in a gravitational field, or being stretched/compressed).
- Kinetic Energy (KE) is the energy an object possesses due to its motion.
Yes, an object can absolutely possess both simultaneously. A common example is a flying bird or an aeroplane. It has kinetic energy because it is moving, and it has potential energy because it is at a height above the ground.
8. Why is the commercial unit of energy (kWh) used for electricity bills instead of the SI unit, the Joule?
The Joule is the SI unit of energy, but it is a very small unit for measuring large-scale energy consumption like in households or industries. Using Joules would lead to extremely large and impractical numbers on electricity bills. The kilowatt-hour (kWh) is a much larger unit (1 kWh = 3.6 × 10⁶ Joules), making it more convenient and practical for commercial purposes. It directly relates power (in kW) and time (in hours), which is how electrical appliance usage is typically measured.