NCERT Exemplar for Class 12 Physics Chapter-5 (Book Solutions)

Exercise

MULTIPLE CHOICE QUESTIONS-I

5.1 A Toroid of n turns, mean radius R and cross-sectional radius a carries current I. It is placed on a horizontal table taken as x-y plane. Its magnetic moment m

(a) is non-zero and points in the z-direction by symmetry.

(b) points along the axis of the toroid $\left( {\overrightarrow M  = m\widehat \phi } \right)$ .

(c) is zero, otherwise there would be a field falling as $\dfrac{1}{{{r^3}}}$ at large distances outside the toroid.

(d) is pointing radially outwards.

Ans: Option (c) 

In the above case, since we know that there is no magnetic field existing outside the toroid. Hence the magnetic field falls very rapidly outside because it is inversely proportional to the third power of distance from the centre of the given toroid. Using the Ampere's circuital law, we can say that there is no current outside hence no magnetic moment exists at the outside. Hence, the correct answer is (c).

5.2 The magnetic field of Earth can be modelled by that of a point dipole placed at the centre of the Earth. The dipole axis makes an angle of 11.3° with the axis of Earth. In Mumbai, declination is nearly zero. Then,

(a) the declination varies between 11.3° W to 11.3° E.

(b) the least declination is 0°.

(c) the plane defined by the dipole axis and Earth's axis passes through Greenwich.

(d) declination averaged over Earth must be always negative.

Ans: Option (a) 

Given that, the axis of the dipole is tilted 11.3° with the axis of earth by 11.3° at both sides, i.e. east and west. Hence, this declination varies from the direction of East to West from both sides by 11.3° on the earth’s surface. Therefore, the correct answer is (a).

5.3 In a permanent magnet at room temperature

(a) The magnetic moment of each molecule is zero.

(b) the individual molecules have non-zero magnetic moments which are all perfectly aligned.

(c) domains are partially aligned.

(d) domains are all perfectly aligned.

Ans: Option (c) 

At room temperature, a permanent magnet behaves like a ferromagnetic substance where its domains are permanently partially aligned. Hence, the correct answer is (c).

5.4 Consider the two idealized systems: (i) a parallel plate capacitor with large plates and small separation and (ii) a long solenoid of length L >> R, radius of cross-section. In (i) E is ideally treated as a constant between plates and zero outside. In (ii) magnetic field is constant inside the solenoid and zero outside. These idealized assumptions, however, contradict fundamental laws as below:

(a) case (i) contradicts Gauss’s law for electrostatic fields.

(b) case (ii) contradicts Gauss’s law for magnetic fields.

(c) case (i) agrees with $\oint_s {E \cdot dl = 0} $ .

(d) case (ii) contradicts $\oint {H \cdot dl}  = {\rm I}$ .

Ans: Option (b) 

Here, according to the Gauss’s law of electrostatic field, we have $\oint_s {E \cdot ds = \dfrac{q}{{{\varepsilon _0}}}} $ . In this case, the electric field lines do not form a continuous path, hence it does not contradict with the electrostatic field. Also, according to Gauss’s law of magnetic field, we have $\oint_s {B \cdot ds = 0} $ . Now since there is a magnetic field formed inside the solenoid, and no field outside the solenoid that is carrying current, but the magnetic field lines are forming closed paths. Therefore, it contradicts the magnetic field. Hence, the correct answer is (b).

5.5 A paramagnetic sample shows a net magnetisation of $8A{m^{ - 1}}$ when placed in an external magnetic field of 0.6T at a temperature of 4K. When the same sample is placed in an external magnetic field of 0.2 T at a temperature of 16K, the magnetisation will be-

(a) $\dfrac{{32}}{3}A{m^{ - 1}}$

(b) $\dfrac{2}{3}A{m^{ - 1}}$v

(c) $6A{m^{ - 1}}$

(d) $2.4A{m^{ - 1}}$

Ans: Option (b)  

According to Curie's law, the magnetization of a paramagnetic material is directly proportional to the applied magnetic field. Also, if the material is heated, the magnetization becomes inversely proportional to the given temperature, i.e $I \propto \dfrac{B}{T}$

Therefore, we can write the ratio of the two magnetization as $\dfrac{{{I_2}}}{{{I_1}}} = \dfrac{{{B_2}{T_1}}}{{{B_1}{T_2}}}$

That gives us, $I = {I_1}\dfrac{{{B_2}{T_1}}}{{{B_1}{T_2}}} = 8 \cdot \dfrac{{\left( {0.2} \right) \cdot 4}}{{\left( {0.6} \right) \cdot 16}} = \dfrac{2}{3} = 0.66A{m^{ - 1}}$

Hence, the correct answer is (b).

MULTIPLE CHOICE QUESTIONS-II MORE THAN ONE OPTION

5.6 S is the surface of a lump of magnetic material.

(a) Lines of B are necessarily continuous across S.

(b) Some lines of B must be discontinuous across S.

(c) Lines of H are necessarily continuous across S.

(d) Lines of H cannot all be continuous across S.

Ans: Options (a) and (d)

Magnetic field lines are continuous lines hence they are continuous across S. Also, the lines of magnetic intensity H vary inside and outside so they cannot all be continuous across S. Hence, the correct answers are (a) and (d).

5.7 The primary origin(s) of magnetism lies in

(a) atomic currents.

(b) Pauli exclusion principle.

(c) polar nature of molecules.

(d) intrinsic spin of electron.

Ans: Options (a) and (d)

Magnetic fields are generally formed due to the magnetic effect of electric current which happens due to the revolution and spin of electrons around the nucleus. Hence, the correct answers are (a) and (d).

5.8 A long solenoid has 1000 turns per metre and carries a current of 1 A. It has a soft iron core of ${\mu _r} = 1000$. The core is heated beyond the Curie temperature, ${T_c}$ .

(a) The H field in the solenoid is (nearly) unchanged but the B field decreases drastically.

(b) The H and B fields in the solenoid are nearly unchanged.

(c) The magnetisation in the core reverses direction.

(d) The magnetisation in the core diminishes by a factor of about ${10^8}$ .

Ans: Options (a) and (d)

We are given that, ${\mu _r} = 1000$ and $n = 1000$

Now, we have $H = nI = 1000 \times 1 = 1000Amp$

That means H is constant.

Now since we can write $B = {\mu _0}{\mu _r}nI = \left( {{\mu _0}nI} \right){\mu _r} = K{\mu _r}$

Hence, $B \propto {\mu _r}$

Now according to the Curie’s law, ferromagnetic substances start to behave like paramagnetic substances if heated above the Curie temperature.

Now we have, susceptibility of ${\left( {{X_m}} \right)_{ferro}} = {10^3}$ and ${\left( {{X_m}} \right)_{para}} = {10^{ - 5}}$

Therefore, $\dfrac{{{B_1}}}{{{B_2}}} = \dfrac{{{x_2}}}{{{x_1}}} = \dfrac{{{{10}^{ - 5}}}}{{{{10}^3}}} = {10^{ - 8}}$

That gives ${B_1} = {10^{ - 8}}{B_2}$

Hence, the correct answers are (a) and (d).

5.9 Essential difference between electrostatic shielding by a conducting shell and magnetic shielding is due to

(a) electrostatic field lines can end on charges and conductors have free charges.

(b) lines of B can also end but conductors cannot end them.

(c) lines of B cannot end on any material and perfect shielding is not possible.

(d) shells of high permeability materials can be used to divert lines of B from the interior region.

Ans: Options (a),(c) and (d)

The lines of electrostatic fields can be stopped by conductors giving shielding effect due to their free charge particles. Also, the magnetic field lines cannot be stopped or shielded but they are affected by magnetic material because they can be repelled using a high permeability magnetic material. Hence, the correct answers are (a), (c) and (d).

5.10 Let the magnetic field on earth be modelled by that of a point magnetic dipole at the centre of earth. The angle of dip at a point on the geographical equator

(a) is always zero.

(b) can be zero at specific points.

(c) can be positive or negative.

(d) is bounded.

Ans: Options (b),(c) and (d)

At its equatorial plane of dipole, the resultant magnetic field due to dipole will be zero but not on the geographical equator. Also, it can be positive and negative but it is bounded. Hence, the correct answers are (b), (c) and (d).

VERY SHORT ANSWER TYPE QUESTIONS

5.11 A proton has spin and magnetic moment just like an electron. Why then its effect is neglected in magnetism of materials?

Ans: The ratio of magnetic moments of proton and electron is $\dfrac{1}{{1836}}$ , i.e. it is very less compared to the magnetic moment of an electron and hence it is neglected in magnetism of materials.

5.12. A permanent magnet in the shape of a thin cylinder of length 10 cm has $M = {10^6}A/m$ . Calculate the magnetisation current ${I_M}$ .

Ans: Given that, $M = {10^6}A/m$ and $l = 10cm = 0.1m$

Hence we have, ${I_M} = Ml = {10^6} \times 0.1 = {10^5}A$

5.13 Explain quantitatively the order of magnitude difference between the diamagnetic susceptibility of ${N_2}\left( { \sim 5 \times {{10}^{ - 9}}} \right)$ (at STP) and $Cu\left( { \sim {{10}^{ - 5}}} \right)$ .

Ans: The ratio of densities of Nitrogen and Copper is given by, $\dfrac{{{\rho _N}}}{{{\rho _{Cu}}}} = \dfrac{{28g/22.4L}}{{8g/c{m^3}}} = \dfrac{{3.5}}{{22.4}} \times {10^{ - 3}} = 1.6 \times {10^{ - 4}}$

Now since we know that the susceptibility of a diamagnetic material is given by the intensity of magnetization divided by its magnetizing force, i.e. $x = \dfrac{I}{H}$

Also, magnetic intensity is defined as the magnetic moment per unit volume of the magnetised material, hence $I = \dfrac{M}{V}$

Now, that gives us the expression of susceptibility as $x = \dfrac{M}{{HV}}$

Also, $V = \dfrac{m}{\rho }$ so we have $x = \dfrac{M}{{Hm}} \cdot \rho $

Hence, $x \propto \rho $ i.e. the diamagnetic susceptibility is directly proportional to the density of a material.

Also by the given data, we can write the ratio of their diamagnetic susceptibilities as, $\dfrac{{{x_N}}}{{{x_{Cu}}}} = \dfrac{{5 \times {{10}^{ - 9}}}}{{{{10}^{ - 5}}}} = 5 \times {10^{ - 4}}$

This major difference is due to their difference in densities.

5.14 From the molecular view point, discuss the temperature dependence of susceptibility for diamagnetism, Paramagnetism and ferromagnetism.

Ans: The susceptibility of diamagnetism is not much affected by temperature because the direction of external magnetic field H and magnetism M due to orbital motion of electrons of diamagnetic substance are opposite so net magnetism becomes zero.

The net magnetism is increased and is much affected by temperature in paramagnetic and ferromagnetic material because the direction of magnetism due to orbital motion of electrons and the external applied field are in the same direction.

5.15 A ball of superconducting material is dipped in liquid nitrogen and placed near a bar magnet.

(i) In which direction will it move?

Ans: Both liquid nitrogen and any superconducting material are diamagnetic in nature and they remain diamagnetic when mixed together. Hence, when superconducting material dipped in liquid nitrogen comes across an external magnetic field then it will be repelled by that external magnetic field.

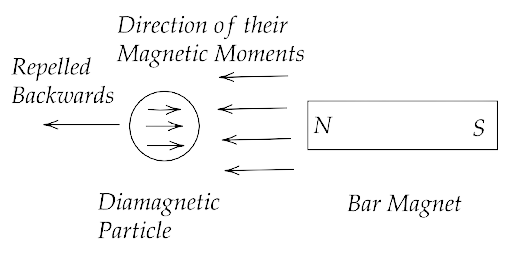
Therefore, the direction of motion will be opposite to the direction of the magnet.

(ii) What will be the direction of its magnetic moment?

Ans: Also, from the above figure we can say that the direction of the magnetic moment of the diamagnetic particle is opposite to the direction of the magnetic field induced by the bar magnet.

SHORT ANSWER TYPE QUESTIONS

5.16 Verify Gauss's law for the magnetic field of a point dipole of dipole moment $\overrightarrow m $ at the origin for the surface which is a sphere of radius R.

Ans: According to the Gauss’s law of magnetism, we have $\oint_s {\overrightarrow B  \cdot d\overrightarrow s  = 0} $

The magnetic moment (m) of a dipole at the origin O is given by $\overrightarrow m  = m\widehat k$

Now consider a point P at a distance r from the origin O and OP makes an angle $\theta $ with the z axis.

Also, the component of $\overrightarrow m $ along OP is equal to $\overrightarrow m \cos \theta $ .

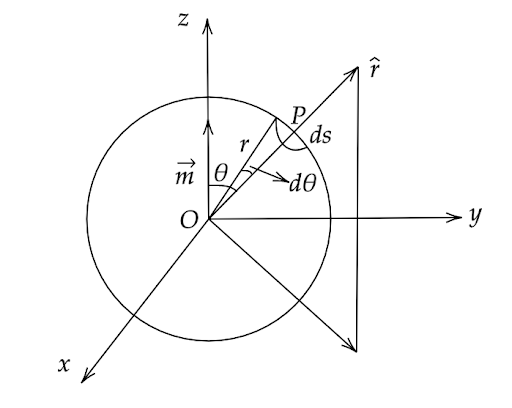
Where $r$ is the radius of the sphere with centre ‘O’ lying in the X-Y-Z plane. Centre at origin. Now, we can write the magnetic field of induction at point P due to the dipole of moment $\overrightarrow m \cos \theta $ as,

$ \Rightarrow B = \dfrac{{{\mu _0}}}{{4\pi }} \cdot \dfrac{{2\overrightarrow m \cos \theta }}{{{r^3}}}\widehat r$

Now if we take an elementary area ds at P then we have,

$ \Rightarrow d\overrightarrow s  = r\left( {r\sin \theta } \right)d\theta \widehat r = {r^2}\sin \theta d\theta \widehat r$

Hence, 

$ \Rightarrow \oint_s {\overrightarrow B  \cdot d\overrightarrow s }  = \oint_s {\dfrac{{{\mu _0}}}{{4\pi }} \cdot \dfrac{{2\overrightarrow m \cos \theta }}{{{r^3}}}\widehat r}  \cdot \left( {{r^2}\sin \theta d\theta \widehat r} \right)$

$ \Rightarrow \oint_s {\overrightarrow B  \cdot d\overrightarrow s }  = \dfrac{{{\mu _0}\overrightarrow m }}{{4\pi r}}\int\limits_0^{2\pi } {2\sin \theta \cos \theta d\theta } $

That gives us,

$ \Rightarrow \oint_s {\overrightarrow B  \cdot d\overrightarrow s }  = \dfrac{{{\mu _0}\overrightarrow m }}{{4\pi r}}\int\limits_0^{2\pi } {\sin 2\theta d\theta } $

$ \Rightarrow \oint_s {\overrightarrow B  \cdot d\overrightarrow s }  = \dfrac{{{\mu _0}}}{{4\pi r \times 2}}\left[ { - \cos 0 + 1} \right]$

That is,

$ \Rightarrow \oint_s {\overrightarrow B  \cdot d\overrightarrow s }  = \dfrac{{{\mu _0}}}{{4\pi r \times 2}}\left[ { - 1 + 1} \right]$

Hence,

$ \Rightarrow \oint_s {\overrightarrow B  \cdot d\overrightarrow s }  = 0$

This proves Gauss's law of magnetism.

5.17 Three identical bar magnets are riveted together at centre in the same plane as shown in Fig. 5.1. This system is placed at rest in a slowly varying magnetic field. It is found that the system of magnets does not show any motion. The north-south poles of one magnet is shown in the Fig. 5.1. Determine the poles of the remaining two.

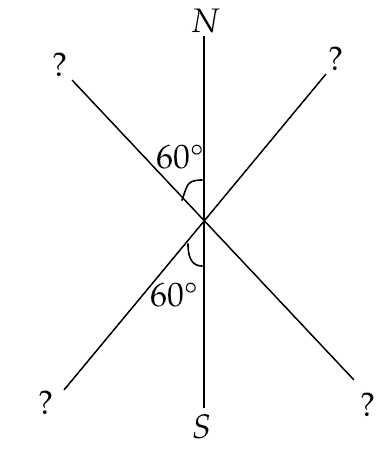
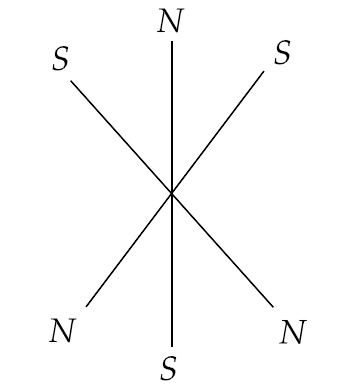
Ans: The given system of magnets is not showing any motion. This is possible only when each pole of these magnets is attracted by another magnet by both sides equally so that they do not move in one direction. When they are attracted by both sides with equal forces then they cannot move in any direction. Hence the accurate position of the other two magnets can be shown by the figure given below.

5.18 Suppose we want to verify the analogy between electrostatic and magnetostatic by an explicit experiment. Consider the motion of

(i) electric dipole $\overrightarrow p $ in an electrostatic field $\overrightarrow E $ and (ii) magnetic dipole $\overrightarrow m $ in a magnetic field $\overrightarrow B $ . Write down a set of conditions on $\overrightarrow E $ , $\overrightarrow B $ , $\overrightarrow p $ , $\overrightarrow m $ so that the two motions are verified to be identical. (Assume identical initial conditions.)

Ans: Let the angle between $\overrightarrow m $ and $\overrightarrow B $ be $\theta $ 

Then the torque on magnetic dipole in a magnetic field $\overrightarrow B $ is given by

$ \Rightarrow \tau  = \overrightarrow m \overrightarrow B \sin \theta $ ...(1)

Similarly, if the angle between $\overrightarrow p $ and $\overrightarrow E $ is $\theta $

Then the torque on electric dipole in a electric field $\overrightarrow E $ is given by

$ \Rightarrow \tau ' = \overrightarrow p \overrightarrow E \sin \theta $ ...(2)

Now if $\tau ' = \tau $

Then

$ \Rightarrow \overrightarrow m \overrightarrow B \sin \theta  = \overrightarrow p \overrightarrow E \sin \theta $

That gives,

$ \Rightarrow \overrightarrow m \overrightarrow B  = \overrightarrow p \overrightarrow E $

Since, $\overrightarrow E  = \overrightarrow c \overrightarrow B $

Hence,

$ \Rightarrow \overrightarrow m \overrightarrow B  = \overrightarrow p \overrightarrow c \overrightarrow B $

That gives us,

$ \Rightarrow \overrightarrow p  = \dfrac{{\overrightarrow m }}{{\overrightarrow c }}$

That is the required relation between $\overrightarrow m $ and $\overrightarrow p $.

5.19 A bar magnet of magnetic moment $\overrightarrow m $ and moment of inertia I (about centre, perpendicular to length) is cut into two equal pieces, perpendicular to length. Let T be the period of oscillations of the original magnet about an axis through the midpoint, perpendicular to length, in a magnetic field B. What would be the similar period T′ for each piece?

Ans: Since the magnet is cut into two equal parts, hence the magnetic moment of each part is $m' = \dfrac{m}{2}$ and length and mass of the each part will be $l' = \dfrac{l}{2}$ and $M' = \dfrac{M}{2}$

Also the original time period will be $T = 2\pi \sqrt {\dfrac{I}{{mB}}} $ where $I = \dfrac{{M{l^2}}}{{12}}$

Therefore $I' = \dfrac{{\left( {\dfrac{M}{2}} \right){{\left( {\dfrac{l}{2}} \right)}^2}}}{{12}} = \dfrac{{M{l^2}}}{{8 \times 12}}$

That gives us $\dfrac{{I'}}{I} = \dfrac{1}{8}$ and also $\dfrac{m}{{m'}} = \dfrac{m}{{\dfrac{m}{2}}} = \dfrac{2}{1}$

Now, 

$ \Rightarrow \dfrac{T}{{T'}} = \dfrac{{2\pi \sqrt {\dfrac{I}{{mB}}} }}{{2\pi \sqrt {\dfrac{{I'}}{{m'B}}} }} = \dfrac{{\sqrt {Im'} }}{{\sqrt {I'm} }}$

That is,

$ \Rightarrow \dfrac{T}{{T'}} = \sqrt {\dfrac{8}{1} \times \dfrac{1}{2}}  = \sqrt 4  = 2$

Hence, 

$ \Rightarrow T = 2T'$

And,

$ \Rightarrow T' = \dfrac{T}{2}$

5.20 Use (i) the Ampere’s law for $\overrightarrow H $ and (ii) continuity of lines of $\overrightarrow B $ , to conclude that inside a bar magnet, (a) lines of $\overrightarrow H $ run from the N-pole to S-pole, while (b) lines of $\overrightarrow B $ must run from the S-pole to N-pole.

Ans: Let PQNS be a magnet. Now consider an Amperian loop C inside and outside the magnet NS on side PQ of the magnet.

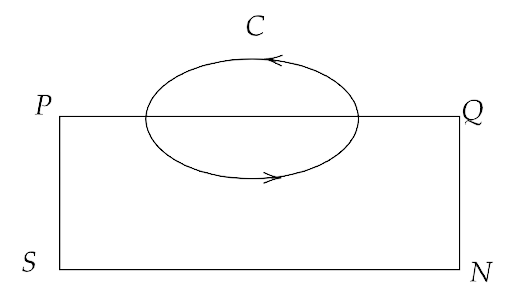
We can write, $\int\limits_P^Q {\overrightarrow H  \cdot d\overrightarrow l }  = \int\limits_Q^P {\dfrac{{\overrightarrow B }}{{{\mu _0}}} \cdot d\overrightarrow l } $

Since $\cos \theta $ is greater than 0 here, therefore $\int\limits_P^Q {\overrightarrow H  \cdot d\overrightarrow l }  = \int\limits_Q^P {\dfrac{{\overrightarrow B }}{{{\mu _0}}} \cdot d\overrightarrow l }  > 0$ i.e. positive.

Therefore, the value of the magnetic field must vary from south pole to north pole inside the magnet.

Now according to Ampere’s law, we have $\oint\limits_{PQP} {\overrightarrow H  \cdot d\overrightarrow l }  = 0$

$\oint\limits_{PQP} {\overrightarrow H  \cdot d\overrightarrow l }  = \int\limits_P^Q {\overrightarrow H  \cdot d\overrightarrow l }  + \int\limits_Q^P {\overrightarrow H  \cdot d\overrightarrow l }  = 0$

Now since $\int\limits_P^Q {\overrightarrow H  \cdot d\overrightarrow l }  > 0$ outside the magnet and $\int\limits_Q^P {\overrightarrow H  \cdot d\overrightarrow l }  < 0$ inside the magnet, it is due to the angle between H and dl which is greater than $90^\circ $ inside the magnet so $\cos \theta $ is negative. It states that the lines of H are running from north pole to south pole.

LONG ANSWER TYPE QUESTIONS

5.21 Verify the Ampere’s law for the magnetic field of a point dipole of dipole moment $\overrightarrow m  = m\widehat k$ . Take C as the closed curve running clockwise along

(i) the z-axis from z = a > 0 to z = R;

Ans: In the figure given below, every point from P to Q on the Z-axis lies on the dipole is in $\widehat k$ direction so all points on the Z-axis lie on the axial dipole NS placed at origin.

Hence, the magnetic field induction (B) at a point (0, 0, z) from the magnetic dipole having centre at origin and having a magnetic moment of magnitude $\overrightarrow m  = m\widehat k$ .

$ \Rightarrow \left| {\overrightarrow B } \right| = \dfrac{{{\mu _0}}}{{4\pi }} \cdot \dfrac{{2\overrightarrow m }}{{{z^3}}} = \dfrac{{{\mu _0}\overrightarrow m }}{{2\pi {z^3}}}$

(i) Applying the Ampere’s law along Z axis from Z=a to Z=R i.e. from P to Q, we get

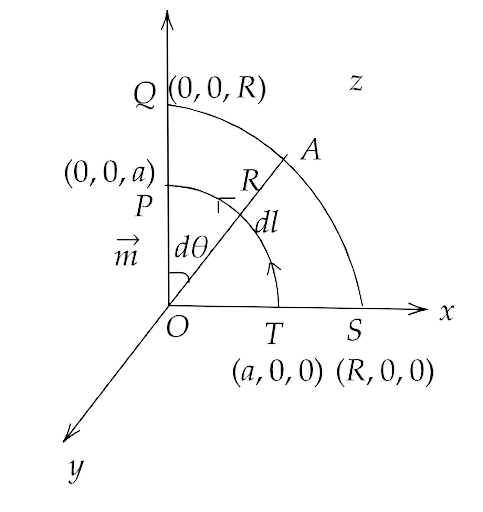
$ \Rightarrow \int\limits_P^Q {\overrightarrow B  \cdot d\overrightarrow l }  = \int\limits_P^Q {B \cdot dl\cos 0^\circ }  = \int\limits_P^Q {B \cdot dz} $

We can write it as,

$ \Rightarrow \int\limits_P^Q {\dfrac{{{\mu _0}\overrightarrow m }}{{2\pi {z^3}}} \cdot dz}  = \dfrac{{{\mu _0}\overrightarrow m }}{{2\pi }}\int\limits_a^R {{z^{ - 3}}dz} $

That gives us,

$ \Rightarrow \int\limits_P^Q {\overrightarrow B  \cdot d\overrightarrow l }  = \dfrac{{{\mu _0}\overrightarrow m }}{{4\pi }}\left[ {\dfrac{1}{{{a^2}}} - \dfrac{1}{{{R^2}}}} \right]$

(ii) along the quarter circle of radius R and centre at the origin, in the first quadrant of x-z plane;

Ans: Applying the Ampere’s law along the quarter circle of radius R and centre at the origin, in the first quadrant of x-z plane, we get

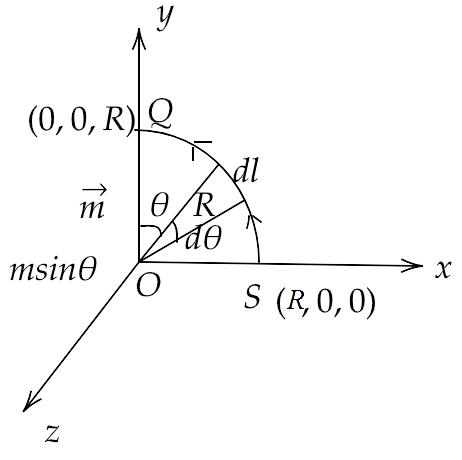
Since $B = \dfrac{{{\mu _0}}}{{4\pi }} \cdot \dfrac{{\overrightarrow m \sin \theta }}{{{R^3}}}$ and $d\theta  = \dfrac{{dl}}{R} \Rightarrow dl = Rd\theta $

Hence, 

$ \Rightarrow \int {Bdl}  = \int {Bdl} \cos \theta  = \int\limits_0^{\dfrac{\pi }{2}} {\dfrac{{{\mu _0}}}{{4\pi }} \cdot \dfrac{{\overrightarrow m \sin \theta }}{{{R^3}}}} Rd\theta $

$ \Rightarrow \int {Bdl}  = \dfrac{{{\mu _0}}}{{4\pi }} \cdot \dfrac{{\overrightarrow m }}{{{R^2}}}$

(iii) along the x-axis from x = R to x = a, and

Ans: Applying the Ampere’s law along the X axis from x = R to x=a 

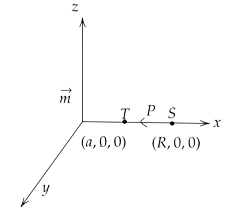
Since all the points from S to T lie on an equatorial line of magnetic dipole N-S,

Hence magnetic field induction at a point P at a distance x from the dipole is

$ \Rightarrow B = \dfrac{{{\mu _0}\overrightarrow m }}{{4\pi {x^3}}} = \dfrac{{{\mu _0}\overrightarrow m \widehat k}}{{4\pi {x^3}}}$

That gives us,

$ \Rightarrow \int {\overrightarrow B } d\overrightarrow l  = \int\limits_R^a { - \dfrac{{{\mu _0}\overrightarrow m \widehat k}}{{4\pi {x^3}}}} d\overrightarrow l $ 

Now since the angle here between dl and m is $90^\circ $ , hence

$ \Rightarrow \int {\overrightarrow B } d\overrightarrow l  =  - \int\limits_R^a {\dfrac{{{\mu _0}\left| {\overrightarrow m } \right|dl\cos 90^\circ }}{{4\pi {x^3}}}}  = 0$

(iv) along the quarter circle of radius a and centre at the origin in the first quadrant of the x-z plane.

Ans: Applying the Ampere’s law along the quarter circle of radius ‘a’ and centre at the origin in the quadrant X-Z plane, we get

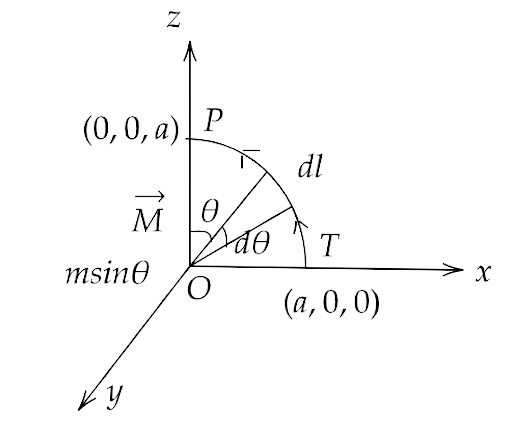
$ \Rightarrow \int {Bdl = \int\limits_{\dfrac{\pi }{2}}^0 {\dfrac{{{\mu _0}\overrightarrow m \sin \theta }}{{4\pi {a^3}}}} ad\theta } $

$ \Rightarrow \int {Bdl = \dfrac{{{\mu _0}\overrightarrow m }}{{4\pi {a^2}}}} \left[ { - \cos \theta } \right]_{\dfrac{\pi }{2}}^0$

That is,

$ \Rightarrow \int {Bdl =  - \dfrac{{{\mu _0}\overrightarrow m }}{{4\pi {a^2}}}} $

Now the sum of magnetic fields in part (i), (ii), (iii) and (iv) gives us

$ \Rightarrow \oint {Bdl = \dfrac{{{\mu _0}\overrightarrow m }}{{4\pi }}} \left( {\dfrac{1}{{{a^2}}} - \dfrac{1}{{{R^2}}}} \right) + \dfrac{{{\mu _0}\overrightarrow m }}{{4\pi {R^2}}} + 0 + \dfrac{{ - {\mu _0}\overrightarrow m }}{{4\pi {a^2}}}$

That is,

$ \Rightarrow \oint {Bdl = \dfrac{{{\mu _0}\overrightarrow m }}{{4\pi {a^2}}} - \dfrac{{{\mu _0}\overrightarrow m }}{{4\pi {R^2}}}}  + \dfrac{{{\mu _0}\overrightarrow m }}{{4\pi {R^2}}} - \dfrac{{{\mu _0}\overrightarrow m }}{{4\pi {a^2}}}$

Hence,

$ \Rightarrow \oint {Bdl = } 0$

Therefore, the Ampere’s law of magnetism is proved.

5.22 What are the dimensions of χ, the magnetic susceptibility? Consider an H-atom. Guess an expression for χ, upto a constant by constructing a quantity of dimensions of χ, out of parameters of the atom: e, m, v, R and ${\mu _0}$ . Here, m is the electronic mass, v is electronic velocity, R is Bohr’s radius. Estimate the number so obtained and compare with the value of |χ| $ \sim {10^{ - 5}}$ for many solid materials.

Ans: Since the intensity of magnetization (M) and the magnetizing field (H) both are having the same unit, therefore susceptibility, $\chi  = \dfrac{M}{H}$ has no unit and dimension. 

Now, using the Biot-Savart’s law, we have $dB = \dfrac{{{\mu _0}}}{{4\pi }} \cdot \dfrac{{Idl\sin \theta }}{{{r^2}}}$

That gives us, ${\mu _0} = \dfrac{{dB4\pi {r^2}}}{{Idl\sin \theta }}$

Now since we can write $\chi  = {\mu _0}^a{e^2}{m^b}{v^c}{R^d}$

Hence, their dimensions will be,

$ \Rightarrow \left[ {{M^0}{L^0}{T^0}{Q^0}} \right] = {\left[ {ML{Q^{ - 2}}} \right]^a}{Q^2}{M^b}{\left[ {L{T^{ - 1}}} \right]^c}{\left[ L \right]^d}$

That is,

$ \Rightarrow \left[ {{M^0}{L^0}{T^0}{Q^0}} \right] = {M^{a + b}}{L^{a + c + d}}{T^{ - c}}{Q^{ - 2a + 2}}$

That gives us, $a = 1,b =  - 1,c = 0,d =  - 1$

Therefore, we have $\chi  = {\mu _0}{e^2}{m^{ - 1}}{R^{ - 1}}$

That gives us,

$ \Rightarrow \chi  = \dfrac{{\left( {4\pi  \times {{10}^{ - 7}}} \right)\left( {1.6 \times {{10}^{ - 19}}} \right)\left( {1.6 \times {{10}^{ - 19}}} \right)}}{{\left( {9 \times {{10}^{ - 31}}} \right) \times {{10}^{ - 10}}}}$

Hence,

$ \Rightarrow \chi  = 3.5 \times {10^{ - 4}}$

Now, given that $\left| {\chi '} \right| = {10^{ - 5}}$

Hence we have

$ \Rightarrow \dfrac{\chi }{{\left| {\chi '} \right|}} = \dfrac{{3.5 \times {{10}^{ - 4}}}}{{{{10}^{ - 5}}}} = 35$

That gives, 

$ \Rightarrow \chi  = 35\left| {\chi '} \right|$

5.23 Assume the dipole model for earth’s magnetic field B which is given by vertical component of magnetic field ${B_V} = \dfrac{{{\mu _0}}}{{4\pi }} \cdot \dfrac{{2m\cos \theta }}{{{r^3}}}$ and the Horizontal component of magnetic field ${B_H} = \dfrac{{{\mu _0}}}{{4\pi }} \cdot \dfrac{{m\sin \theta }}{{{r^3}}}$ . θ = 90° latitude as measured from the magnetic equator. Find loci of points for which 

(i) |B| is minimum; 

Ans: Since the vertical and horizontal component of the magnetic field are perpendicular to each other therefore, we have ${B^2} = {B_V}^2 + {B_H}^2$

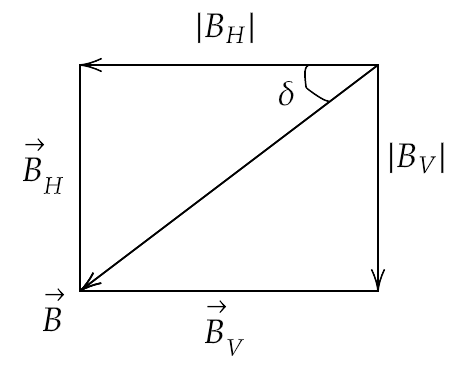
That gives us, ${B^2} = {\left( {\dfrac{{{\mu _0}}}{{4\pi }} \cdot \dfrac{{2m\cos \theta }}{{{r^3}}}} \right)^2} + {\left( {\dfrac{{{\mu _0}}}{{4\pi }} \cdot \dfrac{{m\sin \theta }}{{{r^3}}}} \right)^2}$

${B^2} = {\left[ {\dfrac{{{\mu _0}}}{{4\pi }}} \right]^2} \cdot \dfrac{{{m^2}}}{{{r^6}}}\left[ {4{{\cos }^2}\theta  + {{\sin }^2}\theta } \right]$

That is, $B = \dfrac{{{\mu _0}}}{{4\pi }} \cdot \dfrac{m}{r}{\left[ {3{{\cos }^2}\theta  + 1} \right]^{\dfrac{1}{2}}}$

Now the B will be minimum when $3{\cos ^2}\theta  + 1$ will be minimum. i.e. when $\theta  = \dfrac{\pi }{2}$ .

Hence, the magnetic equator lies at $\theta  = \dfrac{\pi }{2}$ from the magnetic dipole axis.

(ii) dip angle is zero;

Ans: Now, the angle of dip will be given by,

$ \Rightarrow \tan \delta  = \dfrac{{{B_V}}}{{{B_H}}} = \dfrac{{\dfrac{{{\mu _0}}}{{4\pi }} \cdot \dfrac{{2m\cos \theta }}{{{r^3}}}}}{{\dfrac{{{\mu _0}}}{{4\pi }} \cdot \dfrac{{m\sin \theta }}{{{r^3}}}}} = 2\cot \theta $

That gives us,

$ \Rightarrow \tan \delta  = 2\cot \dfrac{\pi }{2} = 2 \cdot 0 = 0$

Hence, $\delta  = 0^\circ $

Therefore, the angle of dip will lie at the magnetic equator.

(iii) dip angle is ± 45°.

Ans: Now if the angle of dip is given to be $ \pm 45^\circ $

Then we have, $\tan \left( { \pm 45^\circ } \right) = 1 = \dfrac{{{B_V}}}{{{B_H}}}$

Hence, ${B_V} = {B_H}$

Also, $\tan \delta  = 2\cot \theta $

So we have $\tan \left( { \pm 45^\circ } \right) = 1 = 2\cot \theta $

That gives $\tan \theta  = 2$

Hence, $\theta  = {\tan ^{ - 1}}\left( 2 \right)$ is the locus of points where the angle of dip is $ \pm 45^\circ $ .

5.24 Consider the plane S formed by the dipole axis and the axis of earth. Let P be the point on the magnetic equator and in S. Let Q be the point of intersection of the geographical and magnetic equators. Obtain the declination and dip angles at P and Q.

Ans: Let point Q be the point of intersection of the geographical meridian and the magnetic meridian.

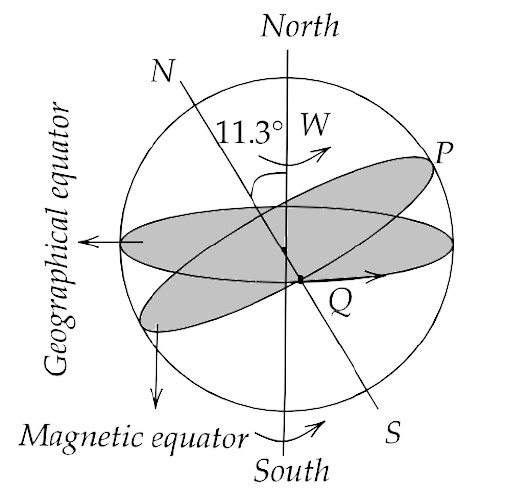
Now in that case, the angle dip at P and Q will be zero with respect to the horizontal as the magnetic middle stays horizontal.

Now since the angle between the axis of rotation of earth and the magnetic axis is $11.3^\circ $ and their respective equators are at $11.3^\circ $ with respect to their respective axis. Hence, the angle between the planes of magnetic and geographical planes will be at P and Q both.

5.25 There are two current carrying planar coils made each from identical wires of length L. ${C_1}$ is circular (radius R) and ${C_2}$ is square (side a). They are so constructed that they have the same frequency of oscillation when they are placed in the same uniform $\overrightarrow B $ and carry the same current. Find a in terms of R.

Ans: Since the frequencies for both the coils are given to be same, hence we have ${\omega _1} = {\omega _2}$

Hence we can write, $\dfrac{{2\pi }}{{{T_1}}} = \dfrac{{2\pi }}{{{T_2}}}$

${T_1} = {T_2}$

That can be written as $2\pi \sqrt {\dfrac{{{I_1}}}{{{m_1}B}}}  = 2\pi \sqrt {\dfrac{{{I_2}}}{{{m_2}B}}} $

$\sqrt {\dfrac{{{I_1}}}{{{m_1}}}}  = \sqrt {\dfrac{{{I_2}}}{{{m_2}}}} $

That gives us, $\dfrac{{{I_1}}}{{{I_2}}} = \dfrac{{{m_1}}}{{{m_2}}}$  ...(1)

Now since we have ${I_1} = \dfrac{{m{R^2}}}{2}$ and ${I_2} = \dfrac{{m{a^2}}}{{12}}$

Given that the length of wires are same and identical hence ${m_1} = {m_2} = m$

For the circular shaped coil, we have $L = 2\pi R{n_1}$

$ \Rightarrow {m_1} = {n_1}I{A_1}$

That is,

$ \Rightarrow {m_1} = \dfrac{L}{{2\pi R}}I\pi {R^2} = \dfrac{{LIR}}{2}$

For square shaped coil, we have $L = 4a{n_2}$

$ \Rightarrow {m_2} = \dfrac{L}{{4a}}I{a^2} = \dfrac{{LIa}}{4}$

Substituting all these values in equation (1) gives us,

$ \Rightarrow \dfrac{{\dfrac{{m{R^2}}}{2}}}{{\dfrac{{m{a^2}}}{{12}}}} = \dfrac{{\dfrac{{LIR}}{2}}}{{\dfrac{{LIa}}{4}}}$

That gives us,

$ \Rightarrow \dfrac{{6{R^2}}}{{{a^2}}} = \dfrac{{2R}}{a}$

$ \Rightarrow \dfrac{R}{a} = \dfrac{1}{3}$

Hence,

$ \Rightarrow a = 3R$

Important topics involved in NCERT Exemplar for Class 12 Physics Chapter 5 - Magnetism and Matter

The important topics involved in the NCERT Exemplar for Class 12 Physics Chapter 5 - Magnetism and Matter can be provided as follows:

1. Bar magnet:

The bar magnet is referred to as a piece that is rectangular in shape and made up of ferromagnetic substances. These have permanent magnetic properties and have two poles, such as the north pole and the south pole. 

2. Magnetism of Earth:

This refers to the magnetism that is produced in the earth due to the convection currents. These are formed due to the ferromagnetic substances, such as nickel or iron, present in the core of the earth. 

3. Magnetism and Gauss law:

Gauss law states that the net magnetic flux over a closed surface is zero. This law for electrostatics is much different than the magnetism gauss law. 

4. Magnetic properties of materials:

Five types of magnetic properties are discussed, such as:

• Ferromagnetic materials

• Ferrimagnetic materials

• Antiferromagnetic materials

• Diamagnetic materials

• Paramagnetic materials

Solving question papers after completing the syllabus is the best way to practice and revise at the same time. This will get you acquainted with the pattern of the question paper, the difficulty of questions, and also highlight the sections that you need to further practice. Most importantly, you’ll have to finish the paper within a stipulated time practicing this as well will ensure you have a good sense of time management for the exam.