NCERT Exemplar for Class 9 Maths - Surface Areas and Volumes - Free PDF Download

Multiple Choice Questions

Sample Question 1:  In a cylinder, if radius is halved and height is doubled, the volume will be

(A) Same

(B) Doubled

(C) Halved

(D) Four times 

Ans: Option (C) is correct.

Radius of a cylinder $= \dfrac{r}{2}$

Height of a cylinder$=2h$

Substitute the above values in the volume of a cylinder 

Volume of a cylinder $=\pi {r^2}h$ 

$V =\pi {\left( {\dfrac{r}{2}} \right)^2}\left( {2h} \right)$

$V =\pi \left( {\dfrac{{{r^2}}}{4}} \right)\left( {2h} \right)$

$V =\pi \dfrac{{{r^2}}}{2}h$

$V = \dfrac{1}{2}\pi {r^2}h$ 

Exercise 13.1

Write the correct answer in each of the following:

1. The radius of a sphere is $2r$, then its volume will be

(A) $\dfrac{4}{3}\pi {r^3}$ 

(B) $4\pi {r^3}$ 

(C) $\dfrac{{8\pi {r^3}}}{3}$

(D) $\dfrac{{32}}{3}\pi {r^3}$

Ans: Option (D) is correct.

Radius of the sphere $=2r$ 

Substitute the value in the formula.

Volume of the sphere $=\dfrac{4}{3}\pi {r^3}$

$V =\dfrac{4}{3}\pi {\left( {2r} \right)^3}$

$V =\dfrac{4}{3}\pi \left( {8{r^3}} \right)$

$V =\dfrac{{32\pi }}{3}{r^3}$

2. The total surface area of a cube is $96c{m^2}$. The volume of the cube is:

(A) $8c{m^3}$

(B) $512c{m^3}$

(C) $64c{m^3}$

(D) $27c{m^3}$

Ans: Option (C) is correct.

Total surface area of a cube $=96{\text{c}}{{\text{m}}^2}$

Total surface area of cube $=6{a^2}$ 

Substitute the total surface area value in total surface area formula.

${6{a^2}} = {96{\text{cm}}}$ 

${{a^2}} = {16{\text{c}}{{\text{m}}^2}}$ 

${a} = {\sqrt {16} }{\text{c}}{{\text{m}}^2}$

${a} = 4 {\text{c}}{{\text{m}}^2}$

Substitute the $a$  value in the volume of the cube formula.

Volume of the cube 

$\Rightarrow{a^3}$

$\Rightarrow {\left( 4 \right)^3}$

$\Rightarrow 64{\text{c}}{{\text{m}}^3}$

3. A cone is $8.4cm$ high and the radius of its base is $2.1cm$. It is melted and recast into a sphere. The radius of the sphere is :

(A) $4.2cm$

(B) $2.1cm$

(C) $2.4cm$

(D) $1.6cm$

Ans: Option (B) is correct.

Let ${r_s}$ be the radius of the sphere

Radius of the cone $=2.1{\text{cm}}$

Height of the cone $=8.4{\text{cm}}$

Volume of the cone $= $ volume of the sphere

$\Rightarrow \dfrac{1}{3}\pi r_{\text{c}}^2{\text{h}} = \dfrac{4}{3}\pi r_{\text{s}}^3$

$\Rightarrow \dfrac{1}{3}r_{\text{c}}^2{\text{h}} = \dfrac{4}{3}{\text{r}}_{\text{s}}^3$

$\Rightarrow {\text{r}}_{\text{s}}^3 = 9.261$

$\Rightarrow {{\text{r}}_{\text{s}}} = 2.1$

$\Rightarrow {{\text{r}}_{\text{s}}} = 2.1{\text{cm}}$

4. In a cylinder, radius is doubled and height is halved, curved surface area will be. 

(A) Halved

(B) Doubled

(C) Same

(D) Four times

Ans: Option (C) is correct.

Radius of a cylinder $= 2r$

Height of a cylinder $=\dfrac{h}{2}$ 

Substitute above values in curved surface area formula. 

Curved surface area of a cylinder $=2\pi rh$

$C =2\pi \left( {2r} \right)\left( {\dfrac{h}{2}} \right)$

$C = 2\pi rh$

The curved surface area will remain the same. 

5. The total surface area of a cone whose radius is $\dfrac{r}{2}$ and slant height $2l$ is

(A) $2\pi r(l + r)$ 

(B) $\pi r\left( {l + \dfrac{r}{4}} \right)$ 

(C) $\pi r(l + r)$

(D) $\quad 2\pi rl$

Ans: Option (B) is correct.

Radius $= \dfrac{r}{2}$ and slant height $= 2l$ 

Therefore,

Total surface area of cone $=\pi r\left( {l{\text{ }} + {\text{ }}r} \right)$

$\Rightarrow\pi \dfrac{r}{2}\left( {\dfrac{r}{2} + 2l} \right)$

$\Rightarrow\pi \left( {\dfrac{{{r^2}}}{4} + rl} \right)$

$\Rightarrow\pi r\left( {l + \dfrac{r}{4}} \right)$

6. The radii of two cylinders are in the ratio of $2:3$  and their heights are in the ratio of $5:3$. The ratio of their volumes is: 

(A) $10:17$

(B)$20:27$   

(C)$17:27$   

(D) $20:37$ 

Ans: Option (B) is correct.

Given the radii of two cylinders are in the ratio of $2:3$ and their heights are in the ratio of $5:3$. 

Assume the radii ${r_1}$ and ${r_2}$ be $2r$ and $3r$respectively and the height ${h_1}$ and ${h_2}$ be $5h$ and $3h$ respectively.

Therefore, the ratio of their volumes $\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{\pi {r_1}{h_1}}}{{\pi {r_2}{h_2}}}$                      

$\Rightarrow \dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{\pi {{\left( {2r} \right)}^2}\left( {5h} \right)}}{{\pi {{\left( {3r} \right)}^2}\left( {3h} \right)}}$

$\Rightarrow \dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{4\left( 5 \right)}}{{9\left( 3 \right)}}$

$\Rightarrow \dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{20}}{{27}}$

$\Rightarrow {V_1}:{V_2} = 20:27$

7. The lateral surface area of a cube is $256{m^2}$. The volume of the cube is 

(A) $512 {m^3}$ 

(B) $64 {m^3}$ 

(C) $216 {m^3}$ 

(D) $256 {m^3}$ 

Ans: Option (A) is correct.

Lateral surface area of a cube $=256{{\text{m}}^2}$

Lateral surface area of cube $=4{a^2}$ 

Substitute the lateral surface area value in lateral surface area formula.

$256{{\text{m}}^2} =4{a^2}$

$\Rightarrow{a^2} =64{{\text{m}}^{\text{2}}}$

$\Rightarrow a =8{\text{m}}$

Substitute the $a$  value in the volume of the cube formula.

Volume of the cube 

$\Rightarrow{a^3}$

$\Rightarrow {\left( 8 \right)^3}$

$\Rightarrow 512{{\text{m}}^{\text{3}}}$

8. The number of planks of dimensions ($4m \times50 cm \times20 cm$ ) that can be stored in a pit which is $16 m$ long, $12m$ wide and $4m$ deep is

(A) $1900$ 

(B)$1920$ 

(C) $1800$ 

(D) $1840$ 

Ans: Option (B) is correct.

Dimensions of the plank 

$l = 4{\text{m}}$ 

$b = 50{\text{cm}}$ 

$b = \dfrac{{50}}{{100}}{\text{m}}$ 

And $h = 20{\text{cm}}$ 

$h =0.2{\text{m}}$ 

Volume of the plank $= l \times b \times h$

$= 4 \times 0.5 \times 0.2$

$= 0.4{{\text{m}}^3}$

Dimensions of the pit are $l = 16{\text{ m}}$, $w = 12{\text{m}}$and $h = 4{\text{m}}$

Volume of the pit$= l \times b \times h$ 

$= 16 \times 12 \times 4$ 

Substitute volume of the pit and plank in the formula 

Number of planks = $\dfrac{\text{volume of the pit}}{\text{volume of the plank}}$

$= \dfrac{{16 \times 12 \times 4}}{0.4}$

$= 16 \times 12 \times 10$

$= 1920$

9. The length of the longest pole that can be put in a room of dimensions $\left( {10 m  \times  10 m  \times  5m} \right)$ is

(A) $15 m$

(B) $16 m$ 

(C) $10 m$ 

(D) $12 m$ 

Ans: Option (A) is correct.

The dimensions are $l = 10{\text{ m ,b}}{\text{ = }}10{\text{ m , h}}{\text{ = }}5{\text{m}}$ 

Diagonal of cuboid $=\sqrt {{l^2} +{b^2} +{h^2}} $ 

$= \sqrt {{{\left( {10} \right)}^2} +{{\left( {10} \right)}^2} +{{\left( 5 \right)}^2}}$

$= \sqrt {100 + 100 + 25}$

$= \sqrt {225}$

$= 15{\text{m}}$

10. The radius of a hemispherical balloon increases from $6 cm$ to $12 cm$ as air is being pumped into it. The ratios of the surface areas of the balloon in the two cases is 

(A) $1:4$ 

(B) $1:3$ 

(C) $2:3$ 

(D) $2:1$ 

Ans: Option (A) is correct.

As radius of a hemispherical balloon will be increase from $6{\text{ cm}}$ to $12{\text{ cm}}$ 

Assume the radius of a hemispherical balloon ${r_1}$ be $6{\text{ cm}}$ and as air is being pumped into it then radius of a hemispherical balloon ${r_2}$ be $12{\text{ cm}}$ 

Since ratio of the surface areas in$2$ cases $= \dfrac{{3\pi {r_1}^2}}{{3\pi {r_2}^2}}$  

$\Rightarrow \dfrac{{{r_1}^2}}{{{r_2}^2}} = \dfrac{{{{\left( 6 \right)}^2}}}{{{{\left( {12} \right)}^2}}}$

$\Rightarrow \dfrac{{{r_1}^2}}{{{r_2}^2}} = \dfrac{{36}}{{144}}$

$\Rightarrow \dfrac{{{r_1}^2}}{{{r_2}^2}} = \dfrac{1}{4}$

$\Rightarrow {r_1}:r{}_2 = 1:4$ 

Short Answer Questions with Reasoning

Sample Question 1: Write True or False and justify your answer.

A right circular cylinder just encloses a sphere of radius $r$ as shown in figure. The surface area of the sphere is equal to the curved surface area of the cylinder.

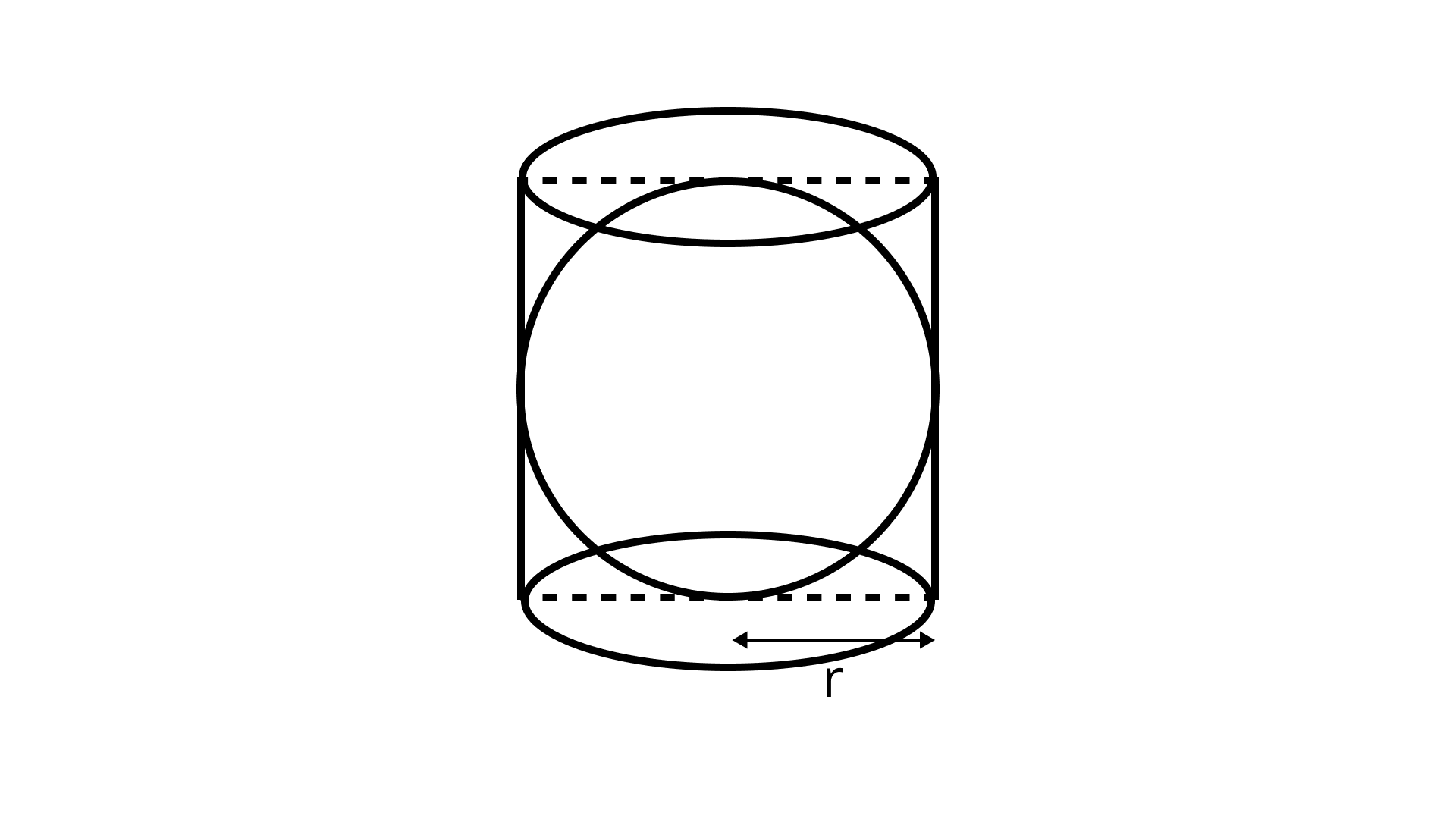
Ans: True 

Given, A right circular cylinder just encloses a sphere of radius $r$ 

i.e., radius of the sphere $= $ radius of the cylinder $= r$ 

and height of the cylinder$= $ diameter of the sphere $= 2r$ 

Since, Surface area of the sphere$= 4\pi {r^2}$ 

Curved surface area of the cylinder $= 2\pi rh$ 

Substitute height of the cylinder$ h= 2r$ in curved surface area 

Curved surface area of the cylinder $= 2\pi r\left( {2r} \right)$ 

                                                               $= 4\pi {r^2}$ 

Therefore, the surface area of the sphere is equal to the curved surface area of the cylinder.

Sample Question 2: An edge of a cube measures $r{\text{cm}}$. If the largest possible right circular cone is cut out of this cube, then the volume of the cone (in ${\text{c}}{{\text{m}}^3}$) is $\dfrac{1}{6}\pi {r^3}$.

Ans: False  

Given, edge of a cube measures $r{\text{cm}}$

The largest possible right circular cone is cut out of this cube.

Then, diameter of the cone$= r{\text{cm}}$ 

Radius of the cone $= \dfrac{r}{2}$ 

Height of the cone $= r$ 

Volume of the cone $= \dfrac{1}{3}\pi {r^2}h$ 

$= \dfrac{1}{3}\pi {\left[ {\dfrac{r}{2}} \right]^2}r$

$= \dfrac{1}{3}\pi \dfrac{{{r^2}}}{4}r$

$= \dfrac{1}{{12}}\pi {r^3}$

Exercise 13.2

Write True or False and justify your answer in each of the following:

1. The volume of a sphere is equal to two-third of the volume of a cylinder whose height and diameter are equal to the diameter of the sphere.

Ans: True

Assume the radius of the sphere $= r$ 

Given the statement, the volume of a sphere is equal to two-third of the volume of a cylinder whose height and diameter are equal to the diameter of the sphere.

Then, the radius of the cylinder $= r$

And the height of the cylinder $= 2r$

And volume of sphere $= \dfrac{2}{3}$ volume of cylinder

Since, Volume of the sphere $= \dfrac{4}{3}\pi {r^3}$ and volume of the cylinder $= \pi {r^2}h$ 

$\Rightarrow \dfrac{4}{3}\pi {r^3} = \dfrac{2}{3}\left( {\pi {r^2}\left( {2r} \right)} \right)$ because $h = 2r$

$\Rightarrow \dfrac{4}{3}\pi {r^3} = \dfrac{4}{3}\pi {r^3}$

Therefore, the volume of a sphere is up to two-thirds of the volume of a cylinder whose height and diameter are up to the diameter of the sphere.

2. If the radius of a right circular cone is halved and height is doubled, the volume will remain unchanged.

Ans: False 

Given the statement that the radius of a right circular cone is halved and height is doubled, the volume will remain unchanged is false.

The radius of a right circular cone is halved and height is doubled.

Then, the radius of the circular cone $r = \dfrac{r}{2}$ 

Height of the circular cone $h = 2h$ 

Substitute the values $r,h$ in the formula of volume of cone $= \dfrac{1}{3}\pi {r^2}h$ 

$\Rightarrow V = \dfrac{1}{3}\pi {\left( {\dfrac{r}{2}} \right)^2} \times 2h$

$\Rightarrow V = \dfrac{1}{3}\pi  \times \dfrac{{{r^2}}}{4} \times 2h$

$\Rightarrow V = \dfrac{1}{2}\left( {\dfrac{1}{3}\pi {r^2}h} \right)$

From the above relation, the radius of a right circular cone is halved and height is doubled, the volume will remain unchanged

3. In a right circular cone, height, radius, and slant height do not always be sides of a right triangle.

Ans: False 

Given statement, In a right circular cone, height, radius, and slant height do not always be sides of a right triangle is true 

Consider right circular cone

$r$ is the radius  of the cone

$h$is the height of the cone 

$l$ is slant height

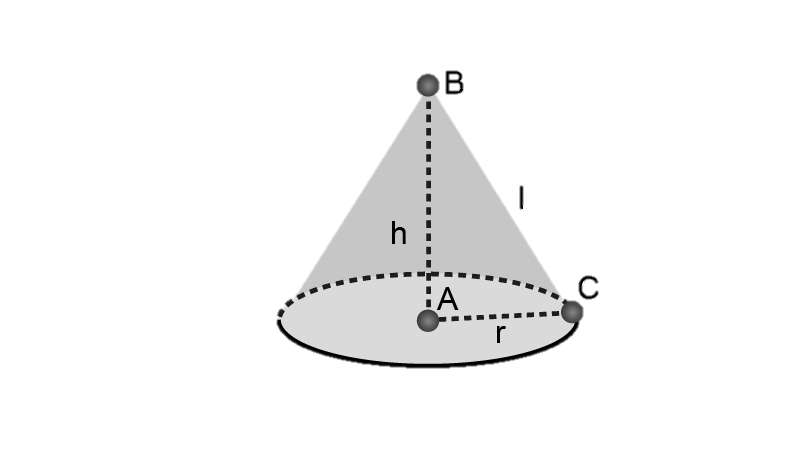
By using Pythagoras theorem 

$\Rightarrow {l^2} = {h^2} + {r^2}$ 

Therefore, the height, radius, and slant height do not always be sides of a right triangle.

4. If the radius of a cylinder is doubled and its curved surface area is not changed, the height must be halved.

Ans: True

Given, the statement If the radius of a cylinder is doubled and its curved surface area is not changed, the height must be halved is true.

From the given statement, 

Let the original dimensions of cylinder,

The radius of a cylinder is $r$ 

Height of the cylinder is $h$. 

And the new dimensions of cylinder,

Radius of a cylinder is $2r$ 

The height of the cylinder is $h'$. 

Substitute the radius and height values in the formula curved surface area of a cylinder.

The curved surface area of a cylinder $= 2\pi rh$ 

$\Rightarrow 2\pi rh = 2\pi (2r) \times h'$

$\Rightarrow \quad 2\pi rh = 4\pi rh'$

$\Rightarrow h' = \dfrac{{2\pi rh}}{{4\pi r}}$

$\Rightarrow h' = \dfrac{h}{2}$

Therefore, the height must be halved.

5. The volume of the largest right circular cone can be fitted in a cube whose edge is $2r$ equals to the volume of a hemisphere of radius $r$. 

Ans: True

Given, the statement the volume of the largest right circular cone that can be fitted in a cube whose edge is $2r$ equals to the volume of a hemisphere of radius $r$is true 

Given, 

Edge of cube is $2r$, then height of the cube $h = 2r$. 

The volume of a cone $= \dfrac{1}{3}\pi {r^2}h$

$V = \dfrac{1}{3}\pi {r^2}(2r)$

$V = \dfrac{2}{3}\pi {r^3}$

Volume of a cone $= $ Volume of a hemisphere of radius $r$ 

6. A cylinder and a right circular cone are having the same base and same height. The volume of the cylinder is three times the volume of the cone.

Ans: True

Given the statement, a cylinder and a right circular cone are having the same base and same height. The volume of the cylinder is three times the volume of the cone is true.

Assume the radius of the base of a cylinder and a right circular cone be $r$ 

and height is $h$. 

Since, Volume of a cylinder $= \pi {r^2}h$

Volume of a cone $= \dfrac{1}{3}\pi {r^2}h$

Then, 

Volume of a cylinder $= 3 \times $ Volume of a cone

From the above relation, the volume of the cylinder is 3 times of the volume of a cone

7. A cone, a hemisphere and a cylinder stand on equal bases and have the same height. The ratio of their volumes is $1:2:3$.

Ans: True

Given the statement is a cone, a hemisphere and a cylinder stand on equal bases and have the same height. The ratio of their volumes is $1:2:3$ is true.

Since, volume of the cylinder is $\pi {r^2}h$ 

Volume of the hemisphere is $\dfrac{2}{3}\pi {r^3}$ 

Volume of the cone is $\dfrac{1}{3}\pi {r^2}h$ 

The ratio of a cone, hemisphere and a cylinder is ${V_c}:{V_h}:{V_{cyl}}$

$\Rightarrow \dfrac{1}{3}\pi {r^2}h:\dfrac{2}{3}\pi {r^3}:\pi {r^2}h$

$\Rightarrow \dfrac{1}{3}\pi {r^3}:\dfrac{2}{3}\pi {r^3}:\pi {r^3}$

$\Rightarrow \pi {r^3}:2\pi {r^3}:3\pi {r^3}$

$\Rightarrow 1:2:3$ 

Therefore, The ratio of a cone, hemisphere and a cylinder is $1:2:3$

8. If the length of the diagonal of a cube is $6\sqrt 3  cm$, then the length of the edge of the cube is $3 cm$. 

Ans: False 

Given the statement, If the length of the diagonal of a cube is $6\sqrt 3 {\text{ cm}}$, then the length of the edge of the cube is $3{\text{ cm}}$ is false

Given, the length of the diagonal of a cube $= 6\sqrt 3 {\text{cm}}$

Let the edge of a cube be $a{\text{ cm}}$.

Since, diagonal of a cube $= {\text{a}}\sqrt 3 $

On comparing 

$\Rightarrow 6\sqrt 3  = a\sqrt 3 $

$\Rightarrow a = 6{\text{cm}}$

Therefore, the edge of a cube is $6{\text{cm}}$.

9. If a sphere is inscribed in a cube, then the ratio of the volume of the cube to the volume of the sphere will be $6:\pi $

Ans: True 

Given the statement that if a sphere is inscribed in a cube, then the ratio of the volume of the cube to the volume of the sphere will be $6:\pi $ is true.

Given a sphere is inscribed in a cube

Calculate the ratio between the volume of a sphere and a volume of a cube 

Since, the diameter of the sphere is equal to the side of the cube.

Let the diameter of the sphere be $d$ 

Then, radius be $\dfrac{d}{2}$ 

Substitute the radius value in volume of a sphere.   

Volume of a sphere $\left( {{V_s}} \right) = \left( {\dfrac{4}{3}} \right)\pi {\left( {\dfrac{d}{2}} \right)^3}$

${V_s} = \left( {\dfrac{4}{3}} \right)\pi \left( {\dfrac{{{d^3}}}{8}} \right)$

${V_s} = \dfrac{{\pi {d^3}}}{6}$

Volume of a cube $\left( {{V_c}} \right) = {s^3}$

${V_c} = {d^3}$

Then, the ratio between the volume of a sphere and a volume of a cube $= \dfrac{{{V_s}}}{{{V_c}}}$ 

$\Rightarrow \dfrac{{{V_s}}}{{{V_c}}} = \dfrac{{\left( {\dfrac{{\pi {d^3}}}{6}} \right)}}{{{d^3}}}$

Therefore, the ratio of the volume of the cube to the volume of sphere is $6:\pi $.

10. If the radius of a cylinder is doubled and height is halved, the volume will be doubled.

Ans: True

Given the statement, if the radius of a cylinder is doubled and height is halved, the volume will be doubled is true. 

Let the radius of a cylinder $R = 2r$ 

And height of a cylinder, $h = \dfrac{h}{2}$ 

Then substitute the values in volume of cylinder $V = \pi {r^2}h$ 

 Volume of cylinder $V = \pi {(2r)^2}\dfrac{h}{2}$

$V = 2\pi {r^2}h$

Therefore, if the radius of a cylinder is doubled and height of a cylinder is halved, then volume of the cylinder is doubled.

Short Answer Questions

Sample Question 1: The surface area of a sphere of radius $5 cm$ is five times the area of the curved surface of a cone of radius $4 cm$. Find the height and the volume of the cone (taking $\pi = \dfrac{{22}}{7}$ ).

Ans: Given the surface area of a sphere of radius $5{\text{ cm}}$ is five times the area of the curved surface of a cone of radius $4{\text{ cm}}$. 

i.e.., surface area of a sphere $= 5$(curved surface of a cone)

$4\pi {r^2}$= $5\left( {\pi rl} \right)$

Substitute the values of  radius in above formula 

$\Rightarrow 4 \times 25 = 5\left( {4 \times l} \right)$ 

$\Rightarrow 20 = 4l$

$\Rightarrow l = 5{\text{cm}}$

Calculate height of the cone by using the formula ${h^2} = {l^2} - {r^2}$ 

$\Rightarrow {h^2} = {\left( 5 \right)^2} - {\left( 4 \right)^2}$

$\Rightarrow {h^2} = 25 - 16$

$\Rightarrow {h^2} = 9$

$\Rightarrow h = 3$

Now, calculate the volume of the cone by using $V = \dfrac{1}{3}\pi {r^2}h$

$\Rightarrow V = \dfrac{1}{3} \times \dfrac{{22}}{7} \times {\left( 4 \right)^2} \times3$

$\Rightarrow V = \dfrac{{352}}{7}$

$\Rightarrow V = 50.29{\text{c}}{{\text{m}}^{\text{2}}}$

Sample Question 2: The radius of a sphere is increased by $10\% $. Prove that the volume will be increased by $33.1\% $ approximately.

Ans: Given the radius of a sphere is increased by $10\% $. 

$10\% {\text{ increase in radius}}{\text{ = }}10\%r{\text{ }}$

$\Rightarrow {\text{Increased radius}} =r +\dfrac{1}{{10}}r$

$\Rightarrow {\text{Increased radius}} = \dfrac{{11}}{{10}}r$

Substitute the value of increased radius in formula volume of sphere

Volume of a sphere $= \dfrac{4}{3}\pi {r^3}$ 

$V = \dfrac{4}{3}\pi {\left( {\dfrac{{11}}{{10}}r} \right)^3}$

$V = \dfrac{4}{3}\pi  \times \dfrac{{1331}}{{1000}}{r^3}$

$V = \dfrac{4}{3}\pi  \times 1.331{r^3}$

Difference increased volume and original volume is.

$= \dfrac{4}{3}\pi {R^3}(1.331) - \dfrac{4}{3}\pi {R^3}$

$= \dfrac{4}{3}\pi {R^3}(1.331 - 1)$

$= \dfrac{4}{3}\pi {R^3}(0.331)$

The volume will be increased $\% $is 

Increase $\% $ $= \dfrac{{\dfrac{4}{3}\pi {R^3}(0.331)}}{{\dfrac{4}{3}\pi {R^3}}} \times 100$

Increase % $= 33.1\% $

Exercise 13.3

1. Metal spheres, each of radius $2cm$, are packed into a rectangular box of internal dimensions $16 cm  \times  8 cm  \times  8 cm$. When $16$ spheres are packed the box is filled with preservative liquid. Find the volume of this liquid. Give your answer to the nearest integer. Use $\pi  = 3.14$

Ans: Given,

Metal sphere of each radius $= 2{\text{cm}}$

And internal dimension of a packed rectangular box is  $l = 16{\text{cm}},b = 8{\text{cm}}$and $h = 8{\text{cm}}$

Calculate the volume of a metal sphere

Volume of a  sphere $= \dfrac{4}{3}\pi {r^3}$

$= \dfrac{4}{3} \times 3.14 \times {(2)^3}$

$= \dfrac{4}{3} \times 3.14 \times 8$

Now, calculate the volume for $16$metal spheres 

Volume of $16$ metal spheres $= 16 \times \dfrac{{4 \times 3.14 \times 8}}{3}$

$\Rightarrow \dfrac{{100.48 \times 16}}{3}$

$\Rightarrow \dfrac{{1607.68}}{3}$

$\Rightarrow 535.89{\text{c}}{{\text{m}}^3}$

Calculate the internal volume of a rectangular box 

$V = l \times b \times h$

$V = 16 \times 8 \times 8$

$V = 1024{\text{c}}{{\text{m}}^3}$

When $16$ spheres are packed in the rectangular box is filled with preservative liquid

Calculate the volume of preservative liquid 

${V_l} = 1024 - 535.89$ 

${V_l} = 488.11$

${V_l} \approx 488{\text{c}}{{\text{m}}^3}$

2. A storage tank is in the form of a cube. When it is full of water, the volume of water is $15.625 {m^3}$.If the present depth of water is $1.3 m$, find the volume of water already used from the tank.

Ans: Given, a storage tank is in the form of a cube

When the tank is full of water then volume of water is $15.625{\text{ }}{{\text{m}}^3}$

So that Volume of water will be equal to the Volume of cube 

Volume of a cube $= 15.625{\text{ }}{{\text{m}}^3}$

Volume of a cube$= {a^3}$ 

$15.625{\text{ }}{{\text{m}}^3} = {a^3}$

$a = \sqrt[3]{{15.625{\text{ }}{{\text{m}}^3}}}$ 

$a = 2.5{\text{m}}$ 

Length of the edge of the cube $= 2.5{\text{m}}$ 

If the present depth of the water is $1.3{\text{ m}}$i.e., $d =2.5{\text{ m}}$ 

Then, Length of tank $l = 2.5{\text{ m}}$ 

Breadth of tank $b = 2.5{\text{ m}}$ 

Volume of water $1.3{\text{ m}}$ depth 

${V_{1.3}} = l \times b \times h$ 

${V_{1.3}} = 2.5 \times2.5 \times1.3$ 

${V_{1.3}} = 8.125{\text{ }}{{\text{m}}^3}$ 

Then, to calculate the volume of water already used from the tank

Volume of water already used from the tank

$= $  (Volume of tank when it was full of water)  $ - $  (Volume of water when depth is $1.3{\text{ m}}$ ) 

Volume of water already used from the tank$= 15.625-8.125$   

Volume of water already used from the tank$= 7.5{\text{ }}{{\text{m}}^3}$ 

3. Find the amount of water displaced by a solid spherical ball of diameter $4.2{\text{ cm}}$, when it is completely immersed in water

Ans: Given, 

Diameter of a spherical ball is $4.2{\text{ cm}}$

Then radius is $\dfrac{d}{2}$ 

 $\Rightarrow r = \dfrac{{4.2}}{2}$

 $\Rightarrow r = 2.1{\text{cm}}$ 

From the given question, 

When a solid spherical ball is immersed completely in water it will be equal to the volume of the sphere.  

Since, volume of the sphere $V = \dfrac{4}{3}\pi {r^3}$ 

$\Rightarrow V = \dfrac{4}{3} \times \dfrac{{22}}{7} \times {\left( {21} \right)^3}$

$V = \dfrac{{814.968}}{{21}}$

$V\approx 38.81{\text{c}}{{\text{m}}^3}$

4. How many square meters of canvas is required for a conical tent whose height is$3.5 m$ and the radius of the base is $12 m$? 

Ans: Given, 

Height of the conical tent is $3.5{\text{ m}}$

Radius of the base is $12{\text{ m}}$

Calculate the slant height of conical test by using the formula $l = \sqrt {{h^2} + {r^2}} $ 

$\Rightarrow l = \sqrt {{{\left( {3.5} \right)}^2} + {{\left( {12} \right)}^2}} $ 

$\Rightarrow l = \sqrt {12.25 + 144}$

$\Rightarrow l = \sqrt {156.25}$

$\Rightarrow l = 12.5{\text{m}}$

Canvas required for a conical tent is equal to the volume of a cone 

Volume of the cone $= \pi rl$ 

$V = \dfrac{{22}}{7} \times 12 \times 12.5$

$V = 471.42{{\text{m}}^2}$

5. Two solid spheres made of the same metal have weights $5920{\text{ g}}$and $740{\text{ g}}$, respectively. Determine the radius of the larger sphere, if the diameter of the smaller one is $5{\text{ cm}}$.

Ans: Given, Weights of the two solid spheres ${w_1}$ and ${w_2}$are $5920{\text{ g}}$ and $740{\text{ g}}$ respectively 

Diameter of the smaller solid sphere is ${d_2} = 5{\text{cm}}$ 

Radius of the smaller solid sphere is ${r_2} = \dfrac{{{d_2}}}{2}$ 

$\Rightarrow {r_2} = \dfrac{5}{2}{\text{cm}}$ 

Now, calculate the volume of the each sphere by using 

$V = \dfrac{{{\text{mass}}}}{{{\text{density}}}}$ 

Volume of the larger sphere${V_1} = \dfrac{{5920}}{D}$ 

$\Rightarrow \dfrac{4}{3}\pi {r_1}^3 = \dfrac{{5920}}{D}$ 

Volume of the smaller sphere${V_2} = \dfrac{{740}}{D}$ 

$\Rightarrow \dfrac{4}{3}\pi {r_2}^3 = \dfrac{{740}}{D}$

Calculate the ratios of volumes of solid sphere $\dfrac{{{V_1}}}{{{V_2}}}$ to find radius of the larger sphere 

$\Rightarrow \dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{\dfrac{{5920}}{D}}}{{\dfrac{{740}}{D}}}$

$\Rightarrow \dfrac{{\dfrac{4}{3}\pi {r_1}^2}}{{\dfrac{4}{3}\pi {r_2}^2}} = \dfrac{{5920}}{{740}}$

$\Rightarrow \dfrac{{{r_1}^2}}{{{{\left( {\dfrac{5}{2}} \right)}^2}}} = \dfrac{{592}}{{74}}$ 

$\Rightarrow \dfrac{{\dfrac{{{r^3}}}{{125}}}}{8} = \dfrac{{592}}{{74}}$

$\Rightarrow \dfrac{{8{r^3}}}{{125}} = \dfrac{{592}}{{74}}$

$\Rightarrow r_1^3 = \dfrac{{592}}{{74}} \times \dfrac{{125}}{8}$

$\Rightarrow r_1^3 = \dfrac{{74000}}{{592}}$

$\Rightarrow r_1^3 = 125$

$\Rightarrow {r_1} = \sqrt[3]{{125}}$

$\Rightarrow {r_1} = 5{\text{cm}}$

6. A school provides milk to the students daily in a cylindrical glasses of diameter $7cm$. If the glass is filled with milk upto a height of $12cm$, find how many litres of milk is needed to serve $1600$  students.

Ans: Given 

Diameter of cylinder $d = 7{\text{cm}}$Then, Radius of cylinder, $r = \dfrac{d}{2}$

$r = \dfrac{7}{2}$

$r = 3.5{\text{cm}}$  

The glass is filled with milk upto a height, $h = 12{\text{cm}}$

Then, volume of milk in cylindrical glass is equal to the volume of the cylinder

Volume of the cylinder $V = \pi {r^2}h$

$\Rightarrow V = \dfrac{{22}}{7} \times 3.5 \times 3.5 \times 12$

$\Rightarrow V = 462{\text{c}}{{\text{m}}^3}$

For $1600$ students, the volume of the milk is 

$V = 1600 \times 462{\text{c}}{{\text{m}}^3}$

$V = 739200{\text{c}}{{\text{m}}^3}$

$1$ liter $= 1000{\text{c}}{{\text{m}}^3}$ 

i.e., $1{\text{c}}{{\text{m}}^3} = 0.001$ liters

Then, Volume of milk for $1600$ students 

$V = 739200 \times 0.001$

$V = 739.2{\text{liters}}$

7. A cylindrical roller $2.5m$ in length, $1.75m$ in radius when rolled on a road was found to cover the area of $5500{m^2}$. How many revolutions did it make?

Ans: Given,

Length of cylindrical roller that is equal to height of the cylinder

$h = 2.5{\text{m}}$

Radius of cylindrical roller, $r = 1.75{\text{m}}$

When rolled on a road was found to cover the area of $5500{{\text{m}}^2}$. 

Curved surface area of cylindrical roller is equal to the volume of the cylinder

$CSA = 2\pi rh$

Substitute the values in the formula of curved surface area

$\Rightarrow CSA = 2 \times \dfrac{{22}}{7} \times 1.75 \times 2.5$

$\Rightarrow CSA = 27.5{{\text{m}}^2}$

Area of road covered in one revolution $= 27.5{{\text{m}}^2}$

According to the question, total area of road covered $= 5500{{\text{m}}^2}$

So that, number of revolutions made by road roller to cover $5500{{\text{m}}^2}$ 

${\text{number }}{\text{of }}{\text{revolutions}} = \dfrac{{5500}}{{27.5}}$

${\text{number} }{\text{of }}{\text{revolutions}} = 200$

8. A small village, having a population of $5000$, requires $75$litres of water per head per day. The village has got an overhead tank of measurement $40m \times 25m \times 15m$. For how many days will the water of this tank last?

Ans: Given, 

A small village having a population$= 5000$

Water required per head per day $= 75{\text{L}}$ 

Determine the volume of water required for a small village per day 

${V_w} = 5000 \times 75$

${V_w} = 375000{\text{L}}$

Since, $1{{\text{m}}^3}$ equal to $1000{\text{L}}$

${V_w} = \dfrac{{375000}}{{1000}}{{\text{m}}^3}$

${V_w} = 375{{\text{m}}^3}$

Total capacity of water in overhead tank will be equal to Volume of overhead tank

${V_t} = 40 \times 25 \times 15$

${V_t} = 15000{{\text{m}}^3}$

To find number of days will the water of this tank last is 

${\text{ Number of days}} = \dfrac{{{V_t}}}{{{V_w}}}$

${\text{Number of days}} = \dfrac{{15000}}{{375}}$

${\text{Number of days}} = 40{\text{ days}}$

9. A shopkeeper has one spherical laddoo of radius $5cm$. With the same amount of material, how many laddoos of radius $2.5cm$ can be made?

Ans: Given the spherical laddoo of a radius $r = 5{\text{cm}}$

Volume of spherical laddoo will be equal to the volume of the sphere 

Since,  $V = \dfrac{4}{3}\pi {r^3}$

$\Rightarrow {V_5} = \dfrac{4}{3} \times \dfrac{{22}}{7} \times 5 \times 5 \times 5$

$\Rightarrow {V_5} = 523.81$

With the same amount of material number of laddoos with radius $2.5{\text{cm}}$ can be made.

Volume of laddoo having the radius $2.5{\text{cm}}$

${V_{2.5}} = \dfrac{4}{3} \times \dfrac{{22}}{7} \times 2.5 \times 2.5 \times 2.5$

${V_{2.5}} = 65.48{\text{c}}{{\text{m}}^3}$

Therefore, laddoos with radius $2.5{\text{cm}}$ can be made is 

Number of laddoos $= \dfrac{{523.81}}{{65.48}}$

Number of laddoos $= 8$

10. A right triangle with sides $6cm,8cm$ and $10cm$ is revolved about the side $8cm$. Find the volume and the curved surface of the solid so formed.

Ans: Given

A right triangle with sides $6{\text{cm}},8{\text{cm}}$ and $10{\text{cm}}$ is revolved about the side 8 ${\text{cm}}$

Radius of a cone, $r = 6{\text{cm}}$ 

Height of a cone, $h = 8{\text{cm}}$ 

Slant height of a cone, $l = 10{\text{cm}}$ 

Since, Volume of a cone ,$V = \dfrac{1}{3}\pi {r^2}h$

$V = \dfrac{1}{3} \times \dfrac{{22}}{7} \times 6 \times 6 \times 8$

$V = \dfrac{6336}{21}$

$V = 301.7{\text{c}}{{\text{m}}^3}$

Now, calculate the curved surface of the area of cone

$CSA = \pi rl$

$CSA = \dfrac{{22}}{7} \times 6 \times 10$

$CSA =\dfrac{ 1320}{7}$

$CSA = 188.5{\text{c}}{{\text{m}}^2}$ 

Long Answer Questions

Sample Question 1: Rain water which falls on a flat rectangular surface of length $6 m$ and breadth $4 m$ is transferred into a cylindrical vessel of internal radius $20 cm$. What will be the height of water in the cylindrical vessel if the rain fall is $1 cm$. Give your answer to the nearest integer. (Take $\pi  = 3.14$)

Ans: Given 

Length of the cuboid $= 600{\text{cm}}$ 

Breadth of the cuboid $= 400{\text{cm}}$ 

Since, the rainfall is $1{\text{cm}}$. 

The quantity of Rainwater that falls on a flat rectangular surface will be $600{\text{ cm}}$ ,$400{\text{ cm}}$ by $1{\text{ cm}}$. 

The quantity of water that accumulates on a rectangular surface will be the volume of a cuboid 

Volume of a cuboid $= l \times b \times h$ 

Substituting values in the volume of the cuboid formula 

$V = l \times b \times h$

$V = 600 \times 400 \times 1$ 

The volume of water on rectangular surface $= 240000{\text{c}}{{\text{m}}^{\text{3}}}$ 

Since this water on a rectangular surface is transferred to a cylindrical vessel. 

Therefore, the quantity of Rainwater that falls on a flat rectangular surface unit gets to be up to the quantity of water entering into the cylindrical vessel. 

Assume the height of the cylindrical vessel be $h$. 

Volume of cylinder $= \pi {r^2}h$ 

Substituting values in the volume of a cylinder 

$\Rightarrow 240000 = \pi  \times {\left( {20} \right)^2} \times h$ 

$\Rightarrow h = \dfrac{{240000}}{{\pi  \times 20 \times 20}}$ 

$\Rightarrow h = \dfrac{{600}}{{3.14}}$ 

$\Rightarrow h = 191{\text{cm}}$ 

Exercise 13.4

1. A cylindrical tube opened at both the ends is made of iron sheet which is $2{\text{ cm}}$ thick. If the outer diameter is $16{\text{ cm}}$ and its length is $100{\text{ cm}}$, find how many cubic centimeters of iron has been used in making the tube ?

Ans: Given,

Length of the cylinder is also equal to the height of the cylinder 

So, Height $= 100{\text{cm}}$

Length $= 100{\text{cm}}$

Outer diameter $d = 16{\text{cm}}$

Then, outer radius will be 

$r = \dfrac{{16}}{2}$

$r = 8{\text{cm}}$

Since, volume of outer cylinder $= \pi {r^2}h$ 

${V_O} = \pi {\left( 8 \right)^2}\left( {100} \right)$

${V_O} = \dfrac{{22}}{7}\left( {64} \right)\left( {100} \right)$

${V_O} = 20096{\text{c}}{{\text{m}}^2}$

From the question, cylindrical tube opened at both the ends is made of iron sheet which is $2{\text{ cm}}$ thick

So that thickness of iron sheet $= 2{\text{cm}}$

Then, inner diameter $= $ outer diameter $ -2\left( {{\text{thickness of iron sheet}}} \right)$ 

Inner diameter $= 16 - (2 \times 2)$

Inner diameter $= 12{\text{cm}}$

Therefore, Inner radius $(R) = \dfrac{{12}}{2} = 6{\text{cm}}$

Volume of inner cylinder $= \pi {R^2}h$ 

Where 

${\text{R}} = $ inner radius

${V_I} = \pi {R^2}h$

${V_I} = \dfrac{{22}}{7} \times {(6)^2} \times 100$

${V_I} = 11304{\text{c}}{{\text{m}}^3}$

Since, Volume of iron used$= $Volume of outer cylinder$ - $Volume of inner cylinder

$V = {V_O} - {V_I}$

$V = 20096 - 11304$

$V = 8792{\text{c}}{{\text{m}}^3}$

2.  A semi-circular sheet of metal of diameter $28cm$ is bent to form an open conical cup. Find the capacity of the cup.

Ans: Diameter of the circular sheet $= 28{\text{cm}}$.

Radius of the circular sheet $= 14{\text{cm}}$. 

Circumference of semi circular sheet$= 14\pi $.

Now the semicircular sheet is bent into an open conical cup. 

Slant height of conical cup $\left( l \right)$ will be radius of circular sheet 

So that, $l = 14{\text{cm}}$ 

Circumference of the base of conical cup will be circumference of semicircular sheet 

$2\pi R = 14\pi $

$R = 7{\text{cm}}$

Depth of conical cup will be height of cone

$h = \sqrt {{l^2} - {r^2}}$

$h = \sqrt {{{(14)}^2} - {{(7)}^2}}$

$h = \sqrt {196 - 49}$

$h = \sqrt {147}$

$ h = 7\sqrt 3 {\text{cm}}$

Capacity of conical cup will be Volume of cone

$V = \dfrac{1}{3}\pi {R^2}h$

$V = \dfrac{1}{3} \times \dfrac{{22}}{7} \times {7^2} \times 7\sqrt 3$

$V = \dfrac{{1078\sqrt 3 }}{3}{\text{c}}{{\text{m}}^3}$ 

3. A cloth having an area of $165{m^2}$ is shaped into the form of a conical tent of radius $5m$

(i) How many students can sit in the tent if a student, on an average, occupies $\dfrac{5}{7}{{\text{m}}^2}$ on the ground?

Ans: Given 

Curved Surface Area of the cone is$165{{\text{m}}^2}$ 

Radius of tent is$5{\text{m}}$ 

Space occupied by each candidate is$\dfrac{5}{7}{{\text{m}}^2}$

Calculate the number of candidates can sit on the ground

Number of candidates can sit on the ground $= $ Curved Surface Area of the base $ \div $ space occupied by each candidate

$= \pi {r^2} \div \dfrac{5}{7}$ 

$= \dfrac{{22}}{7} \times 25 \times \dfrac{7}{5}$

$= 110$

(ii) Find the volume of the cone.

Ans: To find the volume of the cone first calculate the slant height of the cone.

Since, CSA of cone $= 165{{\text{m}}^2}\quad $ 

Radius of tent is $5{\text{m}}$ 

Curved Surface Area$= \pi rl$ 

$l$ is slant height    

Slant height $= \sqrt {{r^2} + {h^2}} $

$165 = \dfrac{{22}}{7} \times 5 \times \sqrt {25 + {h^2}} $ 

$10.5 = \sqrt {25 + {h^2}} $

$110.25 = {h^2} + 25$ 

squaring on both the sides 

${h^2} = 110.25 - 25$

$ {h^2} = 85.25$ 

$h = 9.23{\text{m}}$

Now, Volume of cone $= \dfrac{1}{3}\pi {r^2}h$

$V = \dfrac{1}{3} \times \dfrac{{22}}{7} \times 25 \times 9.23$

$V = 241.74{{\text{m}}^3}$ 

4. The water for a factory is stored in a hemispherical tank whose internal diameter is $14 m$. The tank contains $50$ kilolitres of water. Water is pumped into the tank to fill its capacity. Calculate the volume of water pumped into the tank.

Ans: Given, 

Internal diameter $= 14{\text{m}}$ 

Thus, radius $r = \dfrac{{14}}{2}$ 

$\Rightarrow r = 7{\text{cm}}$ 

Capacity of the tank will be volume of the hemisphere

Volume of the hemisphere $= \dfrac{2}{3}\pi {r^3}$ 

$\Rightarrow V = \dfrac{2}{3}\pi {\left( 7 \right)^3}$

$\Rightarrow V = \dfrac{2}{3} \times \dfrac{{22}}{7}\left( {343} \right)$

$\Rightarrow V = 718.67{\text{c}}{{\text{m}}^3}$

We know that 50 kilolitres = $50 {m^3}$

Volume of water pumped into the tank $= $ Capacity of the tank $ -50$ 

$= 718.67 - 50$

$= 668.66{\text{ }}{{\text{m}}^{\text{3}}}$

5. The volumes of the two spheres are in the ratio $64:27$. Find the ratio of their surface areas.

Ans: Given, the ratio of volume of the two spheres are $64:27$

Assume the radius of two spheres are ${r_1}$ and ${r_2}$ respectively.

Therefore, 

Volume of the sphere of radius ${r_1}$ 

${V_1} = \dfrac{4}{3}\pi r_1^3$

and volume of the sphere of radius${r_2}$ 

${V_2} = \dfrac{4}{3}\pi r_2^3$

Calculate the radius by using the ratio of volume of the two spheres 

${V_1}:{V_2} = \dfrac{{64}}{{27}}$

$\Rightarrow {V_1}:{V_2} = \dfrac{{\dfrac{4}{3}\pi r_1^3}}{{\dfrac{4}{3}\pi r_2^3}}$

$\Rightarrow \dfrac{{\dfrac{4}{3}\pi r_1^3}}{{\dfrac{4}{3}\pi r_2^3}} = \dfrac{{64}}{{27}}$

$\Rightarrow \dfrac{{r_1^3}}{{r_2^3}} = \dfrac{{64}}{{27}}$

$\Rightarrow \dfrac{{{r_1}}}{{{r_2}}} = \dfrac{4}{3}$

$\Rightarrow {r_1}:{r_2} = 4:3$ 

From the radius calculate the ratios of the surface area of a sphere

Now, ratios of surface area $\dfrac{{{s_1}}}{{{s_2}}}$  $= \dfrac{{4\pi r_1^2}}{{4\pi {r_2^2}}}$ 

$\dfrac{{{s_1}}}{{{s_2}}} = {\left( {\dfrac{{{r_1}}}{{{r_2}}}} \right)^2}$

$\dfrac{{{s_1}}}{{{s_2}}} = {\left( {\dfrac{4}{3}} \right)^2}$

$\dfrac{{{s_1}}}{{{s_2}}} = \dfrac{{16}}{9}$ 

$\Rightarrow {s_1}:{s_2} = 16:9$ 

6. A cube of side $4 cm$ contains a sphere touching its sides. Find the volume of the gap in between.

Ans: Given, 

 Side of a cube $\left( a \right) = 4{\text{cm}}$

Calculate the volume of the cube 

Volume of cube is $V = {a^3}$ 

$V = {(4{\text{cm}})^3}$

$V = 64{\text{c}}{{\text{m}}^3}$

Diameter of the sphere will be equal to length of the side of the cube 

Side of the cube $= 4{\text{cm}}$

Diameter of the sphere$= 4{\text{cm}}$ 

Then, Radius of sphere $= 2{\text{cm}}$

Volume of the sphere $= \dfrac{4}{3}\pi {r^3}$ 

$V = \dfrac{4}{3} \times \dfrac{{22}}{7} \times {(2)^3}$

$V = 33 \cdot 52{\text{c}}{{\text{m}}^3}$

Therefore,  Volume of gap$= $  Volume of a cube$ - $ Volume of sphere 

$V = 64{\text{c}}{{\text{m}}^2} - 33 \cdot 52{\text{c}}{{\text{m}}^3}$

$V = 30 \cdot 48{\text{c}}{{\text{m}}^3}$

7. A sphere and a right circular cylinder of the same radius have equal volumes. By what percentage does the diameter of the cylinder exceed its height ?

Ans: Assume that radius of sphere and radius of a right circular cylinder is $r$ and height of the cylinder be $h$ 

From the given question, sphere and a right circular cylinder of the same radius have equal volumes

Since, Volume of cylinder $= $ volume of a sphere 

Volume of sphere $= \dfrac{4}{3}\pi {r^3}$

Volume of cylinder $= \pi {r^2}h$ 

$\Rightarrow \pi {r^2}h = \dfrac{4}{3}\pi {r^3}$

$\Rightarrow h = \dfrac{4}{3}r$

Since, Diameter of the cylinder $d = 2{\text{r}}$

$\Rightarrow h = \dfrac{{2\left( {2r} \right)}}{3}$ 

$\Rightarrow h = \dfrac{{2d}}{3}$

$\Rightarrow 3h = 2d$

$\Rightarrow d = \dfrac{{3h}}{2}$

The difference between the length of diameter and height is $d - h$ 

$\Rightarrow \dfrac{3}{2}h - h = \dfrac{h}{2}$

The percentage the diameter of the cylinder exceed its height 

$= \dfrac{{\dfrac{h}{2}}}{{h}} \times 100$

$= \dfrac{{100}}{2}$

$= 50\%$

8. $30$ circular plates, each of radius $14 cm$ and thickness $3cm$ are placed one above the another to form a cylindrical solid. Find : 

i) the total surface area 

Ans: Given, 

Radius of the base of the cylinder formed $\left( r \right)= 14{\text{cm}}$

Thickness $= 3{\text{cm}}$ 

Height of the cylinder formed $(h) = 30 \times 3 = 90{\text{cm}}$

Calculate the total surface area of the cylinder

Total surface area of the cylinder $= 2\pi r(r + h)$

$= 2 \times \dfrac{{22}}{7} \times 14(14 + 90)$

$= 2 \times \dfrac{{22}}{7} \times 14 \times 104$

$= 9152{\text{c}}{{\text{m}}^2}$

ii) volume of the cylinder so formed.

Ans: Calculate the volume of the cylinder

Volume of the cylinder formed $= \pi {r^2}h$

$V = \dfrac{{22}}{7} \times 14 \times 14 \times 90$

$V = 55440{\text{c}}{{\text{m}}^3}$

Introduction to Chapter 13

In Chapter 13 of Class 9 Maths- Surface Areas and Volumes, the definition of solids has been explained initially. Any object occupying a fixed space and volume is termed as a solid.  Examples would be cubes, cones, cuboids.  Then, the students learn about the different formulae for the different kinds of solids such as cube, cuboid, cylinders, cones, spheres, spherical shells, and hemispheres.

How Can I Prepare for the NCERT Class 9 Maths Test?

• Practice solving as many papers as possible for complete grasp over the concepts

• Refer to Vedantu.com and look for NCERT Exemplar for Class 9 Maths which have been solved by field experts

• Time yourself while solving each of these papers to master time management

• Try and understand the solutions in the book instead of mugging them up as they will ensure that the concepts have stuck.