NCERT Exemplar for Class 12 Physics Chapter 2 (Book Solutions)

MULTIPLE CHOICE QUESTIONS- I 

2.1 A capacitor of $4\mu F$ is connected as shown in the circuit (Fig. 2.1). The internal resistance of the battery is $0.5\Omega $. The amount of charge on the capacitor plates will be

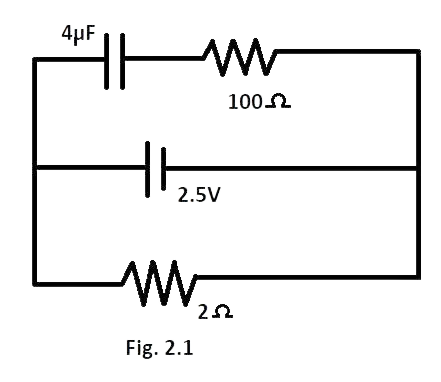
(a) $0$

(b)$4\mu C$

(c)$16\mu C$

(d)$8\mu C$

Ans: (d)$8\mu C$

As the Capacitor offers infinite resistance, the current from the cell will not flow across the capacitor branch. So current will flow across $2\Omega $ resistor branch.

$I = \dfrac{V}{{R + r}}$

$I = \dfrac{{2.5}}{{2 + 0.5}}$

$I = \dfrac{{2.5}}{{2.5}}$

$I = 1Amp$

So, the potential difference across $2\Omega $ resistance will be,

$V = IR$

$V = 2 \times 1$

$V = 2volt$

As the battery, capacitor and $2\Omega $branches are in parallel. So, the potential difference will remain the same across all the three branches. 

As the current does not flow through the capacitor branch, there will be no potential drop across the $10\Omega $ resistance.

So, the potential difference across $4\mu F$ capacitor is$2volt$.

$q = CV$

$q = 4\mu F \times 2$

$q = 8\mu C$

2.2 A positively charged particle is released from rest in a uniform electric field. The electric potential energy of the charge will

(a) Remains a constant because the electric field is uniform. 

(b) Increases because the charge moves along the electric field. 

(c) Decreases because the charge moves along the electric field. 

(d) Decreases because the charge moves opposite to the electric field. 

Ans: (c) Decreases because the charge moves along the electric field.

Equipotential surface is always perpendicular to the direction of the electric field. 

Positive charge experiences the force in the direction of the electric field. 

When a positive charge is released from rest in a uniform electric field, its velocity increases in the direction of the electric field. So, the kinetic energy increases, and the potential energy decreases due to conservation of energy. 

So the potential energy of a positively charged particle decreases because the charged particle moves in the direction of the field due to the force.

2.3 Figure 2.2 shows some equipotential lines distributed in space. A charged object is moved from point A to point B.

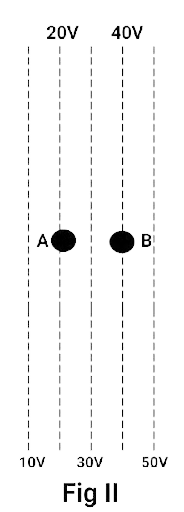
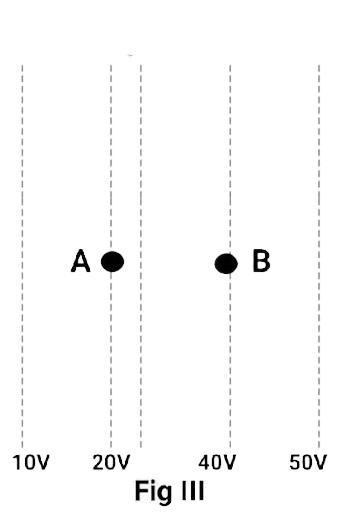
(a) The work done in Fig. (i) is the greatest. 

(b) The work done in Fig. (ii) is least. 

(c) The work done is the same in Fig. (i), Fig. (ii) and Fig. (iii). 

(d) The work done in Fig. (iii) is greater than Fig. (ii) but equal to that in Fig. (i)

Ans: (c) The work done is the same in Fig. (i), Fig. (ii) and Fig. (iii).

As the potential difference between A and B in all three figures is equal that is $20V$, so the work done $\Delta V \cdot q$by any charge moving from A to B surface will be equal.

2.4 The electrostatic potential on the surface of a charged conducting sphere is $100V$. Two statements are made in this regard: 

S1: At any point inside the sphere, electric intensity is zero. 

S2: At any point inside the sphere, the electrostatic potential is $100V$. 

Which of the following is a correct statement?

(a) S1 is true but S2 is false. 

(b) Both S1 & S2 are false. 

(c) S1 is true, S2 is also true and S1 is the cause of S2. 

(d) S1 is true, S2 is also true but the statements are independent. 

Ans: (c) S1 is true, S2 is also true and S1 is the cause of S2.

The relation between electric field intensity $E$ and potential $V$ is

$E =  - \dfrac{{dV}}{{dr}}$

Here, $E = 0$ inside the sphere then $ - \dfrac{{dV}}{{dr}} = 0$ i.e. $E = 0$. 

$E = 0$ inside the charged sphere, the potential is constant or $V = 100$ everywhere inside the sphere and it verifies the shielding effect also. 

Hence verifies the option (c). 

2.5 Equipotential at a great distance from a collection of charges whose total sum is not zero are approximately 

(a) Spheres. 

(b) Planes. 

(c) Paraboloids 

(d) Ellipsoids.

Ans: (a) Spheres

Here we have to find out the shape of the equipotential surface. These surfaces are perpendicular to the electric field lines. So there must be an electric field due to the collection of charge. 

The algebraic sum of all charges must not be zero. As it is given that the equipotential surface is at a great distance which means that space between the charges is negligible as compared to distance. 

So the collection of charges is considered as a point charge. 

The electric field lines from a point charge are radial. So the equipotential surface (perpendicular to the field lines) forms a sphere. 

It verifies that (a) is the correct Ans:

2.6 A parallel plate capacitor is made of two dielectric blocks in series. One of the blocks has thickness ${d_1}$ and dielectric constant ${k_1}$ and the other has thickness ${d_2}$ and dielectric constant ${k_2}$as shown in Fig. 2.3. This arrangement can be thought of as a dielectric slab of thickness $d = ({d_1} + {d_2})$and effective dielectric constant$k$. The $k$ is

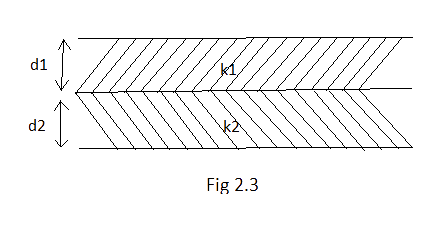
(a)$\dfrac{{{k_1}{d_1} + {k_2}{d_2}}}{{{d_1} + {d_2}}}$

(b) $\dfrac{{{k_1}{d_1} + {k_2}{d_2}}}{{{k_1} + {k_2}}}$

(c) $\dfrac{{{k_1}{k_2}({d_1} + {d_2})}}{{({k_1}{d_1} + {k_2}{d_2})}}$

(d) $\dfrac{{2{k_1}{k_2}}}{{{k_1} + {k_2}}}$

Ans: (c) $\dfrac{{{k_1}{k_2}({d_1} + {d_2})}}{{({k_1}{d_1} + {k_2}{d_2})}}$

Capacitance of a parallel plate capacitor filled with dielectric of constant ${k_1}$ and thickness ${d_1}$ is 

${C_1} = \dfrac{{{k_1}{\varepsilon _0}A}}{{{d_1}}}$

Similarly for other, 

${C_2} = \dfrac{{{k_2}{\varepsilon _0}A}}{{{d_2}}}$

As both the capacitors are in series, the equivalent capacitance $C$ is related as:

$\dfrac{1}{C} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}}$

$\dfrac{1}{C} = \dfrac{1}{{\dfrac{{{k_1}{\varepsilon _0}A}}{{{d_1}}}}} + \dfrac{1}{{\dfrac{{{k_2}{\varepsilon _0}A}}{{{d_2}}}}}$

$\dfrac{1}{C} = \dfrac{{{d_1}}}{{{k_1}{\varepsilon _0}A}} + \dfrac{{{d_2}}}{{{k_2}{\varepsilon _0}A}}$

\[\dfrac{1}{C} = \dfrac{1}{{{\varepsilon _0}A}}\left( {\dfrac{{{d_1}}}{{{k_1}}} + \dfrac{{{d_2}}}{{{k_2}}}} \right)\]

\[\dfrac{1}{C} = \dfrac{1}{{{\varepsilon _0}A}}\left( {\dfrac{{{k_2}{d_1} + {k_1}{d_2}}}{{{k_1}{k_2}}}} \right)\]

 So \[C = \dfrac{{{k_1}{k_2}{\varepsilon _0}A}}{{\left( {{k_2}{d_1} + {k_1}{d_2}} \right)}}\]  ……….. eq I

 $C' = \dfrac{{k{\varepsilon _0}A}}{d}$                  ……….. eq II 

Here $d = ({d_1} + {d_2})$ 

So, multiply the numerator and denominator of eq I with$({d_1} + {d_2})$,

\[C = \dfrac{{{k_1}{k_2}{\varepsilon _0}A}}{{\left( {{k_2}{d_1} + {k_1}{d_2}} \right)}} \cdot \dfrac{{({d_1} + {d_2})}}{{({d_1} + {d_2})}}\]

\[C = \dfrac{{{k_1}{k_2}({d_1} + {d_2})}}{{\left( {{k_2}{d_1} + {k_1}{d_2}} \right)}} \cdot \dfrac{{{\varepsilon _0}A}}{{({d_1} + {d_2})}}\]  ………. eq III 

On comparing eq II and eq III, the dielectric constant of new capacitor is: 

$\dfrac{{{k_1}{k_2}({d_1} + {d_2})}}{{({k_1}{d_1} + {k_2}{d_2})}}$

It verifies that the correct Ans is (c). 

MULTIPLE CHOICE QUESTION-II MORE THAN ONE OPTION 

2.7 Consider a uniform electric field in the \[\widehat z\] direction. The potential is a constant 

(a) in all space. 

(b) for any $x$ for a given$z$. 

(c) for any $y$ for a given$z$. 

(d) on the $x - y$plane for a given $z$.

Ans: (b) for any $x$ for a given$z$, (c) for any $y$ for a given$z$ and (d) on the $x - y$plane for a given$z$.

As we know that equipotential surfaces are perpendicular to the direction of electric field lines. 

Here the electric field is in \[ + \widehat z\] direction.

So, equipotential surfaces will be in the plane perpendicular to the$z - axis$ i.e. along the $x - y$plane which includes any $x$ or $y$ axes. 

So the Anss (b), (c) and (d) are verified respectively.

2.8 Equipotential surfaces

(a) are closer in the regions of large electric fields as compared to the regions of lower electric fields.

(b) will be more crowded near sharp edges of a conductor.

(c) will be more crowded near regions of large charge densities.

(d) will always be equally spaced.

Ans: (a) are closer in the regions of large electric fields as compared to the regions of lower electric fields, (b) will be more crowded near sharp edges of a conductor and (c) will be more crowded near regions of large charge densities. 

We know that on any two points of equipotential surface, potential difference is zero or of equal i.e.

$E =  - \dfrac{{dV}}{{dr}}$

The electric field intensity is inversely proportional to the separation between equipotential surfaces. So the equipotential surfaces are closer in the regions of large electric fields. 

Thus, it verifies Ans (a).

The electric field is larger near the sharp edge, due to larger charge density as A is very small i.e.

$\sigma  = \dfrac{q}{A}$

So the equipotential surfaces are closer or crowded.

Thus, it verifies Ans (b).

As the electric field $E = \dfrac{{kq}}{{{r^2}}}$ and potential or field decreases as size of body increases or vice- versa (case of earth), the equipotential surfaces will be more crowded if the charge density $\sigma  = \dfrac{q}{A}$ increases. 

Thus, it verifies the Ans (c).

As the equipotential surface depends on distance $r$by$E =  - \dfrac{{dV}}{r}$ and $V = \dfrac{{kq}}{r}$ .

Equipotential surface depends on charge density at that place which is different at different places, so equipotential surfaces are not equally spaced all over.

2.9 The work done to move a charge along an equipotential from A to B

(a) cannot be defined as $ - \int\limits_A^B {E.dl} $

(b) must be defined as $ - \int\limits_A^B {E.dl} $

(c) is zero.

(d) can have a non-zero value.

Ans: (c) is zero.

As the potential on equipotential surface does not change

So ${V_2} - {V_1} = 0$

And $w = ({V_2} - {V_1})q$

So, work done on moving a charge is zero, verifies Ans (c).

We know the work done by a charge $q$ moving in electric field is

\[dW = F.dl\]

\[\smallint  = \int {qE.dl} \]

\[W = q\int {E.dl} \]

So, \[W \ne \int {E.dl} \] or Ans (b) is wrong.

Ans (a) and (b) can be true only when $q =  + 1C$which is not given in question.

2.10 In a region of constant potential

(a) the electric field is uniform

(b) the electric field is zero

(c) there can be no charge inside the region.

(d) the electric field shall necessarily change if a charge is placed outside the region.

Ans: (b) the electric field is zero and (c) there can be no charge inside the region.

Constant potential $ \Rightarrow dV = 0$ so by relation$E =  - \dfrac{{dV}}{{dr}}$ , $E = 0$ i.e. the electric field is not uniform which discards the Ans (a) and agree with the Ans (b).

As the potential may also be present outside the charge, there can be no charge inside the region of constant potential. 

Thus, this verifies Ans (c).

If a charge is placed outside the region, the potential difference or electric field in the region will change. 

Thus, this makes Ans (d) incorrect.

2.11 In the circuit shown in Fig. 2.4 initially key ${K_1}$ is closed and key ${K_2}$ is open. Then ${K_1}$is opened and ${K_2}$ is closed (order is important). [ Take  ${Q_1}'$ and ${Q_2}'$ as charges on

${C_1}$ and ${C_2}$ and ${V_1}$ and ${V_2}$ as voltage respectively].

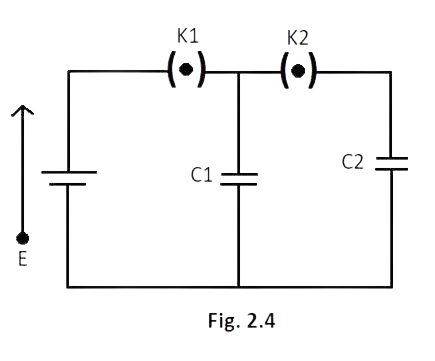
Then

(a) charge on ${C_1}$ gets redistributed such that ${V_1} = {V_2}$

(b) charge on ${C_1}$gets redistributed such that ${Q_1}' = {Q_2}'$ 

(c) charge on ${C_1}$ gets redistributed such that ${C_1}{V_1} + {C_2}{V_2} = {C_1}E$

(d) charge on ${C_1}$ gets redistributed such that ${Q_1}' + {Q_2}' = Q$

Ans: (a) charge on ${C_1}$ gets redistributed such that ${V_1} = {V_2}$ and (d) charge on ${C_1}$ gets redistributed such that ${Q_1}' + {Q_2}' = Q$

When ${K_1}$is closed keeping ${K_1}$open, the capacitor ${C_1}$ gets charged by battery of emf$E$. Now, when ${K_1}$ opens ${C_1}$ remains charged. When ${K_2}$ closes keeping ${K_1}$ open, ${C_2}$ gets charged by redistribution of charges of ${C_1}$between ${C_1}$ and ${C_2}$. 

Let the charge on${C_1}$ which is charged by battery be $Q$, then after redistribution of charge  $Q = {Q_1}' + {Q_2}'$  by law of conservation of charge. 

So the Ans (d) is verified. 

As ${C_1}$ and ${C_2}$ both are in parallel combination, so their potential will be equal i.e. ${V_1} = {V_2}$ . 

Thus, it verifies the Ans (a).

2.12 If a conductor has a potential $V \ne 0$ and there are no charges anywhere else outside, then 

(a) there must be charges on the surface or inside itself. 

(b) there cannot be any charge in the body of the conductor. 

(c) there must be charges only on the surface. 

(d) there must be charges inside the surface. 

Ans: (a) there must be charges on the surface or inside itself.  (b) there cannot be any charge in the body of the conductor.

As the excess charge can reside only on the surface of a conductor and inside net positive and negative charge is zero. 

Any charge can reside inside the hollow shell or body. So this verifies Ans (a) and discards Ans (c).

Inside the solid material of conducting body there is no charge, it comes to outer surface. So this verifies Ans (b) and discards Ans (d).

2.13 A parallel plate capacitor is connected to a battery as shown in Fig. 2.5. Consider two situations: 

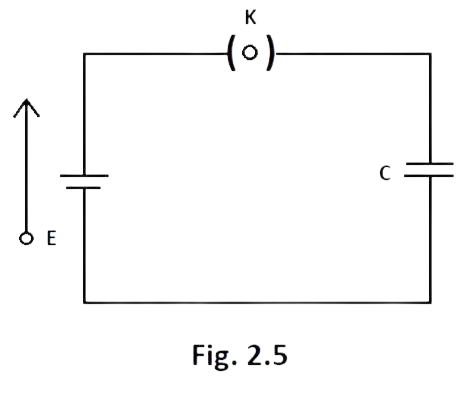
A: Key $K$ is kept closed and plates of capacitors are moved apart using insulating handle. 

B: Key $K$ is opened and plates of capacitors are moved apart using insulating handle.

Choose the correct option(s). 

(a) In A: $Q$ remains same but $C$ changes. 

(b) In B: $V$ remains same but $C$ changes. 

(c) In A: $V$ remains same and hence $Q$ changes. 

(d) In B: $Q$remains same and hence $V$ changes. 

Ans: (c) In A: $V$ remains same and hence $Q$ changes and (d) In B: $Q$remains same and hence $V$ changes.

(A) In situation A:  When the space between the plates of capacitor increases, the capacitance decreases by relation$C = \dfrac{{K{\varepsilon _0}A}}{d}$ , but battery remains same i.e. potential difference across plate remains ‘$V$’ same. So by $Q = CV$ relation, $Q$ also decreases which verify the Ans (c) and discards the Ans (a). 

(B) Now for situation B: $K$ is open and capacitance decreases by moving apart the plates of capacitor, so by relation $Q = CV$, here $K$ is open so charge $Q$ remains same in turn $V$ will increase on decreasing $C$ hence Ans (d) is verified.

VERY SHORT ANSWER TYPE QUESTIONS 

2.14 Consider two conducting spheres of radii ${R_1}$ and ${R_2}$ with${R_1} > {R_2}$ . If the two are at the same potential, the larger sphere has more charge than the smaller sphere. State whether the charge density of the smaller sphere is more or less than that of the larger one.

Ans: Let ${Q_1}$ and ${Q_2}$ be the charges on radii ${R_1}$ and ${R_2}$ we know that

$V = \dfrac{1}{{4\pi \varepsilon }}\dfrac{{{Q_1}}}{{{R_1}}}$ and $V = \dfrac{1}{{4\pi \varepsilon }}\dfrac{{{Q_2}}}{{{R_2}}}$

As${V_1} = {V_2}$, so

$ \Rightarrow \dfrac{1}{{4\pi \varepsilon }}\dfrac{{{Q_1}}}{{{R_1}}} = \dfrac{1}{{4\pi \varepsilon }}\dfrac{{{Q_2}}}{{{R_2}}}$

$ \Rightarrow \dfrac{{{Q_1}}}{{{R_1}}} = \dfrac{{{Q_2}}}{{{R_2}}}$

$ \Rightarrow \dfrac{{{Q_1}}}{{{Q_2}}} = \dfrac{{{R_1}}}{{{R_2}}}$

$ \Rightarrow \dfrac{{{\sigma _1} \times 4\pi {{({R_1})}^2}}}{{{\sigma _2} \times 4\pi {{({R_2})}^2}}} = \dfrac{{{R_1}}}{{{R_2}}}$

$ \Rightarrow \dfrac{{{\sigma _1}}}{{{\sigma _2}}} = \dfrac{{{R_2}}}{{{R_1}}}$

Since ${R_1} > {R_2}$it follows that

${\sigma _1} < {\sigma _2}$

i.e. the charge density of smaller sphere is less than that of larger sphere.

2.15 Do free electrons travel to region of higher potential or lower potential?

Ans: As free electrons have negative charge so the direction of their flow will be opposite to positive charge i.e. free electrons will move from lower potential to higher potential.

2.16 Can there be a potential difference between two adjacent conductors carrying the same charge?

Ans: If the current flowing through the two conductors is same then they both may be considered in series. 

So according to Ohm’s law becomes 

$V\alpha R$ 

i.e. if the resistances (which depends on $\rho $, $I$ and $A$) are different then the potential difference will also be different.

So there can be a potential difference between two adjacent conductors carrying the same charge or current if either their length or area of cross-section ($A$) and resistivity are different.

2.17 Can the potential function have a maximum or minimum in free space?

Ans: In the absence of free space or atmosphere, the phenomenon of electric field or potential leakage is cannot be prevented. Hence, the potential function do not have maximum or minimum in free space.

2.18 A test charge $q$ is made to move in the electric field of a point charge $Q$ along two different closed paths (Fig. 2.6). First path has sections along and perpendicular to lines of electric field. Second path is a rectangular loop of the same area as the first loop. How the work done does is compare in the two cases?

Ans: We know that electrostatic work done is conservative. So work done in closed loop is always zero, it does not depend on the nature of closed path.

SHORT ANSWER TYPE QUESTIONS

2.19 Prove that a closed equipotential surface with no charge within itself must enclose an equipotential volume.

Ans: Let us consider that inside the enclosed equipotential surface, potential is not same. Let the potential inside the equipotential surface is different to that on the equipotential surface, causing in a potential gradient$\dfrac{{dV}}{{dr}} = E$. So the electric field which exists inside surface is equal to$E = \dfrac{{dV}}{{dr}}$ .

The electric field lines pointing inward or outward from the surface are perpendicular to the equipotential surfaces or the field lines cannot be on the equipotential surface.

The field lines can be on the equipotential surface if field lines can originate from the charge inside, which contradicts the original assumption. Hence, the entire volume inside equipotential surface has no charge.

2.20 A capacitor has some dielectric between its plates, and the capacitor is connected to a DC source. The battery is now disconnected and then the dielectric is removed. State whether the capacitance, the energy stored in it, electric field, charge stored and the voltage will increase, decrease, or remain constant.

Ans: $C = \dfrac{{K{\varepsilon _0}A}}{d}$

As $k$ is positive and more than one, so by removing dielectric slab, and keeping $A$ and $d$constant, capacitance of capacitor will decrease. When the battery and dielectric slab from capacitor is removed, the charge remains same as it was when battery connected earlier.

As the energy stored in capacitor is$\dfrac{{{q^2}}}{{2C}}$ . When capacitance $C$ is decreased by removing dielectric slab but $q$ remains same, so the energy stored in capacitor will increase.

We know that$V = \dfrac{q}{C}$ , where $q$is same and $C$ is decreased so potential will increase.

As$E = \dfrac{V}{d}$ , distance between plates of capacitor is same and potential is increased as discussed above, so electric field between the plates of capacitor will increase.

2.21 Prove that, if an insulated, uncharged conductor is placed near a charged conductor and no other conductors are present, the uncharged body must be intermediate in potential between that of the charged body and that of infinity.

Ans: Consider a charged body (A) (say with positive charge) and an insulated uncharged conductor (B) is placed near the charged conductor (A) as shown in the figure:

As $V = \dfrac{{kq}}{r}$ where $k$ and $q$ are constants, so

$V\alpha \dfrac{1}{r}$ or infinity, $V \to 0$

Uncharged conductor is between charged conductor and infinity, so potential decreases from body A to infinity.

So the potential of uncharged body varies between potential of A and infinity.

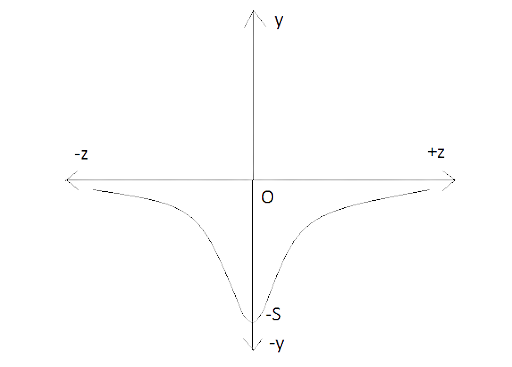
2.22 Calculate potential energy of a point charge $ - q$ placed along the axis due to a charge $ + Q$ uniformly distributed along a ring of radius$R$. Sketch potential energy as a function of axial distance $z$ from the center of the ring. Looking at graph, can you see what would happen if $ - q$ is displaced slightly from the center of the ring (along the axis)?

Ans: Let us consider a ring of radius $R$ having charge $ + Q$ distributed uniformly over the ring. Also there is a point $P$ at distance a $z$ on the axis passing through center $O$ and perpendicular to plane of the ring.

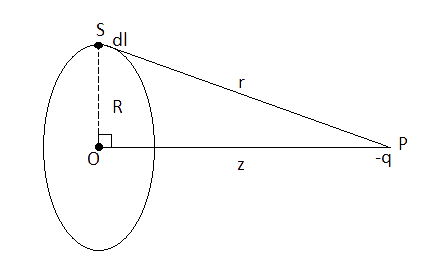
Again consider an element of ring at $S$of length $dl$ having charge $dq$ and $SP$ is equal to $r$.Then the potential energy due to the element $dl$ at $P$ if $dq$ is the charge on element $dl$ of ring is $dV = \dfrac{{ - kdq}}{r}$ where $k = \dfrac{1}{{4\pi {e_0}}}$ and as $Q$ is positive charge, so potential due to the charge $dq$ will be negative.

Charge on$2\pi R$ length of the ring $ = Q$

Charge on $dl$ length of the ring is $dq = \dfrac{Q}{{2\pi R}}dl$

So potential due to element $dl$ at $P$

$dV = \dfrac{{ - kQdl}}{{2\pi Rr}}$

Since $dW = dV \cdot q$ and $r = \sqrt {{R^2} + {z^2}} $

So, $dW = \dfrac{{ - kQqdl}}{{2\pi R\sqrt {{R^2} + {z^2}} }}$

Integrating both sides, over a ring, we have

$\int\limits_0^\pi  {dW}  =  - \int\limits_0^{2\pi R} {\dfrac{{kqQdl}}{{2\pi R\sqrt {{R^2} + {z^2}} }}} $

$W =  - \dfrac{{kqQ2\pi R}}{{2\pi RR\sqrt {1 + \dfrac{{{z^2}}}{{{R^2}}}} }}$

This work done gets converted into P.E. at P, so P.E. is

$V = \dfrac{{ - Qq}}{{4\pi {\varepsilon _0}R\sqrt {1 + \dfrac{{{z^2}}}{{{R^2}}}} }}$

Let $\dfrac{{Qq}}{{4\pi {\varepsilon _0}R}} = S$(a new constant)

$V = \dfrac{{ - S}}{{{{\left[ {1 + \dfrac{{{z^2}}}{{{R^2}}}} \right]}^{^{\dfrac{1}{2}}}}}}$

At $z =  - \infty $

${V_2} = \dfrac{{ - S}}{{{{\left[ {1 + \dfrac{{{z^2}}}{{{R^2}}}} \right]}^{^{\dfrac{1}{2}}}}}}$

Hence, $z >  >  > R$

Also, ${z^2} >  >  > {R^2}$

${\left( {1 + \dfrac{{{z^2}}}{{{R^2}}}} \right)^{\dfrac{1}{2}}} = \infty $

So, ${V_{ - z}} = \dfrac{{ - S}}{\infty } \to 0$

${V_{ - z}} \to {0^\infty }$

${V_{ + z}} \to 0$

At $z = 0$

$V =  - S$

2.23 Calculate potential on the axis of a ring due to charge Q uniformly distributed along the ring of radius R.

Ans: Let us consider a ring of radius $R$ having charge $ + Q$ distributed uniformly. Also there is a point $P$ at distance $z$ on its axis passing through center $O$ and perpendicular to plane of ring. 

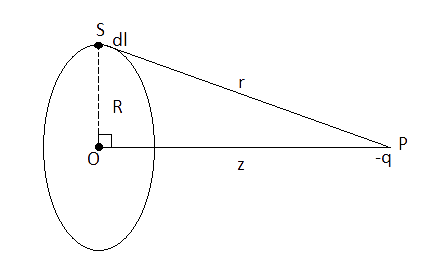
Again consider an element on ring at $S$of length $dl$ having a charge $dq$ and $SP$ is equal to$r$. Then potential energy due to element $dl$ at$P$ is,

$dV = \dfrac{{ - kdq}}{r}$ where  $k = \dfrac{1}{{4\pi {\varepsilon _0}}}$

Charge on $2\pi R$ length of ring $ = Q$

Charge on $dl$ length of ring $ = \dfrac{Q}{{2\pi R}}dl$

So potential due to element $dl$ at$P$,

$dV = \dfrac{{ - k \cdot Q \cdot dl}}{{2\pi R}}$

Integrating over a ring the potential at$P$, ${V_P}$

\[\int\limits_0^V {d{V_P} = \int\limits_0^{2\pi R} {\dfrac{{kQdl}}{{2\pi Rr}}} } \] where $r = \sqrt {{R^2} + {z^2}} $

${V_P} = \dfrac{{kQ2\pi R}}{{2\pi R\sqrt {{R^2} + {z^2}} }}$

${V_P} = \dfrac{Q}{{4\pi {\varepsilon _0}\sqrt {{R^2} + {z^2}} }}$

LONG ANSWER TYPE QUESTIONS

2.24 Find the equations of the equipotential surfaces for an infinite cylinder of radius ${r_0}$ and carrying a charge of linear density$\lambda $.

Ans: Consider a Gaussian cylindrical dotted surface $S$at a distance $r$ from the center of the cylinder of radius ${r_0}$ of the infinite length.

The electric field lines are radial and perpendicular to the surface.

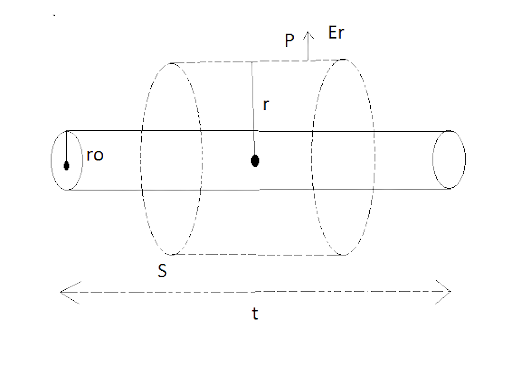
Let electric field intensity on Gaussian surface at $P$ is$E$, and total charge $q$ on cylinder will be$q = \lambda l$.

So, by Gauss’s law,

$\oint\limits_S {{E_r}ds = \dfrac{{\lambda l}}{\varepsilon } \Rightarrow \left[ {{E_r}\cos \theta } \right]_0^{2\pi l} = \dfrac{{\lambda l}}{{{\varepsilon _ \cap }}}} $

$E$, $2\pi rl\cos {90^ \circ } = \dfrac{{\lambda l}}{{{\varepsilon _{}}}}$ [$\angle \theta $ is between ${E_r}$ and curved surface of dotted cylinder is${90^ \circ }$]

${E_r} = \dfrac{\lambda }{{2\pi r{\varepsilon _0}}}$

We know that electric field ${E_r}$at distance r from center of cylinder${E_r} = \dfrac{{ - dV}}{{dr}}$.

So the potential difference $dV$ at distance ${r_0}$and $r$ from the center of cylinder is,

$dV = {E_r} \cdot dr\left[ {\because E = \dfrac{{ - dV}}{{dr}}} \right]$

$V\left( r \right) - V\left( {{r_0}} \right) =  - \int {{E_r} \cdot dr} $

\[V\left( r \right) - V\left( {{r_0}} \right) =  - \int\limits_{{r_0}}^r {\dfrac{\lambda }{{2\pi {\varepsilon _0}r}} \cdot dr = } \dfrac{{ - \lambda }}{{2\pi {\varepsilon _0}}}\int\limits_{{r_0}}^r {\dfrac{{dr}}{r} = \dfrac{{ - \lambda }}{{2\pi {\varepsilon _0}}}\left[ {{{\log }_e}r} \right]_0^r} \]

\[V\left( r \right) - V\left( {{r_0}} \right) = \dfrac{{ - \lambda }}{{2\pi {\varepsilon _0}}}\left[ {{{\log }_e}r - {{\log }_e}{r_0}} \right] = \dfrac{{ - \lambda }}{{2\pi {\varepsilon _0}}}\left[ {{{\log }_e}r} \right]_{{r_0}}^r\]

\[{\log _e}\dfrac{r}{{{r_0}}} = \dfrac{{ - 2\pi {\varepsilon _0}}}{\lambda }\left[ {V\left( r \right) - V\left( {{r_0}} \right)} \right]\]

\[\dfrac{r}{{{r_0}}} = {e^{\dfrac{{ - 2\pi {\varepsilon _0}}}{\lambda }\left[ {V\left( r \right) - V\left( {{r_0}} \right)} \right]}}\]

\[r = {r_0}{e^{\dfrac{{ - 2\pi {\varepsilon _0}}}{\lambda }\left[ {V\left( r \right) - V\left( {{r_0}} \right)} \right]}}\]

So the equipotential surfaces are the coaxial curved surfaces of cylinders with given cylinder of radius $r$ related as above.

2.25 Two point charges of magnitude $ + q$ and $ - q$are placed at $\left( { - \dfrac{d}{2},0,0} \right)$ and $\left( {\dfrac{d}{2},0,0} \right)$ respectively. Find the equation of the equipotential surface where the potential is zero.

Ans: The potential due to charge $ + q$ and $ - q$ will be zero in between the line joining the two charges. Let zero potential is at$S$.

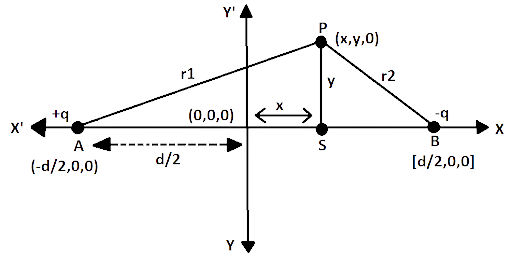
Then the equipotential surface will pass through $S$ and perpendicular to line joining the two chargers or$AB$.

So, $r_1^2 = A{S^2} + S{P^2}$

     $r_1^2 = {\left( {x + \dfrac{d}{2}} \right)^2} + {y^2}$

     ${r_1} = \sqrt {{{\left( {x + \dfrac{d}{2}} \right)}^2} + {y^2}} $

Similarly, ${r_2} = \sqrt {{{\left( {x - \dfrac{d}{2}} \right)}^2} + {y^2}} $

So net potential at $P = 0$

$\dfrac{{kq}}{{{r_1}}} + \dfrac{{k( - q)}}{{{r_2}}} = 0$ where $k = \dfrac{1}{{4\pi {\varepsilon _0}}}$

\[ \Rightarrow kq\left[ {\dfrac{1}{{{r_1}}} - \dfrac{1}{{{r_2}}}} \right] = 0{\text{ }}\left[ {\because kq \ne 0} \right]\]

\[ \Rightarrow \dfrac{1}{{{r_1}}} - \dfrac{1}{{{r_2}}} = 0{\text{ }}\]

\[ \Rightarrow \dfrac{1}{{{r_1}}} = \dfrac{1}{{{r_2}}}{\text{  }} \Rightarrow {r_1} = {r_2}\]

\[ \Rightarrow {\left( {x + \dfrac{d}{2}} \right)^2} + {y^2} = {\left( {x - \dfrac{d}{2}} \right)^2} + {y^2}\]

\[ \Rightarrow {\left( {x + \dfrac{d}{2}} \right)^2} = {\left( {x - \dfrac{d}{2}} \right)^2}\]

\[ \Rightarrow {x^2} + \dfrac{{{d^2}}}{4} + dx = {x^2} + \dfrac{{{d^2}}}{4} - dx\]
$2d \ne 0$$2dx = 0$

$\therefore x = 0$

So the equipotential surface will be perpendicular to $x - axis$ and passing through $x = 0$i.e., origin in $Y - Z$plane.

2.26 A parallel plate capacitor is filled by a dielectric whose relative permittivity varies with the applied voltage ($U$) as $\varepsilon  = \alpha U$ where$\alpha  = 2{V^{ - 1}}$. A similar capacitor with no dielectric is charged to${U_0} = 78V$. It is then connected to the uncharged capacitor with the dielectric. Find the final voltage on the capacitors.

Ans: Let $C$ be the capacitance of capacitor ${C_1}$ without dielectric then charge ${q_1} = CU$ where $U$is the final potential of the ${C_1}$when connected to ${C_2}$ the capacitor filled with dielectric ${\varepsilon _0}$

${C_2} = \varepsilon C$

${q_2} = \varepsilon CU$

$ = \alpha UCU$

Initial charge \[{q_0}\]of ${C_1}$ when charged at potential of ${U_0} = 78V$is,

${q_0} = C{U_0} = 78C$

By the law of conservation of charge

\[{q_0} = {q_1} + {q_2}\]

\[78C = CU + \alpha  \cdot C{U^2}\]

\[78 = U + \alpha {U^2}{\text{  }}\left[ {\alpha  = 2{\text{ }}per{\text{ }}volt} \right]\]

\[\therefore  = U + 2{U^2}\]

Or \[2{U^2} + U - 78 = 0\]

$U = \dfrac{{ - 1 \pm \sqrt {1 - 4.2( - 78)} }}{{2.2}} = \dfrac{{ - 1 \pm \sqrt {1 - 624} }}{4}$

$U = \dfrac{{ - 1 \pm \sqrt {625} }}{4} = \dfrac{{ - 1 \pm 25}}{4}$

$U = \dfrac{{ - 1 \pm 25}}{4}$  as $U$is positive

$U = \dfrac{{24}}{4} = 6volts$

The final potential on both the capacitors will be$6volts$.

2.27 A capacitor is made of two circular plates of radius $R$ each, separated by a distance$d <  < R$. The capacitor is connected to a constant voltage. A thin conducting disc of radius $r <  < R$ and thickness $'t' <  < r$ is placed at a center of the bottom plate. Find the minimum voltage required to lift the disc if the mass of the disc is$m$.

Ans: Let $A$ and $B$ are circular plates of radius $R$ separated by distance $d <  < R$kept horizontally.

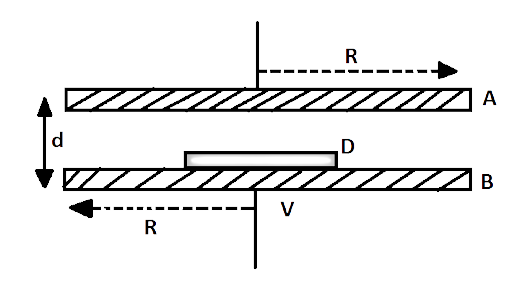
A thin conducting disc $D$ of radius $r <  < R$of thickness $'t'$ is placed concentrically on lower plate $B$ as shown in figure.

Let plate $A$ and $B$ charged with potential$V$.

The magnitude of electric field $E$ between plates of capacitor is

$E = \dfrac{V}{d}{\text{  }}\left[ {\because E = \dfrac{{ - dV}}{{dr}}} \right]$

Consider a Gaussian surface along circular disc$D$.

By Gauss’s law, $\oint {E \cdot ds = } \dfrac{{q'}}{{{\varepsilon _0}}}$

$\dfrac{V}{d}\pi {r^2} = \dfrac{{q'}}{{{\varepsilon _0}}}$

$q'$is the charge conducted by plate $B$ to disc $D$ during charging. Nature of charge on plate $B$ and disc will be same so repulsive force acts between $B$ and$D$.

So, the charge on disc $D = q' = \dfrac{V}{d}\pi {r^2}{\varepsilon _0}$

Electrostatic repulsive force acting on disc in upward direction

$F = q'E = \dfrac{V}{d}\pi {r^2}{\varepsilon _0} \cdot \dfrac{V}{d} = \dfrac{{{V^2}}}{{{d^2}}}\pi {r^2}{\varepsilon _0}$

This repulsive force will be balanced by weight mg of disc$D$.

$mg = \dfrac{{{V^2}}}{{{d^2}}}\pi {r^2}{\varepsilon _0}$

${V^2} = \dfrac{{mg{d^2}}}{{\pi {r^2}{\varepsilon _0}}}$

2.28 (a) In a quark model of elementary particles, a neutron is made of one up quarks $\left[ {{\text{charge }}\left( {\dfrac{2}{3}} \right)e} \right]$ and two down quarks $\left[ {{\text{charge }}\left( { - \dfrac{1}{3}} \right)e} \right]$ . Assume that they have a triangle configuration with side length of the order of ${10^{ - 15}}m$. Calculate electrostatic potential energy of neutron and compare it with its mass $939MeV$.

Ans:  ${q_d} =  - \dfrac{1}{3}e$ (Charge on down quark)

${q_u} =  + \dfrac{2}{3}e$ (Charge on up quark)

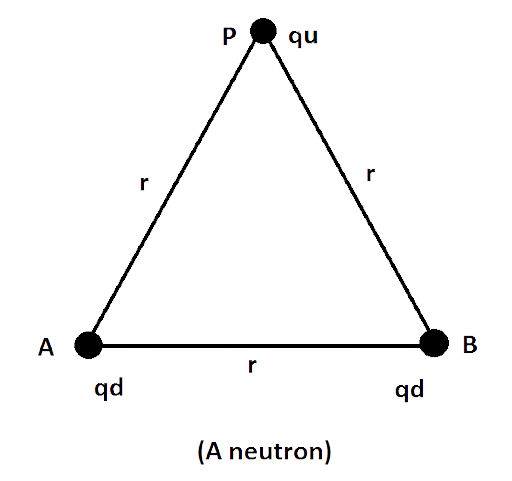
Potential energy $U = \dfrac{{k{q_1}{q_2}}}{r}$

Where, $k = \dfrac{1}{{4\pi {\varepsilon _0}}}$

$U = \dfrac{{k{q_1}{q_2}}}{r} + \dfrac{{k{q_1}{q_3}}}{r} + \dfrac{{k{q_2}{q_3}}}{r}$

\[\therefore {U_n} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{\left( { - {q_d}} \right)\left( { - {q_d}} \right)}}{r} + \dfrac{{\left( { - {q_d}} \right){q_u}}}{{4\pi {\varepsilon _0}}} + \dfrac{{{q_u}\left( { - {q_d}} \right)}}{{4\pi {\varepsilon _0}r}}\]

${U_n} = \dfrac{{{q_d}}}{{4\pi {\varepsilon _0}r}}\left[ { + {q_d} - {q_u} - {q_u}} \right]$ [Talking sign of charge]

${U_n} = \dfrac{{{q_d}}}{{4\pi {\varepsilon _0}r}}\left[ { + {q_d} - 2{q_u}} \right] = \dfrac{{9 \times {{10}^9} \times \dfrac{1}{3}e}}{{{{10}^{ - 15}}}}\left[ {\dfrac{1}{3}e - 2 \times \dfrac{2}{3}e} \right]$

[Natural sign of charges is already taken]

$\dfrac{{9 \times {{10}^9} \times e}}{{3 \times {{10}^{ - 15}}}} \times \dfrac{e}{3}\left[ {1 - 4} \right]{\text{ joule}}$

$\dfrac{{ - 3 \times 9 \times {{10}^9} \times 1.6 \times {{10}^{ - 19}}}}{{9 \times {{10}^{ - 15}}}}e{\text{ joule}}$

\[U =  - 0.48{\text{ }}MeV\]

So, charges inside neutron \[\left[ {1{q_u}{\text{ }}and{\text{ }}2{q_d}} \right]\] are attracted by energy of\[0.48{\text{ }}MeV\].

Energy released by a neutron when converted into energy is\[939{\text{ }}MeV\].

∴ required ratio \[ = \dfrac{{1 - 0.481MeV}}{{939MeV}} = 0.0005111{\text{ }} = 5.11 \times {10^{ - 4}}\]

(b) Repeat the above exercise for a proton which is made of two up and one down quark.

Ans: P.E. Of proton consists of 2 up and 1 down quark

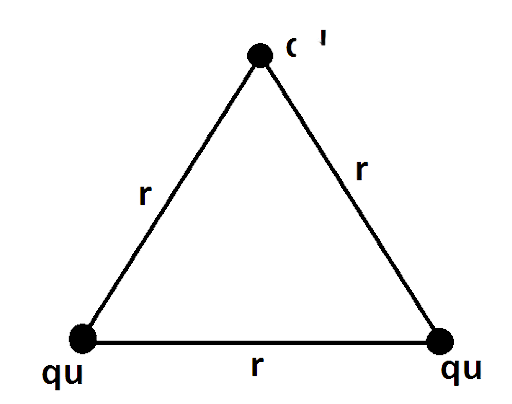
\[r = {\text{ }}{10^{ - 15}}m\]

${q_d} =  - \dfrac{1}{3}e{\text{ , }}{{\text{q}}_{\text{u}}}{\text{ = }}\dfrac{2}{3}e$

\[{U_p} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{q_u} \times {q_u}}}{r} + \dfrac{{{q_u}( - {q_d})}}{{4\pi {\varepsilon _0}r}} + \dfrac{{{q_u}( - {q_d})}}{{4\pi {\varepsilon _0}r}}\]

\[{U_p} = \dfrac{{{q_u}}}{{4\pi {\varepsilon _0}r}}\left[ {{q_u} - {q_d} - {q_d}} \right]\]

\[{q_2} = \sigma  \cdot {A_2} = \sigma  \cdot 4\pi {\left( {2R} \right)^2} = \sigma  \cdot 4\pi {R^2} \cdot 4 = 4{q_1}\]\[{U_p} = \dfrac{{{q_u}}}{{4\pi {\varepsilon _0}r}}\left[ {{q_u} - 2{q_d}} \right] = \dfrac{{9 \times {{10}^9}}}{{{{10}^{ - 15}}}}\dfrac{2}{3}e\left[ {\dfrac{2}{3}e - 2 \cdot \dfrac{1}{3}e} \right] = 0\]

${q_1}'$

$\therefore {q_1} = \sigma  \cdot {A_1} = \sigma  \cdot 4\pi {R^2}$

2.29 Two metal spheres, one of radius $R$ and the other of radius$2R$, both have same surface charge density$\sigma $. They are brought in contact and the${q_2}'$n separated. What will be new surface charge densities on them?

Ans: Let the su${q_2}$rface charge density of both the spheres be $\sigma $ and their charges are ${q_1}$and 

Bot${V_1} = {V_2}\left( {\because V = \dfrac{{kq}}{r}} \right)$h charged spheres are kept in co$\dfrac{{k{q_1}}}{R} = \dfrac{{k{q_2}}}{{2R}}\left[ {\because k = \dfrac{1}{{4\pi {\varepsilon _0}}}} \right]$n${q_1}'$tact, so charge flows between them and their potential will become equal.

Let the charges on them now be and.

So, 

So ${q_2}'$

Where  and  are the charges on spheres after redistribution of charges

$\dfrac{{{q_1}}}{R} = \dfrac{{{q_2}}}{{2R}}$

$\therefore {q_2}' = 2{q_1}'$ ………………….. I

By the law of conservation of charges

${q_1} + {q_2} = {q_1}' + {q_2}'$

${q_1} + 4{q_1} = {q_1}' + 2{q_1}'$ (From equation I)

$5{q_1} = 3{q_1}'$

${q_1} = \dfrac{{20}}{3}\pi {R^2}\sigma $

${\sigma _1} = \dfrac{{{q_1}}}{{{A_1}}} = \dfrac{{\dfrac{{20}}{3}\pi {R^2}\sigma }}{{4\pi {R^2}}} = \dfrac{5}{3}\sigma $

${\sigma _1} = \dfrac{{{q_2}}}{{{A_2}}} = \dfrac{{2 \cdot {q_1}}}{{4\pi {{(2R)}^2}}} = \dfrac{{2 \cdot \dfrac{{20}}{3}\pi {R^2}\sigma }}{{4\pi  \cdot 4{R^2}}} = \dfrac{5}{6}\sigma $

Hence, ${\sigma _1} = \dfrac{5}{3}\sigma $ and ${\sigma _2} = \dfrac{5}{6}\sigma $

2.30 In the circuit shown in Fig. 2.7, initially ${K_1}$is closed and ${K_2}$ is open. What are the charges on each capacitor? 

Then ${K_1}$was opened and ${K_2}$was closed (order is important), What will be the charge on each capacitor now? $\left[ {C = 1\mu F} \right]$

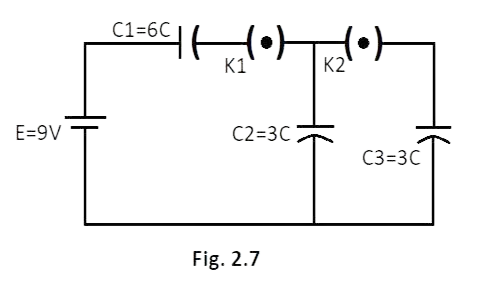
Ans: When ${K_2}$is open and ${K_1}$is closed the capacitors ${C_1}$and ${C_2}$ will charge and potential will develops across them i.e. ${V_1}$ and ${V_2}$ respectively which will be equal to the potential of battery.

$\therefore {V_1} + {V_2} = 9$ ............................... I

$\because V = \dfrac{q}{C}$

So, $V\alpha \dfrac{1}{C}$ and

$\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{{C_2}}}{{{C_1}}}$

$\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{3C}}{{6C}}$

$3{V_2} = 6{V_1}$

${V_2} = 2{V_1}$ ……………………II 

From Equations I and I

${V_1} + 2{V_1} = 9$

$3{V_1} = 9$

${V_1} = 3volts$

${V_2} = 2 \times 3volt$

     $ = 6volt$

$\therefore {q_1} = {C_1}{V_1}$

        $ = 6C \times 3$

        $ = 18C$ [From II equation, $C = 1\mu F$]

So,  $ = 18 \times 1\mu F$

       $ = 18\mu C$

$\therefore {q_2} = {C_2}{V_2}$

        $ = 3C \times 6$

        $ = 3 \times 1\mu F \times 6$

   $3volts$     $ = 18\mu C$

So, the charges on each capacitor is ${q_1} = {q_2} = 18\mu C$

When ${k_1}$ is open and ${k_2}$is closed then charge ${q_2}$ will be distributed among ${C_2}$and ${C_3}$. Let it be ${q_2}'$and ${q_3}$

$\therefore {q_2} = {q_2}' + {q_3}$

$18\mu C = 3 \times 1\mu F \times V + 3 \times 1\mu F \times V$

$18 = 6V$

$V = 3volts$

So the potential on ${C_2}$and ${C_3}$capacitors are  each

${q_2} = {C_2}V = 3 \times 1\mu F \times 3volt = 9\mu C$

${q_3} = {C_3}V = 3 \times 1\mu F \times 3volt = 9\mu C$

2.31 Calculate potential on the axis of a disc of radius $R$ due to a charge$Q$, uniformly distributed on its surface.

Ans: Consider a point $P$ on the axis perpendicular to the plane of disc and at a distance $x$ from the center $O$ of disc as shown in the figure.

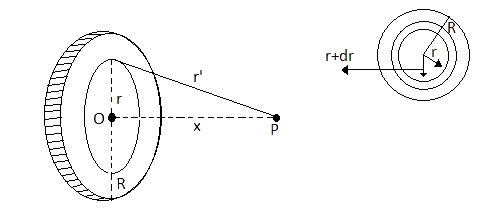
Now consider a ring of radius$r$, thickness $dr$and disc of radius$R$, as shown in figure. Let the charge on the ring be$dq$. 

The potential $dV$ due to the ring at P, will be

$dV = \dfrac{{kdq}}{{r'}}\left[ {\because r' = \sqrt {{r^2} + {x^2}} } \right]$

The charge on the ring is 

$dq = \sigma  \cdot area{\text{ of ring}}$

$dq = \sigma  \cdot \left[ {\pi {{\left( {r + dr} \right)}^2} - \pi {r^2}} \right]$

$dq = \sigma  \cdot \pi \left[ {{r^2} + d{r^2} + 2rdr - {r^2}} \right]$

As $dr$is very small, the value of $d{r^2}$will be negligible.

$\therefore dq = \sigma \pi \left( {2rdr} \right)$

   $dq = 2\pi r\sigma  \cdot dr$

$\therefore dV = \dfrac{{k \cdot 2\pi r\sigma dr}}{{\sqrt {\left( {{r^2} + {x^2}} \right)} }}$

So the potential due to the charged disc is

$\int\limits_0^V {dV}  = \int\limits_0^R {\dfrac{{k \cdot 2\pi r\sigma dr}}{{\sqrt {\left( {{r^2} + {x^2}} \right)} }}} $

$V = k \cdot 2\pi \sigma \int\limits_0^R {\dfrac{{rdr}}{{{{\left( {{r^2} + {x^2}} \right)}^{\dfrac{1}{2}}}}}} $

$V = 2\pi k\sigma \int\limits_0^R {r \cdot {{\left( {{r^2} + {x^2}} \right)}^{\dfrac{1}{2}}}dr} $

$V = 2\pi k\sigma \left[ {{{\left( {{R^2} + {x^2}} \right)}^{\dfrac{1}{2}}} - x} \right]$

$V = \dfrac{{2\pi \sigma }}{{4\pi {\varepsilon _0}}}\left[ {{{\left( {{R^2} + {x^2}} \right)}^{\dfrac{1}{2}}} - x} \right]$

$\because \pi {R^2}\sigma  = Q\left( {{\text{charge on disc}}} \right)$

$\sigma  = \dfrac{Q}{{\pi {R^2}}}$

$V = \dfrac{{2\pi {R^2}\sigma }}{{4\pi {\varepsilon _0}{R^2}}}\left[ {\sqrt {{R^2} + {x^2}}  - x} \right]$

$V = \dfrac{{2Q}}{{4\pi {\varepsilon _0}{R^2}}}\left[ {\sqrt {{R^2} + {x^2}}  - x} \right]$

2.32 Two charges ${q_1}$and ${q_2}$ are placed at $(0,0,d)$ and $(0,0, - d)$ respectively. Find the locus of points where the potential a zero.

Ans: Let the potential at any point $P(x,y,z)$ is zero then $ - {V_1} + {V_2} = 0$

$\dfrac{{k{q_1}}}{{\sqrt {{x^2} + {y^2} + {{(z - d)}^2}} }} + \dfrac{{k{q_2}}}{{\sqrt {{x^2} + {y^2} + {{(z + d)}^2}} }} = 0$

$\dfrac{{{q_1}}}{{\sqrt {{x^2} + {y^2} + {{(z - d)}^2}} }} + \dfrac{{{q_2}}}{{\sqrt {{x^2} + {y^2} + {{(z + d)}^2}} }} = 0$

$\dfrac{{{q_1}}}{{\sqrt {{x^2} + {y^2} + {{(z - d)}^2}} }} + \dfrac{{ - {q_2}}}{{\sqrt {{x^2} + {y^2} + {{(z + d)}^2}} }}$

$\dfrac{{{q_1}}}{{{q_2}}} = \dfrac{{ - \sqrt {{x^2} + {y^2} + {{(z - d)}^2}} }}{{\sqrt {{x^2} + {y^2} + {{(z + d)}^2}} }}$

$\dfrac{{{q_1}^2}}{{{q_2}^2}} = \dfrac{{{x^2} + {y^2} + {z^2} + {d^2} - zd}}{{{x^2} + {y^2} + {z^2} + {d^2} + zd}}$

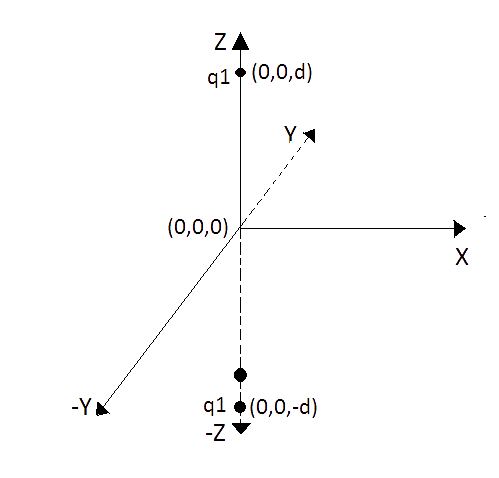
Componendo and dividend of $\dfrac{x}{a} = \dfrac{y}{b}$ is $\dfrac{{x + a}}{{x - a}} = \dfrac{{y + b}}{{y - b}}$

Then componendo and dividend of

$\dfrac{{{{\left( {\dfrac{{{q_1}}}{{{q_2}}}} \right)}^2}}}{1} = \dfrac{{{x^2} + {y^2} + {z^2} + {d^2} - 2zd}}{{{x^2} + {y^2} + {z^2} + {d^2} + 2zd}}$

$\dfrac{{{{\left( {\dfrac{{{q_1}}}{{{q_2}}}} \right)}^2} + 1}}{{{{\left( {\dfrac{{{q_1}}}{{{q_2}}}} \right)}^2} - 1}} = \dfrac{{{x^2} + {y^2} + {z^2} + {d^2} - 2zd + \left( {{x^2} + {y^2} + {z^2} + {d^2} + 2zd} \right)}}{{{x^2} + {y^2} + {z^2} + {d^2} - 2zd - \left( {{x^2} + {y^2} + {z^2} + {d^2} + 2zd} \right)}}$

$\left[ {\dfrac{{{{\left( {\dfrac{{{q_1}}}{{{q_2}}}} \right)}^2} + 1}}{{{{\left( {\dfrac{{{q_1}}}{{{q_2}}}} \right)}^2} - 1}}} \right] = \dfrac{{2\left( {{x^2} + {y^2} + {z^2} + {d^2}} \right)}}{{ - 4dz}}$

${x^2} + {y^2} + {z^2} + {d^2} =  - 2dz\left[ {\dfrac{{{{\left( {\dfrac{{{q_1}}}{{{q_2}}}} \right)}^2} + 1}}{{{{\left( {\dfrac{{{q_1}}}{{{q_2}}}} \right)}^2} - 1}}} \right]$

${x^2} + {y^2} + {z^2} = 2d\left[ {\dfrac{{{{\left( {\dfrac{{{q_1}}}{{{q_2}}}} \right)}^2} + 1}}{{{{\left( {\dfrac{{{q_1}}}{{{q_2}}}} \right)}^2} - 1}}} \right]z + {d^2} = 0$

\[{x^2} + {y^2} + {z^2} = 2d\left[ {\dfrac{{q_1^2 + q_2^2}}{{q_1^2 - q_2^2}}} \right]z + {d^2} = 0\]

This is the equation of sphere with center $(a,b,c)$ as required point is on $z - axis$so $a = 0$ , $b = 0$ and \[z = 2d\left[ {\dfrac{{q_1^2 + q_2^2}}{{q_1^2 - q_2^2}}} \right]\]

\[\left( {0,0, - 2d\left[ {\dfrac{{q_1^2 + q_2^2}}{{q_1^2 - q_2^2}}} \right]} \right)\]

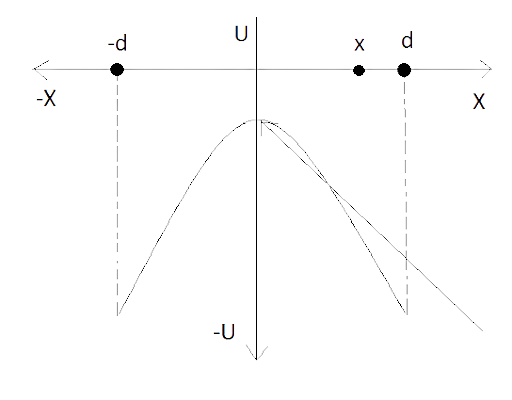
2.33 Two charges $ - q$ each are separated by distance$2d$. A third charge $ + q$ is kept at mid-point ‘O’. Find the potential energy of $ + q$ as a function of small distance $x$ from ‘O’ due to $ - q$ charges. Sketch P.E. v/s $x$ and convince yourself that the charge at O is in an unstable equilibrium.

Ans: $V = \dfrac{{kq}}{r}$

Let the equilibrium of $ + q$ is $P$at a distance $x$ from the mid-point of line joining two charges.

Force ${F_A}$ on $ + q$ is towards left side and force ${F_B}$ is towards right side, so for equilibrium of $ + q$ at $P$\[U = \dfrac{{k(q)( - q)}}{{(d - x)}} + \dfrac{{k(q)( - q)}}{{(d + x)}}\left( {\because U = \dfrac{{k{q_1}{q_2}}}{{{r_1}}}} \right)\],

${F_A} = {F_B}$

$\dfrac{{ - k{q^2}}}{{{{(d - x)}^2}}} = \dfrac{{ - k{q^2}}}{{{{(d + x)}^2}}}$

${(d - x)^2} = {(d + x)^2}$

$d - x = d + x$ (Taking square root)

$ - 2x = 0$

$x = 0$

So, Equilibrium position of charge $ + q$ between two $ - q$ charges is at mid-point (O) of line joining the two charges $ - q$ and$ - q$.

Now we have to find out potential energy of $ + q$ as a function of small distance $x$ from balance condition (O) towards any of $ - q$ charge.

Let new position of charge $ + q$ from a small distance $x$ from (O)

\[U =  - k{q^2}\left[ {\dfrac{1}{{(d - x)}} + \dfrac{1}{{(d + x)}}} \right]\]

\[U =  - k{q^2}\left[ {\dfrac{{d + x + d - x}}{{(d - x)(d + x)}}} \right] =  - k{q^2}\left[ {\dfrac{{2d}}{{{d^2} - {x^2}}}} \right]\]$U$$x$\[U = \dfrac{{ - {q^2}}}{{4\pi {\varepsilon _0}}} \cdot \dfrac{{2d}}{{({d^2} - {x^2})}}\]

So, is the P.E. as a function of.

Class 12 Physics - Electrostatic Potential and Capacitance

Vedantu's NCERT exemplar for Class 12 Physics Chapter 2 can give significant benefits to students. It will provide students with a thorough theoretical understanding of this chapter, allowing them to answer the problems on their own, while also developing confidence to face all different types of questions that may appear. Experts enlist, describe, and explain the list of the important questions, which includes questions that are frequently asked in tests.

First and foremost, begin reading NCERT thoroughly. You should practice every question in the book. Divide the chapter into separate themes and headers to make notes. Make a list of important derivations and formulae, for example, Capacitors in series, Capacitors in parallel, and the Gauss theorem. Go over the chapter's synopsis or look over the notes. Complete chapter tests and worksheets. Try practising with the NCERT Exemplar. Make a list of your questions and have them answered. This might be enough. Also, examine the various types of possible questions. The three keys to perfecting your performance are - prepare, practice, and sample tests.