NCERT Exemplar for Class 12 Maths Chapter-11 (Book Solutions)

Solved Examples

Short Answers Questions

1. If the direction ratios of a line are 1, 1, 2, find the direction cosines of the line.

Ans: The direction cosines are given by,

$l=\frac{a}{\sqrt{{{a}^{2}}~+~{{b}^{2}}~+~{{c}^{2}}}},~m=\frac{b}{\sqrt{{{a}^{2}}~+~{{b}^{2}}~+~{{c}^{2}}}},~n=\frac{c}{\sqrt{{{a}^{2}}~+~{{b}^{2}}~+~{{c}^{2}}}}$

Here a = 1, b = 1, and c = 2,

Therefore $l=\frac{1}{\sqrt{{{1}^{2}}~+~{{1}^{2}}~+~{{2}^{2}}}},~m=\frac{1}{\sqrt{{{1}^{2}}~+~{{1}^{2}}~+~{{2}^{2}}}},~n=\frac{2}{\sqrt{{{1}^{2}}~+~{{1}^{2}}~+~{{2}^{2}}}}$

 $l=\frac{1}{\sqrt{1~+~1~+~4}},~m=\frac{1}{\sqrt{1~+~1~+~4}},~n=\frac{2}{\sqrt{1~+~1~+~4}}$

 $l=\frac{1}{\sqrt{6}},~m=\frac{1}{\sqrt{6}},~n=\frac{2}{\sqrt{6}}$

Hence $\pm \left( \frac{1}{\sqrt{6}},~\frac{1}{\sqrt{6}},~\frac{2}{\sqrt{6}} \right)$ are the direction cosines of the lines.

2. Find the direction cosines of the line passing through the points P (2, 3, 5) and Q (–1, 2, 4).

Ans: The cosines of a line passing through the points $P\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)$ and $Q\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)$ are,

 $\frac{{{x}_{2}}~-~{{x}_{1}}}{PQ},~\frac{{{y}_{2}}~-~{{y}_{1}}}{PQ},~\frac{{{z}_{2}}~-~{{z}_{1}}}{PQ}$

Here $PQ=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}+{{({{z}_{2}}-{{z}_{1}})}^{2}}}$

 $PQ=\sqrt{{{(-1-2)}^{2}}+{{(2-3)}^{2}}+{{(4-5)}^{2}}}$

 $PQ=\sqrt{{{(3)}^{2}}+{{(-1)}^{2}}+{{(-1)}^{2}}}$

 $PQ=\sqrt{9+1+1}$

 $PQ=\sqrt{11}$

Here direction cosines are,

 $\pm \left( \frac{-1~-~2}{\sqrt{11}},~\frac{2~-~3}{\sqrt{11}},~\frac{4~-~5}{\sqrt{11}} \right)$

 $\pm \left( \frac{-3}{\sqrt{11}},~\frac{-1}{\sqrt{11}},~\frac{-1}{\sqrt{11}} \right)$

OR

 $\pm \left( \frac{3}{\sqrt{11}},~\frac{1}{\sqrt{11}},~\frac{1}{\sqrt{11}} \right)$

3. If a line makes an angle of 30°, 60°, 90° with the positive direction of x, y, z-axis, respectively, then find its cosines.

Ans: cosα, cosβ, cosγ are the direction cosines of a line that makes an angle of α, β, γ with the axis.

cosα = cos 30° = $\frac{\sqrt{3}}{2}$

cosβ = cos 60° = $\frac{1}{2}$

cosγ = cos 90° = 0

As a result, the line's Direction Cosines are cos 30°, cos 60°, cos 90° i.e., $\pm \left( \frac{\sqrt{3}}{2},~\frac{1}{2},~0 \right)$

4. The x-coordinate of a point on the line joining the points Q (2, 2, 1) and R (5, 1, –2) is 4. Find its z-coordinate.

Ans: Given $\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)=\left( 2,2,1 \right)$ and $\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)=\left( 5,1,-2 \right)$

If the point P divides QR in λ : 1 ratio, the coordinates of P are

 $QR=\left( \frac{\lambda {{x}_{2}}~+~1{{x}_{1}}}{\lambda ~+~1},\frac{\lambda {{y}_{2}}~+~1{{y}_{1}}}{\lambda ~+~1},\frac{\lambda {{z}_{2}}~+~1{{z}_{1}}}{\lambda ~+~1} \right)$

 $QR=\left( \frac{\lambda \left( 5 \right)~+~2}{\lambda ~+~1},\frac{\lambda \left( 1 \right)~+~2}{\lambda ~+~1},\frac{\lambda \left( -2 \right)~+~1}{\lambda ~+~1} \right)$

 $QR=\left( \frac{5\lambda ~+~2}{\lambda ~+~1},\frac{\lambda ~+~2}{\lambda ~+~1},\frac{-2\lambda ~+~1}{\lambda ~+~1} \right)$

Since x-coordinate = X = 4, then

 $X=\frac{5\lambda ~+~2}{\lambda ~+~1}$

 $4=\frac{5\lambda ~+~2}{\lambda ~+~1}$

 $4\lambda +4=5\lambda +2$

 $5\lambda -4\lambda =4-2$

 $\lambda =2$

Hence the z-coordinate of P = $\frac{-2\lambda ~+~1}{\lambda ~+~1}$

On substituting the value λ = 2, we get 

 $P=\frac{-2\left( 2 \right)~+~1}{2~+~1}$

 $P=\frac{-4~+~1}{2~+~1}$

 $P=\frac{-3}{3}$

 $P=~-1$

5. Find the distance of the point whose position vector is $\left( 2\hat{i}+\hat{j}-\hat{k} \right)$ from the plane $\underset{\scriptscriptstyle-}{r}\cdot \left( \hat{i}-2\hat{j}+4\hat{k} \right)=9$

Ans: Here $\underset{\scriptscriptstyle-}{a}=2\hat{i}+\hat{j}-\hat{k}$, $\underset{\scriptscriptstyle-}{n}=\hat{i}-2\hat{j}+4\hat{k}$ and $d=9$

So, Distance = $\frac{\left( \underset{\scriptscriptstyle-}{a}~\cdot ~\underset{\scriptscriptstyle-}{n} \right)~-~d}{\left| ~\underset{\scriptscriptstyle-}{n}~ \right|}$

Distance = $\frac{\left| ~\left( 2\hat{i}~+~\hat{j}~-~\hat{k} \right)\cdot ~\left( \hat{i}~-~2\hat{j}~+~4\hat{k} \right)~-~9~ \right|}{\sqrt{{{1}^{2}}~+~{{(-2)}^{2}}~+~{{4}^{2}}}}$

Distance = $\frac{\left| ~2~-~2~-~4~-~9~ \right|}{\sqrt{1~+~4~+~16}}$

Distance = $\frac{13}{\sqrt{21}}$units

6. Find the distance of the point (–2, 4, –5) from the line $\frac{x~+~3}{3}=\frac{y~-~4}{5}=\frac{z~+~8}{6}$

Ans: 

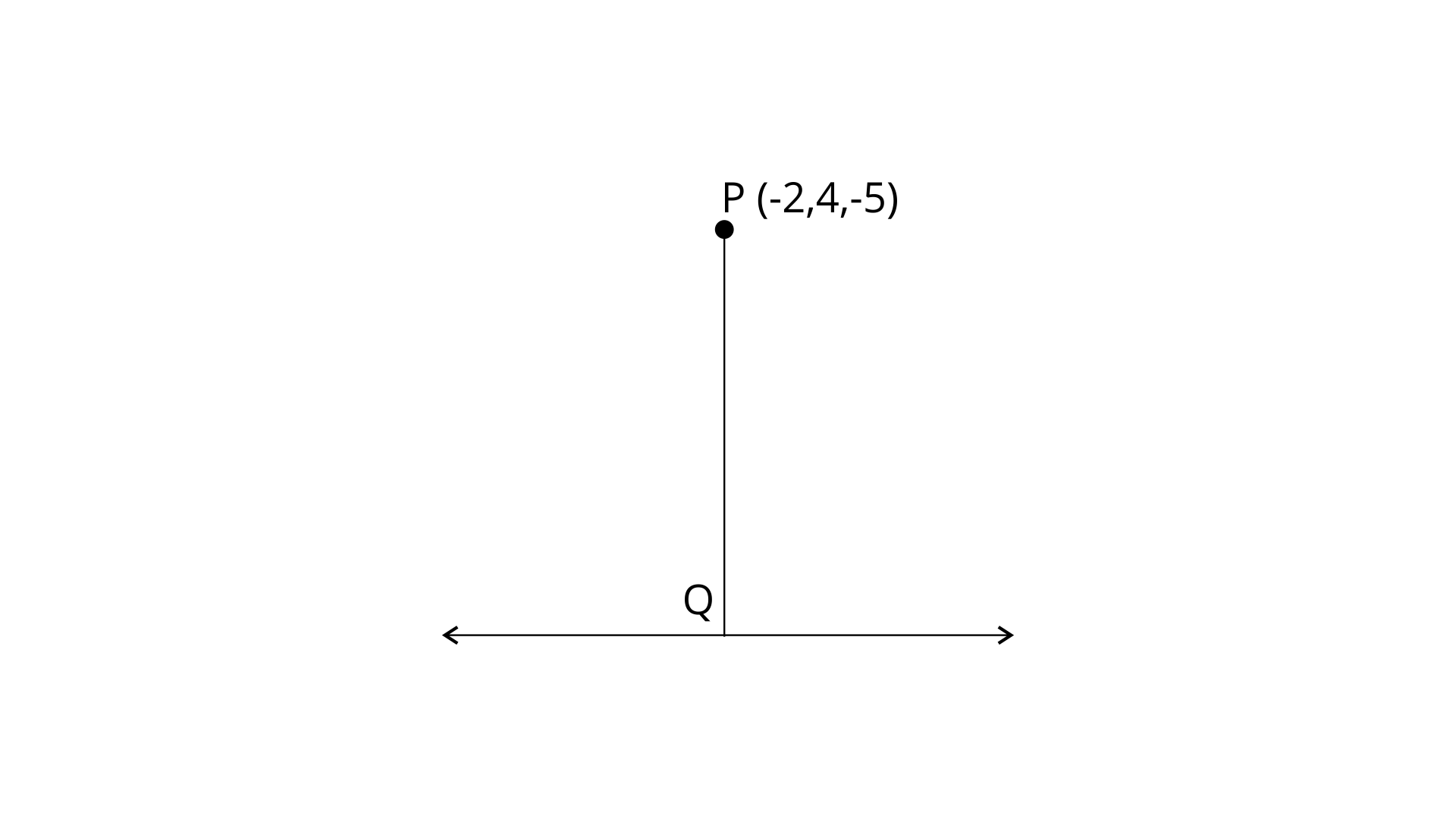
Given $\frac{x~+~3}{3}=\frac{y~-~4}{5}=\frac{z~+~8}{6}$

On equating the above equation to ‘t’, we get

 $\frac{x~+~3}{3}=\frac{y~-~4}{5}=\frac{z~+~8}{6}=\lambda $

Therefore, 

$\frac{x~+~3}{3}=\lambda $   $\Rightarrow $   $x=3\lambda -3$

$\frac{y~-~4}{5}=\lambda $   $\Rightarrow $   $y=5\lambda +4$

$\frac{z~+~8}{6}=\lambda $   $\Rightarrow $   $z=6\lambda -8$

Hence the points on the given line are Q(3$\lambda $ – 3, 5$\lambda $ + 4, 6$\lambda $ – 8) and P(–2. 4. –5)

Direction ratio of $PQ=3\lambda -3+2,~5\lambda +4-4,~6\lambda -8+5$

 $\underline{PQ}=\left( 3\lambda -1 \right)~\hat{i},~5\lambda \widehat{~j},~\left( 6\lambda -3 \right)\widehat{~k}$

Since PQ is perpendicular to the line $3\hat{i}+5\hat{j}+6\hat{k}$, then

 $3\left( 3\lambda -1 \right)+5\left( 5\lambda  \right)+6\left( 6\lambda -3 \right)=0$

 $9\lambda -3+25\lambda +36\lambda -18=0$

 $9\lambda +25\lambda +36\lambda =18+3$

 $70\lambda =21$

 $\lambda =\frac{21}{70}$

 $\lambda =\frac{3}{10}$

Thus $\underline{PQ}=\left( 3\left( \frac{3}{10} \right)-1 \right)~\hat{i},~5\left( \frac{3}{10} \right)~\hat{j},~\left( 6\left( \frac{3}{10} \right)-3 \right)~\hat{k}$

 $\underline{PQ}=\left( \frac{9}{10}-1 \right)~\hat{i},~\frac{15}{10}~~\hat{j},~\left( \frac{18}{10}-3 \right)~\hat{k}$

 $\underline{PQ}=\left( \frac{9~-~10}{10} \right)~\hat{i},~\frac{15}{10}~\hat{j},~\left( \frac{18~-~30}{10} \right)~\hat{k}$

 $\underline{PQ}=\frac{-1}{10}~\hat{i},~\frac{15}{10}~\hat{j},~\frac{12}{10}~\hat{k}$

 $\left| ~\underline{PQ}~ \right|=\sqrt{{{(\frac{1}{10})}^{2}}+{{(\frac{15}{10})}^{2}}+{{(\frac{12}{10})}^{2}}}$

 $\left| ~\underline{PQ}~ \right|=\sqrt{\frac{1}{100}+\frac{225}{100}+\frac{144}{100}}$

 $\left| ~\underline{PQ}~ \right|=\sqrt{\frac{1~+~225~+~144}{100}}$

 $\left| ~\underline{PQ}~ \right|=\sqrt{\frac{370}{100}}$

 $\left| ~\underline{PQ}~ \right|=\sqrt{\frac{37}{10}}$

7. Find the coordinates of the point where the line through (3, –4, –5) and (2, –3, 1) crosses the plane passing through three points (2, 2, 1), (3, 0, 1) and (4, –1, 0).

Ans: The equation of the plane through three points (2, 2, 1), (3, 0, 1), and (4, –1, 0) is

$\left| \begin{matrix} x-2 & y-2 & z-1  \\ x-3 & y-0 & z-1  \\ x-4 & y+1 & z-0  \\ \end{matrix} \right|=0$ 

By using elementary row operations ${{R}_{2}}\to {{R}_{1}}-{{R}_{2}}$ and ${{R}_{3}}\to {{R}_{1}}-{{R}_{3}}$ we get,

$\left| \begin{matrix}x-2 & y-2 & z-1  \\3-2 & 0-2 & 0  \\4-2 & -1-2 & -1  \\\end{matrix} \right|=0$

$\left| \begin{matrix} x-2 & y-2 & z-1  \\1 & -2 & 0  \\2 & -3 & -1  \\\end{matrix} \right|=0$

On solving the above determinant we get,

(x – 2)(2 – 0) – (y – 2)(–1 + 0) + (z – 1)(–3 + 4) = 0

(2x – 4) – (–y + 2) + (z – 1) = 0

2x – 4 + y – 2 + z – 1 = 0

2x + y + z – 7 = 0

2x + y + z = 7

Now the equation of the line through (3, –4, –5) and (2, –3, 1) is,

 $\frac{x~-~3}{2~-~3}=\frac{y~+~4}{-3~+~4}=\frac{z~+~5}{1~+~5}=\lambda $

 $\frac{x~-~3}{-1}=\frac{y~+~4}{1}=\frac{z~+~5}{6}=\lambda $

On equating each term to $\lambda $ we get,

 $\frac{x~-~3}{-1}=\lambda ~~~~\Rightarrow ~~~~x=\left( -\lambda +3 \right)$

 $\frac{y~+~4}{1}=\lambda ~~~~\Rightarrow ~~~~y=\left( \lambda -4 \right)$

 $\frac{z~+~5}{6}=\lambda ~~~~\Rightarrow ~~~~z=\left( 6\lambda -5 \right)$

The above points satisfy the plane equation $2x+y+z=7$ at the point of intersection,

Now substituting the value of $x,~y$ and $z$ in the equation of the plane, we get

 $2\left( -\lambda +3 \right)+\left( \lambda -4 \right)+\left( 6\lambda -5 \right)=7$

 $-2\lambda +6+\lambda -4+6\lambda -5=7$

 $-2\lambda +\lambda +6\lambda =7+5+4-6$

 $-2\lambda +\lambda +6\lambda =7+5+4-6$

 $5\lambda =10$

 $\lambda =\frac{10}{5}$

 $\lambda =2$

Thus the point of intersection is $P\left( 1,-2,~7 \right)$

Long Answers Questions

8. Find the distance of the point (–1, –5, – 10) from the point of intersection of the line $\underset{\scriptscriptstyle-}{r}=2\hat{i}-\hat{j}+2\hat{k}+\lambda \left( 3\hat{i}+4\hat{j}+2\hat{k} \right)$ and the plane $\underset{\scriptscriptstyle-}{r}\cdot \left( \hat{i}-\hat{j}+\hat{k} \right)=5$.

Ans: Given equation of the line is $\underset{\scriptscriptstyle-}{r}=2\hat{i}-\hat{j}+2\hat{k}+\lambda \left( 3\hat{i}+4\hat{j}+2\hat{k} \right)$------ (1)

Equation of the plane is $\underset{\scriptscriptstyle-}{r}\cdot \left( \hat{i}-\hat{j}+\hat{k} \right)=5$ ------ (2)

Now substitute the value of $\underset{\scriptscriptstyle-}{r}$ in equation (2) to find the point of intersection of the line and plane.

 $2\hat{i}-\hat{j}+2\hat{k}+\lambda \left( 3\hat{i}+4\hat{j}+2\hat{k} \right)\cdot \left( \hat{i}-\hat{j}+\hat{k} \right)=5$

 $\left( 2\hat{i}-\hat{j}+2\hat{k}+3\lambda \hat{i}+4\lambda \hat{j}+2\lambda \hat{k} \right)\cdot \left( \hat{i}-\hat{j}+\hat{k} \right)=5$

 $\left[ \left( 2+3\lambda  \right)~\hat{i}+\left( -1+4\lambda  \right)~\hat{j}+\left( 2+2\lambda  \right)~\hat{k}~ \right]\cdot \left( \hat{i}-\hat{j}+\hat{k} \right)=5$

 $\left[ \left( 2+3\lambda  \right)\left( ~\hat{i}\cdot \hat{i}~ \right)+\left( -1+4\lambda  \right)\left( ~\hat{j}\cdot \left( -\hat{j}~ \right) \right)+\left( 2+2\lambda  \right)\left( ~\hat{k}\cdot \hat{k}~ \right) \right]=5$

We know that $~\hat{i}\cdot \hat{i}~=1$ hence,

 $\left( 2+3\lambda  \right)\left( 1 \right)+\left( -1+4\lambda  \right)\left( -1 \right)+\left( 2+2\lambda  \right)\left( 1 \right)=5$

 $2+3\lambda +1-4\lambda +2+2\lambda =5$

 $3\lambda -4\lambda +2\lambda =5-2-1-2$

 $5\lambda -4\lambda =5-5$

 $\lambda =0$

So the equation of the line is,

 $\underset{\scriptscriptstyle-}{r}=2\hat{i}-\hat{j}+2\hat{k}+\lambda \left( 3\hat{i}+4\hat{j}+2\hat{k} \right)$

$\underset{\scriptscriptstyle-}{r}=2\hat{i}-\hat{j}+2\hat{k}$   (because $\lambda =0$)

Consider the point of intersection to be (x, y, z)

So, $\underset{\scriptscriptstyle-}{r}=x\hat{i}+y\hat{j}+z\hat{k}$

 $x\hat{i}+y\hat{j}+z\hat{k}=2\hat{i}-\hat{j}+2\hat{k}$

Thus $x=2,~y=-1,~z=2$

Therefore the point of intersection is (2, –1, 2).

Distance between point (2, –1, 2) and (–1, –5, – 10) is

 $\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}+{{({{z}_{2}}-{{z}_{1}})}^{2}}}$

 $\sqrt{{{(-1-2)}^{2}}+{{(-5-\left( -1 \right))}^{2}}+{{(-10-2)}^{2}}}$

 $\sqrt{{{(-3)}^{2}}+{{(-4)}^{2}}+{{(-12)}^{2}}}$

 $\sqrt{9+16+144}$

 $\sqrt{169}$ $13$units

9. A plane meets the coordinate axis in A, B, C such that the centroid of the ∆ABC is the point (α, β, γ). Show that the equation of the plane is $\frac{x}{\alpha }+\frac{y}{\beta }+\frac{z}{\gamma }=3$.

Ans: Let the equation of the plane be $\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$

Then the coordinates of $A,~B$ and $C$ be $\left( a,0,0 \right),~\left( 0,b,0 \right)$ and $\left( 0,0,c \right)$ respectively.

Hence centroid of $\Delta $ABC is,

 $\left( \frac{{{x}_{1}}~+~{{x}_{2}}~+~{{x}_{3}}}{3},\frac{{{y}_{1}}~+~{{y}_{2}}~+~{{y}_{3}}}{3},\frac{{{z}_{1}}~+~{{z}_{2}}~+~{{z}_{3}}}{3} \right)$

 $\left( \frac{a~+~0~+~0}{3},\frac{0~+~b~+~0}{3},\frac{0~+~0~+~c}{3} \right)$

 $\left( \frac{a}{3},\frac{b}{3},\frac{c}{3} \right)$

But $\frac{a}{3}=\alpha $, $\frac{b}{3}=\beta $ and $\frac{c}{3}=\gamma $ because the centroid of $\Delta $ABC are $\left( \alpha ,\beta ,\gamma  \right)$ as given in the question.

∴$a=3\alpha $, $b=3\beta $ and $c=3\gamma $

Thus equation of the plane is

 $\frac{x}{3\alpha }+\frac{y}{3\beta }+\frac{z}{3\gamma }=1$

 $\frac{x}{\alpha }+\frac{y}{\beta }+\frac{z}{\gamma }=3$

10. Find the angle between the lines whose direction cosines are given by the equations: $\text{3l+m+5n=0}$ and $\text{6mn-2nl+5lm=0}$.

Ans: Given equations:

$3l+m+5n=0$ ------ (1)

$6mn-2nl+5lm=0$ ------ (2)

From equation (1) we get $m=\left( -3l-5n \right)$

Substituting the value of $m$ in equation (2), we get

 $6n\left( -3l-5n \right)-2nl+5l\left( -3l-5n \right)=0$

 $-18ln-30{{n}^{2}}-2nl-15{{l}^{2}}-25ln=0$

$-15{{l}^{2}}-30{{n}^{2}}-45ln=0$ ------ $\div \left( -15 \right)$

 ${{l}^{2}}+2{{n}^{2}}+3ln=0$

 $\left( l+2n \right)\left( l+n \right)=0$

$\left( l+2n \right)=0$   or   $\left( l+n \right)=0$ 

$l=~-2n$   or   $l=~-n$

If $l=~-2n$  then

 $3\left( -2n \right)+m+5n=0$

 $-6n+m+5n=0$

 $-n+m=0$

 $m=n$

If $l=~-n$  

 $3\left( -n \right)+m+5n=0$

 $-3n+m+5n=0$

 $2n+m=0$

 $m=~-2n$

As a result, the direction ratios of two lines are proportional to $-n,-2n,n$ and $-2n,n,n$.

That is 1, 2, –1 and –2, 1, 1

So the vectors are parallel to the lines are

 $\underset{\scriptscriptstyle-}{a}=\hat{i}+2\hat{j}-\hat{k}$

And  $\underset{\scriptscriptstyle-}{b}=~-2\hat{i}+\hat{j}+\hat{k}$

If $\theta $ is the angle between the lines, then

 $cos~\theta =\frac{\underset{\scriptscriptstyle-}{a}~\underset{\scriptscriptstyle-}{b}}{\left| ~\underset{\scriptscriptstyle-}{a}~\left| ~ \right|~\underset{\scriptscriptstyle-}{b}~ \right|}$

 $cos~\theta =\frac{\left( \hat{i}+2\hat{j}-\hat{k} \right)~\cdot ~\left( -2\hat{i}+\hat{j}+\hat{k} \right)}{\sqrt{{{1}^{2}}~+~{{2}^{2}}~+~{{(-1)}^{2}}}~\sqrt{{{\left( -2 \right)}^{2}}~+~{{1}^{2}}~+~{{1}^{2}}}}$

 $cos~\theta =\frac{\left( -2 \right)\left( 1 \right)~+~2\left( 1 \right)~+~\left( -1 \right)\left( -1 \right)}{\sqrt{1~+~4~+~1}~\sqrt{4~+~1~+~1}}$

 $cos~\theta =\frac{-2~+~2~+~1}{\sqrt{6}~\sqrt{6}}$

 $cos~\theta =\frac{1}{6}$

 $\theta =co{{s}^{-1}}\left( \frac{1}{6} \right)$

11. Find the coordinates of the foot of the perpendicular drawn from the point A (1, 8, 4) to the line joining the points B (0, –1, 3) and C (2, –3, –1).

Ans: Let L be the perpendicular foot drawn from points A (1, 8, 4) to the line passing through B (0, –1, 3) and C (2, –3, –1) as shown in the figure. The equation of line BC using the formula $\underset{\scriptscriptstyle-}{r}=a+\lambda \left( b-a \right)$ is,

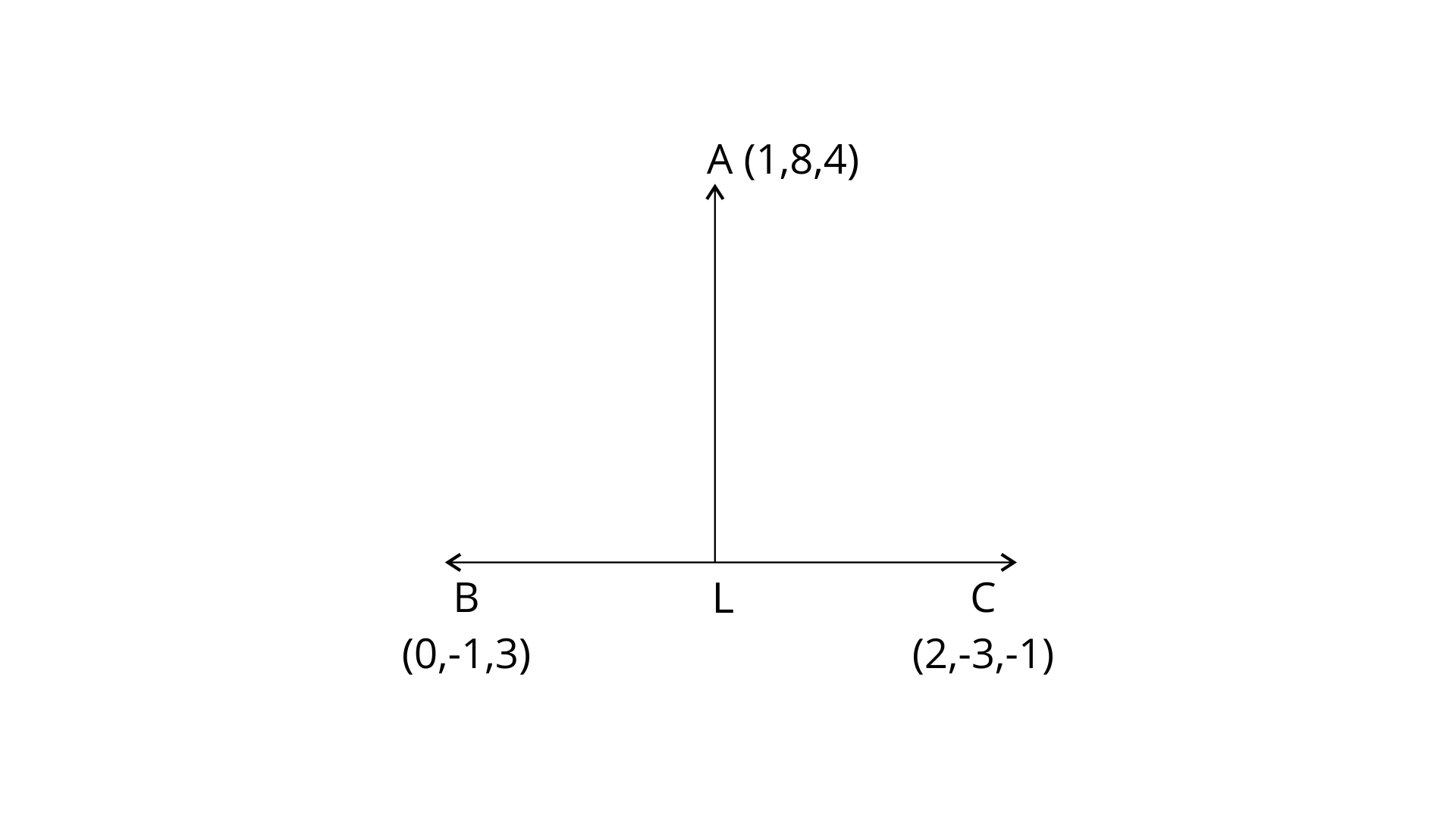
 $\underset{\scriptscriptstyle-}{r}=\left( -\hat{j}+3\hat{k} \right)+\lambda \left( -\hat{j}+3\hat{k}-\left( 2\hat{i}-3\hat{j}-\hat{k} \right) \right)$

 $\underset{\scriptscriptstyle-}{r}=\left( -\hat{j}+3\hat{k} \right)+\lambda \left( 2\hat{i}-2\hat{j}-4\hat{k} \right)$

 $\underset{\scriptscriptstyle-}{r}=\left( -\hat{j}+3\hat{k} \right)+\left( 2\lambda \hat{i}-2\lambda \hat{j}-4\lambda \hat{k} \right)$

 $\underset{\scriptscriptstyle-}{r}=2\lambda \hat{i}-\left( 1+2\lambda  \right)\hat{j}+\left( 3-4\lambda  \right)\hat{k}$

 $\underset{\scriptscriptstyle-}{r}=2\lambda \hat{i}-\left( 1+2\lambda  \right)\hat{j}+\left( 3-4\lambda  \right)\hat{k}$

Consider the point of intersection to be $\left( x,y,z \right)$

So, $\underset{\scriptscriptstyle-}{r}=x\hat{i}+y\hat{j}+z\hat{k}$

 $x\hat{i}+y\hat{j}+z\hat{k}=2\lambda \hat{i}-\left( 1+2\lambda  \right)\hat{j}+\left( 3-4\lambda  \right)\hat{k}$

 $x=2\lambda ,~y=-\left( 1+2\lambda  \right),~z=\left( 3-4\lambda  \right)$

Hence the coordinates of L are $\left( 2\lambda ,~-1-2\lambda ,~3-4\lambda  \right)$

Therefore the direction ratio of the line AL are proportional to

$2\lambda -1,-2\lambda -1-8,-4\lambda +3-4$ 

Or

 $2\lambda -1,-2\lambda -9,-4\lambda -1$

Direction ratios of the given lines are proportional to 2, –2, –4, as AL is perpendicular to the lines

 $2\times \left( 2\lambda -1 \right)+\left( -2 \right)\left( -2\lambda -9 \right)+\left( -4 \right)\left( -4\lambda -1 \right)=0$

 $4\lambda -2+4\lambda +18+16\lambda +4=0$

 $4\lambda +4\lambda +16\lambda =-4-18+2$

 $24\lambda =20$

 $\lambda =\frac{-20}{24}$

 $\lambda =-\frac{5}{6}$

Substitute $\lambda =-\frac{5}{6}$ in $\left( 2\lambda ,-2\lambda -1,-4\lambda +3 \right)$

 $\left( 2\left( -\frac{5}{6} \right),-2\left( -\frac{5}{6} \right)-1,-4\left( -\frac{5}{6} \right)+3 \right)$

 $\left( -\frac{5}{3},\frac{5}{3}-1,\frac{10}{3}+3 \right)$

 $\left( -\frac{5}{3},\frac{5~-~3}{3},\frac{10~+~3}{3} \right)$

 $\left( -\frac{5}{3},\frac{2}{3},\frac{13}{3} \right)$

Thus the coordinates of the foot of the perpendicular are $\left( -\frac{5}{3},\frac{2}{3},\frac{13}{3} \right)$

12. Find the image of the point (1, 6, 3) in the line $\frac{x}{1}=\frac{y~-~1}{2}=\frac{z~-~2}{3}$.

Ans: Let P (1, 6, 3) represent the given point and L represent the foot of the perpendicular from P to the given line.

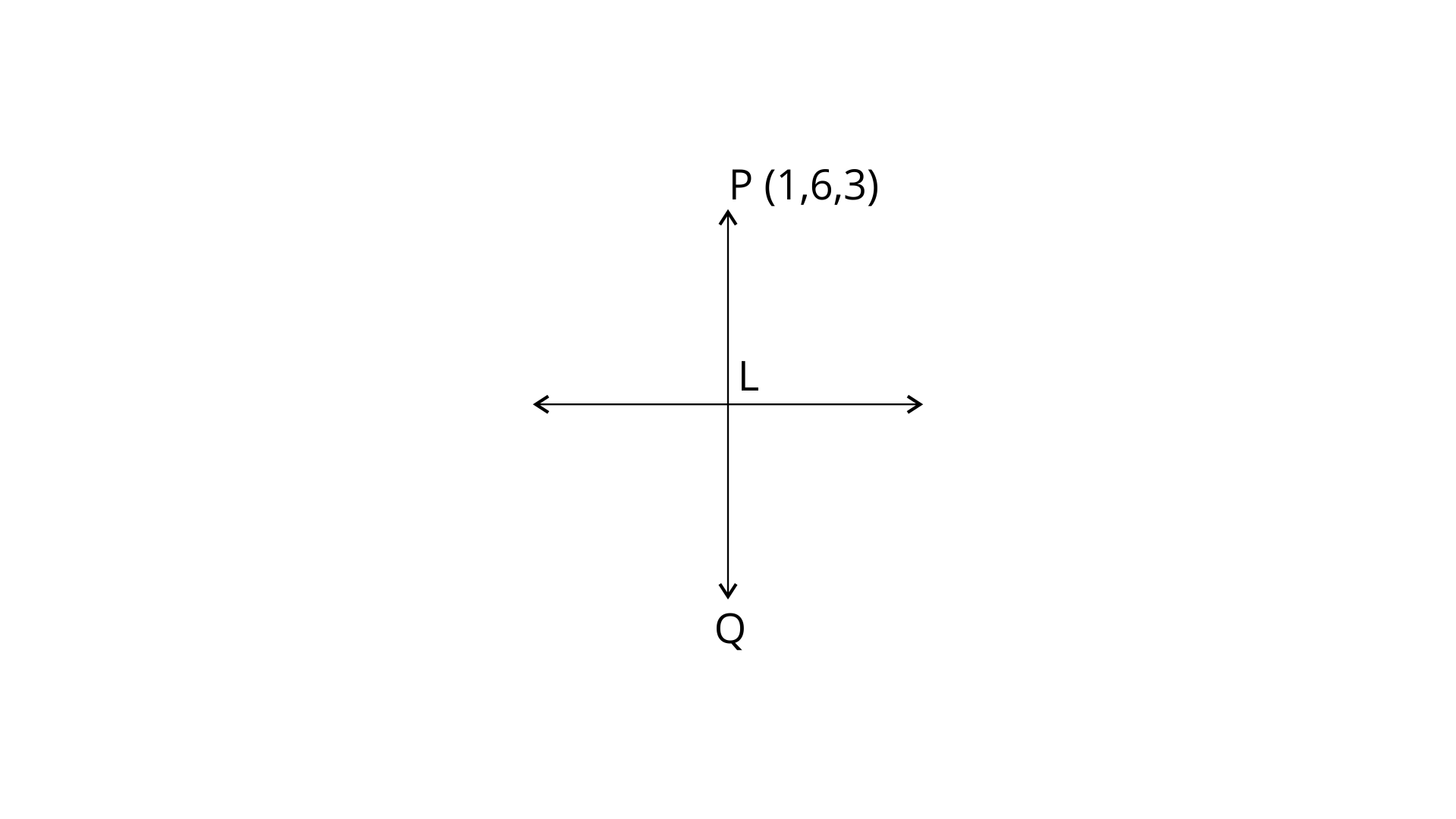
The coordinates of a general point on a given line are:

 $\frac{x~-~0}{1}=\frac{y~-~1}{2}=\frac{z~-~2}{3}=\lambda $

Thus,

 $x=\lambda $

 $y=2\lambda +1$

 $z=3\lambda +2$

If the coordinates of L are (λ, 2λ + 1, 3λ + 2), then the direction ratios of PL are λ – 1, 2λ – 5, 3λ – 1.

Since direction ratio of the line is perpendicular to PL are 1, 2, 3

 $\left( \lambda -1 \right)1+\left( 2\lambda -5 \right)2+\left( 3\lambda -1 \right)3=0$

 $\lambda -1+4\lambda -10+9\lambda -3=0$

 $\lambda +4\lambda +9\lambda =3+10+1$

 $14\lambda =14$

 $\lambda =1$

Hence coordinates of L are (1, 3, 5)

Let $Q\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)$ be the image of P(1, 6, 3) in the given line. Then L is the midpoint of PQ.

∴ $\frac{{{x}_{1}}~+~1}{2}=1,~\frac{{{y}_{1}}~+~6}{2}=3,~\frac{{{z}_{1}}~+~3}{2}=5$

${{x}_{1}}=2-1$,  ${{y}_{1}}=6-6$,  ${{z}_{1}}=10-3$

${{x}_{1}}=1$,  ${{y}_{1}}=0$,  ${{z}_{1}}=7$

Hence the image of (1, 6, 3) in the given line is (1, 0, 7)

13. Find the image of the point having position vector $\hat{i}+3\hat{j}+4\hat{k}$ in the plane $\underset{\scriptscriptstyle-}{r}\cdot \left( 2\hat{i}-\hat{j}+\hat{k}~ \right)+3=0$

Ans: Let $P=\hat{i}+3\hat{j}+4\hat{k}$ and Q be the image of P in the given plane $\underset{\scriptscriptstyle-}{r}\cdot \left( 2\hat{i}-\hat{j}+\hat{k}~ \right)+3=0$.

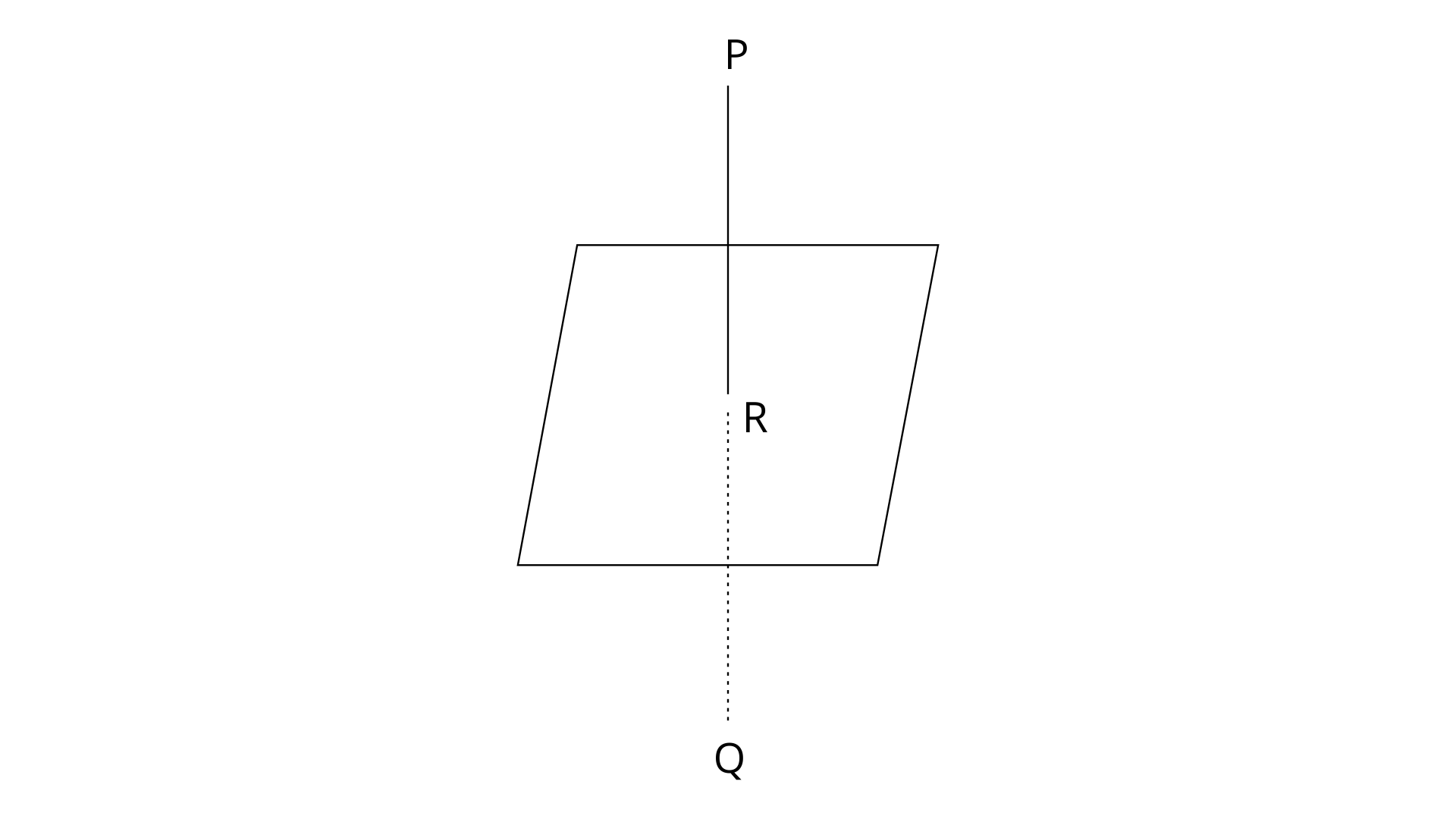
Since PQ passes through P and is normal to the given plane, the equation for PQ is,

 $\underset{\scriptscriptstyle-}{r}=\left( \hat{i}+3\hat{j}+4\hat{k} \right)+\lambda \left( 2\hat{i}-\hat{j}+\hat{k}~ \right)$

Because Q is on the line PQ. its position vector can be expressed as, 

 $\left( \hat{i}+3\hat{j}+4\hat{k} \right)+\lambda \left( 2\hat{i}-\hat{j}+\hat{k}~ \right)$

 $\left( \hat{i}+3\hat{j}+4\hat{k} \right)+\left( 2\lambda \hat{i}-\lambda \hat{j}+\lambda \hat{k}~ \right)$

 $\left( 1+2\lambda  \right)\hat{i}+\left( 3-\lambda  \right)\hat{j}+\left( 4+\lambda  \right)\hat{k}$

Since R is the midpoint of PQ, the position vector of R is,

 $\frac{\left[ \left( 1~+~2\lambda  \right)\hat{i}~+~\left( 3~-~\lambda  \right)\hat{j}~+~\left( 4~+~\lambda  \right)\hat{k}~\left] ~+~ \right[\hat{i}+3\hat{j}+4\hat{k}~ \right]}{2}$

 $\frac{\left( \hat{i}~+~2\lambda \hat{i}~+~\hat{i}~ \right)~+~\left( 3\hat{j}~-~\lambda \hat{j}~+~3\hat{j}~ \right)~+~\left( 4\hat{k}~+~\lambda \hat{k}~+~4\hat{k}~ \right)}{2}$

 $\frac{2\hat{i}\left( 1~+~\lambda  \right)~+~\hat{j}\left( 6~-~\lambda  \right)~+~\hat{k}\left( 8~+~\lambda  \right)}{2}$

 $\frac{2\hat{i}\left( 1~+~\lambda  \right)~}{2}+\frac{\hat{j}\left( 6~-~\lambda  \right)~}{2}+\frac{\hat{k}\left( 8~+~\lambda  \right)}{2}$

 $\left( \lambda +1 \right)\hat{i}+\left( 3-\frac{\lambda }{2} \right)\hat{j}+\left( 4+\frac{\lambda }{2} \right)\hat{k}$

Since R lies on the point  $\underset{\scriptscriptstyle-}{r}\cdot \left( 2\hat{i}-\hat{j}+\hat{k}~ \right)+3=0$, we get

 $\left[ \left( \lambda +1 \right)\hat{i}+\left( 3-\frac{\lambda }{2} \right)\hat{j}+\left( 4+\frac{\lambda }{2} \right)\hat{k} \right]\cdot \left( 2\hat{i}-\hat{j}+\hat{k}~ \right)+3=0$

 $\left( \lambda +1 \right)\hat{i}\cdot 2\hat{i}+\left( 3-\frac{\lambda }{2} \right)\hat{j}\cdot \left( -\hat{j} \right)+\left( 4+\frac{\lambda }{2} \right)\hat{k}\cdot \hat{k}~+3=0$

 $\left( \lambda +1 \right)2+\left( 3-\frac{\lambda }{2} \right)\left( -1 \right)+\left( 4+\frac{\lambda }{2} \right)\left( 1 \right)+3=0$

 $2\lambda +2-3+\frac{\lambda }{2}+4+\frac{\lambda }{2}+3=0$

 $2\lambda +\frac{\lambda }{2}+\frac{\lambda }{2}=-4-2$

 $\frac{4\lambda ~+~\lambda ~+~\lambda }{2}=-6$

 $6\lambda =-12$

 $\lambda =\frac{-12}{6}$

 $\lambda =-2$

Hence the position vector of Q is,

 $\left( \hat{i}+3\hat{j}+4\hat{k} \right)-2\left( 2\hat{i}-\hat{j}+\hat{k}~ \right)$

$\Rightarrow \hat{i}+3\hat{j}+4\hat{k}-4\hat{i}+2\hat{j}-2\hat{k}$ 

$\Rightarrow -3\hat{i}+5\hat{j}+2\hat{k}$ 

Objective Type Questions

Choose the correct answer from the given four options in each of the Examples 14 to 19.

14. The coordinates of the foot of the perpendicular drawn from the point (2, 5, 7) on the x-axis are given by

a) (2, 0, 0)

b) (0, 5, 0)

c) (0, 0, 7)

d) (0, 5, 7)

Ans: Option (a) is the correct choice.

Depending on the axis on which the perpendicular is dropped, the foot of the perpendicular dropped from point (2, 5, 7) would be (2, 0, 0) 

Because, If the perpendicular is dropped on the x-axis, the y and z axis coordinates will be zero, and the x-axis will be equal to the points in the x-coordinate.

As the x-coordinate of the point is 2, the coordinate of the foot is (2, 0, 0).

15. P is a point on the line segment joining the points (3, 2, –1) and (6, 2, –2). If x-coordinate of P is 5, then its y-coordinate is

a) 2 

b) 1 

c) –1 

d) –2

Ans: Option (a) is the correct choice.

Here let us consider that P divides the line in the ratio :1

So, x-coordinate of line P will be, x=$\frac{\lambda {{x}_{2}}+{{x}_{1}}}{\lambda ~+~1}$

 $5=\frac{6\lambda ~+~3}{\lambda ~+~1}$

 $5\lambda +5=6\lambda +3$

 $6\lambda -5\lambda =5-3$

 $\lambda =2$

Thus the y-coordinate of P is,

 $y=\frac{\lambda {{y}_{2}}+~{{y}_{1}}}{\lambda ~+~1}$

 $y=\frac{2\left( 2 \right)~+~2}{2~+~1}$

 $y=\frac{4~+~2}{3}$

 $y=\frac{6}{3}$

 $y=2$

16. If α, β, γ are the angles that a line makes with the positive direction of x, y, z axis, respectively, then the direction cosines of the line are.

a) $sin~\alpha ,~sin~\beta ,~sin~\gamma $

b) $cos~\alpha ,~cos~\beta ,~cos~\gamma $

c) $tan~\alpha ,~tan~\beta ,~tan~\gamma $

d) $co{{s}^{2}}\alpha ,~co{{s}^{2}}\beta ,~co{{s}^{2}}\gamma $

Ans: Option (b) is the correct choice.

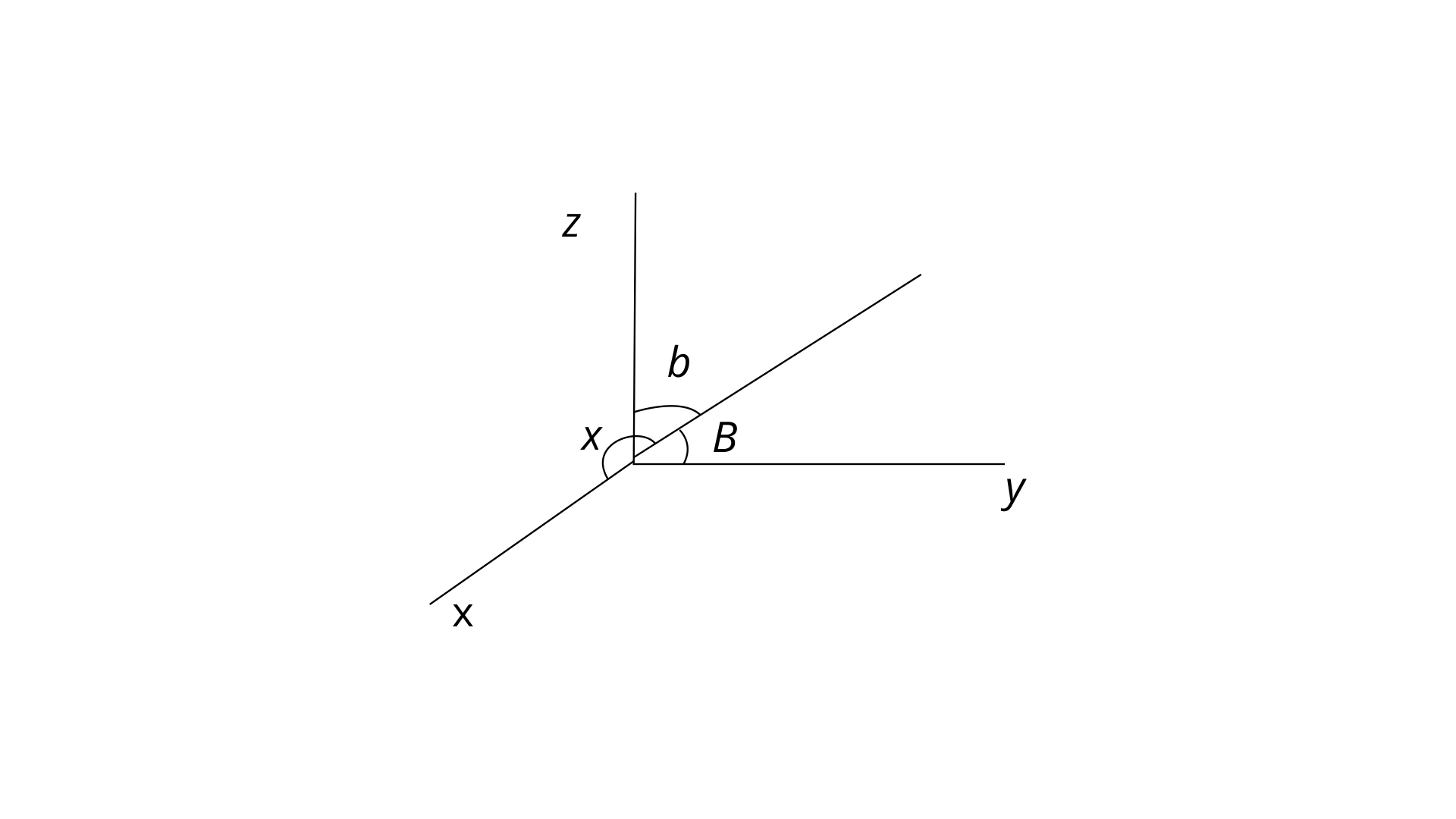
x-axis is making an angle ‘$\alpha $’

y-axis is making an angle ‘$\beta $’

z-axis is making an angle ‘$\gamma $’

Let us consider the direction cosines to be $l,m$ and $n$

Where $l=cos~\alpha $

 $m=cos~\beta $

 $n=cos~\gamma $

Hence the direction cosines are $cos~\alpha ,~cos~\beta ,~cos~\gamma $

17. The distance of a point P (a, b, c) from x-axis is

a) $\sqrt{{{a}^{2}}+{{c}^{2}}}$

b) $\sqrt{{{a}^{2}}+{{b}^{2}}}$

c) $\sqrt{{{b}^{2}}+{{c}^{2}}}$

d) ${{b}^{2}}+{{c}^{2}}$

Ans:  Option (c) is the correct choice. 

Given distance of a point P = (a, b, c)

Let the coordinates of the point on the x-axis be Q (a, 0, 0),

Therefore, distance $=\sqrt{{{(a-a)}^{2}}+{{(b-0)}^{2}}+{{(c-0)}^{2}}}$

Distance $=\sqrt{{{b}^{2}}+{{c}^{2}}}$

18. The equations of x-axis in space are 

a) x = 0, y = 0 

b) x = 0, z = 0 

c) x = 0 

d) y = 0, z = 0

Ans: (D) is the correct answer. 

Spaces have 3 dimensions : x-coordinate axis, y-coordinate axis and z-coordinate axis. Therefore on the x-axis the y- coordinate and z- coordinates are zero.

19. A line makes equal angles with the coordinate axis. Direction cosines of this line are

a) $\pm ~\left( 1,1,1 \right)~$

b) $\pm \left( \frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}} \right)$

c) $\pm \left( \frac{1}{3},\frac{1}{3},\frac{1}{3} \right)$

d) $\pm \left( \frac{1}{\sqrt{3}},\frac{-1}{\sqrt{3}},\frac{-1}{\sqrt{3}} \right)$

Ans: Option (b) is the correct choice.

Allow the line's direction cosines to form an angle $\alpha $ with each of the coordinate axis $l,m$ and $n$

W.K.T ${{l}^{2}}+{{m}^{2}}+{{n}^{2}}=1$

 $co{{s}^{2}}\alpha +co{{s}^{2}}\alpha +co{{s}^{2}}\alpha =1$

 $3co{{s}^{2}}\alpha =1$

 $co{{s}^{2}}\alpha =\frac{1}{3}$

 $cos~\alpha =\sqrt{\frac{1}{3}}$

 $cos~\alpha =\pm \frac{1}{\sqrt{3}}$

As a result, the direction cosines of a line that is equally inclined to the coordinate axis are $\pm \frac{1}{\sqrt{3}}$, $\pm \frac{1}{\sqrt{3}}$ and $\pm \frac{1}{\sqrt{3}}$

That is $\pm \left( \frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}} \right)$

Fill in the blanks in each of the Examples from 20 to 22.

20. If a line makes angles $\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}}$, $\frac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}}$ and $\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}$ with x, y, z axis, respectively, then its direction cosines are _______

Ans: Let $\alpha =\frac{\pi }{2},~\beta =\frac{3\pi }{4}$ and $\gamma =\frac{\pi }{4}$

Therefore the direction cosines of the lines are, 

 $\left( cos~\alpha ,~cos~\beta ,~cos~\gamma  \right)$

W.K.T  $cos~\frac{\pi }{2}=0,~cos~\frac{3\pi }{4}=\frac{-1}{\sqrt{2}}$ and $~cos~\frac{\pi }{4}=\frac{1}{\sqrt{2}}$

$=\pm \left( 0,\frac{-1}{\sqrt{2}},\frac{1}{\sqrt{2}} \right)$ 

21. If a line makes angles α, β, γ with the positive directions of the coordinate axis, then the value of $si{{n}^{2}}\alpha ~+~si{{n}^{2}}\beta ~+~si{{n}^{2}}\gamma $ is _______

Ans: $si{{n}^{2}}\alpha +si{{n}^{2}}\beta +si{{n}^{2}}\gamma =\left( 1~~co{{s}^{2}}\alpha  \right)+\left( 1~~co{{s}^{2}}\beta  \right)+\left( 1~~co{{s}^{2}}\gamma  \right)$

 $si{{n}^{2}}\alpha +si{{n}^{2}}\beta +si{{n}^{2}}\gamma =3~~\left( co{{s}^{2}}\alpha +co{{s}^{2}}\beta +co{{s}^{2}}\gamma  \right)$

 $si{{n}^{2}}\alpha +si{{n}^{2}}\beta +si{{n}^{2}}\gamma =3~~1$

 $si{{n}^{2}}\alpha +si{{n}^{2}}\beta +si{{n}^{2}}\gamma =2$

22. If a line makes an angle of $\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}$ with each of y and z axis, then the angle which it makes with x-axis is _________

Ans: Let the direction cosines form an angle ‘$\alpha $’ on the x-axis, then

 $co{{s}^{2}}\alpha +co{{s}^{2}}\left( \frac{\pi }{4} \right)+co{{s}^{2}}\left( \frac{\pi }{4} \right)=1$

 $co{{s}^{2}}\alpha +\frac{1}{2}+\frac{1}{2}=1$

 $co{{s}^{2}}\alpha =0$

 $cos~\alpha =0$

 $\alpha =co{{s}^{-1}}\left( 0 \right)$

 $\alpha =\frac{\pi }{2}$

23. The points (1, 2, 3), (–2, 3, 4) and (7, 0, 1) are collinear.

Ans:  Let A = (1, 2, 3), B = (–2, 3, 4) and C = (7, 0, 1) respectively.

To find it is collinear calculate distance between the 3 points

For line AB,

$AB=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}+{{({{z}_{2}}-{{z}_{1}})}^{2}}}$

 $AB=\sqrt{{{(-2-1)}^{2}}+{{(3-2)}^{2}}+{{(4-3)}^{2}}}$

 $AB=\sqrt{{{(-3)}^{2}}+{{(1)}^{2}}+{{(1)}^{2}}}$

 $AB=\sqrt{9+1+1}=\sqrt{11}$

For line BC,

$BC=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}+{{({{z}_{2}}-{{z}_{1}})}^{2}}}$

 $BC=\sqrt{{{(7+2)}^{2}}+{{(0-3)}^{2}}+{{(1-4)}^{2}}}$

 $BC=\sqrt{{{(9)}^{2}}+{{(-3)}^{2}}+{{(-3)}^{2}}}$

 $BC=\sqrt{81+9+9}=\sqrt{99}=3\sqrt{11}$

For line AC,

$AC=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}+{{({{z}_{2}}-{{z}_{1}})}^{2}}}$

 $AC=\sqrt{{{(7-1)}^{2}}+\left( 0-2 \right)+{{(1-3)}^{2}}}$

 $AC=\sqrt{{{(6)}^{2}}+{{(-2)}^{2}}+{{(-2)}^{2}}}$

 $AC=\sqrt{36+4+4}=\sqrt{44}=4\sqrt{11}$

So, we can say that AB + BC = $\sqrt{11}+3\sqrt{11}=4\sqrt{11}$ = AC

Hence A, B  and C are all collinear.

24. The vector equation of the line passing through the points (3, 5, 4) and (5, 8, 11) is \[\underline{r}=3\widehat{i}+5\widehat{j}+4\widehat{k}+\lambda \left( 2\widehat{i}+3\widehat{j}+7\widehat{k} \right)\]

Ans: The position vector of the point (3, 5, 4) and (5, 8, 11) is,

$\underset{\scriptscriptstyle-}{a}=3\hat{i}+5\hat{j}+4\hat{k}$ and $\underset{\scriptscriptstyle-}{b}=5\hat{i}+8\hat{j}+11\hat{k}$

The vector equation of a line parallel to the given line that passes through the point is, $\underset{\scriptscriptstyle-}{r}=\underset{\scriptscriptstyle-}{a}+\lambda \left( \underset{\scriptscriptstyle-}{b}-\underset{\scriptscriptstyle-}{a} \right)$

 $\underset{\scriptscriptstyle-}{r}=3\hat{i}+5\hat{j}+4\hat{k}+\lambda \left( \left( 5\hat{i}+8\hat{j}+11\hat{k} \right)-\left( 3\hat{i}+5\hat{j}+4\hat{k} \right) \right)$

 $\underset{\scriptscriptstyle-}{r}=3\hat{i}+5\hat{j}+4\hat{k}+\lambda \left( \left( 5\hat{i}-3\hat{i} \right)+\left( 8\hat{j}-5\hat{j} \right)+\left( 11\hat{k}-4\hat{k} \right) \right)$

Therefore equation of the required line

 $\underset{\scriptscriptstyle-}{r}=3\hat{i}+5\hat{j}+4\hat{k}+\lambda \left( 2\hat{i}+3\hat{j}+7\hat{k} \right)$

Exercise 11.3

Short Answer Questions

1. Find the position vector of a point A in space such that $\underline{OA}$ is inclined at 60º to OX and at 45° to OY and $\left| \underline{OA} \right|$ = 10 units

Ans: Since $\underline{OA}$is inclined to OX at 60º, at 45° to OY and let it make an angle α with OZ.

Therefore, $co{{s}^{2}}45{}^\circ +co{{s}^{2}}60{}^\text{o}+co{{s}^{2}}\alpha =1$

 $\Rightarrow co{{s}^{2}}\alpha =1-\frac{1}{2}-\frac{1}{4}=\frac{1}{4}$

 $\Rightarrow cos\alpha =\frac{1}{2}$

 $\Rightarrow \alpha ={{60}^{\circ }}$

Now, the position vector = $\left| \underline{OA} \right|\left( \frac{1}{2}\hat{i}+\frac{1}{\sqrt{2}}\hat{j}+\frac{1}{2}\hat{k} \right)$

 $~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~=10\left( \frac{1}{2}\hat{i}+\frac{1}{\sqrt{2}}\hat{j}+\frac{1}{2}\hat{k} \right)$

 $~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~=5\hat{i}+5\sqrt{2}\hat{j}+5\hat{k}$

2. Find the vector equation of the line which is parallel to the vector 

$3\hat{i}-2\hat{j}+6\hat{k}$ and which passes through the point (1,-2,3).

Ans: Let $\underset{\scriptscriptstyle-}{a}=3\hat{i}-2\hat{j}+6\hat{k}~$and  $\underset{\scriptscriptstyle-}{a}=\hat{i}-2\hat{j}+3\hat{k}~$

The vector which is parallel to vector $3\hat{i}-2\hat{j}+6\hat{k}$and passing through $\hat{i}-2\hat{j}+3\hat{k}$ is $\underline{r.}$

Therefore, $\underset{\scriptscriptstyle-}{r}=\hat{i}-2\hat{j}+3\hat{k}~+\lambda (3\hat{i}-2\hat{j}+6\hat{k}$).

3. Show tha the lines $\frac{\text{x-1}}{\text{2}}\text{=}\frac{\text{y-2}}{\text{3}}\text{=}\frac{\text{z-3}}{\text{4}}$and $\frac{\text{x-4}}{\text{5}}\text{=}\frac{\text{y-1}}{\text{2}}\text{=z}$ intersect. Also find their point of intersections.

Ans: We have, ${{x}_{1}}=1,~{{y}_{1}}=3,~{{z}_{1}}=4$and ${{a}_{1}}=2,~{{b}_{1}}=3,~{{c}_{1}}=4$

Also, ${{x}_{2}}=4,~{{y}_{2}}=1,~{{z}_{2}}=0$and ${{a}_{2}}=5,~{{b}_{2}}=2,~{{c}_{2}}=1$

If two lines intersect, then the shortest distance will be zero.

Shortest distance b/w two given lines, 

$=\frac{\left| \begin{matrix}{{x}_{2}}-{{x}_{1}} & {{y}_{2}}-{{y}_{1}} & {{z}_{2}}-{{z}_{1}}  \\{{a}_{1}} & {{b}_{1}} & {{c}_{1}}  \\{{a}_{2}} & {{b}_{2}} & {{c}_{2}}  \\\end{matrix} \right|}{\sqrt{{{\left( {{b}_{1}}{{c}_{2}}-{{b}_{2}}{{c}_{1}} \right)}^{2}}+{{\left( {{c}_{1}}{{a}_{2}}-{{c}_{2}}{{a}_{1}} \right)}^{2}}+{{\left( {{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}} \right)}^{2}}}}$

$=\frac{\left| \begin{matrix}4-1 & 1-3 & 0-4  \\2 & 3 & 4  \\5 & 2 & 1  \\\end{matrix} \right|}{\sqrt{{{\left( 3\times 1-2\times 4 \right)}^{2}}+{{\left( 1\times 5-1\times 2 \right)}^{2}}+{{\left( 2\times 2-5\times 3 \right)}^{2}}}}=\frac{3\left( 2-8 \right)+1\left( 2-20 \right)-3\left( 4-15 \right)}{\sqrt{470}}=0$

Therefore the given lines intersect.

Now, for finding the point of intersection,

 $\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}=\lambda $

 $\Rightarrow x=2\lambda +1,~y=3\lambda +2,~z=4\lambda +3$

Now substituting these values in the equation of the second line.

 $\frac{2\lambda +1-4}{5}=\frac{3\lambda +2-1}{2}=4\lambda +3$

 $\Rightarrow 2\lambda -3=20\lambda +15$

 $\Rightarrow 18\lambda =-18$

 $\Rightarrow \lambda =-1$

So the required point is, 

 $x=2\times -1+1=-1,~y=3\times -1+2=-1,~z=4\times -1+3=-1$

Thus the line intersects at (-1,-1,-1).

4. Find the angle between the lines $\underset{\scriptscriptstyle-}{r}=3\hat{i}-2\hat{j}+6\hat{k}+\lambda \left( 2\hat{i}+\hat{j}+2\hat{k} \right)$ and $\underset{\scriptscriptstyle-}{r}=2\hat{j}-5\hat{k}+\mu \left( 6\hat{i}+3\hat{j}+2\hat{k} \right)$.

Ans:  We have  $\underset{\scriptscriptstyle-}{r}=3\hat{i}-2\hat{j}+6\hat{k}+\lambda \left( 2\hat{i}+\hat{j}+2\hat{k} \right)$and $\underset{\scriptscriptstyle-}{r}=2\hat{j}-5\hat{k}+\mu \left( 6\hat{i}+3\hat{j}+2\hat{k} \right)$.

Where, ${{a}_{1}}=3\hat{i}-2\hat{j}+6\hat{k}~,~{{b}_{1}}=2\hat{i}+\hat{j}+2\hat{k}$and ${{a}_{2}}=2\hat{j}-5\hat{k}$,${{b}_{2}}=6\hat{i}+3\hat{j}+2\hat{k}$

Angle between lines, $Cos\theta =\frac{\left| {{b}_{1}}.{{b}_{2}} \right|}{\left| {{b}_{1}}\left| . \right|{{b}_{2}} \right|}=\frac{12+3+4}{\sqrt{4+1+4}.\sqrt{36+9+4}}=\frac{19}{3\times 7}=\frac{19}{21}$

Hence, $\theta =co{{s}^{-1}}\left( \frac{19}{21} \right)$

5. Prove that the line through A(0,-1,-1) and B(4,5,1) intersects the line through C(3,9,4) and D(-4,4,4).

Ans: The cartesian equation of a line passing through two points $\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)~and~\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)$ is $\frac{x-{{x}_{1}}}{{{x}_{2}}-{{x}_{1}}}=\frac{y-{{y}_{1}}}{{{y}_{2}}-{{y}_{1}}}=\frac{z-{{z}_{1}}}{{{z}_{2}}-{{z}_{1}}}$

Equation of  line passing through points A(0,-1,-1) and B(4,5,1) is: 

 $\frac{x-0}{4}=\frac{y+1}{6}=\frac{z+1}{2}$

 $\Rightarrow \frac{x}{4}=\frac{y+1}{6}=\frac{z+1}{2}$

Similarly, Equation of  line passing through points C(3,9,4) and D(-4,4,4) is :

 $\frac{x-3}{-7}=\frac{y-9}{-5}=\frac{z-4}{0}$

 $\Rightarrow \frac{x-3}{-7}=\frac{y-9}{-5}=\frac{z-4}{0}$

If the lines intersect then the shortest distance b/w them is zero.

Shortest distance b/w two given lines, $=\frac{\left| \begin{matrix}

   $=\frac{\left| \begin{matrix}{{x}_{2}}-{{x}_{1}} & {{y}_{2}}-{{y}_{1}} & {{z}_{2}}-{{z}_{1}}  \\{{a}_{1}} & {{b}_{1}} & {{c}_{1}}  \\{{a}_{2}} & {{b}_{2}} & {{c}_{2}}  \\\end{matrix} \right|}{\sqrt{{{\left( {{b}_{1}}{{c}_{2}}-{{b}_{2}}{{c}_{1}} \right)}^{2}}+{{\left( {{c}_{1}}{{a}_{2}}-{{c}_{2}}{{a}_{1}} \right)}^{2}}+{{({{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}})}^{2}}^{{}}}}$

 $=\frac{\left| \begin{matrix}3-0 & 9+1 & 4+!  \\4 & 6 & 2  \\-7 & -5 & 0  \\\end{matrix} \right|}{\sqrt{{{\left( 6\times 0+6\times 5 \right)}^{2}}+{{\left( 2\times -7-0\times 4 \right)}^{2}}+{{\left( 4\times -5+7\times 6 \right)}^{2}}}}=\frac{30-140+110}{\sqrt{780}}=0$

So the given lines intersect.

6. Prove that the lines $x=py+q,~z=ry+s~and~x=p'y+q',~z=r'y+s'$are perpendicular if $pp'+rr'+1=0$

Ans: We have, $x=py+q\Rightarrow y=\frac{x-q}{p}$-----(i)

$z=ry+s\Rightarrow y=\frac{z-s}{r}$----------(ii)

From eq. (i) and (ii)

$\frac{x-q}{p}=y=\frac{z-s}{r}$ -----------(iii)

Similarly, $\frac{x-q'}{p'}=y=\frac{z-s'}{r'}$-----(iv)

From eq. (iii) and (iv)

We have, ${{a}_{1}}=p,~{{b}_{1}}=1,~{{c}_{1}}=r$and ${{a}_{2}}=p',~{{b}_{2}}=1,~{{c}_{2}}=r'$

If two lines are perpendicular then, ${{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}+{{c}_{1}}{{c}_{2}}=0$

Now substituting these values 

$pp'+1+rr'=0$ (Hence proved)

7. Find the equation of a plane which bisects perpendicularly the line joining the points A(2,3,4) and B(4,5,8) at right angles.

Ans: We have points A(2,3,4) and B(4,5,8).

The vector form of line joining these points = $\underset{\scriptscriptstyle-}{N}=\left( 4-2 \right)\hat{i}+\left( 5-3 \right)\hat{j}+\left( 8-4 \right)\hat{k}=2\hat{i}+2\hat{j}+4\hat{k}$

Midpoint of AB is =$\left( \frac{4+2}{2},\frac{3+5}{3},\frac{4+8}{2} \right)=\left( 3,4,6 \right)$

No the equation of required plane is $\left( \underset{\scriptscriptstyle-}{r}-a \right).\underset{\scriptscriptstyle-}{N}=0$ 

Let $\underset{\scriptscriptstyle-}{r}=x\hat{i}+y\hat{j}+z\hat{k}$

 $\Rightarrow \left[ \left( x-3 \right)\hat{i}+\left( y-4 \right)\hat{j}+\left( z-6 \right)\hat{k} \right].\left( 2\hat{i}+2\hat{j}+4\hat{k} \right)=0$

 $\Rightarrow 2x-6+2y-8+4z-24=0$

 $\Rightarrow 2x+2y+4z=38$

 $\Rightarrow x+y+z=19$

Thus the equation of plane is $x+y+z=19$.

8. Find the equation of plane which is at distance $\text{3}\sqrt{\text{3}}$ units from origin and the normal to which is equally inclined to coordinate axes.

Ans: Since normal is equally inclined to coordinate axes.

Therefore, $3co{{s}^{2}}\alpha =1\Rightarrow cos\alpha =\frac{1}{\sqrt{3}}$

So the normal is $\underset{\scriptscriptstyle-}{N}=\left( \frac{1}{\sqrt{3}}\hat{i}+\frac{1}{\sqrt{3}}\hat{j}+\frac{1}{\sqrt{3}}\hat{k} \right)$

The equation of plane is $\underset{\scriptscriptstyle-}{r}.\hat{N}=3\sqrt{3}$ 

[Since, Vector equation of a plane from origin $\underset{\scriptscriptstyle-}{r}.\hat{N}=p$]

 $\left( x\hat{i}+y\hat{j}+z\hat{k} \right).\frac{\left( \frac{1}{\sqrt{3}}\hat{i}+\frac{1}{\sqrt{3}}\hat{j}+\frac{1}{\sqrt{3}}\hat{k} \right)}{1}=3\sqrt{3}$

 $\Rightarrow \frac{x}{\sqrt{3}}+\frac{y}{\sqrt{3}}+\frac{z}{\sqrt{3}}=3\sqrt{3}$

 $\Rightarrow x+y+z=3.3=9$

So the required equation of plane is $x+y+z=9$.

9. If the line drawn from the point (-2,-1,-3) meets a plane at right angle at the point (1,-3,3), find the equation of the plane.

Ans: Since the line drawn from the point (-2,-1,-3) meets the plane at right angle at the point (1,-3,3). Hence the normal of the plane is $\underset{\scriptscriptstyle-}{N}=\left( -2-1 \right)\hat{i}+\left( -1+3 \right)\hat{j}+\left( -3-3 \right)\hat{k}=-3\hat{i}+2\hat{j}-6\hat{k}$

Since the point (1,-3,3) is on the plane that means the plane is passing through this point.

Now, the equation of a plane passing through the point a and having normal $\underset{\scriptscriptstyle-}{N}$is $\left( \underset{\scriptscriptstyle-}{r}-a \right).\underset{\scriptscriptstyle-}{N}=0$

 $\Rightarrow \left[ \left( x-1 \right)\hat{i}+\left( y+3 \right)\hat{j}+\left( z-3 \right)\hat{k} \right].\left( -3\hat{i}+2\hat{j}-6\hat{k} \right)=0$

 $\Rightarrow -3\left( x-1 \right)+2\left( y+3 \right)-6\left( z-3 \right)=0$

 $\Rightarrow -3x+3+2y+6-6z+18=0$

 $\Rightarrow -3x+2y-6z+27=0$

 $\Rightarrow 3x-2y+6z-27=0$

10. Find the equation of the plane through the points (2,1,0), (3,-2,-2) and (3,1,7).

Ans: We know that if a plane is passing through three points $\left( {{x}_{1}},~{{y}_{1}},~{{z}_{1}} \right),~\left( {{x}_{2}},~{{y}_{2}},~{{z}_{2}} \right)$and $\left( {{x}_{3}},~{{y}_{3}},~{{z}_{3}} \right)$ Then the equation of plane is :

           $\left| \begin{matrix}x-{{x}_{1}} & y-{{y}_{1}} & z-{{z}_{1}}  \\{{x}_{2}}-{{x}_{1}} & {{y}_{2}}-{{y}_{1}} & {{z}_{2}}-{{z}_{1}}  \\{{x}_{3}}-{{x}_{1}} & {{y}_{3}}-{{y}_{1}} & {{z}_{3}}-{{z}_{1}}  \\\end{matrix} \right|=0$

$\left| \begin{matrix}x-2 & y-{{y}_{1}} & z-0  \\3-2 & -2-1 & -2-0  \\3-2 & 1-1 & 7-0  \\\end{matrix} \right|=0$

$\left| \begin{matrix}x-2 & y-1 & z-0  \\1 & -3 & -2  \\1 & 0 & 7  \\\end{matrix} \right|=0$

$\Rightarrow \left( x-2 \right)\left( -21 \right)-\left( y-1 \right)\left( 7+2 \right)+z\left( 0+3 \right)=0$

$\Rightarrow -21x+42-9y+9+3z=0$

$\Rightarrow -21x-9y+3z+51=0$

$\Rightarrow 7x+3y-z-17=0$

$\Rightarrow 7x+3y-z=17$

So the required equation of plane $7x+3y-z=17$.

11. Find the equations of two lines through the origin which intersect the line $\frac{x-3}{2}=\frac{y-3}{1}=\frac{z}{1}$at angles of $\frac{\pi }{3}$ each.

Ans: Given equation of line is $\frac{x-3}{2}=\frac{y-3}{1}=\frac{z}{1}=\lambda $-------------(i)

So, the DR’s of the given line is 2,1,1 and Dc’s $\frac{2}{\sqrt{6}},\frac{2}{\sqrt{6}},\frac{2}{\sqrt{6}}$

Also the required line makes an angle $\frac{\pi }{3}$ with the given line 

From eq.(i) $x=2\lambda +3,~y=\lambda +3,~z=\lambda $

The angles b/w two lines,

 $cos\theta =\frac{{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}+{{c}_{1}}{{c}_{2}}}{\sqrt{{{a}_{1}}^{2}+{{b}_{1}}^{2}+{{c}_{1}}^{2}}\sqrt{{{a}_{2}}^{2}+{{b}_{2}}^{2}+{{c}_{2}}^{2}}}$

 $\Rightarrow cos\frac{\pi }{3}=\frac{2\left( 2\lambda +3 \right)+1\left( \lambda +3 \right)+\lambda }{\sqrt{4+1+1}\sqrt{{{\left( 2\lambda +3 \right)}^{2}}+{{\left( \lambda +3 \right)}^{2}}+{{\lambda }^{2}}}}$

 $\Rightarrow \frac{\sqrt{6}}{2}=\frac{6\lambda +9}{\sqrt{6{{\lambda }^{2}}+18\lambda +18}}$

Squaring on both sides

 $6\left( {{\lambda }^{2}}+3\lambda +3 \right)=4\lambda +6$

 $\Rightarrow 6{{\lambda }^{2}}+18\lambda +18=4\lambda +6$

 $\Rightarrow 6{{\lambda }^{2}}+14\lambda +12=0$

 $\Rightarrow 3{{\lambda }^{2}}+7\lambda +6=0$

 $\Rightarrow 3{{\lambda }^{2}}+3\lambda +6\lambda +6=0$

 $\Rightarrow 3\lambda \left( \lambda +1 \right)+6\left( \lambda +1 \right)=0$

 $\Rightarrow \lambda =~-1,~-2$

So the Direction ratios of the lines are $x=2\lambda +3,~y=\lambda +3,~z=\lambda $

 $\Rightarrow \left( 1,2,-1 \right)~and~\left( -1,~1,~-2 \right)$

Hence the equation of lines passing through origin and having above DR’s.

 $\frac{x}{1}=\frac{y}{2}=\frac{z}{-1}~and~\frac{x}{-1}=\frac{y}{1}=\frac{z}{-2}~$

12. Find the angle between the lines whose direction cosines are given by the equations $l+m+n=0,~{{l}^{2}}+{{m}^{2}}-{{n}^{2}}=0$.

Ans: Elimination n from both equations.

 $l+m+n=0\Rightarrow n=~-l-m$

 ${{l}^{2}}+{{m}^{2}}-{{n}^{2}}=0$

 $\Rightarrow {{l}^{2}}+{{m}^{2}}-{{\left( l+m \right)}^{2}}=0$

 $\Rightarrow {{l}^{2}}+{{m}^{2}}-{{l}^{2}}-{{m}^{2}}-2ml=0$

 $\Rightarrow ml=0$

Since, $n+l+m=0$

Hence, $\Rightarrow m\left( -m-n \right)=0$

 $\Rightarrow m\left( m+n \right)=0$

 $\Rightarrow m=0~~and~m=~-n$

From $m=0$we get $n=-l$

And by $m=~-n$ we get $l=0$

So the DR’s of lines are proportional to $0,-n,n~and~-n,0,n$i.e. $0,-1,1~and~-1,0,1$

Now the angle b/w two lines $Cos\theta =\frac{a.b}{\left| a \right|\left| b \right|}=\frac{1}{\sqrt{2}.\sqrt{2}}=\frac{1}{2}$

Thus, $\theta ={{60}^{\circ }}$

13. If a variable line in two adjacent positions has direction cosines $l,m,n$,$l+\delta l,~m+\delta m,~n+\delta n$show that the small angle $\delta \theta $between the two positions is given by $\delta {{\theta }^{2}}=\delta {{l}^{2}}+\delta {{m}^{2}}+\delta {{n}^{2}}$

Ans: Since we know that, ${{l}^{2}}+{{m}^{2}}+{{n}^{2}}=0$

 ${{\left( l+\delta l \right)}^{2}}+{{\left( m+\delta m \right)}^{2}}+{{\left( ~n+\delta n \right)}^{2}}=1$

 $\Rightarrow {{l}^{2}}+\delta {{l}^{2}}+2l.\delta l+{{m}^{2}}+2m.\delta m+{{\left( \delta m \right)}^{2}}+{{n}^{2}}+2n.\delta n+{{\left( \delta n \right)}^{2}}=1$

$\Rightarrow {{(\delta l)}^{2}}+{{\left( \delta m \right)}^{2}}+{{\left( \delta n \right)}^{2}}=-2\left( l.\delta l+m.\delta m+n.\delta n \right)$ 

$\Rightarrow \left( l.\delta l+m.\delta m+n.\delta n \right)=\frac{-1}{2}[\left( \delta l{{)}^{2}}+{{\left( \delta m \right)}^{2}}+{{\left( \delta n \right)}^{2}} \right]$---------(i)

Let $\underset{\scriptscriptstyle-}{a}~and~\underset{\scriptscriptstyle-}{b}$are unit vectors along a line having DR’s $l,m,n$and $l+\delta l,~m+\delta m,~n+\delta n$.

Given, the angle b/w these lines is $\delta \theta .$

 $Cos\theta =\frac{\underset{\scriptscriptstyle-}{a}.\underset{\scriptscriptstyle-}{b}}{\left| a \right|.\left| b \right|}=l\left( l+\delta l \right)+m\left( ~m+\delta m \right)+n\left( ~n+\delta n \right)$

 $\Rightarrow Cos\theta =\left( {{l}^{2}}+{{m}^{2}}+{{n}^{2}} \right)+\left( l.\delta l+m.\delta m+n.\delta n \right)$

$\Rightarrow Cos\theta =1-\frac{1}{2}[\left( \delta l{{)}^{2}}+{{\left( \delta m \right)}^{2}}+{{\left( \delta n \right)}^{2}} \right]$  [Substituting the value from eq. (i)]

 $\Rightarrow 2\left( 1-Cos\theta  \right)=[\left( \delta l{{)}^{2}}+{{\left( \delta m \right)}^{2}}+{{\left( \delta n \right)}^{2}} \right]$

$\Rightarrow 4si{{n}^{2}}\frac{\theta }{2}={{(\delta l)}^{2}}+{{\left( \delta m \right)}^{2}}+{{\left( \delta n \right)}^{2}}$  [Since $si{{n}^{2}}\frac{\theta }{2}\approx \frac{\theta }{2}\Rightarrow si{{n}^{2}}\frac{\theta }{2}\approx {{\left( \frac{\theta }{2} \right)}^{2}}$]

 $\Rightarrow {{\theta }^{2}}={{(\delta l)}^{2}}+{{\left( \delta m \right)}^{2}}+{{\left( \delta n \right)}^{2}}$

14. O is the origin and A is (a,b,c). Find the direction cosines of the line OA and the equation of plane through A at right angle to OA.

Ans: The point O and A (a,b,c) is given.

Hence, $\underline{OA}=a\hat{i}+b\hat{j}+c\hat{k}$

The DC’s of line  $\underline{OA}$is $\frac{a}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}},\frac{b}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}},\frac{c}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}$

Since, the plane is passing through the point A and at the right angle to OA. Hence the vector $\underline{OA}$will be the normal vector to the plane.

Therefore, $\underline{OA}=\underset{\scriptscriptstyle-}{n}=a\hat{i}+b\hat{j}+c\hat{k}$

Now the equation of required plane, 

 $\left( \underset{\scriptscriptstyle-}{r}-a \right).\underset{\scriptscriptstyle-}{n}=0$

 $\Rightarrow \left[ \left( x-a \right)\hat{i}+\left( y-b \right)\hat{j}+\left( z-c \right)\hat{k} \right].\left( a\hat{i}+b\hat{j}+c\hat{k} \right)=0$

 $\Rightarrow ax+by+cz={{a}^{2}}+{{b}^{2}}+{{c}^{2}}$

15. Two systems of rectangular axis have the same origin. If a plane cuts them at distances a,b,c and a’, b’, c’ respectively, from the origin, prove that 

$\frac{1}{{{a}^{2}}}+\frac{1}{{{b}^{2}}}+\frac{1}{{{c}^{2}}}=\frac{1}{a{{'}^{2}}}+\frac{1}{b{{'}^{2}}}+\frac{1}{c{{'}^{2}}}$.

Ans: Let $OX,~OY,~OZ$and $ox,~oy,~oz$are two rectangular systems.

A plane cuts these two systems at distances a,b,c and a’, b’, c’ respectively.

So the equations of planes.

$\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$-----------(i)

And, $\frac{x}{a'}+\frac{y}{b'}+\frac{z}{c'}=1$---------(ii)

Since, the systems have the same origin and the plane cuts both the systems.

So the perpendicular distances from the origin to the plane must be the same.

$\frac{0+0+0-1}{\sqrt{\frac{1}{{{a}^{2}}}+\frac{1}{{{b}^{2}}}+\frac{1}{{{c}^{2}}}}}=\frac{0+0+0-1}{\sqrt{\frac{1}{a{{'}^{2}}}+\frac{1}{b{{'}^{2}}}+\frac{1}{c{{'}^{2}}}}}$

 $\Rightarrow \frac{1}{{{a}^{2}}}+\frac{1}{{{b}^{2}}}+\frac{1}{{{c}^{2}}}=\frac{1}{a{{'}^{2}}}+\frac{1}{b{{'}^{2}}}+\frac{1}{c{{'}^{2}}}$

Long Answer Questions

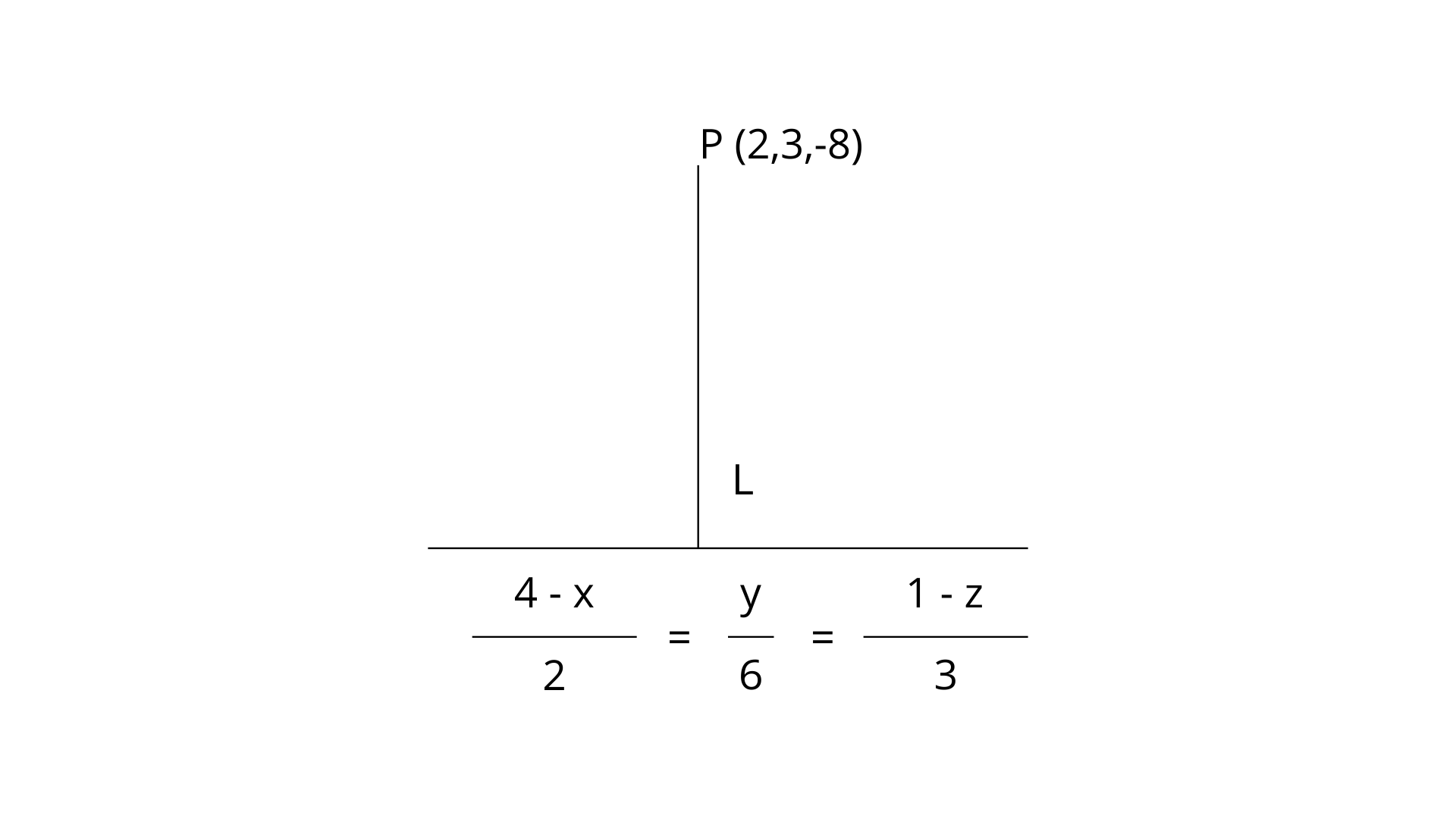
16.  Find the foot of perpendicular from the point (2, 3, –8) to the line $\frac{\text{4 }\!\!~\!\!\text{ - }\!\!~\!\!\text{ x}}{\text{2}}\text{=}\frac{\text{y}}{\text{6}}\text{=}\frac{\text{1 }\!\!~\!\!\text{ - }\!\!~\!\!\text{ z}}{\text{3}}\text{.}$ Also, find the perpendicular distance from the given point to the line.

Ans: We have equation of line $\frac{4~-~x}{2}=\frac{y}{6}=\frac{1~-~z}{3}$

 $\Rightarrow \frac{x~-~4}{-2}=\frac{y}{6}=\frac{z~-~1}{-3}=\lambda $

$\Rightarrow x=-2\lambda +4,~y=6\lambda $ and $z=-3\lambda +1$

Let the coordinates of L be ($4-2\lambda ,~6\lambda ,~1-3\lambda $) and direction ratios of PL are proportional to ($4-2\lambda -2,~6\lambda -3,~1-3\lambda +8$) i.e.,$(2-2\lambda ,~6\lambda -3,~9-3\lambda $)

Also, direction ratios are proportional to -2, 6, -3. Since, PL is perpendicular to the given line.

 $\therefore -2\left( 2-2\lambda  \right)+6\left( 6\lambda -3 \right)-3\left( 9-3\lambda  \right)=0$

 $\Rightarrow -4+4\lambda +36\lambda -18-27+9\lambda =0$

 $\Rightarrow 49\lambda =49\Rightarrow \lambda =1$

So, the coordinates of L are ($4-2\lambda ,~6\lambda ,~1-3\lambda )$ i.e, (2, 6, -2).

\[\frac{4-x}{2}=\frac{y}{6}=\frac{1-z}{3}\]

Also, length of PL $=\sqrt{{{(2-2)}^{2}}+{{(6-3)}^{2}}+{{(-2+8)}^{2}}}$

$=\sqrt{0+9+36}=3\sqrt{5}~units$

17. Find the distance of a point (2, 4, -1) from the line $\frac{\text{x+5}}{\text{1}}\text{=}\frac{\text{y+3}}{\text{4}}\text{=}\frac{\text{z-6}}{\text{-9}}$.

Ans: We have equation of the line as $\frac{x+5}{1}=\frac{y+3}{4}=\frac{z-6}{-9}=\lambda $

 $\Rightarrow x=\lambda -5,~y=4\lambda -3,~z=6-9\lambda $

Let the coordinate of L be $\left( \lambda -5,4\lambda -3,6-9\lambda  \right)$, then Dr’s of PL are $\left( \lambda -7,~4\lambda -7,~7-9\lambda  \right)$

Also, the direction ratios of a given line are proportional to 1, 4, -9.

Since, PL is perpendicular to the given line.

∴$\left( \lambda -7 \right).1+\left( 4\lambda -7 \right).4+\left( 7-9\lambda  \right).\left( -9 \right)=0$

 $\Rightarrow \lambda -7+16\lambda -28-63+81\lambda =0$

 $\Rightarrow 98\lambda =98\Rightarrow \lambda =1$

So the coordinates of L are (-4, 1, -3)

∴ Required distance, PL $=\sqrt{{{(-4-2)}^{2}}+{{(1-4)}^{2}}+{{(-3+1)}^{2}}}$

$=\sqrt{36+9+4}=7~units$

18. Find the length and the foot of perpendicular from the point $\left( \text{1,}\frac{\text{3}}{\text{2}}\text{,2} \right)\text{ }\!\!~\!\!\text{ }$to the plane 2x – 2y + 4z + 5 = 0.

Ans: The equation of the plane is 2x – 2y + 4z + 5 = 0  ------(i)

 $\Rightarrow \vec{n}=2\hat{i}-2\hat{j}+4\hat{k}$

So, the equation of line through $\left( 1,\frac{3}{2},2 \right)$ and parallel to $\vec{n}$ is given by

 $\frac{x-1}{2}=\frac{y~-~\frac{3}{2}}{-2}=\frac{z~-2}{4}=\lambda $

 $\Rightarrow x=2\lambda +1,~y=-2\lambda +\frac{3}{2}~and~z=4\lambda +2$

If this point lies on the given plane, then

$2\left( 2\lambda +1 \right)-2\left( -2\lambda +\frac{3}{2} \right)+4\left( 4\lambda +2 \right)+5=0$   [Using Eq. (i)]

 $\Rightarrow 4\lambda +2+4\lambda -3+16\lambda +8+5=0$

 $\Rightarrow 24\lambda =-12\Rightarrow \lambda =\frac{-1}{2}$

∴ Required foot of perpendicular

$=\left[ 2\left( \frac{-1}{2} \right)+1,-2\left( \frac{-1}{2} \right)+\frac{3}{2},4\left( \frac{-1}{2} \right)+2 \right]$ i.e., $\left( 0,\frac{5}{2},0 \right)$

∴ Required length of perpendicular $=\sqrt{{{(1-0)}^{2}}+{{\left( \frac{3}{2}-\frac{5}{2} \right)}^{2}}+{{\left( 2-0 \right)}^{2}}}$

 $=\sqrt{1+1+4}=\sqrt{6}~units$

19. Find the equations of the line passing through the point (3,0,1) and parallel to the planes x + 2y = 0 and 3y – z = 0.

Ans: The equations of the two planes are x + 2y = 0 and 3y – z = 0.

Let $\overrightarrow{{{n}_{1}}}$  and $\overrightarrow{{{n}_{2}}}$ are the normal of two planes, respectively.

∴ $\overrightarrow{{{n}_{1}}}=\hat{i}+2\hat{j}$ and $\overrightarrow{{{n}_{2}}}=3\hat{i}-\hat{k}$

Since, the required line is parallel to the given two planes.

Therefore, $\vec{b}=\overrightarrow{{{n}_{1}}}\times \overrightarrow{{{n}_{2}}}=\left| _{_{0~~~~~~~~~~3~~~~~~~~~-1}^{1~~~~~~~~~~2~~~~~~~~~~~~0}}^{~~~\hat{i}~~~~~~\hat{j}~~~~~~~~\hat{k}~~~} \right|$

 $=\hat{i}\left( -2 \right)-\hat{j}\left( -1 \right)+\hat{k}\left( 3 \right)$

 $=-2\hat{i}+\hat{j}+3\hat{k}$

So, the equation of the lines through the point (3, 0, 1) and parallel to the given two planes are:

 $\left( x-3 \right)\hat{i}+\left( y-0 \right)\hat{j}+\left( z-1 \right)\hat{k}+\lambda \left( -2\hat{i}+\hat{j}+3\hat{k} \right)$

 $\Rightarrow \left( x-3 \right)\hat{i}+y\hat{j}+\left( z-1 \right)\hat{k}+\lambda \left( -2\hat{i}+\hat{j}+3\hat{k} \right)$

 $\left( x-3 \right)\hat{i}+\left( y-0 \right)\hat{j}+\left( z-1 \right)\hat{k}=\lambda \left( -2\hat{i}+\hat{j}+3\hat{k} \right)$

 $\Rightarrow \left( x-3 \right)\hat{i}+y\hat{j}+\left( z-1 \right)\hat{k}=\lambda \left( -2\hat{i}+\hat{j}+3\hat{k} \right)$

20. Find the equation of the plane through the points (2, 1, –1) and (–1, 3, 4), and perpendicular to the plane x – 2y + 4z = 10.

Ans: The equation of the plane through the points (2, 1, –1) is

 $a\left( x-2 \right)+b\left( y-1 \right)+c\left( z+1 \right)=0~----\left( i \right)$

Since this passing through (–1, 3, 4).

∴ $a\left( -1-2 \right)+b\left( 3-1 \right)+c\left( 4+1 \right)=0$

 $\Rightarrow -3a+2b+5c=0----\left( ii \right)$

Since the plane (i) is perpendicular to the given plane x – 2y + 4z = 10.

∴ $1.a-2.b+4.c=0$

 $\Rightarrow a-2b+4c=0----\left( iii \right)$

On solving Eqs. (ii) and (iii), we get

 $\frac{a}{8+10}=\frac{-b}{-17}=\frac{c}{4}=\lambda $

 $\Rightarrow a=18\lambda ,~b=17\lambda ,~c=4\lambda $

From Eq.(i),

 $18\lambda \left( x-2 \right)+17\lambda \left( y-1 \right)+4\lambda \left( z+1 \right)=0$

 $\Rightarrow 18x-36+17y-17+4z+4=0$

 $\Rightarrow 18x+17y+4z-49=0$

∴ $18x+17y+4z=49$

21.  Find the shortest distance between the lines given by \[\overrightarrow{r}=\left( 8+3\lambda  \right)\widehat{i}-\left( 9+16\lambda  \right)\widehat{j}+\left( 10+7 \right)\widehat{k}\] and  \[\overrightarrow{r}=15\widehat{i}+29\widehat{j}+5\widehat{k}+\mu \left( 3\widehat{i}+8\widehat{j}-5\widehat{k} \right)\].

Ans: We have, $\overrightarrow{{{r}_{{}}}}=\left( 8+3\lambda  \right)\hat{i}-\left( 9+16\lambda  \right)\hat{j}+\left( 10+7\lambda  \right)\hat{k}$

 $=8\hat{i}-9\hat{j}+10\hat{k}+\lambda \left( 3\hat{i}-16\hat{j}+7\hat{k}~ \right)$

$\overrightarrow{{{a}_{1}}}=8\hat{i}-9\hat{j}+10\hat{k}$ and $\overrightarrow{{{b}_{1}}}=\left( 3\hat{i}-16\hat{j}+7\hat{k}~ \right)---\left( i \right)$ 

Also, $\overrightarrow{{{r}_{{}}}}=15\hat{i}+29\hat{j}+5\hat{k}+\mu \left( 3\hat{i}+8\hat{j}-5\hat{k} \right)$.

$\Rightarrow \overrightarrow{{{a}_{2}}}=15\hat{i}+29\hat{j}+5\hat{k}$ and $\overrightarrow{{{b}_{2}}}=\left( 3\hat{i}+8\hat{j}-5\hat{k}~ \right)---\left( ii \right)$

Now, shortest distance between two lines is given by $\left| \frac{\left( \overrightarrow{{{b}_{1}}}~\times \overrightarrow{~{{b}_{2}}} \right).\left( \overrightarrow{{{a}_{1}}}~-\overrightarrow{~{{a}_{2}}} \right)}{\left| \overrightarrow{{{b}_{1}}}~\times \overrightarrow{~{{b}_{2}}} \right|} \right|$

∴ $\overrightarrow{{{b}_{1}}}~\times \overrightarrow{~{{b}_{2}}}=\left| _{_{3~~~~~~~~~~8~~~~~~~~~~-5}^{3~~~~~~~-16~~~~~~~~~~7}}^{~~~\hat{i}~~~~~~\hat{j}~~~~~~~~\hat{k}~~~} \right|$

 $=\left( 80-56 \right)\hat{i}-\left( -15-21 \right)\hat{j}+\left( 24+48 \right)\hat{k}$

 $=24\hat{i}+36\hat{j}+72\hat{k}$

 $\left| \overrightarrow{{{b}_{1}}}~\times \overrightarrow{~{{b}_{2}}} \right|=\sqrt{{{24}^{2}}+{{36}^{2}}+{{72}^{2}}}$

 $=12\sqrt{{{2}^{2}}+{{3}^{2}}+{{6}^{2}}}=84$

And $\left( \overrightarrow{{{a}_{1}}}~-\overrightarrow{~{{a}_{2}}} \right)=\left( 15-8 \right)\hat{i}+\left( 29+9 \right)\hat{j}+\left( 5-10 \right)\hat{k}$

 $=7\hat{i}+38\hat{j}-5\hat{k}$

shortest distance $=\left| \frac{\left( 24\hat{i}+36\hat{j}+72\hat{k} \right).\left( 7\hat{i}+38\hat{j}-5\hat{k} \right)}{84} \right|$

$=\left| \frac{168+1368-360}{84} \right|=\left| \frac{1176}{84} \right|=14~units$

22.  Find the equation of the plane which is perpendicular to the plane 5x + 3y + 6z + 8 = 0 and which contains the line of intersection of the planes x + 2y + 3z – 4 = 0 and 2x + y – z + 5 = 0.

Ans: The equation of a plane through the line of intersection of the planes

x + 2y + 3z – 4 = 0 and 2x + y – z + 5 = 0 is

 $\left( x~+~2y~+~3z~~4 \right)+\lambda \left( 2x~+~y~~z~+~5~ \right)=0$

 $\Rightarrow x\left( 1+2\lambda  \right)+y\left( 2+\lambda  \right)+z\left( 3-\lambda  \right)-4+5\lambda =0----\left( i \right)$

Also, this is perpendicular to the plane 5x + 3y + 6z + 8 = 0.

$5\left( 1+2\lambda  \right)+3\left( 2+\lambda  \right)+6\left( 3-\lambda  \right)=0$  $\left[ \because {{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}+{{c}_{1}}{{c}_{2}}=0 \right]$

 $\Rightarrow 5+\left( 10\lambda  \right)+6+\left( 3\lambda  \right)+18-\left( 6\lambda  \right)=0$

 $\Rightarrow \lambda =\frac{-29}{7}$

From Eq.(i),

 $x\left( 1+2\left( \frac{-29}{7} \right) \right)+y\left( 2-\frac{29}{7} \right)+z\left( 3+\frac{29}{7} \right)-4+5\left( \frac{-29}{7} \right)=0$

 $\Rightarrow x\left( 7-58 \right)+y\left( 14-29 \right)+z\left( 29+21 \right)-28-145=0$

 $\Rightarrow -51x-15y+50z-173=0$

So the required equation of plane is $51x+15y-50z+173=0$

23.  The plane ax + by = 0 is rotated about its line of intersection with the plane z = 0 through an angle α. Prove that the equation of the plane in its new position is ax + by ±  $\left( \sqrt{{{a}^{2}}+{{b}^{2}}}tan~\alpha  \right)$z = 0.

Ans: Equation of the plane is ax+ by =0 -----(i)

Equation of the plane after new position is

 $\frac{ax~cos~\alpha }{\sqrt{{{a}^{2}}+{{b}^{2}}}}+\frac{by~cos~\alpha }{\sqrt{{{b}^{2}}+{{a}^{2}}}}\pm z~sin~\alpha =0$

$\Rightarrow \frac{ax}{\sqrt{{{a}^{2}}+{{b}^{2}}}}+\frac{by}{\sqrt{{{b}^{2}}+{{a}^{2}}}}\pm z~tan~\alpha =0$       [On dividing by cos $\alpha $ ]

$\Rightarrow ax+by\pm z~tan~\alpha .\sqrt{{{a}^{2}}+{{b}^{2}}}=0$ [On multiplying by $\sqrt{{{a}^{2}}+{{b}^{2}}}$ ]

24. Find the equation of the plane through the intersection of the planes  $\overrightarrow{{{r}_{{}}}}.\left( \hat{i}+3\hat{j} \right)-6=0$and $\overrightarrow{{{r}_{{}}}}.\left( 3\hat{i}-\hat{j}-4\hat{k} \right)=0$, whose perpendicular distance from origin is unity.

Ans: We have, $\overrightarrow{{{n}_{1}}}.\left( \hat{i}+3\hat{j} \right).{{d}_{1}}=6$ and $\overrightarrow{{{n}_{2}}}.\left( 3\hat{i}-\hat{j}-4\hat{k} \right).{{d}_{2}}=0$

Using the relation  $\vec{r}.\left( \overrightarrow{{{n}_{1}}}+\overrightarrow{\lambda {{n}_{2}}} \right)={{d}_{1}}+\lambda {{d}_{2}}$

 $\Rightarrow \overrightarrow{{{r}_{{}}}}.\left[ \left( \hat{i}+3\hat{j} \right)+\lambda \left( 3\hat{i}-\hat{j}-4\hat{k} \right) \right]=6+0.\lambda $

 $\Rightarrow \overrightarrow{{{r}_{{}}}}.\left[ \left( 1+3\lambda  \right)\hat{i}+\left( 3-\lambda  \right)\hat{j}-4\lambda \hat{k} \right]=6---\left( i \right)$

On dividing both sides by $\sqrt{{{(1+3\lambda )}^{2}}+{{(3-\lambda )}^{2}}+{{(-4\lambda )}^{2}}},~we~get$

 $\frac{\overrightarrow{{{r}_{{}}}}.\left[ \left( 1+3\lambda  \right)\hat{i}+\left( 3-\lambda  \right)\hat{j}-4\lambda \hat{k} \right]}{\sqrt{{{(1+3\lambda )}^{2}}+{{(3-\lambda )}^{2}}+{{(-4\lambda )}^{2}}}}=\frac{6}{\sqrt{{{(1+3\lambda )}^{2}}+{{(3-\lambda )}^{2}}+{{(-4\lambda )}^{2}}}}$

Since, the perpendicular distance from origin is unity.

 $\Rightarrow \frac{6}{\sqrt{{{(1+3\lambda )}^{2}}+{{(3-\lambda )}^{2}}+{{(-4\lambda )}^{2}}}}=1$

 $\Rightarrow 36={{(1+3\lambda )}^{2}}+{{(3-\lambda )}^{2}}+{{(-4\lambda )}^{2}}$

 $\Rightarrow 1+9{{\lambda }^{2}}+6\lambda +9+{{\lambda }^{2}}-6\lambda +16{{\lambda }^{2}}=36$

 $\Rightarrow 26{{\lambda }^{2}}+10=36$

 $\Rightarrow \lambda =\pm 1$

Using Eq.(i), the required equation of plane is

 $\overrightarrow{{{r}_{{}}}}.\left[ \left( 1\pm 3 \right)\hat{i}+\left( 3\mp  \right)\hat{j}\mp 4\hat{k} \right]=6$

 $\Rightarrow \overrightarrow{{{r}_{{}}}}.\left[ \left( 1+3 \right)\hat{i}+\left( 3-1 \right)\hat{j}-4\hat{k} \right]=6$

And $\overrightarrow{{{r}_{{}}}}.\left[ \left( 1-3 \right)\hat{i}+\left( 3+1 \right)\hat{j}+4\hat{k} \right]=6$

 $\Rightarrow \overrightarrow{{{r}_{{}}}}.\left[ \left( 4 \right)\hat{i}+2\hat{j}-4\hat{k} \right]=6$

And $\overrightarrow{{{r}_{{}}}}.\left[ -3\hat{i}+4\hat{j}+4\hat{k} \right]=6$

 $\Rightarrow 4x+2y-4z-6=0$

And $-2x+4y+4z-6=0$

25. Show that the points \[\left( \widehat{i}-\widehat{j}+3\widehat{k} \right)\] and \[3\left( \widehat{i}+\widehat{j}+\widehat{k} \right)\] are equidistant from the plane \[\overrightarrow{r}\left[ 5\widehat{i}+2\widehat{j}-7\widehat{k} \right]+9=0\] and lies on the opposite side of it.

Ans: To show that these given points $\left( \hat{i}-\hat{j}+3\hat{k} \right)$ and $3\left( \hat{i}+\hat{j}+\hat{k} \right)$ are equidistant from the plane $\overrightarrow{{{r}_{{}}}}.\left[ 5\hat{i}+2\hat{j}-7\hat{k} \right]+9=0$. We first find out the midpoint of the points which is $\left( 2\hat{i}+\hat{j}+3\hat{k} \right)$.

On substituting $\overrightarrow{{{r}_{{}}}}$ by the midpoint in plane, we get

 $LHS=\left( 2\hat{i}+\hat{j}+3\hat{k} \right).\left( 5\hat{i}+2\hat{j}-7\hat{k} \right)+9$

 $=10+2-21+9=0=RHS$

Hence, the two points lie on opposite sides of the plane are equidistant from the plane.

26. \[\overrightarrow{AB}=\left( 3\widehat{i}-\widehat{j}+\widehat{k} \right)\] and \[\overrightarrow{CD}=\left( -3\widehat{i}+2\widehat{j}+4\widehat{k} \right)\] are two vectors. The position vectors of the points A and C are \[\left( 6\widehat{i}+7\widehat{j}+4\widehat{k} \right)\] and  \[\left( -9\widehat{j}+2\widehat{k} \right)\] respectively. Find the position vector of a point P on the line AB and a point Q on the line CD such that $\overrightarrow{\text{PQ}}$  is perpendicular to $\overrightarrow{\text{AB}}$  and $\overrightarrow{\text{CD}}$  both.

Ans: We have $\overrightarrow{AB}=\left( 3\hat{i}-\hat{j}+\hat{k} \right)$and $\overrightarrow{CD}=\left( -3\hat{i}+2\hat{j}+4\hat{k} \right)$

Also, the position vectors of A and C are $\left( 6\hat{i}+7\hat{j}+4\hat{k} \right)$ and  $\left( -9\hat{j}+2\hat{k} \right)$, respectively. Since,

$\overrightarrow{PQ}$  is perpendicular to $\overrightarrow{AB}$  and $\overrightarrow{CD}$  both.

So, P and Q will be foot of perpendicular to both the lines through A and C.

Now, equation of the line through A and parallel to vector  $\overrightarrow{AB}$ is,

 $\vec{r}=\left( 6\hat{i}+7\hat{j}+4\hat{k} \right)+\lambda \left( 3\hat{i}-\hat{j}+\hat{k} \right)---\left( i \right)$

And equation of the line through C and parallel to vector  $\overrightarrow{CD}$ is,

 $\vec{r}=\left( -9\hat{j}+2\hat{k} \right)+\mu \left( -3\hat{i}+2\hat{j}+4\hat{k} \right)----\left( ii \right)$

Let P $\left( 6+3\lambda ,~7-\lambda ,~4+\lambda  \right)$ is any point on the first line and Q be any point on second line is given by $\left( -3\mu ,~-9+2\mu ,~2+4\mu  \right)$

 $\overrightarrow{PQ}=\left( -3\mu -6-3\lambda  \right)\hat{i}+\left( -9+2\mu -7+\lambda  \right)\hat{j}+\left( 2+4\mu -4-\lambda  \right)\hat{k}$

 $=\left( -3\mu -6-3\lambda  \right)\hat{i}+\left( -16+2\mu +\lambda  \right)\hat{j}+\left( 4\mu -2-\lambda  \right)\hat{k}$

If $\overrightarrow{PQ}$ is perpendicular to the first line, then

 $\left( -3\mu -6-3\lambda  \right)3-\left( -16+2\mu +\lambda  \right)+\left( 4\mu -2-\lambda  \right)=0$

 $\Rightarrow \left( -9\mu -18-9\lambda  \right)+\left( 16-2\mu -\lambda  \right)+\left( 4\mu -2-\lambda  \right)=0$

 $\Rightarrow \left( -7\mu -11\lambda -4 \right)=0---\left( iii \right)$

If $\overrightarrow{PQ}$ is perpendicular to the second line, then

 $\left( -3\mu -6-3\lambda  \right)\left( -3 \right)+2\left( -16+2\mu +\lambda  \right)+4\left( 4\mu +2-\lambda  \right)=0$

 $\Rightarrow \left( 9\mu +18+9\lambda  \right)-32+4\mu +2\lambda +16\mu +8-4\lambda =0$

 $\Rightarrow \left( 29\mu +7\lambda -22 \right)=0---\left( iv \right)$

On solving Eqs. (iii) and (iv), we get

$\left( -49\mu -77\lambda -28 \right)=0$ &  $\left( 319\mu +77\lambda -242 \right)=0$

 $\Rightarrow 270\mu +0-270=0$

 $\Rightarrow \mu =1$

Using $\mu $ in Eq (iii), we get

 $-7\left( 1 \right)-11\lambda -4=0$

 $\Rightarrow -11-11\lambda =0$

 $\Rightarrow \lambda =-1$

So,$\overrightarrow{PQ}=\left( -3\left( 1 \right)-6-3\left( -1 \right) \right)\hat{i}+\left( -16+2\left( 1 \right)-1 \right)\hat{j}+\left( 4\left( 1 \right)-2+1 \right)\hat{k}$

$\overrightarrow{PQ}=-6\hat{i}-15\hat{j}+3\hat{k}$

27.  Show that the straight lines whose direction cosines are given by $2l~+~2m~~n~=~0$ and $mn~+~nl~+~lm~=~0$ are at right angles.

Ans: We have, $2l~+~2m~~n~=~0---\left( i \right)$ 

And $mn~+~nl~+~lm~=~0~---\left( ii \right)$

Eliminating m from both the equations, we get

$m=\frac{n-2l}{2}~$                               [From Eq(i)]

 $\Rightarrow \left( \frac{n-2l}{2} \right)n+nl+l\left( \frac{n-2l}{2} \right)=0$

 $\Rightarrow \frac{{{n}^{2}}-2nl+2nl+nl-2{{l}^{2}}}{2}=0$

 $\Rightarrow {{n}^{2}}+nl-2{{l}^{2}}=0$

 $\Rightarrow {{n}^{2}}+2nl-nl-2{{l}^{2}}=0$

 $\Rightarrow \left( n+2l \right)\left( n-l \right)=0$

 $\Rightarrow n=-2l~~\And ~~n=l$

So, $m=\frac{-2l-2l}{2}~\And ~m=\frac{l-2l}{2}$

 $\Rightarrow m=-2l~~\And ~~m=\frac{-l}{2}$

Thus, the direction ratios of two lines are proportional to $l,-2l,-2$ and $l,\frac{-l}{2},l$.

$\Rightarrow 1,-2,-2$ and $1,\frac{-1}{2},1$

$\Rightarrow 1,-2,-2$ and $2,-1,2$

Also, the vectors parallel to these lines are $\vec{a}=\left( \hat{i}-2\hat{j}-2\hat{k} \right)$ and $\vec{b}=\left( 2\hat{i}-\hat{j}+2\hat{k} \right)$ respectively.

So, $cos~\theta =\frac{\vec{a}~.~\vec{b}}{\left| {\vec{a}} \right|\left| {\vec{b}} \right|}$

 $cos~\theta =\frac{\left( \hat{i}-2\hat{j}-2\hat{k} \right)~.~\left( 2\hat{i}-\hat{j}+2\hat{k} \right)}{3~\times ~3}$

 $cos~\theta =\frac{2+2-4}{9}=0$

So, $\theta ={{90}^{\circ }}$                [∵ cos ${{90}^{\circ }}$= 0 ]

28. If ${{l}_{1}},{{m}_{1}},{{n}_{1}};{{l}_{2}},{{m}_{2}},{{n}_{2}};{{l}_{3}},{{m}_{3}},{{n}_{3}}$ are the direction cosines of three mutually perpendicular lines, prove that the line whose direction cosines are proportional to ${{l}_{1}}+{{l}_{2}}+{{l}_{3}},{{m}_{1}}+{{m}_{2}}+{{m}_{3}},{{n}_{1}}+{{n}_{2}}+{{n}_{3}}$ makes equal angles with them. 

Ans: Let 

 $\vec{a}={{l}_{1}}\hat{i}+{{m}_{1}}\hat{j}+{{n}_{1}}\hat{k}$

 $\vec{b}={{l}_{2}}\hat{i}+{{m}_{2}}\hat{j}+{{n}_{2}}\hat{k}$

 $\vec{c}={{l}_{3}}\hat{i}+{{m}_{3}}\hat{j}+{{n}_{3}}\hat{k}$

 $\vec{d}=\left( {{l}_{1}}+{{l}_{2}}+{{l}_{3}} \right)\hat{i}+\left( {{m}_{1}}+{{m}_{2}}+{{m}_{3}} \right)\hat{j}+\left( {{n}_{1}}+{{n}_{2}}+{{n}_{3}} \right)\hat{k}$

Also, let $\alpha ,\beta $ and $\gamma $ are the angles between $\vec{a}$ and $\vec{d}$ , $\vec{b}$ and $\vec{d}$ , $\vec{c}$ and $\vec{d}$.

So, $cos~\alpha =\left( {{l}_{1}}+{{l}_{2}}+{{l}_{3}} \right){{l}_{1}}+\left( {{m}_{1}}+{{m}_{2}}+{{m}_{3}} \right){{m}_{1}}+\left( {{n}_{1}}+{{n}_{2}}+{{n}_{3}} \right){{n}_{1}}$

 $={{l}_{1}}^{2}+{{l}_{1}}{{l}_{2}}+{{l}_{1}}{{l}_{3}}+{{m}_{1}}^{2}+{{m}_{1}}{{m}_{2}}+{{m}_{1}}{{m}_{3}}+{{n}_{1}}^{2}+{{n}_{1}}{{n}_{2}}+{{n}_{1}}{{n}_{3}}$

 $=\left( {{l}_{1}}^{2}+{{m}_{1}}^{2}+{{n}_{1}}^{2} \right)+\left( {{l}_{1}}{{l}_{2}}+{{l}_{1}}{{l}_{3}}+{{m}_{1}}{{m}_{2}}+{{m}_{1}}{{m}_{3}}+{{n}_{1}}{{n}_{2}}+{{n}_{1}}{{n}_{3}} \right)$

$=1+0=1$           $\left[ \because ~{{l}_{1}}^{2}+{{m}_{1}}^{2}+{{n}_{1}}^{2}=1~and~{{l}_{1}}\bot {{l}_{2}},{{l}_{1}}\bot {{l}_{3}},{{m}_{1}}\bot {{m}_{2}},{{m}_{1}}\bot {{m}_{3}},{{n}_{1}}\bot {{n}_{2}},{{n}_{1}}\bot {{n}_{3}} \right]$

Similarly, $cos~\beta =\left( {{l}_{1}}+{{l}_{2}}+{{l}_{3}} \right){{l}_{2}}+\left( {{m}_{1}}+{{m}_{2}}+{{m}_{3}} \right){{m}_{2}}+\left( {{n}_{1}}+{{n}_{2}}+{{n}_{3}} \right){{n}_{2}}$

 $={{l}_{2}}^{2}+{{l}_{1}}{{l}_{2}}+{{l}_{2}}{{l}_{3}}+{{m}_{2}}^{2}+{{m}_{1}}{{m}_{2}}+{{m}_{2}}{{m}_{3}}+{{n}_{2}}^{2}+{{n}_{1}}{{n}_{2}}+{{n}_{2}}{{n}_{3}}$

 $=\left( {{l}_{2}}^{2}+{{m}_{2}}^{2}+{{n}_{2}}^{2} \right)+\left( {{l}_{1}}{{l}_{2}}+{{l}_{2}}{{l}_{3}}+{{m}_{1}}{{m}_{2}}+{{m}_{2}}{{m}_{3}}+{{n}_{1}}{{n}_{2}}+{{n}_{2}}{{n}_{3}} \right)$

$=1+0=1$           $\left[ \because ~{{l}_{2}}^{2}+{{m}_{2}}^{2}+{{n}_{2}}^{2}=1~and~{{l}_{1}}\bot {{l}_{2}},{{l}_{2}}\bot {{l}_{3}},{{m}_{1}}\bot {{m}_{2}},{{m}_{2}}\bot {{m}_{3}},{{n}_{1}}\bot {{n}_{2}},{{n}_{2}}\bot {{n}_{3}} \right]$

Also, $cos~\gamma =1$ 

 $\Rightarrow cos~\alpha =cos~\beta =cos~\gamma $

 $\Rightarrow \alpha =\beta =\gamma $

S0, the line whose direction cosines are proportional to ${{l}_{1}}+{{l}_{2}}+{{l}_{3}},{{m}_{1}}+{{m}_{2}}+{{m}_{3}},{{n}_{1}}+{{n}_{2}}+{{n}_{3}}$ make equal angles with the three mutually perpendicular lines whose direction cosines are ${{l}_{1}},{{m}_{1}},{{n}_{1}};{{l}_{2}},{{m}_{2}},{{n}_{2}};{{l}_{3}},{{m}_{3}},{{n}_{3}}$ respectively.

Objective Type Questions

Choose the correct answer from the given four options in each of the Exercises from 29 to 36.

29. Distance of the point (α,β,γ) from y-axis is :

(A) β 

(B) |β| 

(C) $\left| \beta  \right|+\left| \gamma  \right|$

(D) $\sqrt{{{\alpha }^{2}}+{{\gamma }^{2}}}$

Ans: The coordinate of the y-axis will be $\left( 0,\beta ,0 \right)$

So the distance of this point  (α,β,γ) from the $\left( 0,\beta ,0 \right)$ is : $\sqrt{{{\left( \alpha -0 \right)}^{2}}+\left( \beta -\beta  \right)+{{\left( \gamma -0 \right)}^{2}}}=\sqrt{{{\alpha }^{2}}+{{\gamma }^{2}}}$

Thus option D is the correct option.

30.  If the directions cosines of a line are k,k,k, then :

(A) k>0 

(B) 0<k<1 

(C) k=1 

(D) $k=\frac{1}{\sqrt{3}~}or~\frac{-1}{\sqrt{3}~}$

Ans: Since we know that ${{l}^{2}}+{{m}^{2}}+{{n}^{2}}=1$

The Dc’s of the line are are k,k,k then $l=k,~m=k,~n=k$

 ${{l}^{2}}+{{m}^{2}}+{{n}^{2}}=1\Rightarrow {{k}^{2}}+{{k}^{2}}+{{k}^{2}}=1$

 $\Rightarrow 3{{k}^{2}}=1$

 $\Rightarrow k=\frac{1}{\sqrt{3}},{{\frac{-1}{\sqrt{3}}}^{{}}}$

Thus the option D is the correct answer.

31. The distance of the plane $\underset{\scriptscriptstyle-}{r}.\left( \frac{2}{7}\hat{i}+\frac{3}{7}\hat{j}-\frac{6}{7}\hat{k} \right)=1$ from the origin is.

(A) 1 

(B) 7 

(C) $\frac{1}{7}$

(D) None of these

Ans: Since we know the equation of a plane as $\underset{\scriptscriptstyle-}{r}.\underset{\scriptscriptstyle-}{n}=d$where d is the distance of the plane from origin. Now on comparing the given equation of plane with the general equation the distance is 1.

Hence option A is the correct answer.

32. The sine of the angle between the straight line $\frac{\text{x-2}}{\text{3}}\text{=}\frac{\text{y-3}}{\text{4}}\text{=}\frac{\text{z-4}}{\text{5}}$and the plane 2x – 2y + z = 5 is

(A) $\frac{\text{10}}{\text{6}\sqrt{\text{5}}}$

(B) $\frac{\text{4}}{\text{5}\sqrt{\text{2}}}$

(C) $\frac{\text{2}\sqrt{\text{3}}}{\text{5}}$

(D) $\frac{\sqrt{\text{2}}}{\text{10}}$

Ans: We know that angle b/w a line and plane is $sin\theta =\frac{\underset{\scriptscriptstyle-}{b}.\underset{\scriptscriptstyle-}{n}}{|\underline{b\left| . \right|\underline{n|}}}$----(1)

The normal vector to the plane is $2\hat{i}-2\hat{j}+\hat{k}$and the vector parallel to the given line is $3\hat{i}+4\hat{j}+5\hat{k}$

Now putting all these values in eq. (i)

 $sin\theta =\frac{\left( 2\hat{i}-2\hat{j}+\hat{k} \right)\left( 3\hat{i}+4\hat{j}+5\hat{k} \right)}{\sqrt{{{2}^{2}}+{{2}^{2}}+1}\sqrt{{{3}^{2}}+{{4}^{2}}+{{5}^{2}}}}$

 $sin\theta =\frac{6-8+5}{3\times 5\sqrt{2}}=\frac{3}{15\sqrt{2}}=\frac{1}{5\sqrt{2}}$

 $sin\theta =\frac{\sqrt{2}}{10}$

Thus, option D is the correct answer.

33.  The reflection of the point (α,β,γ) in the xy– plane is 

(A) (α,β,0) 

(B) (0,0,γ) 

(C) (–α,–β,γ) 

(D) (α,β,–γ)

Ans: The reflection of a point (a,b,c) in XY-plane is (a,b,-c)

Thus the reflection of point  (α,β,γ) is  (α,β, -γ)

Hence, Option D is the correct answer.

34. The area of the quadrilateral ABCD, where A(0,4,1), B (2, 3, –1), C(4, 5, 0) and D (2, 6, 2), is equal to 

(A) 9 sq. units 

(B) 18 sq. units 

(C) 27 sq. units 

(D) 81 sq. units

Ans: Vectors of the sides of quadrilateral are:

 $\underline{AB}=\left( 2-0 \right)\hat{i}+\left( 3-4 \right)\hat{j}+\left( -1-1 \right)\hat{k}=2\hat{i}-\hat{j}-2\hat{k}$

 $\underline{BC}=\left( 4-2 \right)\hat{i}+\left( 5-3 \right)\hat{j}+\left( 0+1 \right)\hat{k}=2\hat{i}+\widehat{2j}+\hat{k}$

 $\underline{CD}=\left( 2-4 \right)\hat{i}+\left( 6-5 \right)\hat{j}+\left( 2-0 \right)\hat{k}=-2\hat{i}+\hat{j}+2\hat{k}$

 $\underline{DA}=\left( 0-2 \right)\hat{i}+\left( 4-6 \right)\hat{j}+\left( 1-2 \right)\hat{k}=-2\hat{i}-2\hat{j}-\hat{k}$

The area of quadrilateral ABCD is \[\left| \overline{AB}\times \overline{CD} \right|=\left| \begin{matrix}

   \widehat{i} & \widehat{j} & \widehat{k}  \\

   2 & -1 & -2  \\

   2 & 2 & 1  \\

\end{matrix} \right|\]

 $\left| \underline{AB}\times \underline{BC} \right|=\hat{i}\left( -1+4 \right)-\left( 2+4 \right)\hat{j}+\hat{k}\left( 4+2 \right)$

 $\left| \underline{AB}\times \underline{BC} \right|=3\hat{i}-6\hat{j}+6\hat{k}=\sqrt{9+36+36}=9sq.~units$

Thus, option A is the correct answer.

35.  The locus represented by xy + yz = 0 is 

(A) A pair of perpendicular lines 

(B) A pair of parallel lines 

(C) A pair of parallel planes 

(D) A pair of perpendicular planes

Ans: Given, xy + yz = 0

 $\Rightarrow xy=-yz$

This represents the equation of perpendicular planes.

36.  The plane 2x – 3y + 6z – 11 = 0 makes an angle $si{{n}^{1}}\left( \alpha  \right)$with x-axis. The value of α is equal to

(A) $\frac{\sqrt{\text{3}}}{\text{2}}$

(B) $\frac{\sqrt{\text{2}}}{\text{3}}$

(C) $\frac{\text{2}}{\text{7}}$

(D) $\frac{\text{3}}{\text{7}}$

Ans: The vector parallel to x-axis is $\underset{\scriptscriptstyle-}{b}=\hat{i}+0\hat{j}+0\hat{k}$

The normal vector to the plane is $\underset{\scriptscriptstyle-}{n}=2\hat{i}-3\hat{j}+6k\widehat{{}}$

Now the angle b/w the x-axis and the given plane is $sin\theta =\frac{\underset{\scriptscriptstyle-}{n}.\underset{\scriptscriptstyle-}{b}}{\left| \underset{\scriptscriptstyle-}{n}\left| . \right|\underset{\scriptscriptstyle-}{b} \right|}$

 $sin\theta =\frac{\left( \hat{i}+0\hat{j}+0\hat{k} \right).\left( 2\hat{i}-3\hat{j}+6k\widehat{{}} \right)}{1\times \sqrt{4+9+36}}=\frac{2}{7}$

 $\Rightarrow sin\left[ si{{n}^{1}}\left( \alpha  \right) \right]=\frac{\left( \hat{i}+0\hat{j}+0\hat{k} \right).\left( 2\hat{i}-3\hat{j}+6k\widehat{{}} \right)}{1\times \sqrt{4+9+36}}=\frac{2}{7}$

 $\Rightarrow \alpha =\frac{2}{7}$

Thus option C is the correct answer.

Fill in the blanks in each of the Exercises 37 to 41.

37. A plane passes through the points (2,0,0) (0,3,0) and (0,0,4). The equation of the plane is __________.

Ans: The equation of plane which cuts the coordinate axes at  (2,0,0) (0,3,0) and (0,0,4) is $\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\Rightarrow \frac{x}{2}+\frac{y}{3}+\frac{z}{4}=1$

Thus the equation of plane is $\frac{x}{2}+\frac{y}{3}+\frac{z}{4}=1$

38.  The direction cosines of the vector $\left( 2\hat{i}+2\hat{j}-\hat{k} \right)$ are __________.

Ans: The direction cosines of the vector $\left( 2\hat{i}+2\hat{j}-\hat{k} \right)$are $\frac{2}{\sqrt{{{2}^{2}}+{{2}^{2}}+1}},\frac{2}{\sqrt{{{2}^{2}}+{{2}^{2}}+1}},\frac{-1}{\sqrt{{{2}^{2}}+{{2}^{2}}+1}}\Rightarrow \frac{2}{3},\frac{2}{3},\frac{-1}{3}$

39.  The vector equation of the line $\frac{x-5}{3}=\frac{y+4}{7}=\frac{z-6}{2}$is __________.

Ans: The DR’s of the line is 3,7,2 and the point is (5,-4,6)

The vector equation of the plane is $\underset{\scriptscriptstyle-}{r}=\left( 5\hat{i}-4\hat{j}+6\hat{k} \right)+\lambda \left( 3\hat{i}+7\hat{j}+2\hat{k} \right)$

40.  The vector equation of the line through the points (3,4,–7) and (1,–1,6) is __________. 

Ans: Let $\underset{\scriptscriptstyle-}{r}=x\hat{i}+y\hat{j}+z\hat{k}$and $\underset{\scriptscriptstyle-}{a}=3\hat{i}+4\hat{j}-7\hat{k}$and $\underset{\scriptscriptstyle-}{b}=\hat{i}-\hat{j}+6\hat{k}$

The equation of line passing through two points is $\underset{\scriptscriptstyle-}{r}=\underset{\scriptscriptstyle-}{a}+\lambda (\underset{\scriptscriptstyle-}{b}-\underline{a)}$

 $\underset{\scriptscriptstyle-}{r}=\left( 3\hat{i}+4\hat{j}-7\hat{k} \right)+\lambda \left[ \left( 1-3 \right)\hat{i}+\left( -1-4 \right)\hat{j}+\left( 6+7 \right)\hat{j} \right]$

 $\Rightarrow \underset{\scriptscriptstyle-}{r}=\left( 3\hat{i}+4\hat{j}-7\hat{k} \right)+\lambda \left[ -2\hat{i}-5\hat{j}+13\hat{j} \right]$

 $\Rightarrow x\hat{i}+y\hat{j}+z\widehat{k=}\left( 3\hat{i}+4\hat{j}-7\hat{k} \right)+\lambda \left[ -2\hat{i}-5\hat{j}+13\hat{j} \right]$

 $\Rightarrow \left( x-3 \right)\hat{i}+\left( y-4 \right)\hat{j}+\left( z+7 \right)\hat{k}=\lambda \left( -2\hat{i}-5\hat{j}+13\hat{j} \right)$

41. The cartesian equation of the plane $\underset{\scriptscriptstyle-}{r}.\left( \hat{i}+\hat{j}-\hat{k} \right)=2$is  __________.

Ans: Let $\underset{\scriptscriptstyle-}{r}=x\hat{i}+y\hat{j}+z\hat{k}$

 $(x\hat{i}+y\hat{j}+z\widehat{k).\left( \hat{i}+\hat{j}-\hat{k} \right)=2}$

 $\Rightarrow x+y-z=2$

Thus the required form is $x+y-z=2$.

State True or False for the statements in each of the Exercises 42 to 49.

42. The unit vector normal to the plane x + 2y +3z – 6 = 0 is $\frac{1}{\sqrt{14}}i\widehat{{}}+\frac{2}{\sqrt{14}}\hat{j}+\frac{3}{\sqrt{14}}\hat{k}$

Ans: The normal vector to the plane is $\underset{\scriptscriptstyle-}{n}=i\widehat{{}}+2\hat{j}+3\hat{k}$.

Now the unit vector is $\hat{n}=\frac{i\widehat{{}}+2\hat{j}+3\hat{k}}{\sqrt{1+{{2}^{2}}+{{3}^{2}}}}=\frac{1}{\sqrt{14}}i\widehat{{}}+\frac{2}{\sqrt{14}}\hat{j}+\frac{3}{\sqrt{14}}\hat{k}$

Thus the given statement is True.

43.  The intercepts made by the plane 2x – 3y + 5z +4 = 0 on the coordinate axis are $-2,~\frac{4}{3},\frac{-4}{5}$.

Ans: Given, The equation of plane 2x – 3y + 5z +4 = 0

 $\Rightarrow 2x~~3y~+~5z=-4$

 $\Rightarrow \frac{2x}{-4}~+\frac{~3y}{4}~+~\frac{5z}{-4}=1$

 $\Rightarrow \frac{x}{-2}~+\frac{~y}{\frac{4}{3}}~+~\frac{z}{\frac{-4}{5}}=1$

Thus the given statement is True.

44. The angle between the line \[\underline{r}=\left( 5\widehat{i}-\widehat{j}-4\widehat{k} \right)+\lambda \left( 2\widehat{i}-\widehat{j}+\widehat{k} \right)\] and the plane \[\underline{r}\left( 3\widehat{i}-4\widehat{j}-\widehat{k} \right)+5=0\] is \[{{\sin }^{-1}}\left( \frac{5}{2\sqrt{91}} \right)\]

Ans: We have $\underset{\scriptscriptstyle-}{b}=2\hat{i}-\hat{j}+\hat{k}$and $\underset{\scriptscriptstyle-}{n}=3\hat{i}-4\hat{j}-\hat{k}$

The angle b/w a line and plane is $Sin\theta =\frac{\underset{\scriptscriptstyle-}{b}.\underset{\scriptscriptstyle-}{n}}{\left| \underset{\scriptscriptstyle-}{b}\left| . \right|\underset{\scriptscriptstyle-}{n} \right|}=\frac{6+4-1}{\sqrt{{{2}^{2}}+1+1}.\sqrt{{{3}^{2}}+{{4}^{2}}+1}}=\frac{9}{\sqrt{6}.\sqrt{26}}=\frac{9}{2\sqrt{39}}$

 $\theta =si{{n}^{-1}}\left( \frac{9}{2\sqrt{39}} \right)$

Thus the statement is false.

45. The angle between the planes \[\underline{r}=\left( 2\widehat{i}-3\widehat{j}+\widehat{k} \right)=1\] and \[\underline{r}\left( \widehat{i}-\widehat{j} \right)=4\] is $\text{co}{{\text{s}}^{\text{-1}}}\left( \frac{\text{-5}}{\sqrt{\text{58}}} \right)$.

Ans: The angle b/w two planes is $cos\theta =\frac{{{n}_{1}}.{{n}_{2}}}{\left| {{n}_{1}} \right|\left| {{n}_{2}} \right|}$

${{n}_{1}}=2\hat{i}-3\hat{j}+\hat{k}$and ${{n}_{2}}=\hat{i}-\hat{j}$

So, $cos\theta =\frac{2+3}{\sqrt{4+9+1}.\sqrt{1+1}}=\frac{5}{2\sqrt{7}}$

 $\theta =co{{s}^{-1}}\left( \frac{5}{2\sqrt{7}} \right)$

Thus the statement is False.

46.  The line \[\underline{r}=2\widehat{i}-3\widehat{j}-\widehat{k}+\lambda \left( \widehat{i}-\widehat{j}+2\widehat{k} \right)\] lies in the plane \[\underline{r}\left( 3\widehat{i}+\widehat{j}-\widehat{k} \right)+2=0\].

Ans: Let $\underset{\scriptscriptstyle-}{r}=x\hat{i}+y\hat{j}+z\hat{k}$

Now, $x\hat{i}+y\hat{j}+z\hat{k}=\left( 2+\lambda  \right)\hat{i}+\left( -3+-\lambda  \right)\hat{j}+\left( -1+2\lambda  \right)\hat{k}$

The general point is [$\left( 2+\lambda  \right),-\left( 3+\lambda  \right),-\left( 1+2\lambda  \right)$] . If the line lies on the plane then this point must satisfy the plane.

 $\underset{\scriptscriptstyle-}{r}.\left( 3\hat{i}+\hat{j}-\hat{k} \right)+2=\left[ \left( 2+\lambda  \right)\hat{i}+\left( -3+-\lambda  \right)\hat{j}+\left( -1+2\lambda  \right)\hat{k} \right].\left( 3\hat{i}+\hat{j}-\hat{k} \right)+2$

 $~~~~~~~~~~~~~~~~~~~~~~~~~~=6+3\lambda -3-\lambda +1-2\lambda +2=6\ne 0$

Thus the Statement is False.

47. The vector equation of the line $\frac{\text{x-5}}{\text{3}}\text{=}\frac{\text{y+4}}{\text{7}}\text{=}\frac{\text{z-6}}{\text{2}}$ is \[\underline{r}=5\widehat{i}-4\widehat{j}+6\widehat{k}+\lambda \left( 3\widehat{i}+7\widehat{j}+2\widehat{k} \right)\]

Ans: The point is (5,-4,6) through which line is passing and the DR’s of the line are 3,7,2 

Now the vector form is $\underset{\scriptscriptstyle-}{r}=\left( 5\hat{i}-4\hat{j}+6\hat{k} \right)+\lambda \left( 3\hat{i}+7\hat{j}+2\hat{k} \right)$

Thus the given statement is True.

48.  The equation of a line, which is parallel to \[2\widehat{i}+\widehat{j}+3\widehat{k}\] and which passes through the point (5,-2,4) is $\frac{\text{x-5}}{\text{2}}\text{=}\frac{\text{y+2}}{\text{-1}}\text{=}\frac{\text{z-4}}{\text{3}}$.

Ans: The line is parallel to $2\hat{i}+\hat{j}+3\hat{k}$ so the DR’s of the line is 2,1,3  and given the point is (5,-2,4). 

So the equation of line is $\frac{x-5}{2}=\frac{y-\left( -2 \right)}{1}=\frac{z-4}{3}\Rightarrow \frac{x-5}{2}=\frac{y+2}{1}=\frac{z-4}{3}$

Therefore the statement is False.

49.  If the foot of perpendicular drawn from the origin to a plane is (5, – 3, – 2), then the equation of plane is \[\underline{r}=\left( 5\widehat{i}-3\widehat{j}-2\widehat{k} \right)=38\].

Ans: Given point (5, – 3, – 2) is on the plane and foot of perpendicular from the point (0,0,0). So the normal vector to the plane is $\underset{\scriptscriptstyle-}{n}=5\hat{i}-3\hat{j}-2\hat{k}$ .

Now the equation of plane is $\left( \underset{\scriptscriptstyle-}{r}-\underset{\scriptscriptstyle-}{a} \right).\underset{\scriptscriptstyle-}{n}=0$

 $\underset{\scriptscriptstyle-}{r}.\underset{\scriptscriptstyle-}{n}=\underset{\scriptscriptstyle-}{a}.\underset{\scriptscriptstyle-}{n}$

 $\Rightarrow \underset{\scriptscriptstyle-}{r}.\left( 5\hat{i}-3\hat{j}-2\hat{k} \right)=\left( 5\hat{i}-3\hat{j}-2\hat{k} \right)\left( 5\hat{i}-3\hat{j}-2\hat{k} \right)$

 $\Rightarrow \underset{\scriptscriptstyle-}{r}.\left( 5\hat{i}-3\hat{j}-2\hat{k} \right)=25+9+4=38$

Thus the given statement is True.

Some Tips for Scoring Good Marks in Exams:

Although there are no full-proof tips or tricks to score good marks in Exams, inoculating some of the below mentioned habits can help one to successfully clear any Examination.

• Preparing revision notes

• Effective time management skills

• Solving multiple worksheets and sample paper

• Attempting mock tests

• Starting the preparatory stage with familiarizing the syllabus

• Consistent revision and practice

• Smart study by focusing on weightage of various topics

• Sleeping enough and having a proper diet