NCERT Exemplar for Class 8 Maths Solutions Chapter 11 Mensuration

Access NCERT Exemplar Solutions for Class 8 Mathematics

Chapter 11 - Mensuration

(Examples, Easy Methods and Step by Step Solutions)

Examples

Example 1: What is the area of the triangle ADE in the following figure?

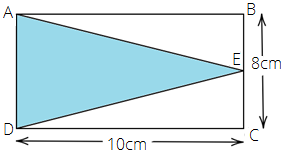
a) $45c{m^2}$

b) $50c{m^2}$

c) $55c{m^2}$

d) $40c{m^2}$

Ans: The correct answer is option (d) $40c{m^2}$

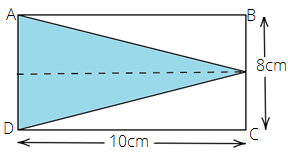
From the above figure, we have

$AD = BC = 8cm$ and $DC = OE = 10cm$

Thus, for the $\vartriangle ADE$ 

Length of the base = $AD$ = $8cm$

Length of height = $OE$= $10cm$

Area of $\vartriangle ADE$ = $\dfrac{1}{2} \times base \times height$ = $\dfrac{1}{2} \times 8 \times 10$ = $40c{m^2}$

Example 2: What will be the change in the volume of a cube when its side becomes $10$times the original side?

a) Volume becomes $1000$ times.

b) Volume becomes $10$ times.

c) Volume becomes $100$ times.

d) Volume becomes $\dfrac{1}{{1000}}$ times.

Ans: The correct answer is option (a) Volume becomes $1000$ times.

Let the side of the cube be $x$

The volume of the cube having side $x$= ${x^3}$

If the side of the cube becomes $10$ times, then the side would be $10x$

The volume of the cube having side $10x$= ${\left( {10x} \right)^3}$ = $1000{x^3}$

Hence, the volume becomes $1000$ times of the original volume. 

Example 3: Area of a rhombus is equal to _____ of its diagonals.

Ans: Half the product

Area of the rhombus = $\dfrac{1}{2} \times {d_1} \times {d_2}$

Example 4: If the area of a face of a cube is $10c{m^2}$, then the total surface area of the cube is _____.

Ans: $60c{m^2}$

Given that, the area of a face of a cube is $10c{m^2}$

We know that the cube has six faces. Therefore, we get

$ \Rightarrow 6 \times 10c{m^2}$ 

$ \Rightarrow 60c{m^2}$

Hence, the total surface area of the cube is $60c{m^2}$.

Example 5: $1L = 1000c{m^3}$

Ans: True

Example 6: Amount of region occupied by a solid is called its surface area.

Ans: False

Example 7: $160{m^3}$ of water is to be used to irrigate a rectangular field whose area is $800{m^2}$. What will be the height of the water level in the field?

Ans: Given that, 

The volume of water = $160{m^3}$

Area of rectangular field = $800{m^2}$

Let the height of water level in the field be $h$

The volume of water = volume of cuboid formed on the field by water.

$ \Rightarrow 160 = Area{\text{ }}of{\text{ }}base \times height$ 

$ \Rightarrow 160 = 800 \times h$

$ \Rightarrow h = \dfrac{{160}}{{800}}$

$ \Rightarrow h = 0.2m$

Hence, the required height is $0.2m$.

Example 8: Find the area of the rhombus whose one side measures $5cm$ and one diagonal as $8cm$

Ans: Let ABCD be a rhombus.

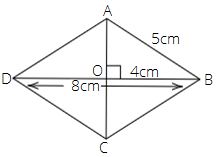
Here, $DO = OB = 4cm$, since diagonals of a rhombus are perpendicular bisectors of each other. 

Therefore, by Pythagoras theorem in $\vartriangle AOB$, we have

$ \Rightarrow {\left( {AO} \right)^2} + {\left( {OB} \right)^2} = {\left( {AB} \right)^2}$ 

$ \Rightarrow {\left( {AO} \right)^2} = {\left( {AB} \right)^2} - {\left( {OB} \right)^2}$

$ \Rightarrow AO = \sqrt {{{\left( 5 \right)}^2} - {{\left( 4 \right)}^2}} $

$ \Rightarrow AO = \sqrt {25 - 16} $

$ \Rightarrow AO = \sqrt 9 $

$ \Rightarrow AO = 3cm$

Thus, $AC = 2 \times 3 = 6cm$

Therefore, area of the rhombus = $\dfrac{1}{2} \times {d_1} \times {d_2}$ = $\dfrac{1}{2} \times 8 \times 6$= $24c{m^2}$

Example 9: The parallel sides of a trapezium are $40cm$ and $20cm$. If its non-parallel sides are both equal, each being $26cm$, find the area of the trapezium.

Ans: Let ABCD be a trapezium, in which $AB = 40cm$ and $CD = 20cm$ and $AD = BC = 26cm$

Now, draw $CL\parallel AD$ 

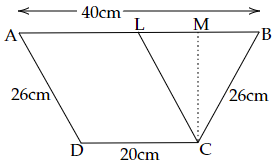
Now, we have parallelogram ALCD

So, $AL = CD = 20cm$ and $CL = AD = 26cm$

In $\vartriangle CLB$, we have

$CL = CB = 26cm$

Thus, $\vartriangle CLB$is an isosceles triangle.

Now, draw altitude CM of $\vartriangle CLB$

Since $\vartriangle CLB$ is an isosceles triangle. So, CM is also the median.

Then, $LM = MB = \dfrac{1}{2}BL$ = $\dfrac{1}{2} \times 20cm$ = $10cm$

(As $BL = AB - AL$ = $\left( {40 - 20} \right)cm = 20cm$ )

Now, apply Pythagoras theorem on $\vartriangle CLM$

$ \Rightarrow {\left( {CL} \right)^2} = {\left( {CM} \right)^2} + {\left( {LM} \right)^2}$ 

$ \Rightarrow {\left( {26} \right)^2} = {\left( {CM} \right)^2} + {\left( {10} \right)^2}$

$ \Rightarrow {\left( {CM} \right)^2} = {\left( {26} \right)^2} - {\left( {10} \right)^2}$

$ \Rightarrow {\left( {CM} \right)^2} = 676 - 100$

$ \Rightarrow {\left( {CM} \right)^2} = 576$

\[ \Rightarrow CM = 24cm\]

Area of trapezium = $\dfrac{1}{2} \times \left( {sum{\text{ }}of{\text{ }}parallel{\text{ }}side} \right) \times height$= $\dfrac{1}{2} \times \left( {20 + 40} \right) \times 24$ = $30 \times 24$ = $720c{m^2}$ 

Example 10: Find the area of polygon ABCDEF, if $AD = 18cm$, $AQ = 14cm$, $AP = 12cm$, $AN = 8cm$, and FM, EP, QC and BN are perpendiculars to diagonal AD.

Ans: 

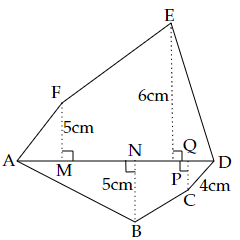
In the figure, we have

$ \Rightarrow MP = AP - AM = \left( {12 - 4} \right)cm = 8cm$ 

$ \Rightarrow PD = AD - AP = \left( {18 - 12} \right)cm = 6cm$

$ \Rightarrow NQ = AQ - AN = \left( {14 - 8} \right)cm = 6cm$

$ \Rightarrow QD = AD - AQ = \left( {18 - 14} \right)cm = 4cm$

Area of the polygon ABCDEF = area of $\vartriangle AFM$ + area of trapezium FMPE + area of $\vartriangle EPD$ + area of $\vartriangle ANB$ + area of trapezium NBCQ + area of $\vartriangle QCD$ 

Area of $\vartriangle AFM$ = $\dfrac{1}{2} \times base \times height$ = AM × FM = $\dfrac{1}{2} \times 4 \times 5$ = $10c{m^2}$

Area of trapezium FMPE = $\dfrac{1}{2} \times \left( {sum{\text{ }}of{\text{ }}parallel{\text{ }}side} \right) \times height$= $\dfrac{1}{2}\left( {FM + EP} \right) \times MP$ = $\dfrac{1}{2} \times \left( {5 + 6} \right) \times 8$ = $11 \times 4$ = $44c{m^2}$ 

Area of $\vartriangle EPD$ = $\dfrac{1}{2} \times base \times height$ = PD × EP = $\dfrac{1}{2} \times 6 \times 6$ = $18c{m^2}$

Area of $\vartriangle ANB$ = $\dfrac{1}{2} \times base \times height$ = AN × NB = $\dfrac{1}{2} \times 8 \times 5$ = $20c{m^2}$

Area of trapezium NBCQ = $\dfrac{1}{2} \times \left( {sum{\text{ }}of{\text{ }}parallel{\text{ }}side} \right) \times height$= $\dfrac{1}{2}\left( {NB \times CQ} \right) \times NQ$ = $\dfrac{1}{2} \times \left( {5 + 4} \right) \times 6$ = $9 \times 3$ = $27c{m^2}$ 

Area of $\vartriangle QCD$ = $\dfrac{1}{2} \times base \times height$ = QD × CQ = $\dfrac{1}{2} \times 4 \times 4$ = $8c{m^2}$

Therefore, area of the polygon ABCDEF = $10c{m^2} + 44c{m^2} + 18c{m^2} + 20c{m^2} + 27c{m^2} + 8c{m^2}$

$ = 127c{m^2}$ 

Exercise

In questions $1$ to $28$, there are four options out of which one is correct. Write the correct answer. 

1. A cube of side $5cm$ is painted on all its faces. If it is sliced into $1$ cubic centimeter cubes, how many $1$ cubic centimeter cubes will have exactly one of their faces painted?

a) $27$

b) $42$

c) $54$

d) $142$

Ans: The correct answer is option (c) $54$ 

Given, a cube of side $5cm$ is painted on all its faces and it is sliced into $1$ cubic centimeter cubes.

Therefore, from the figure, it is clear that there are $9$ cubes available on each face

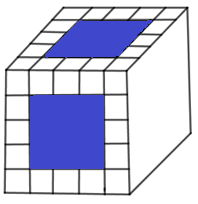
We know that a cube has $6$ faces. Therefore, the total number of cubes = $6 \times 9$ 

$ \Rightarrow 54$ 

2. A cube of side $4cm$ is cut into $1cm$ cubes. What is the ratio of the surface areas of the original cubes and cut-out cubes? 

a) $1:2$

b) $1:3$

c) $1:4$

d) $1:6$

Ans: The correct answer is option (c) $1:4$ 

We know that volume of a cube with side $a$ = ${a^3}$ 

Therefore, the volume of a cube having the side of length $4cm$ = ${\left( 4 \right)^3}$ 

$ = 64c{m^3}$ 

Now, we will find the volume of the cut-out cubes with a side of length $1cm$.

$ = 1c{m^3}$

Therefore, the number of cut-out cubes = Volume of the original cube $ \div $ Volume of a smaller cube. Therefore, we get

$ \Rightarrow \dfrac{{64c{m^3}}}{{1c{m^3}}} = 64$ 

We know that the surface area of the cube with side $a$ = $6{a^2}$ 

Therefore, the surface area of $64$ cut-out cubes = $64 \times 6 \times {1^2}c{m^2}$ 

And, the surface area of the original cube with side $4cm$ = $6 \times {4^2}c{m^2}$ 

Therefore, required ratio = $\dfrac{{6 \times {4^2}}}{{64 \times 6}}$ 

$= \dfrac{{16}}{{64}}$

$= \dfrac{1}{4}$

Therefore, the required ratio is $1:4$.

3. A circle of maximum possible size is cut from a square sheet of board. Subsequently, a square of maximum possible size is cut from the resultant circle. What will be the area of the final square? 

a) $\dfrac{3}{4}$ of original square.

b) $\dfrac{1}{2}$ of original square.

c) $\dfrac{1}{4}$ of original square.

d) $\dfrac{2}{3}$ of original square.

Ans: The correct answer is option (b) $\dfrac{1}{2}$ of original square.

Let the side of a square sheet be $a$ 

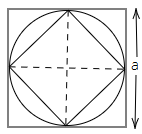
Therefore, the area of the square sheet with side $a$ = ${a^2}........\left( i \right)$ 

Now, we make the circle of the maximum possible size from the square sheet. Then, the radius of the circle = $\dfrac{a}{2}$ 

Therefore, the diameter of the circle will be $a$ 

We know that any square in a circle of maximum size will have the length of diagonal equal to the diameter of the circle. 

Thus, the length of the diagonal of a square made inside the circle = $a$ 

We know that $side \times \sqrt 2  = diagonal$ 

Therefore, side = $\dfrac{a}{{\sqrt 2 }}$ 

Thus, area of square = ${\left( {\dfrac{a}{{\sqrt 2 }}} \right)^2}$

$ = \dfrac{{{a^2}}}{2}.......\left( {ii} \right)$ 

Hence, the area of the final square is $\dfrac{1}{2}$ of the original square.

4. What is the area of the largest triangle that can be fitted into a rectangle of length $l$ units and width $w$ units?

a) $\dfrac{{lw}}{2}$

b) $\dfrac{{lw}}{3}$

c) $\dfrac{{lw}}{6}$

d) $\dfrac{{lw}}{4}$

Ans: The correct answer is option (a) $\dfrac{{lw}}{2}$ 

Let ABCD be the rectangle of length $l$ and width $w$.

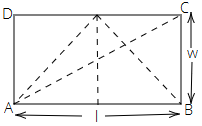
Let us construct a triangle of maximum area inside the rectangle in all possible ways-

Area of rectangle = $\dfrac{1}{2} \times base \times height$ 

Maximum base length = $l$  

Maximum height = $w$ 

Therefore, maximum area of triangle = $\dfrac{1}{2} \times l \times w$ 

$ \Rightarrow \dfrac{{lw}}{2}sq{\text{ }}units$ 

5. If the height of a cylinder becomes $\dfrac{1}{4}$ of the original height and the radius is doubled, then which of the following will be true? 

a) Volume of the cylinder will be doubled. 

b) Volume of the cylinder will remain unchanged. 

c) Volume of the cylinder will be halved. 

d) Volume of the cylinder will be $\dfrac{1}{4}$ of the original volume. 

Ans: The correct answer is option (b) Volume of the cylinder will remain unchanged. 

Volume of cylinder having base radius $r$ and height $h$ is $V$ = $\pi {r^2}h$ 

If the radius is double, we get $r'$ = $2r$ 

The new height, $h'$ = $\dfrac{1}{4}h$ 

So, new volume would be $V'$ = $\pi {\left( {2r} \right)^2} \times \dfrac{1}{4}h$ = $\pi {r^2}h$ = $V$ 

Thus, the new volume of the cylinder is the same as the original volume of the cylinder.

6. If the height of a cylinder becomes $\dfrac{1}{4}$ of the original height and the radius is doubled, then which of the following will be true? 

a) Curved surface area of the cylinder will be doubled. 

b) Curved surface area of the cylinder will remain unchanged. 

c) Curved surface area of the cylinder will be halved. 

d) Curved surface area will be $\dfrac{1}{4}$ of the original curved surface. 

Ans: The correct answer is option (c) Curved surface area of the cylinder will be halved. 

We know that the curved surface area of a cylinder having radius $r$ and height $h$ = $2\pi rh$ 

According to the question, new height is $\dfrac{h}{4}$ and new radius is $2r$ 

Therefore, the curved surface area of the new cylinder = $2\pi  \times 2r \times \dfrac{h}{4}$

$ \Rightarrow 4\pi r \times \dfrac{h}{4}$

$ \Rightarrow \pi rh$

Multiply and divide the above-written expression by $2$ 

$ \Rightarrow \dfrac{1}{2} \times 2\pi rh$

$ = \dfrac{1}{2}$ original curved surface area.

7. If the height of a cylinder becomes $\dfrac{1}{4}$ of the original height and the radius is doubled, then which of the following will be true? 

a) Total surface area of the cylinder will be doubled. 

b) Total surface area of the cylinder will remain unchanged. 

c) Total surface of the cylinder will be halved. 

d) None of the above. 

Ans: The correct answer is option (d) None of the above.

We know that the total surface of the cylinder having radius $r$ and height $h$ = $2\pi r\left( {h + r} \right)$ 

According to the question, new height is $\dfrac{h}{4}$ and new radius is $2r$ 

Therefore, the total surface area of the new cylinder = $2\pi  \times 2r\left( {\dfrac{h}{4} + 2r} \right)$

$= 4\pi r\left( {\dfrac{{h + 8r}}{4}} \right)$

$= \pi r\left( {h + 8r} \right)$

8. The surface area of the three co-terminus faces of a cuboid are $6$, $15$, and $10c{m^2}$ respectively. The volume of the cuboid is 

a) $30c{m^3}$

b) $40c{m^3}$

c) $20c{m^3}$

d) $35c{m^3}$

Ans: The correct answer is option (a) $30c{m^3}$

We know that the volume of the cuboid having dimensions $l$, $b$ and $h$ = $l \times b \times h$.

Here, in the given question, we have

$ \Rightarrow l \times b = 6$, $l \times h = 15$ and $b \times h = 10$

Therefore, we get

$ \Rightarrow {l^2} \times {b^2} \times {h^2} = 6 \times 15 \times 10$ 

Take square root on both the sides

$ \Rightarrow l \times b \times h = \sqrt {6 \times 15 \times 10} $

$ \Rightarrow l \times b \times h = \sqrt {900} $

$ \Rightarrow l \times b \times h = 30c{m^3}$

9. A regular hexagon is inscribed in a circle of radius $r$. The perimeter of the regular hexagon is 

a) $3r$

b) $6r$

c) $9r$

d) $12r$

Ans: The correct answer is option (b) $6r$

We know that each hexagon comprises $6$ equilateral triangles and each of them has one of their vertices at the center of the hexagon. 

The sides of an equilateral triangle are equal to the radius of the smallest circle inscribing the hexagon.

Therefore, each side of the hexagon is equal to the radius of the hexagon.

Hence, the perimeter of the hexagon = $6r$ 

10. The dimensions of a godown are $40m$, $25m$ and $10m$. If it is filled with cuboidal boxes each of dimensions $2m \times 1.25m \times 1m$, then the number of boxes will be

a) $1800$

b) $2000$

c) $4000$

d) $8000$

Ans: The correct answer is option (c) $4000$

Dimensions of the given godown are $40m$, $25m$ and $10m$.

Thus, the volume of godown = $40 \times 25 \times 10{m^3}$ 

$ = 10000{m^3}$

Now, we will find the volume of each cuboidal box.

$= 2 \times 1.25 \times 1{m^3}$ 

$= 2.5{m^3}$

Therefore, the number of boxes that can be filled in the godown = Volume of godown $ \div $ volume of each cuboidal box

$= \dfrac{{10000}}{{2.5}}$ 

$= 4000$

11. The volume of a cube is $64c{m^3}$. Its surface area is 

a) $16c{m^2}$

b) $64c{m^2}$

c) $96c{m^2}$

d) $128c{m^2}$

Ans: The correct answer is option (c) $96c{m^2}$

We know that volume of a cube with side $a$ = ${a^3}$ 

Therefore, according to the question,

$ \Rightarrow {a^3} = 64$ 

On taking cube root, we get

$ \Rightarrow a = 4$

The surface area of a cube with side $a$ = $6{a^2}$ 

$= 6 \times {4^2}$ 

$= 96c{m^2}$

12. If the radius of a cylinder is tripled but its curved surface area is unchanged, then its height will be 

a) Tripled 

b) Constant 

c) one-sixth 

d) one third 

Ans: The correct answer is option (d) one third

Let the new height be $h'$ 

We know that the curved surface area of a cylinder with radius $r$ and height $h$ = $2\pi rh$ 

New radius = $3r$ 

Therefore, the curved surface area = $2\pi  \times 3r \times h'$ 

$ = 6\pi rh'$

But it is mentioned in the question that the curved surface area is unchanged. Therefore, we get

$ \Rightarrow 6\pi rh' = 2\pi rh$

$ \Rightarrow 6h' = 2h$

Divide both sides by $6$ 

$ \Rightarrow h' = \dfrac{2}{6}h$

$ \Rightarrow h' = \dfrac{1}{3}h$

13. How many small cubes with an edge of $20cm$ each can be just accommodated in a cubical box of $2m$ edge?

a) $10$

b) $100$

c) $1000$

d) $10000$

Ans: The correct answer is option (c) $1000$ 

We know that volume of a cube with side $a$ = ${a^3}$ 

The volume of a cubical box with edge $2m$ = $8{m^3}$ 

The volume of each small cube with edge $20cm$ = $8000c{m^3}$ 

$ = 0.008{m^3}$ 

Thus, number of small cubes that can be accommodated in the cubical box = Volume of the cubical box $ \div $ volume of small cube

$ = \dfrac{8}{{0.008}}$ 

$ = 1000$ 

14. The volume of a cylinder whose radius $r$ is equal to its height is 

a) $\dfrac{1}{4}\pi {r^3}$

b) $\dfrac{{\pi {r^3}}}{{32}}$

c) $\pi {r^3}$

d) $\dfrac{{{r^3}}}{8}$

Ans: The correct answer is option (c) $\pi {r^3}$

We know that volume of cylinder = $\pi {r^2}h$ 

Here, we are given that $h = r$. Therefore, we get

$ = \pi {r^2}.r$ 

$ = \pi {r^3}$

15. The volume of a cube whose edge is $3x$ is

a) $27{x^3}$

b) $9{x^3}$

c) $6{x^3}$

d) $3{x^3}$

Ans: The correct answer is option (a) $27{x^3}$

We know that volume of a cube with side $a$ = ${a^3}$ 

Therefore, the volume of a cube with side $3x$ = ${\left( {3x} \right)^3}$ 

$ = 27{x^3}$ 

16. The figure ABCD is a quadrilateral in which AB = CD and BC = AD. Its area is 

a) $72c{m^2}$

b) $36c{m^2}$

c) $24c{m^2}$

d) $18c{m^2}$

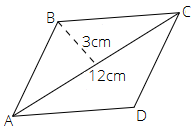
Ans: The correct answer is option (b) $36c{m^2}$

The given quadrilateral ABCD is a parallelogram and the diagonal of the parallelogram divides it into two triangles of equal areas.

Area of $\vartriangle ABC$ = $\dfrac{1}{2} \times base \times height$ 

$ \Rightarrow \dfrac{1}{2} \times 12 \times 3 = 18c{m^2}$

Therefore, are parallelogram = $2 \times area{\text{ }}of{\text{ }}\vartriangle ABC$  \[\Rightarrow 2 \times 18{cm}^{2} = 36{cm}^{2} \]

17. What is the area of a rhombus ABCD below if $AC = 6cm$, and $BE = 4cm$ ?

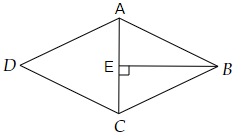
a) $36c{m^2}$

b) $16c{m^2}$

c) $24c{m^2}$

d) $13c{m^2}$

Ans: The correct answer is option (c) $24c{m^2}$

We can see in the given figure that the diagonal AC of the rhombus ABCD divides the rhombus into two triangles of equal areas.

Area of $\vartriangle ABC$ = $\dfrac{1}{2} \times base \times height$ 

$ \Rightarrow \dfrac{1}{2} \times 4 \times 6 = 12c{m^2}$

Therefore, are of rhombus = $2 \times area{\text{ }}of{\text{ }}\vartriangle ABC$ 

$ \Rightarrow 2 \times 12c{m^2} = 24c{m^2}$ 

18. The area of a parallelogram is $60c{m^2}$ and one of its altitudes is $5cm$. The length of its corresponding side is 

a) $12cm$

b) $6cm$

c) $4cm$

d) $2cm$

Ans: The correct answer is option (a) $12cm$

We know that area of parallelogram = sides $ \times $ altitude. Therefore, on substituting the values, we get

$ \Rightarrow 60 = side \times 5$ 

$ \Rightarrow side \times 5 = 60$

Divide both sides by $5$ 

$ \Rightarrow side = 12cm$

19. The perimeter of a trapezium is $52cm$ and its each non-parallel side is equal to $10cm$ with its height $8cm$. Its area is

a) $124c{m^2}$

b) $118c{m^2}$

c) $128c{m^2}$

d) $112c{m^2}$

Ans: The correct answer is option (c) $128c{m^2}$

Given that, the perimeter of a trapezium = $52cm$

And, its each non-parallel side is equal to $10cm$.

Therefore, the sum of its parallel sides = $52 - \left( {10 + 10} \right)$ 

$ = 52 - 20$ 

$ = 32cm$

We know that area of trapezium = $\dfrac{1}{2}\left( {a + b} \right) \times h$. Therefore, we get

$= \dfrac{1}{2} \times 32 \times 8$

$ \Rightarrow 128c{m^2}$

20. Area of a quadrilateral ABCD is $20c{m^2}$ and perpendiculars on BD from opposite vertices are $1cm$ and $1.5cm$. The length of BD is 

a) $4cm$

b) $15cm$

c) $16cm$

d) $182cm$

Ans: The correct answer is option (c) $16cm$

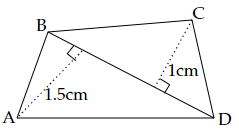
We know that the area of quadrilateral = $\dfrac{1}{2}\left( \text{sum of altitudes} \right) \times \text{corresponding diagonal}$. Therefore, we get

$ \Rightarrow 20 = \dfrac{1}{2}\left( {1 + 1.5} \right) \times BD$ 

$ \Rightarrow 20 \times 2 = 2.5 \times BD$

$ \Rightarrow 2.5 \times BD = 40$

$ \Rightarrow BD = \dfrac{{40}}{{2.5}}$

$ \Rightarrow BD = 16cm$

21. A metal sheet $27cm$ long, $8cm$ broad and $1cm$ thick is melted into a cube. The side of the cube is 

a) $6cm$

b) $8cm$

c) $12cm$

d) $24cm$

Ans:  The correct answer is option (a) $6cm$

Given, a metal sheet is $27cm$ long, $8cm$ broad and $1cm$

Therefore, the volume of the metal sheet = \[27cm \times 8cm \times 1cm\] 

$ = 216c{m^3}$ 

It is given in the question that the sheet was melted to form a cube. Therefore, the volume of the metal sheet = the volume of the cube.

Thus, the volume of cube = $216c{m^3}$

We know that volume of a cube with side $n$ = ${n^3}$ 

Let the length of the side of the given cube be $a$.

$ \Rightarrow {a^3} = 216c{m^3}$

Take cube root on both the sides,

$ \Rightarrow a = 6cm$

22. Three cubes of metal whose edges are $6cm$, $8cm$ and $10cm$ respectively are melted to form a single cube. The edge of the new cube is

a) $12cm$

b) $24cm$

c) $18cm$

d) $20cm$

Ans: The correct answer is option (a) $12cm$

The edges of cubes are $6cm$, $8cm$ and $10cm$

We know that volume of a cube with side $a$ = ${a^3}$ 

Therefore, the sum of the volumes of three metal cubes = ${6^3} + {8^3} + {10^3}$ 

$ \Rightarrow 216 + 512 + 1000 = 1728c{m^3}$ 

Thus, the volume of new cube $1728c{m^3}$

Let the side of the new cube be $a$. Therefore,

$ \Rightarrow {a^3} = 1728c{m^3}$

Take cube root on both the sides,

$ \Rightarrow a = 12cm$

23. A covered wooden box has the inner measures as $115cm$, $75cm$ and $35cm$ and thickness of wood as $2.5cm$. The volume of the wood is

a) $85,000c{m^3}$

b) $80,000c{m^3}$

c) $82,125c{m^3}$

d) $84,000c{m^3}$

Ans: The correct answer is option (c) $82,125c{m^3}$

Given, the inner measure of the wooden box as $115cm$, $75cm$ and $35cm$.

The thickness of the box is $2.5cm$. Therefore,

The outer measurements of wooden box will be $\left( {115 + 5} \right)cm$, $\left( {75 + 5} \right)cm$ and $\left( {35 + 5} \right)cm$ i.e. $120cm$, $80cm$ and $40cm$.

We know that the volume of the cube = $l \times b \times h$. Therefore, we get

The volume of outer box = $120 \times 80 \times 40c{m^3}$ 

$ = 384000c{m^3}$ 

The volume of the inner box = $115 \times 75 \times 35c{m^3}$ 

$ = 301875c{m^3}$ 

Thus, the volume of wood = outer volume $ - $ inner volume

$ \Rightarrow 384000c{m^3} - 301875c{m^3}$

$ = 82125c{m^3}$

24. The ratio of radii of two cylinders is $1:2$ and heights are in the ratio $2:3$. The ratio of their volumes is 

a) $1:6$

b) $1:9$

c) $1:3$

d) $2:9$

Ans: The correct answer is option (a) $1:6$

Let the radii of two cylinders be ${r_1}$ and ${r_2}$.

Ans, the heights of two cylinders be ${h_1}$ and ${h_2}$.

Therefore, $\dfrac{{{r_1}}}{{{r_2}}} = \dfrac{1}{2}$ and $\dfrac{{{h_1}}}{{{h_2}}} = \dfrac{2}{3}$

We know that the volume of the cylinder = $\pi {r^2}h$. Therefore, we get

$ \Rightarrow \dfrac{{{v_1}}}{{{v_2}}} = \dfrac{{\pi r_1^2{h_1}}}{{\pi r_2^2{h_2}}}$ 

On substituting the values, we get

$ \Rightarrow \dfrac{{{v_1}}}{{{v_2}}} = {\left( {\dfrac{1}{2}} \right)^2}\dfrac{2}{3}$

$ \Rightarrow \dfrac{{{v_1}}}{{{v_2}}} = \dfrac{1}{4} \times \dfrac{2}{3}$

$ \Rightarrow \dfrac{{{v_1}}}{{{v_2}}} = \dfrac{1}{6}$

Hence, ${v_1}:{v_2} = 1:6$ 

25. Two cubes have volumes in the ratio $1:64$. The ratio of the area of a face of first cube to that of the other is 

a) $1:4$

b) $1:8$

c) $1:16$

d) $1:32$ 

Ans: The correct answer is option (c) $1:16$

Let the edges to the two cubes be $a$ and $b$.

We know that volume of a cube with side $n$ = ${n^3}$ 

Therefore, according to the question

$ \Rightarrow {a^3}:{b^3} = 1:64$ 

$ \Rightarrow \dfrac{{{a^3}}}{{{b^3}}} = {\left( {\dfrac{1}{4}} \right)^3}$

Take cube root on both sides.

$ \Rightarrow \dfrac{a}{b} = \dfrac{1}{4}$

We know that the surface area of the cube with side $n$ = $6{n^2}$ 

Therefore, the ratio of areas = ${\left( {\dfrac{a}{b}} \right)^2} = {\left( {\dfrac{1}{4}} \right)^2}$

$ \Rightarrow \dfrac{{{a^2}}}{{{b^2}}} = \dfrac{1}{{16}}$

Therefore, ${a^2}:{b^2} = 1:16$ 

26. The surface areas of the six faces of a rectangular solid are $16$, $16$, $32$, $32$, $72$ and $72$ square centimeters. The volume of the solid, in cubic centimeters, is 

a) $192$

b) $384$

c) $480$

d) $2592$ 

Ans: The correct answer is option (a) $192$

Since, the solid has rectangular faces, with length $l$, breadth $b$ and height $h$ 

Therefore, we have,

$ \Rightarrow l \times b = 16.......\left( i \right)$ 

$ \Rightarrow b \times h = 32.......\left( {ii} \right)$

$ \Rightarrow l \times h = 72.......\left( {iii} \right)$

On multiplying equations $\left( i \right)$, $\left( {ii} \right)$ and $\left( {iii} \right)$, we get

$ \Rightarrow l \times l \times b \times b \times h \times h = 16 \times 32 \times 72$ 

$ \Rightarrow {l^2} \times {b^2} \times {h^2} = 16 \times 32 \times 72$

$ \Rightarrow {l^2}{b^2}{h^2} = 36864$

Take square root on both the sides,

$ \Rightarrow lbh = 192$

27. Ramesh has three containers. 

a) Cylindrical container A having radius $r$ and height $h$, 

b) Cylindrical container B having radius $2r$ and height $\dfrac{1}{2}h$, and 

c) Cuboidal container C having dimensions $r \times r \times h$ 

The arrangement of the containers in the increasing order of their volumes is 

a) A, B, C

b) B, C, A

c) C, A, B

d) Cannot be arranged

Ans: The correct answer is option (c) C, A, B

We know that volume of a cylinder having radius $r$ and $h$ = $\pi {r^2}h$. Therefore, 

a) The volume of cylindrical container A having radius $r$ and height $h$ = $\pi {r^2}h$ 

b) The volume of cylindrical container B having radius $2r$ and height $\dfrac{1}{2}h$ = $\pi {\left( {2r} \right)^2} \times \dfrac{1}{2}h$ 

$ = \pi  \times 4{r^2} \times \dfrac{1}{2}h$

$ = 2\pi {r^2}h$

c) We know that volume of cuboid = $l \times b \times h$. Therefore,

The volume of cuboidal container C having dimensions $r \times r \times h$ = ${r^2}h$ 

So, we can figure out from (a), (b) and (c) that we have the following order C, A, B

28. If $R$ is the radius of the base of the hat, then the total outer surface area of the hat is 

a) $\pi r\left( {2h + R} \right)$

b) $2\pi r\left( {h + R} \right)$

c) $2\pi rh + \pi {R^2}$

d) None of these

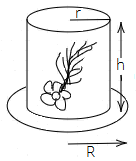
Ans: The correct answer is option (c) $2\pi rh + \pi {R^2}$

We have, cylinder hat with base radius $R$ and radius of the top surface = $r$ 

The total surface area of the hat = curved surface area + top surface area + base surface area.

We know that the curved surface area of the cylinder = $2\pi rh$. Therefore,

The curved surface area of hat = $2\pi rh$

We know that area of circle = $\pi {r^2}$. Therefore, 

The top surface area of the hat = $\pi {r^2}$

The surface area of base = $\pi \left( {{R^2} - {r^2}} \right)$ 

On addition, we get

The total surface area of the hat = $2\pi rh + \pi {r^2} + \pi \left( {{R^2} - {r^2}} \right)$ 

$= 2\pi rh + \pi {r^2} + \pi {R^2} - \pi {r^2}$

$= 2\pi rh + \pi {R^2}$

Thus, the total outer surface area of the hat is $2\pi rh + \pi {R^2}$

In the questions $29$ to $52$, fill in the blanks to make the statements true.

29. A cube of side $4cm$ is painted on all its sides. If it is sliced in $1$ cubic cm cubes, then the number of such cubes that will have exactly two of their faces painted is ______.

Ans: The value of filler is $24$.

Given, side of the cube = $4cm$ 

Thus, the volume of the a cube = ${4^3}$ = $64c{m^3}$ 

So, on slicing the cube of side $4cm$, $64$ small cubes will be obtained.

On each side of the larger cube, the smaller cubes in the edges will have more than one face painted.

The cubes which are situated at the corners of the larger cube have three painted faces. 

So, to each edge, two small cubes are left which have two painted faces. As the total number of edges in a cube are $12$.

Thus, the no. of small cubes with two painted faces = $12 \times 2$ = $24$.

30. A cube of side $5cm$ is cut into $1$ cm cubes. The percentage increase in volume after such cutting is _______. 

Ans: The answer of filler is none.

Given that, a cube of side $5cm$ is cut into $1$ cm cubes.

The volume of larger cube = ${5^3}$ = $125c{m^3}$ 

The volume of small cube = ${1^3}$ = $1c{m^3}$ 

Now, the larger cube is cut into $1cm$ cubes.

Thus, the number of small cubes = $\dfrac{{125}}{{Vol.{\text{ }}of{\text{ }}1{\text{ }}small{\text{ }}cube}}$ = $\dfrac{{125}}{1}$ 

So, the volume of $125$ cubes of side $1cm$ = $125c{m^3}$ 

Hence, there is no change in the volume.

31. The surface area of a cuboid formed by joining two cubes of side $a$ face to face is _________.

Ans: The value of filler is $10{a^2}$ 

Two cubes of side $a$ are joined face to face and form a cuboid that has the same height and breadth as the cube. But joined cubes or the cuboid formed has the length twice the length of a cube. Therefore, we have

$ \Rightarrow l = 2a$, $b = a$ and $h = a$ 

We know that the total surface of a cuboid = $2\left( {lb + bh + hl} \right)$. Therefore, on substituting the values, we get

$= 2\left( {2a \times a + a \times a + a \times 2a} \right)$

$= 2\left( {2{a^2} + {a^2} + 2{a^2}} \right)$

$= 2\left( {5{a^2}} \right)$

$= 10{a^2}$

32. If the diagonals of a rhombus get doubled, then the area of the rhombus becomes __________ its original area. 

Ans: The answer of filler is $4$ times

We know that area of the rhombus having diagonal ${d_1}$ and ${d_2}$ = $\dfrac{1}{2} \times {d_1} \times {d_2}$ 

If the diagonals are doubled, the new area = $\dfrac{1}{2} \times 2{d_1} \times 2{d_2}$ = $4\left( {\dfrac{1}{2} \times {d_1} \times {d_2}} \right)$

Thus, the new area is $4$ times the original area.

33. If a cube fits exactly in a cylinder with height $h$, then the volume of the cube is __________ and surface area of the cube is __________. 

Ans: The values of fillers are ${h^3}$, $6{h^2}$. 

Since the cube fits exactly in the cylinder with height $h$, therefore each side of a cube is $h$

Thus, the volume of the cube having side $h$ = ${h^3}$ 

Surface area of the cube having side $h$ = $6{h^2}$.

34. The volume of a cylinder becomes __________ the original volume if its radius becomes half of the original radius. 

Ans: The value of filler is $\dfrac{1}{4}$ 

We know that volume of a cylinder having radius $r$ and height $h$ = $\pi {r^2}h$ 

If the radius is halved, the new volume = $\pi {\left( {\dfrac{r}{2}} \right)^2}h$ = $\dfrac{1}{4}\pi {r^2}h$

Thus, the new volume is $\dfrac{1}{4}$ of the original volume.

35. The curved surface area of a cylinder is reduced by ____________ percent if the height is half of the original height. 

Ans: The value of filler is $50\% $ 

We know that the curved surface area of a cylinder having radius $r$ and height $h$ = $2\pi rh$ 

If the height is halved, new curved surface area = $2\pi r \times \dfrac{h}{2}$ = $\dfrac{1}{2}\left( {2\pi rh} \right)$

Thus, the new curved surface area is reduced by $50\% $.

36. The volume of a cylinder which exactly fits in a cube of side $a$ is _______. 

Ans: The value of filler is $\dfrac{{\pi {a^3}}}{4}$ 

The cylinder that exactly fits in a cube of side $a$ has its height equal to the edge of the cube and radius is equal to half the edge of the cube.

Therefore, height = $a$, radius = $\dfrac{a}{2}$ 

We know that volume of a cylinder having radius $r$ and height $h$ = $\pi {r^2}h$ 

Therefore, the volume of the a cylinder having height $a$ and radius $\dfrac{a}{2}$ = $\pi {\left( {\dfrac{a}{2}} \right)^2} \times a$

$ = \dfrac{1}{4}\pi {a^3}$ 

37. The surface area of a cylinder which exactly fits in a cube of side $b$ is _______.

Ans: The value of filler is $\pi {b^2}$ 

The cylinder that exactly fits in a cube of side $b$ has its height equal to the edge of the cube and radius is equal to half the edge of the cube.

Therefore, height = $b$, radius = $\dfrac{b}{2}$ 

We know that the curved surface area of cylinder having radius $r$ and height $h$ = $2\pi rh$ 

Therefore, the curved surface area of a cylinder having height $b$ and radius $\dfrac{b}{2}$ = $2\pi  \times \dfrac{b}{2} \times b$

$ = \pi {b^2}$ 

38. If the diagonal $d$ of a quadrilateral is doubled and the heights ${h_1}$ and ${h_2}$ falling on $d$ are halved, then the area of the quadrilateral is ________. 

Ans: The value of filler is $\dfrac{1}{2}\left( {{h_1} + {h_2}} \right)d$ 

Assume that PQRS be a quadrilateral, ${h_1}$ and ${h_2}$ are the heights on the diagonal QS = $d$, then, area of quadrilateral = $\dfrac{1}{2}\left( {{h_1} + {h_2}} \right)d$ 

In the given case, the diagonal is doubled and heights are halved. Therefore, the area of the quadrilateral becomes $\dfrac{1}{2}\left( {\dfrac{{{h_1}}}{2} + \dfrac{{{h_2}}}{2}} \right)2d$

$ = \dfrac{1}{2}\left( {\dfrac{{{h_1} + {h_2}}}{2}} \right)2d$

$ = \dfrac{1}{2}\left( {{h_1} + {h_2}} \right)d$

39. The perimeter of a rectangle becomes ________ times its original perimeter, if its length and breadth are doubled. 

Ans: The value of filler is $2$ 

The perimeter of a rectangle having length $l$ and breadth $b$ = $2\left( {l + b} \right)$ 

If the length and breadth are doubled, the new perimeter = $2\left( {2l + 2b} \right)$

$ = 2\left[ {2\left( {l + b} \right)} \right]$ 

40. A trapezium with $3$ equal sides and one side double the equal side can be divided into ________ equilateral triangles of _______ area. 

Ans: The answer of fillers are $3$, equal.

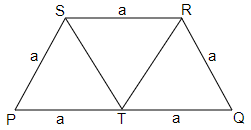
Let PQRS is a trapezium in which 

PS = SR = QR = $a$ and PQ = $2a$ 

Now, we will draw medians through the vertices S and R on the side PQ.

PT = TQ = $a$ 

Now, in parallelogram PSRT, we have

PS = TR = $a$ and PT = RS = $a$ (parallelogram has equal opposite sides)

In triangle PST and STR,

PS = TR, PT = RS, ST = QR.

Thus, the triangles PST and STR are equilateral triangles having equal sides.

Hence, trapezium can be divided into $3$ equilateral triangles of equal area.

41. All six faces of a cuboid are __________ in shape and of ______ area. 

Ans: Rectangular, different

42. Opposite faces of a cuboid are _________ in area. 

Ans: Equal

43. Curved surface area of a cylinder of radius $h$ and height $r$ is _______. 

Ans: $2\pi hr$ 

44. Total surface area of a cylinder of radius $h$ and height $r$ is _________.

Ans: The answer of filler is $2\pi h\left( {r + h} \right)$ 

Given that, radius = $h$ and height = $r$ 

Total surface area of a cylinder = curved surface area + area of top surface + area of the base surface.

The total surface area of a cylinder = $2\pi hr + \pi {h^2} + \pi {h^2}$ 

$ = 2\pi rh + 2\pi {h^2}$

$ = 2\pi h\left( {r + h} \right)$

45. Volume of a cylinder with radius $h$ and height $r$ is __________.

Ans: $\pi {h^2}r$ 

46. Area of a rhombus = $\dfrac{1}{2}$ product of _________. 

Ans: Diagonals

47. Two cylinders A and B are formed by folding a rectangular sheet of dimensions $20cm \times 10m$ along its length and also along its breadth respectively. Then volume of A is ________ of volume of B. 

Ans: The answer of filler is twice.

Given, rectangular sheet of dimension $20cm \times 10m$

Case 1: If we fold a sheet along its length, which is $20cm$, then the figure obtained is a cylinder with height $10cm$ and base circumference $2\pi r = 20cm$

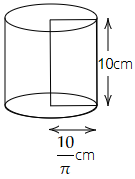
Here, $r = \dfrac{{10}}{\pi }cm$ 

Therefore, the volume of the cylinder $\left( v \right)$  = $\pi {r^2}h$ 

$ \Rightarrow v = \pi  \times \dfrac{{10}}{\pi } \times \dfrac{{10}}{\pi } \times 10$ 

$ \Rightarrow v = \dfrac{{1000}}{\pi }c{m^3}$ 

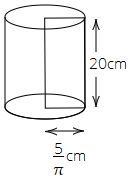
Case 2: If we fold the rectangular sheet along its breadth, which is $10cm$, then the resultant figure is a cylinder with height $h$ and base circumference = $2\pi r$ = $10cm$.

Here, $r = \dfrac{{10}}{{2\pi }} = \dfrac{5}{\pi }cm$

Therefore, the volume of the cylinder $\left( V \right)$  = $\pi {r^2}h$ 

$ \Rightarrow V = \pi  \times \dfrac{5}{\pi } \times \dfrac{5}{\pi } \times 20$

$ \Rightarrow V = \dfrac{{500}}{\pi }c{m^3}$

Therefore, we get $V = 2v$.

Hence, the volume of A is twice the volume of B.

48. In the above question, the curved surface area of A is ________ curved surface area of B.

Ans: Same as 

We know that the curved surface area of cylinder = $2\pi rh$ 

For cylinder A, we have $h = 10cm$ and radius = $\dfrac{{10}}{\pi }cm$ 

Therefore, curved surface area of cylinder A = $2\pi  \times \dfrac{{10}}{\pi } \times 10$

$ = 200c{m^2}$ 

For cylinder B, we have $h = 20cm$ and radius = $\dfrac{5}{\pi }cm$ 

Therefore, the curved surface area of cylinder B = $2\pi  \times \dfrac{5}{\pi } \times 20$

$ = 200c{m^2}$ 

Hence, the curved surface area of both cylinders is the same.

49. __________ of a solid is the measurement of the space occupied by it. 

Ans: Volume

50. __________ surface area of room = area of $4$ walls. 

Ans: Lateral

51. Two cylinders of equal volume have heights in the ratio $1:9$. The ratio of their radii is ________. 

Ans: The value of filler is $3:1$

Let the radii be ${r_1}$, ${r_2}$ and heights of two cylinders be ${h_1}$ and ${h_2}$ 

The heights of the cylinders are given as, $\dfrac{{{h_1}}}{{{h_2}}} = \dfrac{1}{9}$.

We know that volume of cylinder = $\pi {r^2}h$ 

According to the question,

$ \Rightarrow \pi r_1^2{h_1} = \pi r_2^2{h_2}$

$ \Rightarrow \dfrac{{r_1^2}}{{r_2^2}} = \dfrac{{{h_2}}}{{{h_1}}}$

$ \Rightarrow \dfrac{{r_1^2}}{{r_2^2}} = \dfrac{9}{1}$

Take root on both the sides

$ \Rightarrow \dfrac{{{r_1}}}{{{r_2}}} = \dfrac{3}{1}$

$ \Rightarrow {r_1}:{r_2} = 3:1$

52. Two cylinders of the same volume have their radii in the ratio $1:6$ , then the ratio of their heights is ________. 

Ans: The value of filler is $36:1$

Let the radii be ${r_1}$, ${r_2}$ and heights of two cylinders be ${h_1}$ and ${h_2}$ 

Given that, $\dfrac{{{r_1}}}{{{r_2}}} = \dfrac{1}{6}$

We know that volume of cylinder = $\pi {r^2}h$ 

According to the question,

$ \Rightarrow \pi r_1^2{h_1} = \pi r_2^2{h_2}$

$ \Rightarrow \dfrac{{r_1^2}}{{r_2^2}} = \dfrac{{{h_2}}}{{{h_1}}}$

$ \Rightarrow {\left( {\dfrac{1}{6}} \right)^2} = \dfrac{{{h_2}}}{{{h_1}}}$

\[ \Rightarrow \dfrac{{{h_2}}}{{{h_1}}} = \dfrac{1}{{36}}\]

\[ \Rightarrow \dfrac{{{h_1}}}{{{h_2}}} = \dfrac{{36}}{1}\]

$ \Rightarrow {h_1}:{h_2} = 36:1$

In question $53$ to $61$, state whether the statements are true (T) or false (F). 

53. The areas of any two faces of a cube are equal. 

Ans: The given statement is true.

Let the length of the side of a cube be $a$

We know that all the faces of a cube are squares of the same side length.

So, area of one face = $a \times a$ = ${a^2}$ 

Area of another face = $a \times a$ = ${a^2}$ 

Hence, areas of any two faces of a cube are equal.

54. The areas of any two faces of a cuboid are equal. 

Ans: The given statement is false.

A cuboid has a rectangular face with different lengths and widths. Only opposite faces of cuboids have the same lengths and widths. Hence, areas of only opposite faces of a cuboid are equal.

55. The surface area of a cuboid formed by joining face to face $3$ cubes of side $x$ is $3$ times the surface area of a cube of side $x$. 

Ans: The given statement is false.

If we join three cubes face-to-face having side $x$, then we will obtain a cuboid. The cuboid formed will have the same height and breadth as the cubes but its length will be thrice that of the cubes.

Hence, the length, breadth and height of the cuboid so formed are $3x$, $x$ and $x$. 

Thus, its surface area = $2\left( {lb + bh + hl} \right)$ 

$ = 2\left( {3x \times x + x \times x + x \times 3x} \right)$

$ = 2\left( {3{x^2} + {x^2} + 3{x^2}} \right)$

$ = 2\left( {7{x^2}} \right)$

$ = 14{x^2}$

The surface area of a cube with side $x$ = $6{x^2}$ 

56. Two cuboids with equal volumes will always have equal surface areas. 

Ans: The given statement is false.

We discard the statement by a counter example.

Let the dimensions of two cuboids be $2cm \times 3cm \times 2cm$ and $2cm \times 1cm \times 6cm$ 

Volume of first cuboid = $l \times b \times h$ = $2cm \times 3cm \times 2cm$ = $12c{m^3}$ 

Volume of second cuboid = $l \times b \times h$ = $2cm \times 1cm \times 6cm$ = $12c{m^3}$ 

Now, let us find the surface area of cuboids.

Surface area of first cuboid = $2\left( {lb + bh + hl} \right)$ = \[2\left( {2cm \times 3cm + 3cm \times 2cm + 2cm \times 2cm} \right)\]

\[ = 2\left( {6c{m^2} + 6c{m^2} + 4c{m^2}} \right)\]

\[ = 2\left( {16c{m^2}} \right)\]

\[ = 32c{m^2}\]

Surface area of second cuboid = $2\left( {lb + bh + hl} \right)$ = \[2\left( {2cm \times 1cm + 1cm \times 6cm + 6cm \times 2cm} \right)\]

\[ = 2\left( {2c{m^2} + 6c{m^2} + 12c{m^2}} \right)\]

\[ = 2\left( {20c{m^2}} \right)\]

\[ = 40c{m^2}\]

The volume of the two cuboids is equal but their surface areas are not equal.

57. The area of a trapezium become $4$ times if its height gets doubled. 

Ans: The given statement is false.

We know that area of a trapezium having sides $a$ and $b$ and height $h$ = $\dfrac{1}{2}\left( {a + b} \right) \times h$ 

If height gets doubled, then the area becomes $\dfrac{1}{2}\left( {a + b} \right) \times 2h$

$ = 2\left( {\dfrac{1}{2}\left( {a + b} \right) \times h} \right)$

Thus, the area is doubled.

58. A cube of side $3cm$ painted on all its faces, when sliced into $1$ cubic centimeter cubes, will have exactly $1$ cube with none of its faces painted. 

Ans: The given statement is true.

Given that, a cube of side $3cm$ is painted on all its faces and this cube is sliced into \[1\] cubic centimeter cubes. Then, there will be $8$ corner cubes that have $3$ sides painted, $6$ center cubes with only one side painted and only $1$ cube in the middle that has no side painted.

59. Two cylinders with equal volume will always have equal surface areas. 

Ans: The given statement is false.

Let us consider two cylinders with the following measures-

Let ${r_1} = 2cm$, ${h_1} = 9cm$ and ${r_2} = 3cm$, ${h_2} = 4cm$ 

We know that volume of cylinder = $\pi {r^2}h$.

For first cylinder,

Volume = $\pi  \times {2^2} \times 9$ = $36\pi c{m^3}$ 

For second cylinder,

Volume = $\pi  \times {3^2} \times 4$ = $36\pi c{m^3}$ 

Thus, volumes are equal.

Now, we will find surface areas. 

We know that the surface area of the cylinder = $2\pi rh$.

For first cylinder,

Surface area = $2\pi  \times 2 \times 9$ = $36\pi c{m^3}$ 

For second cylinder,

Surface area = $2\pi  \times 3 \times 4$ = $24\pi c{m^3}$ 

Thus the given statement is false.

60. The surface area of a cube formed by cutting a cuboid of dimensions $2 \times 1 \times 1$ in $2$ equal parts is $2sq.{\text{ }}units$.

Ans: The given statement is false.

Given that, dimensions of cuboid = $2 \times 1 \times 1$

It is sliced into two equal parts, which are cubes.

Thus, dimensions of the cube so formed = $1 \times 1 \times 1$

Surface area of a cube so formed = $6{\left( a \right)^2}$ 

$ = 6{\left( 1 \right)^2}$

$ = 6sq.{\text{ }}units$

61. Ratio of area of a circle to the area of a square whose side equals radius of circle is $1:\pi $.

Ans: The given statement is false.

Given, side of a circle = radius of a circle.

Let the side of the square and radius of the circle be $r$ 

Thus, area of square = ${r^2}$ 

And the area of the circle = $\pi {r^2}$ 

Now, the ratio of the area of the circle to area of the square = $\pi {r^2}:{r^2}$

$ = \pi :1$

Solve the following.

62. The area of a rectangular field is $48{m^2}$ and one of its sides is $6m$. How long will a lady take to cross the field diagonally at the rate of $20m/\min ute$ ? 

Ans: Given, area of rectangular field = $48{m^2}$ 

One side of the rectangle = $6m$

We know that area of rectangle = $l \times b$. Therefore, we get

$ \Rightarrow 48 = 6 \times b$

$ \Rightarrow b = \dfrac{{48}}{6}$

$ \Rightarrow b = 8m$

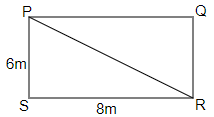
In triangle PRS, $\angle S = 90^\circ $ 

Using Pythagoras theorem, we have

$ \Rightarrow {\left( {PR} \right)^2} = {\left( {PS} \right)^2} + {\left( {SR} \right)^2}$ 

$ \Rightarrow {\left( {PR} \right)^2} = {\left( 6 \right)^2} + {\left( 8 \right)^2}$

$ \Rightarrow {\left( {PR} \right)^2} = 36 + 64$

$ \Rightarrow {\left( {PR} \right)^2} = 100$

$ \Rightarrow PR = 10$

Time taken at rate of $20m/\min $ = \[\dfrac{{\text{distance}}}{{{\text{Speed}}}\]

$ = \dfrac{{10}}{{20}}\min $ 

$ = \dfrac{1}{2}\min $

$ = 30\sec $ 

63. The circumference of the front wheel of a cart is $3m$ long and that of the back wheel is $4m$ long. What is the distance traveled by the cart, when the front wheel makes five more revolutions than the rear wheel? 

Ans: Given that, the circumference of the front wheel of a cart is $3m$

Let $x$ meters be the total distance traveled by the cart.

Number of revolutions = $\dfrac{\text{Distance traveled}}{\text{Circumference}}$ 

Number of revolutions made by front wheel = $\dfrac{x}{3}$ 

Number of revolutions made by rear wheel = $\dfrac{x}{4}$ 

Hence, $\dfrac{x}{3} - \dfrac{x}{4} = 5$

$ \Rightarrow \dfrac{{4x - 3x}}{{12}} = 5$

$ \Rightarrow \dfrac{x}{{12}} = 5$

$ \Rightarrow x = 5 \times 12$

$ \Rightarrow x = 60$

Hence, the distance covered by the cart is $60m$.

64. Four horses are tethered with equal ropes at $4$ corners of a square field of side $70$ meters so that they just can reach one another. Find the area left ungrazed by the horses. 

Ans: Given that, side of square field = $70m$ 

Also, $4$ horses are tethered with equal ropes at $4$ corners of the field. Thus, each horse grazes up to $35m$ of distance along the side.

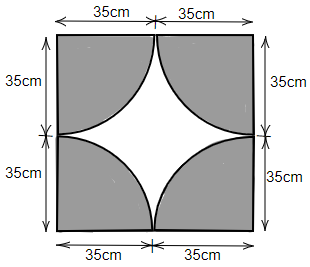
Area of square field = $70 \times 70$ = $4900{m^2}$ 

The grazed area is making a complete circle by taking all the $4$ grazed parts.

Therefore, area of grazed part = $\pi {r^2}$ = $\dfrac{{22}}{7} \times 35 \times 35$ = $3850{m^2}$ 

Ungrazed area left = Area of square field – area of the grazed part

$ = 4900 - 3850$ 

$ = 1050{m^2}$

65. The walls and ceiling of a room are to be plastered. The length, breadth and height of the room are $4.5m$, $3m$, and $350cm$ respectively. Find the cost of plastering at the rate of Rs $8per{\text{ }}{m^2}$.

Ans: We have,

Length of the room $\left( l \right)$ = $4.5m$ 

Breadth of the room $\left( b \right)$ = $3m$

Height of the room $\left( h \right)$ = $3.5m$ 

Thus, area of the walls = $2h\left( {l + b} \right)$ 

$ = 2 \times 3.5 \times \left( {4.5 + 3} \right)$ 

$ = 7 \times 7.5$

$ = 52.5{m^2}$

Area of ceiling = $lb$ = $4.5 \times 3$ = $13.5{m^2}$ 

Area of the room = \[52.5 + 13.5\] = \[66{m^2}\]

Therefore, cost of painting = \[66 \times 8\] = Rs $528$ 

66. Most of the sailboats have two sails, the jib and the mainsail. Assume that the sails are triangles. Find the total area of each sail of the sail boats to the nearest tenth. 

(i). 

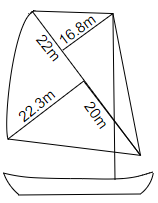
Ans: We know that area of triangle = $\dfrac{1}{2} \times base \times height$ 

In triangle ABC, AC (base) = $22 + 20$ = $42m$ 

BD = height = $22.3m$ 

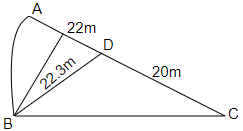
Therefore, area of $\vartriangle ABC$ = $\dfrac{1}{2} \times 42 \times 22.3$ 

$ = \dfrac{{936.6}}{2}$ 

$ = 468.3{m^2}$

In another triangular part,

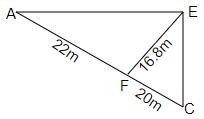
In $\vartriangle ACE$,

EF = height = $16.8m$ 

AC = base = $22 + 20$ = $42m$ 

Thus, area of $\vartriangle ACE$ = $\dfrac{1}{2} \times 42 \times 16.8$

$ = \dfrac{{705.6}}{2}$ 

$ = 352.8{m^2}$

Therefore, area of sailboat (i) = $468.3 + 352.8$ = $821.1{m^2}$ 

(ii). 

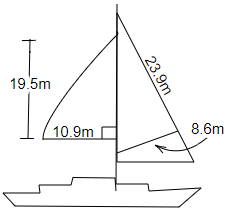
Ans: We know that area of triangle = $\dfrac{1}{2} \times base \times height$ 

In $\vartriangle ABC$, $\angle B = 90^\circ $, $BC = 10.9m$ and height (AB) = $19.5m$ 

Area of $\vartriangle ABC$ = $\dfrac{1}{2} \times 10.9 \times 19.5$ 

$ = \dfrac{{212.55}}{2}$ 

$ = 106.275{m^2}$

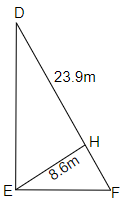
In another triangular part,

Area of $\vartriangle DEF$ = $\dfrac{1}{2} \times DF \times EH$ 

$ = \dfrac{1}{2} \times 23.9 \times 8.6$

$ = \dfrac{{205.54}}{2}$

$ = 102.77{m^2}$

Therefore, area of sailboat (ii) = $106.275 + 102.77$ = $209.045{m^2}$ 

(iii). 

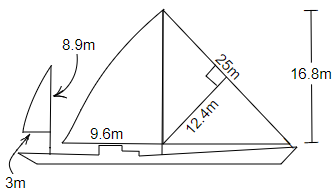
Ans: We know that area of triangle = $\dfrac{1}{2} \times base \times height$ 

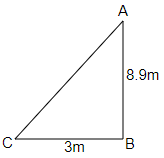
Area of $\vartriangle ABC$ = $\dfrac{1}{2} \times BC \times AB$ 

$ = \dfrac{1}{2} \times 8.9 \times 3$

$ = \dfrac{{26.7}}{2}$

$ = 13.35{m^2}$

In another triangular part,

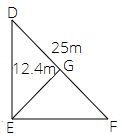
Area of $\vartriangle DEF$ = $\dfrac{1}{2} \times DF \times EG$ 

$ = \dfrac{1}{2} \times 25 \times 12.4$

$ = 155{m^2}$

In another triangular part,

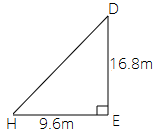
Area of $\vartriangle DEF$ = $\dfrac{1}{2} \times DE \times EH$ 

$ = \dfrac{1}{2} \times 9.6 \times 16.8$

$ = 80.64{m^2}$

Therefore, area of sailboat (iii) = $155 + 80.64$ = $235.64{m^2}$ 

67. The area of a trapezium with equal non-parallel sides is $168{m^2}$. If the lengths of the parallel sides are $36m$ and $20m$, find the length of the non-parallel sides. 

Ans: Given that, the length of the parallel sides is $36m$ and $20m$.

Area of the trapezium = $168{m^2}$

We know that area of trapezium = $\dfrac{1}{2} \times \left( \text{sum of parallel side} \right) \times \text{height}$

Therefore, 

$ \Rightarrow 168 = \dfrac{1}{2}\left( {36 + 20} \right) \times \text{height}$ 

$ \Rightarrow 168 = \dfrac{1}{2} \times 56 \times \text{height}$

$ \Rightarrow 168 = 28 \times \text{height}$

$ \Rightarrow height = \dfrac{{168}}{{28}}$

$ \Rightarrow height = 6m$

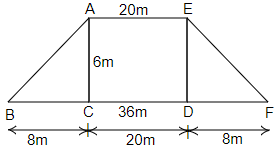
In $\vartriangle ACB$, we have

$ \Rightarrow {\left( {AB} \right)^2} = {\left( {BC} \right)^2} + {\left( {AC} \right)^2}$ 

$ \Rightarrow {\left( {AB} \right)^2} = {\left( 8 \right)^2} + {\left( 6 \right)^2}$

$ \Rightarrow {\left( {AB} \right)^2} = 64 + 36$

$ \Rightarrow {\left( {AB} \right)^2} = 100$

$ \Rightarrow AB = \sqrt {100} $

$ \Rightarrow AB = 10m$

68. Mukesh walks around a circular track of radius $14m$ with a speed of $4km/hr$. If he takes $20$ rounds of the track, for how long does he walk?

Ans: Given that, the radius of circular track = $14m$

Circumference of the circular track = $2\pi r$ = $2 \times \dfrac{{22}}{7} \times 14$ 

$ = 2 \times 22 \times 2$

$ = 88m$

Thus, total distance covered in $20$ rounds = $88 \times 20$ = $1760m$ 

Speed of Mukesh on the circular track = $4km/hr$

$ = \dfrac{{4 \times 1000}}{{60}}$ 

$ = \dfrac{{2 \times 100}}{3}$

$ = \dfrac{{200}}{3}m/\min $

Time taken by Mukesh = $\dfrac{{1760}}{{\dfrac{{200}}{3}}}$ = $\dfrac{{176 \times 3}}{{20}}$ = $26.4\min $ 

$ \Rightarrow 26.4\min  = 26\min {\text{ 24}}sec$ 

69. The areas of two circles are in the ratio $49:64$. Find the ratio of their circumferences. 

Ans: Given that, areas of two circles are in the ratio $49:64$.

We know that area of circle = $\pi {r^2}$ 

Let the area of the first circle be $\pi r_1^2$ and the area of the second circle be $\pi r_2^2$

We have, $\dfrac{{\pi r_1^2}}{{\pi r_2^2}} = \dfrac{{49}}{{64}}$ 

$ \Rightarrow \dfrac{{r_1^2}}{{r_2^2}} = \dfrac{{49}}{{64}}$

$ \Rightarrow \dfrac{{r_1^2}}{{r_2^2}} = \dfrac{{{7^2}}}{{{8^2}}}$

Take square root on both the sides,

$ \Rightarrow \dfrac{{{r_1}}}{{{r_2}}} = \dfrac{7}{8}$

$ \Rightarrow {r_1} = 7$ and ${r_2} = 8$ 

The ratio of circumference of these two circles = $\dfrac{{2\pi {r_1}}}{{2\pi {r_2}}}$ 

$ = \dfrac{{2\pi  \times 7}}{{2\pi  \times 8}}$

$ = \dfrac{7}{8}$

$ = 7:8$

70. There is a circular pond and a footpath runs along its boundary. A person walks around it, exactly once keeping close to the edge. If his step is $66cm$ long and he takes exactly $400$ steps to go around the pond, find the diameter of the pond. 

Ans: Let $r$ be the radius of the pond.

Thus, diameter $\left( d \right)$ of pond = $2r$ 

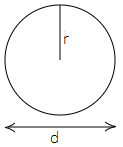
Since a person takes $400$ steps with $66cm$ long each step to go round the pond.

Hence, the circumference of the pond = $66 \times 400$ = $26400cm$ 

$ = \dfrac{{26400}}{{100}}m$ 

$ = 264m$

We know that circumference of circle = $2\pi r$ 

$ \Rightarrow 2\pi r = 264$

$ \Rightarrow r = \dfrac{{264}}{{2\pi }}$

$ \Rightarrow r = 132 \times \dfrac{7}{{22}}$

$ \Rightarrow r = 42m$

Hence, the radius of the pond = $42m$ 

So, the diameter of the pond = $2 \times 42$ = $84m$ 

71. A running track has $2$ semicircular ends of radius $63m$ and two straight lengths. The perimeter of the track is $1000m$. Find each straight length. 

Ans: Given that, the radius of semi-circular track = $63m$

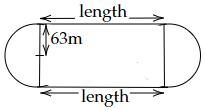
The perimeter of two semi-circles = perimeter of $1$ circle.

The perimeter of the circular track = $2\pi r$. Therefore, on substituting the values, we get

$ = 2 \times \dfrac{{22}}{7} \times 63$ 

$ = 2 \times 22 \times 9$

$ = 396m$

It is given that perimeter of total track = $1000m$

Therefore, length of $2$ straight length tracks = $1000 - 396$ 

$ = 604m$ 

Length, $l$ of one straight length track = $\dfrac{{604}}{2}$ = $302m$ 

72. Find the perimeter of the given figure.

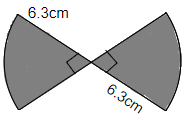
Ans: Radius of the given figure = $6.3m$ 

Two sections in the given figure form a semi-circle.

Perimeter of semi-circle figure = $\dfrac{{2\pi r}}{2} + 2r$ = $\pi r + 2r$ 

$ = \dfrac{{22}}{7} \times 6.3 + 2 \times 6.3$ 

$ = 22 \times 0.9 + 2 \times 6.3$

$ = 19.8 + 12.6$

$ = 32.4m$

73. A bicycle wheel makes $500$ revolutions in moving $1km$. Find the diameter of the wheel. 

Ans: Given that, a bicycle wheel makes $500$ revolutions in moving $1km$.

Therefore, in one revolution, the bicycle wheel covers $\dfrac{1}{{500}}km$ = $\dfrac{{1000}}{{500}}m$ = $2m$ 

Distance of $1$ revolution = circumference of the wheel

$ \Rightarrow 2\pi r = 2$ 

$ \Rightarrow 2 \times \dfrac{{22}}{7} \times r = 2$

$ \Rightarrow r = 2 \times \dfrac{7}{{22}} \times \dfrac{1}{2}$

$ \Rightarrow r = \dfrac{7}{{22}}$

Hence, diameter $\left( d \right)$ = $2r$ = $2 \times \dfrac{7}{{22}}$ = $\dfrac{7}{{11}}$ = $0.636m$ 

74. A boy is cycling such that the wheels of the cycle are making $140$ revolutions per hour. If the diameter of the wheel is $60cm$, calculate the speed in km/h with which the boy is cycling. 

Ans: We have, the diameter of the wheel = $60cm$

Thus, radius = $30cm$

We know that the circumference of the circle = $2\pi r$. Therefore, the circumference of the wheel is

$ = 2 \times \dfrac{{22}}{7} \times 30$ 

$ = \dfrac{{44}}{7} \times 30$

$ = 188.57cm$

Distance covered in $140$ revolutions = $140 \times 188.57$ 

$ = 26400cm$

Therefore, speed = distance/time

$ = \dfrac{{26400}}{{100000}}$ 

$ = 0.264km/h$

75. Find the length of the largest pole that can be placed in a room of dimensions $12m \times 4m \times 3m$ 

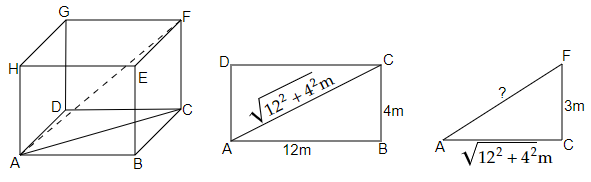
Ans: We have, $\vartriangle ACF$ in which 

$\angle C = 90^\circ $ 

$CF = 3m$ 

$AC = \sqrt {{{\left( {12} \right)}^2} + {{\left( 4 \right)}^2}} $ 

The length of the largest pole = length of diagonal of the cuboid (in the shape of the room)

$ \Rightarrow {\left( {AF} \right)^2} = {\left( {AC} \right)^2} + {\left( {CF} \right)^2}$ 

$ \Rightarrow {\left( {AF} \right)^2} = {\left( {\sqrt {{{\left( {12} \right)}^2} + {{\left( 4 \right)}^2}} } \right)^2} + {\left( 3 \right)^2}$

$ \Rightarrow {\left( {AF} \right)^2} = {\left( {12} \right)^2} + {\left( 4 \right)^2} + {\left( 3 \right)^2}$

$ \Rightarrow {\left( {AF} \right)^2} = 144 + 16 + 9$

$ \Rightarrow AF = \sqrt {144 + 16 + 9} $

$ \Rightarrow AF = \sqrt {169} $

$ \Rightarrow AF = 13m$

Therefore, the length of the largest pole that can be placed in a room of dimensions $12m \times 4m \times 3m$ is $13m$.

Find the area of the following fields. All dimensions are in meters.

76. 

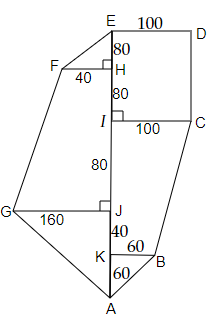
Ans: Area of the given figure = area of $\vartriangle EFH$ + area of rectangle EDCI + area of trapezium FHJG + area of trapezium ICBK + area of $\vartriangle GJA$ + area of $\vartriangle KBA$ 

Let us first find the area of the triangles. We know that area of triangle = $\dfrac{1}{2} \times base \times height$ 

Therefore, area of $\vartriangle EFH$ = $\dfrac{1}{2} \times 40 \times 80$ = $1600{m^2}$ 

Area of $\vartriangle GJA$ = $\dfrac{1}{2} \times 160 \times 100$ = $8000{m^2}$ 

Area of $\vartriangle KBA$ = $\dfrac{1}{2} \times 60 \times 60$ = $1800{m^2}$ 

Let us find the area of the rectangle. We know that area of rectangle = $l \times b$ 

Therefore, 

Area of rectangle EDCI = $100 \times 160$ = $16000{m^2}$ 

Now, let us find the area of trapeziums. We know that area of trapezium = $\dfrac{1}{2} \times \left( \text{sum of parallel side} \right) \times \text{height}$ 

Therefore, the area of trapezium FHJG = $\dfrac{1}{2} \times \left( {40 + 160} \right) \times 160{m^2}$ 

$ = \dfrac{{200}}{2} \times 160{m^2}$

$ = 16000{m^2}$

Therefore, the area of trapezium ICBK = $\dfrac{1}{2} \times \left( {60 + 100} \right) \times 120{m^2}$ 

$ = 80 \times 120{m^2}$

$ = 9600{m^2}$

Thus, the area of complete figure = $1600 + 16000 + 16000 + 9600 + 8000 + 1800$ = $53000{m^2}$ 

77. 

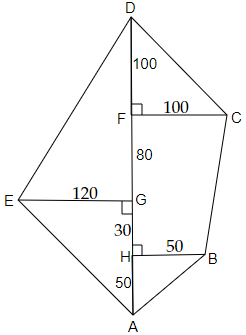
Ans: Area of the given figure = area of $\vartriangle DCF$ + area of $\vartriangle DEG$ + area of trapezium FCBH + area of $\vartriangle EGA$ + area of $\vartriangle AHB$ 

Now, let us find the area of figures one by one.

Area of $\vartriangle DCF$ = $\dfrac{1}{2} \times base \times \text{height}$ = $\dfrac{1}{2} \times 100 \times 100$ = $\dfrac{{10000}}{2}$ = $5000{m^2}$ 

Area of $\vartriangle DEG$ = $\dfrac{1}{2} \times base \times \text{height}$ = $\dfrac{1}{2} \times 120 \times 180$ = $60 \times 180$ = $10800{m^2}$ 

Area of trapezium FCBH = $\dfrac{1}{2} \times \left( \text{sum of parallel side} \right) \times \text{height}$ = $\dfrac{1}{2} \times \left( {100 + 50} \right) \times 110$ = $75 \times 110$ = $8250{m^2}$ 

Area of $\vartriangle EGA$ = $\dfrac{1}{2} \times base \times \text{height}$ = $\dfrac{1}{2} \times 120 \times 80$ = $60 \times 80$ = $4800{m^2}$ 

Area of $\vartriangle AHB$ = $\dfrac{1}{2} \times base \times \text{height}$ = $\dfrac{1}{2} \times 50 \times 50$ = $25 \times 50$ = $1250{m^2}$ 

Thus, the area of the complete figure = $5000 + 10800 + 8250 + 4800 + 1250$ = $30100{m^2}$ 

Find the area of the shaded portion in the following.

78. 

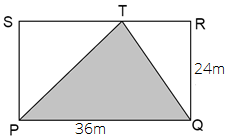
Ans: Here, the shaded region is $\vartriangle PTQ$ 

We know that area of triangle = $\dfrac{1}{2} \times base \times height$ 

In $\vartriangle PTQ$ base is PQ and height = RQ

Therefore, area of $\vartriangle PTQ$ = $\dfrac{1}{2} \times 36 \times 24$ = $18 \times 24$ = $432{m^2}$ 

Thus, the area of the shaded region is $432{m^2}$.

79. 

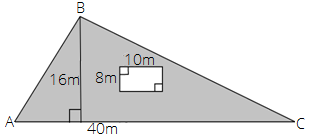
Ans: Area of shaded region = area of $\vartriangle ABC$ - area of the rectangle

We know that area of triangle = $\dfrac{1}{2} \times base \times height$ 

Therefore, area of $\vartriangle ABC$ = $\dfrac{1}{2} \times AC \times BD$ 

$ = \dfrac{1}{2} \times 40 \times 16{m^2}$

$ = 20 \times 16{m^2}$

$ = 320{m^2}$

We know that area of rectangle = $l \times b$ 

$ = 10 \times 8 = 80{m^2}$ 

Thus, area of shaded region = $\left( {320 - 80} \right){m^2}$ = $240{m^2}$ 

80. 

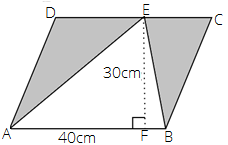
Ans: Area of the shaded region = area of parallelogram ABCD – area of $\vartriangle ABE$ 

We know that area of parallelogram = $side \times height$ 

Therefore, area of parallelogram ABCD = $40 \times 30$ = $1200c{m^2}$ 

We know that area of triangle = $\dfrac{1}{2} \times base \times height$ 

Therefore, area of $\vartriangle ABE$ = $\dfrac{1}{2} \times AB \times EF$ 

$ = \dfrac{1}{2} \times 40 \times 30c{m^2}$

$ = 20 \times 30c{m^2}$

$ = 600c{m^2}$

Thus, area of shaded region = $\left( {1200 - 600} \right)c{m^2}$ = $600c{m^2}$ 

81. 

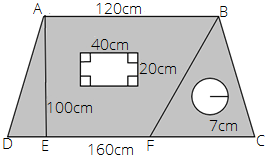
Ans: Area of shaded portion = area of trapezium – area of the rectangle – area of the circle

Area of trapezium = $\dfrac{1}{2} \times \left( \text{sum of parallel side} \right) \times \text{height}$ 

$ = \dfrac{1}{2} \times \left( {120 + 160} \right) \times 100$

$ = \dfrac{1}{2} \times \left( {280} \right) \times 100$

$ = 14000c{m^2}$

Area of rectangle = $l \times b$ = $40 \times 20$ = $800c{m^2}$ 

Area of circle = $\pi {r^2}$ = $\dfrac{{22}}{7} \times 7 \times 7$ = $154c{m^2}$ 

Therefore, area of shaded region = $14000c{m^2} - 800c{m^2} - 154c{m^2}$ = $13046c{m^2}$ 

82.

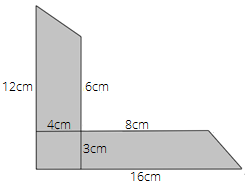
Ans: 

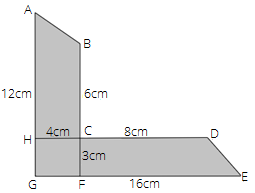
Area of shaded portion = area of trapezium ABCH + area of trapezium CDEF + area of rectangle CHGF

Area of trapezium = $\dfrac{1}{2} \times \left( \text{sum of parallel side} \right) \times \text{height}$ 

Area of trapezium ABCH = $\dfrac{1}{2} \times \left( {12 + 6} \right) \times 4$ 

$ = \dfrac{1}{2} \times 18 \times 4$

$ = 36c{m^2}$

Area of trapezium CDEF = $\dfrac{1}{2} \times \left( {8 + 16} \right) \times 3$ 

$ = \dfrac{1}{2} \times 24 \times 4$

$ = 36c{m^2}$

Area of rectangle CHGF = $l \times b$ = $4 \times 3$ = $12c{m^2}$ 

Therefore, area of shaded portion = $36 + 36 + 12$ = $84c{m^2}$ 

83. 

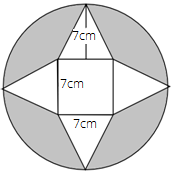
Ans: Area of shaded portion = Area of the circle $ - $ area of four triangles $ - $ area of a square.

Area of $4$ triangles = $4 \times \dfrac{1}{2} \times base \times height$ 

$ = 4 \times \dfrac{1}{2} \times 7 \times 7$

$ = 2 \times 49$

$ = 98c{m^2}$

Area of a square = ${\left( {side} \right)^2}$ = ${7^2}$ = $49c{m^2}$ 

Area of the circle = $\pi {r^2}$ = $\dfrac{{22}}{7} \times {\left( {\dfrac{{21}}{2}} \right)^2}$ 

$ = \dfrac{{11 \times 3 \times 21}}{2}$

$ = \dfrac{{693}}{2}$

$ = 346.5c{m^2}$

Area of shaded region = $346.5 - 98 - 49$ = $199.5c{m^2}$ 

84. 

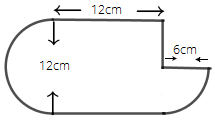
Ans:

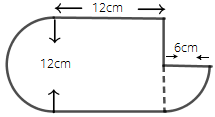
Area of the given figure = area of the section with $6cm$ + area of square with side measure $12cm$ + area of a semi-circle with radius $6cm$ 

$ = \dfrac{{22 \times 6 \times 6}}{{7 \times 4}} + {\left( {12} \right)^2} + \dfrac{{22 \times 6 \times 6}}{{7 \times 2}}$ 

$ = \dfrac{{11 \times 18}}{7} + 144 + \dfrac{{11 \times 36}}{7}$

$ = \dfrac{{198}}{7} + 144 + \dfrac{{396}}{7}$

$ = \dfrac{{198 + 1008 + 396}}{7}$

$ = \dfrac{{1602}}{7}$

$ = 228.85c{m^2}$

85. 

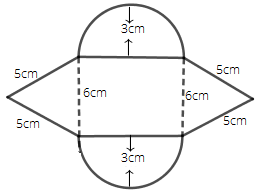
Ans: Area of the given figure = area of two semi-circles + area of two triangles + area of a square.

We will use Heron’s formula to find the area of the triangle.

Heron’s formula = $\sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $, where $s = \dfrac{{a + b + c}}{2}$. Therefore, we have

$ \Rightarrow s = \dfrac{{5 + 5 + 6}}{2}$

$ \Rightarrow s = \dfrac{{16}}{2}$

$ \Rightarrow s = 8cm$

Area of triangle = $\sqrt {8\left( {8 - 5} \right)\left( {8 - 5} \right)\left( {8 - 6} \right)} $

$ = \sqrt {8 \times 3 \times 3 \times 2} $

$ = \sqrt {144} $

$ = 12c{m^2}$

Therefore, the area of two triangles = $2 \times 12c{m^2}$ = $24c{m^2}$

Area of two semi-circles = area of one circle.

Area of a circle = $\pi {r^2}$ = $\dfrac{{22}}{7} \times 3 \times 3$ 

$ = \dfrac{{198}}{7}$

$ = 28.28c{m^2}$

Area of a square = $6 \times 6$ = $36c{m^2}$

Hence, the area of the given figure = $24 + 28.28 + 36$ = $88.28c{m^2}$ 

86. Find the volume of each of the given figures if volume = base area $ \times $ height.

a) 

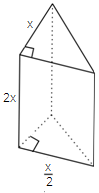
Ans: In the given figure, the base is rectangle. 

So, area of rectangle = $2x \times \dfrac{x}{2}$ = ${x^2}$ 

Thus, height = $x$ 

So, the volume of the figure = ${x^2} \times x$ = \[{x^3}\] 

b) 

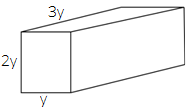
Ans: In the given figure, the base is rectangle.

So, area of rectangle = $y \times 3y$ = $3{y^2}$ 

Height = $2y$ 

Thus, volume of the figure = $3{y^2} \times 2y$ = $6{y^3}$ 

c) 

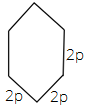
Ans: In the given figure, the base is rectangle.

So, area of rectangle = $2p \times 2p$ = $4{p^2}$ 

Height = $2p$ 

Volume of the figure = $4{p^2} \times 2p$ = $8{p^3}$ 

87. A cube of side $5cm$ is cut into as many $1cm$ cubes as possible. What is the ratio of the surface area of the original cube to that of the sum of the surface areas of the smaller cubes?

Ans: We know that volume of cube having side $a$ = ${a^3}$ 

Volume of original cube having side $5cm$ = ${5^3}$ = $125c{m^3}$ 

Volume of $1$ smaller cube = $1c{m^3}$

Number of small cubes = $\dfrac{\text{Volume of original cube}}{\text{Volume of 1 small cube}}$

$ = \dfrac{{125c{m^3}}}{{1c{m^3}}}$ 

Thus, the number of small cubes = $125$.

We know that surface area of cube having side $a$ = $6{a^2}$ 

We have a cube of side $5cm$

Thus, surface area = $6 \times {5^2}$=$6 \times 25$=$150c{m^2}$ 

Surface area of cube with side $1cm$ = $6 \times {1^2}$ = $6c{m^2}$

Hence, surface area of $125$ cubes having side $1cm$ = $125 \times 6$ = $750c{m^2}$

Therefore, ratio of the surface area of the original cube to that of the sum of the surface area of the smaller cubes = $\dfrac{{150}}{{750}}$ = $1:5$ 

88. A square sheet of paper is converted into a cylinder by rolling it along its side. What is the ratio of the base radius to the side of the square? 

Ans: Let $a$ be the side of a square paper.

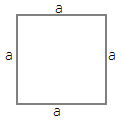
A cylinder is formed by rolling the paper along its side.

Thus, the base of a cylinder is a circle so the circumference of the circle is equal to the length of each side of the square sheet.

$ \Rightarrow 2\pi r = a$ 

$ \Rightarrow r = \dfrac{a}{{2\pi }}$

Therefore, ratio of the base radius to the side of the square = $\dfrac{{\dfrac{a}{{2\pi }}}}{a}$ 

$ = \dfrac{a}{{2\pi }} \times \dfrac{1}{a}$

$ = \dfrac{1}{{2\pi }}$

$ = 1:2\pi $

89. How many cubic meters of earth must be dug to construct a well $7m$ deep and of diameter $2.8m$ ?

Ans: A well is in cylindrical form.

Earth must be dug $7m$ deep to construct a well and be of diameter $2.8m$, is equal to the volume of the cylinder with height $7m$ and diameter $2.8m$

We know that volume of cylinder = $\pi {r^2}h$ 

$ = \dfrac{{22}}{7} \times \dfrac{{2.8}}{2} \times \dfrac{{2.8}}{2} \times 7$ 

\[ = 11 \times 2.8 \times 1.4\]

\[ = 43.12{m^3}\]

90. The radius and height of a cylinder are in the ratio $3:2$ and its volume is $19,404c{m^3}$. Find its radius and height. 

Ans: Let $3x$ be the radius and $2x$ be the height.

Given that, the volume of cylinder = $19,404c{m^3}$

We know that volume of cylinder = $\pi {r^2}h$ 

$ \Rightarrow 19,404 = \dfrac{{22}}{7} \times {\left( {3x} \right)^2} \times 2x$

$ \Rightarrow 19,404 = \dfrac{{22}}{7} \times 9{x^2} \times 2x$

$ \Rightarrow 19,404 = \dfrac{{22 \times 18{x^3}}}{7}$

$ \Rightarrow 19,404 = \dfrac{{396{x^3}}}{7}$

$ \Rightarrow {x^3} = \dfrac{{19,404 \times 7}}{{396}}$

$ \Rightarrow {x^3} = 343$

$ \Rightarrow {x^3} = {7^3}$

$ \Rightarrow x = 7$

Therefore, radius of the cylinder = $3 \times 7$ = $21cm$ 

And the height of the cylinder = $2 \times 7$ = $14cm$ 

91. The thickness of a hollow metallic cylinder is $2cm$. It is $70cm$ long with an outer radius of $14cm$. Find the volume of the metal used in making the cylinder, assuming that it is open at both the ends. Also find its weight if the metal weighs $8g$ per $c{m^3}$. 

Ans: We have,

The thickness of a hollow metallic cylinder = $2cm$.

Height of the cylinder = $70cm$

Outer radius = $14cm$

Inner radius = $14 - 2$ = $12cm$

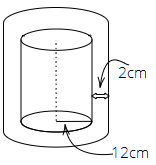
Volume of metal used in making the cylinder = volume of the hollow cylinder

$ = \pi \left( {{R^2} - {r^2}} \right) \times h$ 

$ = \dfrac{{22}}{7}\left( {{{14}^2} - {{12}^2}} \right) \times 70$

$ = 22\left( {196 - 144} \right) \times 10$

$ = 22 \times 52 \times 10$

$ = 11440c{m^3}$

Weight of $11440c{m^3}$, if metal is $8g$ per $c{m^3}$ = $11440 \times 8$ = $91520g$ 

92. Radius of a cylinder is $r$ and the height is $h$. Find the change in the volume if the

a) Height is doubled

Ans: We know that volume of cylinder having radius $r$ and height $h$ = $\pi {r^2}h$ 

If height is doubled, it becomes $2h$ 

Therefore, the volume = $\pi {r^2} \times 2h$ = $2\pi {r^2}h$

Hence, the volume becomes double of the original volume.

b) Height is doubled and the radius is halved

Ans: If the height is doubled, it becomes $2h$ and the radius is halved, it becomes $\dfrac{r}{2}$ 

Therefore, volume = $\pi {\left( {\dfrac{r}{2}} \right)^2} \times 2h$ 

$ = \pi  \times \dfrac{r}{2} \times \dfrac{r}{2} \times 2h$

$ = \dfrac{1}{2}\pi {r^2}h$

Hence, volume becomes half of the original volume.

c) Height remains same and the radius is halved. 

Ans: If height remains the same i.e. $h$ and the radius is halved, it becomes $\dfrac{r}{2}$

Therefore, volume = $\pi {\left( {\dfrac{r}{2}} \right)^2} \times h$ 

$ = \pi  \times \dfrac{r}{2} \times \dfrac{r}{2} \times h$

$ = \dfrac{1}{4}\pi {r^2}h$

Hence, the volume becomes $\dfrac{1}{4}th$ of the original volume.

93. If the length of each edge of a cube is tripled, what will be the change in its volume? 

Ans: Let $a$ be the edge of the cube.

We know that volume of a cube having side $a$ = ${a^3}$ 

If the edge of the cube became tripled, we get edge = $3a$ 

Therefore, volume of cube having edge $3a$ = ${\left( {3a} \right)^2}$ 

$ = 27{a^3}$ 

Hence, volume is $27$ times of the original volume.

94. A carpenter makes a box which has a volume of $13,400c{m^3}$. The base has an area of $670c{m^2}$. What is the height of the box? 

Ans: Let $h$ be the height of the box.

The volume of the box = $13400c{m^2}$ 

Area of base of the box = $670c{m^2}$

Since, the volume of the box = area of base $ \times $ height

Therefore, $13400 = 670 \times h$ 

$ \Rightarrow h = \dfrac{{13400}}{{670}}$

$ \Rightarrow h = 20cm$

95. A cuboidal tin box opened at the top has dimensions $20cm \times 16cm \times 14cm$. What is the total area of metal sheet required to make $10$ such boxes? 

Ans: Given that, dimensions of the tin box (opened at the top) = $20cm \times 16cm \times 14cm$

Total area of the metal sheet required to make it = lateral surface area + base area

$ = 2\left( {l + b} \right) \times h + lb$ 

$ = 2\left( {20 + 16} \right) \times 14 + 20 \times 16$

$ = \left( {2 \times 36 \times 14 + 20 \times 16} \right)c{m^2}$

$ = \left( {1008 + 320} \right)c{m^2}$

$ = 1328c{m^2}$

Hence, the area of the metal sheet required to make $10$ such boxes = $10 \times 1328$ = $13280c{m^2}$

96. Find the capacity of a water tank, in liters, whose dimensions are $4.2m$, $3m$ and $1.8m$ ?

Ans: Given that, dimensions of the water tank are $4.2m$, $3m$ and $1.8m$

The capacity of water tank = $4.2m \times 3m \times 1.8m$

$ = 22.68{m^3}$ 

Since, 1m3=1000 liter

So, Capacity of the water tank in liter $ = 22.68\times 1000 = 22680$ liter

97. How many cubes each side $0.5cm$ are required to build a cube of volume $8c{m^3}$ ? 

Ans: We know that volume of cube = ${\left( {side} \right)^3}$ 

Therefore, the volume of the cube having side $0.5cm$ = ${\left( {0.5} \right)^3}$ = $0.125c{m^3}$ 

Thus, the number of cubes required to make the volume of $8c{m^3}$ cube = $\dfrac{8}{{0.125}}$ 

$ = \dfrac{{8000}}{{125}}$

$ = 64$ cubes.

98. A wooden box (including the lid) has external dimensions $40cm$ by $34cm$ by $30cm$. If the wood is $1cm$ thick, how many $c{m^3}$ of wood is used in it? 

Ans: Given that, the external dimensions of the wooden box are $40cm \times 34cm \times 30cm$.

The wood is $1cm$ thick. 

Therefore, the internal dimensions of the wooden box will be $\left( {40 - 2} \right)cm \times \left( {34 - 2} \right)cm \times \left( {30 - 2} \right)cm$

$ = 38cm \times 32cm \times 28cm$

Thus, wood used for the box = volume of the wooden box with external dimensions $ - $ volume of wooden box with external dimensions

The wood used for the box = $40cm \times 34cm \times 30cm - 38cm \times 32cm \times 28cm$

The wood used for the box = $40800c{m^3} - 34048c{m^2}$

The wood used for the box = $6752c{m^3}$

99. A river $2m$ deep and $45m$ wide is flowing at the rate of $3km$ per hour. Find the amount of water in cubic meters that runs into the sea per minute.

Ans: Given that, depth of the river is $2m$ and the width of the river is $45m$

Flowing rate of water = $3km/h$ 

Let us first convert this into a meter per minute.

$ = 3 \times \dfrac{{1000}}{{60}}$ 

$ = \dfrac{{300}}{6}$

$ = 50m/\min $

The amount of water that runs into the sea per minute = depth $ \times $ width $ \times $ length of water of $1$ minute.

Thus, the amount of water that runs into the sea per minute = $2 \times 45 \times 50{m^3}/\min $ 

$ = 4500{m^3}/\min $

100. Find the area to be painted in the following block with a cylindrical hole. Given that length is $15cm$, width $12cm$, height $20cm$ and radius of the hole $2.8cm$.

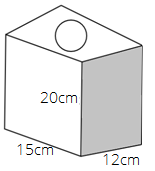
Ans: In the given figure, we have

Length = $15cm$ 

Width = $12cm$ 

Height = $20cm$ 

Radius of the hole = $2.8cm$

Therefore, the area to be painted = surface area of the figure $ - $ $2 \times $ area of a circular hole.

$ = 2\left( {lb + bh + hl} \right) - 2\pi {r^2}$ 

$ = 2\left( {15 \times 12 + 12 \times 20 + 15 \times 20} \right) - 2 \times \dfrac{{22}}{7} \times 2.8 \times 2.8$

$ = 2\left( {180 + 240 + 300} \right) - \dfrac{{2 \times 22 \times 2.8 \times 2.8}}{7}$

$ = 2\left( {720} \right) - 49.28$

$ = 1440 - 49.28$

$ = 1390.72c{m^2}$

101. A truck carrying $7.8{m^3}$ concrete arrives at a job site. A platform of width $5m$ and height $2m$ is being constructed at the site. Find the length of the platform, constructed from the amount of concrete on the truck?

Ans: Total volume of concrete = $7.8{m^3}$

Width of the platform = $5m$ 

Height of the platform = $2m$ 

Let the length of the platform be \[x{\text{ }}m\] 

According to the question, 

Volume used to make platform = volume of concrete

Therefore, we get

$ \Rightarrow x \times 5 \times 2 = 7.8$ 

$ \Rightarrow x \times 10 = 7.8$

$ \Rightarrow x = \dfrac{{7.8}}{{10}}$

$ \Rightarrow x = 0.78m$

Hence, the length of the platform, constructed from the amount of concrete on the truck is $0.78m$.

102. A hollow garden roller of $42cm$ diameter and length $152cm$ is made of cast iron $2cm$ thick. Find the volume of iron used in the roller. 

Ans: Diameter of hollow garden roller = $42cm$

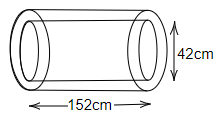
Thus, inner radius $r$ = $\dfrac{{42}}{2}cm$ = $21cm$ 

Thickness of iron cast = $2cm$

Therefore, outer radius $R$ = $21 + 2$ = $23cm$ 

Length of the garden roller = $152cm$

Volume of the hollow cylinder = $\pi \left( {{R^2} - {r^2}} \right) \times h$ 

On substituting the values, we get

$= \dfrac{{22}}{7}\left[ {{{\left( {23} \right)}^2} - {{\left( {21} \right)}^2}} \right] \times 152$

$= \dfrac{{22}}{7}\left[ {529 - 441} \right] \times 152$

$= \dfrac{{22}}{7} \times 88 \times 152$

$= \dfrac{{294272}}{7}$

$= 42038.85c{m^3}$

Therefore, the volume of iron used in the roller is $42038.85c{m^3}$

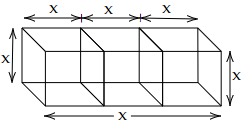
103. Three cubes each side $10cm$ are joined end to end. Find the surface area of the resultant figure. 

Ans: If we join three cubes each side $10cm$, then a cuboid will be formed of dimensions $30 \times 10 \times 10$.

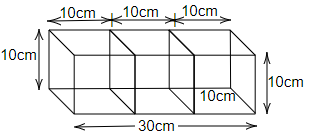
We know that the surface area of the cuboid = $2\left( {lb + bh + hl} \right)$ 

$ = 2\left( {30 \times 10 + 10 \times 10 + 30 \times 10} \right)$ 

$ = 2\left( {300 + 100 + 300} \right)$

$ = 2 \times 700$

$ = 1400c{m^2}$

104. Below are the drawings of cross-sections of two different pipes used to fill swimming pools. Figure A is a combination of $2$ pipes each having a radius of $8cm$. Figure B is a pipe having a radius of $15cm$. If the force of the flow of water coming out of the pipes is the same in both cases, which will fill the swimming pool faster?

Ans: In figure A, $2$ pipes each having a radius of $8cm$ 

We know that area of circle = $\pi {r^2}$ 

Area of one pipe = $\dfrac{{22}}{7} \times 8 \times 8$ = $\dfrac{{22 \times 64}}{7}c{m^2}$

Therefore, area of two pipes = $\dfrac{{2 \times 1408}}{7}c{m^2}$ = $\dfrac{{2816}}{7}c{m^2}$ = $402.28c{m^2}$ 

In figure B, a pipe having radius of $15cm$

Area of pipe = $\dfrac{{22}}{7} \times 15 \times 15$ = $\dfrac{{22 \times 225}}{7}c{m^2}$

$ = \dfrac{{4950}}{7}c{m^2}$

$ = 707.14c{m^2}$

The surface area of pipe B is greater so pipe B fills the swimming pool faster.

105. A swimming pool is $200m$ by $50m$ and has an average depth of $2m$. By the end of a summer day, the water level drops by $2cm$. How many cubic meters of water is lost on the day?

Ans: We have,

Dimensions of swimming pool = $200m \times 50m$ 

Average depth of swimming pool = $2m$

At the end of summer day the water level drops by $2cm$

Thus, volume of water in swimming pool = length × breadth ×depth

$ = 200 \times 50 \times 2$ 

$ = 20000{m^3}$

If the level drops by $2cm$. New water level is $\left( {2 - \dfrac{2}{{100}}} \right)m$ 

$ = 1.98m$ 

Therefore, the volume of water after summer day = $200m \times 50m \times 1.98m$

$ = 19800{m^3}$

Hence, water in cubic meters was lost on that day = initial volume $ - $ volume after summer day

$ = 20000 - 19800$

$ = 200{m^3}$

106. A housing society consisting of $5,500$ people needs $100L$ of water per person per day. The cylindrical supply tank is $7m$ high and has a diameter $10m$. For how many days will the water in the tank last for the society? 

Ans: Given that, the total number of people = $5,500$

Water required per person per day = $100L$

Therefore, total water requirement by $5,500$ people = $100 \times 5500$ = $550000L/day$

Height of cylindrical tank = $7m$

Diameter of cylindrical tank = $10m$

Therefore, radius = $5m$

Volume of cylinder = $\pi {r^2}h$ 

$ = \dfrac{{22}}{7} \times 5 \times 5 \times 7$ 

$ = 22 \times 25$

$ = 550{m^3}$

As $1{m^3} = 1000L$. Therefore, we get

$ = 550 \times 1000$

$ = 550000L$

Time taken to empty the water tank = $\dfrac{\text{Total capacity of water tank}}{\text{Total requirement of water}}$ 

$ = \dfrac{{550000L}}{{550000L/day{\text{ }}}}$

$ = 1day$ 

Hence, in society, the water in the tank will last of $1$ day.

107. Metallic discs of radius $0.75cm$ and thickness $0.2cm$ are melted to obtain $508.68c{m^3}$ of metal. Find the number of discs melted (use $\pi  = 3.14$ ). 

Ans:

Given that,

The radius of metallic disc = $0.75cm$

The thickness of metallic disc = $0.2cm$

Total volume of metal obtained after melting discs = $508.68c{m^3}$

Therefore, material required for one disc = volume of cylinder = $\pi {r^2}h$ 

$ = \dfrac{{22}}{7} \times 0.75 \times 0.75 \times 0.2$ 

$ = 0.35325c{m^3}$

Number of discs melted = $\dfrac{{Total{\text{ }}volume{\text{ }}of{\text{ }}metal{\text{ }}obtained{\text{ }}after{\text{ }}melting{\text{ }}discs}}{{volume{\text{ }}of{\text{ }}one{\text{ }}disc}}$ 

$ = \dfrac{{508.68}}{{0.35325}}$

$ = 1440$ discs.

108. The ratio of the radius and height of a cylinder is $2:3$. If its volume is $12,936c{m^3}$, find the total surface area of the cylinder. 

Ans: Let $2x$ be the radius and $3x$ be the height of the cylinder.

We know that volume of cylinder having radius $r$ and height $h$ = $\pi {r^2}h$ 

Therefore,

$ \Rightarrow 12936 = \dfrac{{22}}{7} \times {\left( {2x} \right)^2} \times 3x$

$ \Rightarrow 12936 = \dfrac{{22}}{7} \times 4{x^2} \times 3x$

$ \Rightarrow 12936 = \dfrac{{264}}{7}{x^3}$

$ \Rightarrow {x^3} = \dfrac{{12936 \times 7}}{{264}}$

$ \Rightarrow {x^3} = 343$

$ \Rightarrow {x^3} = {7^3}$

$ \Rightarrow x = 7$

109. External dimensions of a closed wooden box are in the ratio $5:4:3$. If the cost of painting its outer surface at the rate of Rs $5$ per $d{m^2}$ is Rs $11,750$, find the dimensions of the box. 

Ans: Given that, external dimensions of a closed wooden box are in the ratio $5:4:3$.

Let the external dimensions of the closed wooden box be $5x$, $4x$ and $3x$.

The cost of painting = Rs $5$ per $d{m^2}$ 

Total cost of painting = Rs $11,750$

Therefore, total surface area = total cost of painting/cost of painting per $d{m^2}$

$ = \dfrac{{11750}}{5}$ 

$ = 2350d{m^2}$

The total surface area of a cuboid = $2\left( {lb + bh + hl} \right)$ 

$ = 2\left( {5x \times 4x + 4x \times 3x + 3x \times 5x} \right)$

$ = 2\left( {20{x^2} + 12{x^2} + 15{x^2}} \right)$

$ = 2 \times 47{x^2}$

\[ = 94{x^2}\]

Since the total surface area is $2350d{m^2}$. Therefore, we get

\[ \Rightarrow 94{x^2} = 2350\]

\[ \Rightarrow {x^2} = \dfrac{{2350}}{{94}}\]

\[ \Rightarrow {x^2} = 25\]

\[ \Rightarrow x = 5\]

Hence, the dimensions of the box are

$ \Rightarrow 5x = 5 \times 5 = 25dm$ 

\[ \Rightarrow 4x = 4 \times 5 = 20dm\]

$ \Rightarrow 3x = 3 \times 5 = 15dm$

110. The capacity of a closed cylindrical vessel of height $1m$ is $15.4L$. How many square meters of metal sheet would be needed to make it? 

Ans: Given that,

Height of cylindrical vessel = $1m$

Capacity of cylindrical vessel = $15.4L$

In meter cube = $\dfrac{{15.4}}{{1000}}$ = $0.0154{m^3}$ 

Volume of the cylinder = $\pi {r^2}h$ 

$ \Rightarrow \dfrac{{22}}{7} \times {r^2} \times 1 = 0.0154$

$ \Rightarrow {r^2} = \dfrac{{0.0154}}{{3.14}}$

$ \Rightarrow {r^2} = 0.0049$

$ \Rightarrow r = \sqrt {0.0049} $

$ \Rightarrow r = 0.07m$

Thus, required metal sheet = $2\pi rh$ 

$= 2 \times \dfrac{{22}}{7} \times 0.07 \times 1$

$= 0.44{m^3}$

111. What will happen to the volume of the cube, if its edge is 

a) Tripled

Ans: We know that volume of cube having side $a$ = ${a^3}$ 

If the side becomes triple, the volume will be ${\left( {3a} \right)^3}$ = $27{a^3}$ 

Hence, the new volume is $7$ times the original volume.

b) Reduced to one-fourth? 

Ans: If side is reduced to one fourth i.e. $\dfrac{a}{4}$ 

Volume = ${\left( {\dfrac{a}{4}} \right)^3}$ = $\dfrac{1}{{64}}{a^3}$ 

Hence, the new volume is $\dfrac{1}{{64}}$ times the original volume.

112. A rectangular sheet of dimensions $25cm \times 7cm$ is rotated about its longer side. Find the volume and the whole surface area of the solid thus generated. 

Ans: A rectangular sheet of dimensions $25cm \times 7cm$ is rotated about its longer side which makes a cylinder with base $25cm$ and height $7cm$.

Thus, surface area of base = $2\pi r$ 

So, $2\pi r = 25$ 

$ \Rightarrow r = \dfrac{{25 \times 7}}{{2 \times 22}}$

$ \Rightarrow r = \dfrac{{175}}{{44}}cm$

Volume of the cylinder = $\pi {r^2}h$ 

$ = \dfrac{{22}}{7} \times \dfrac{{175}}{{44}} \times \dfrac{{175}}{{44}} \times 7$ 

$ = \dfrac{{175 \times 175}}{{2 \times 44}}$

$ = \dfrac{{30625}}{{88}}$

$ = 348.011c{m^3}$

Surface area = $2\pi rh$ 

$ = 2 \times \dfrac{{22}}{7} \times \dfrac{{175}}{{44}} \times 7$ 

$ = \dfrac{{44 \times 175}}{{44}}$

$ = 175c{m^2}$ 

113. From a pipe of inner radius $0.75cm$, water flows at the rate of $7m$ per second. Find the volume in liters of water delivered by the pipe in $1$ hour. 

Ans: Given that, the radius of pipe = $0.75cm$ = $0.0075m$

Rate of water flow = $7m/s$

Therefore, length of water in $1$ sec = $7m$

Thus, the volume of water flow in $1$ hour = $60 \times 60 \times \dfrac{{22}}{7} \times 0.0075 \times 0.0075 \times 7$ 

\[ = 3600 \times 3.14 \times 0.00005625 \times 7\]

\[ = 79128 \times 0.00005625\]

\[ = 4.45095{m^3}\]

\[ = 4450000c{m^3}\]

\[ = 4450L\]

114. Four times the area of the curved surface of a cylinder is equal to $6$ times the sum of the areas of its bases. If its height is $12cm$, find its curved surface area. 

Ans: We know that curved surface area of cylinder having radius $r$ and height $h$ = $2\pi rh$ 

Area of base = $\pi {r^2}$ 

Sum of areas of bases = $2\pi {r^2}$

We have,

$4$ × curved surface area = $6$ × sum of areas of bases

$ \Rightarrow 4 \times 2\pi rh = 6 \times 2\pi {r^2}$ 

$ \Rightarrow 2h = 3r$

$ \Rightarrow r = \dfrac{{2h}}{3}$

Substitute height = $12cm$

$ \Rightarrow r = \dfrac{{2 \times 12}}{3}$

$ \Rightarrow r = 8cm$

Therefore, curved surface area = $2\pi rh$ 

$ = 2 \times \dfrac{{22}}{7} \times 8 \times 12$

$ = 603.428c{m^2}$

115. A cylindrical tank has a radius of $154cm$. It is filled with water to a height of $3m$. If water to a height of $4.5m$ is poured into it, what will be the increase in the volume of water in $kl$ ? 

Ans: Given that, radius of cylindrical tank = $154cm$

Initial height of water tank = $3m$ = $3 \times 100cm$ 

Therefore, volume of water = $\pi {r^2}h$

$ = \dfrac{{22}}{7} \times 154 \times 154 \times 3 \times 100$ 

$ = 22360800c{m^3}$

If the height of water $4.5m$ is poured into it, then the volume of water = $\dfrac{{22}}{7} \times 154 \times 154 \times 4.5 \times 100$ 

$ = 33541200c{m^3}$

Increase in volume = $33541200 - 22360800$

$ = 11180400c{m^3}$

$ = 11180.4L$

$ = 11.1804KL$

116. The length, breadth and height of a cuboidal reservoir is $7m$, $6m$ and $15m$ respectively. $8400L$ of water is pumped out from the reservoir. Find the fall in the water level in the reservoir. 

Ans: Given that,

Length of cuboid reservoir = $7m$

Breadth of cuboid reservoir = $6m$

Height of cuboid reservoir = $15m$

Capacity of cuboid reservoir = $l \times b \times h$ 

$ = 7 \times 6 \times 15$ 

$ = 630{m^3}$

If $8400L$ of water is pumped out.

In meter cubic = $\dfrac{{8400}}{{1000}}$ = $8.4{m^3}$ 

Thus, fall in water level = $630 - 8.4$ = $621.6{m^3}$ 

$ = 621.6 \times 1000$

$ = 621600L$

117. How many bricks of size $22cm \times 10cm \times 7cm$ are required to construct a wall $11m$ long, $3.5m$ high and $40cm$ thick, if the cement and sand used in the construction occupy ${\left( {1/10} \right)^{th}}$ part of the wall?

Ans: Volume of each brick = $22cm \times 10cm \times 7cm$

$ = 1540c{m^3}$ 

$ = 0.00154{m^3}$

Volume of wall = $11m \times 3.5m \times \dfrac{{40}}{{100}}m$

$ = 11m \times 3.5m \times 0.4m$

$ = 15.4{m^3}$

If ${\left( {1/10} \right)^{th}}$ part of the wall used in cement and sand, then part of wall used by remaining cement and sand = $\dfrac{{15.4}}{{10}}{m^3}$ 

$ = 1.54{m^3}$

Remaining part = $15.4{m^3} - 1.54{m^3}$ = $13.86{m^3}$

Thus, number of bricks = Volume of the wall to be consumed / Volume of each brick

$ = \dfrac{{13.86}}{{0.00154}}$ 

$ = 9000$

118. A rectangular examination hall having seats for $500$ candidates has to be built so as to allow $4$ cubic meters of air and $0.5$ square meters of floor area per candidate. If the length of the hall be $25m$, find the height and breadth of the hall. 

Ans: Total number of seats in rectangular examination hall = $500$

Length of the hall = $25m$

Cubic meter of air for per candidate = $4{m^3}$ 

Square meters of floor area for per candidate = $0.5{m^3}$

Therefore, the height of the hall = Volume of air per candidate / Square meter of floor for $1$ candidate.

$ = \dfrac{4}{{0.5}}$ 

$ = 8m$

Total capacity of the hall = $500 \times 4$ = $2000{m^3}$ 

Hence, breadth of the hall = $\dfrac{{2000}}{{25 \times 8}}$ = $10m$ 

119. The ratio between the curved surface area and the total surface area of a right circular cylinder is $1:2$. Find the ratio between the height and radius of the cylinder. 

Ans: We know that curved surface area of cylinder having radius $r$ and height $h$ = $2\pi rh$ 

And, total surface area of cylinder having radius $r$ and height $h$ = $2\pi r\left( {r + h} \right)$ 

The ratio between the curved surface area and total surface area of a cylinder is $1:2$. Therefore, we get

$ \Rightarrow \dfrac{{2\pi rh}}{{2\pi r\left( {r + h} \right)}} = \dfrac{1}{2}$ 

$ \Rightarrow \dfrac{h}{{r + h}} = \dfrac{1}{2}$

On cross-multiplication, we get

$ \Rightarrow 2h = r + h$

$ \Rightarrow 2h - h = r$

$ \Rightarrow h = r$

Hence, the ratio of height and radius = $1:1$.

120. A birthday cake has two tiers as shown in the figure below. Find the volume of the cake.

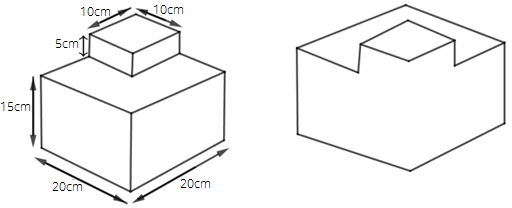
Ans: Volume of the cake = Volume of lower cuboid + Volume of upper cuboid

$ = 20 \times 20 \times 15 + 10 \times 10 \times 5$ 

$ = 6000 + 500$

$ = 6500c{m^3}$

Work out the surface area of the following shapes in question $121$ to $124$. (Use $\pi  = 3.14$ )

121. 

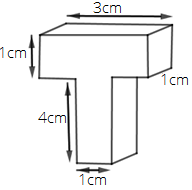
Ans: Surface area of the figure = 

$ = 2\left( {3 \times 1 + 1 \times 1 + 3 \times 1} \right) + 2\left( {4 \times 1 + 1 \times 1 + 4 \times 1} \right) - \left( {1 \times 1 + 1 \times 1} \right)$ 

\[ = 2\left( {3 + 1 + 3} \right) + 2\left( {4 + 1 + 4} \right) - \left( {1 + 1} \right)\]

\[ = 2\left( 7 \right) + 2\left( 9 \right) - \left( 2 \right)\]

\[ = 14 + 18 - 2\]

\[ = 30c{m^2}\]

122. 

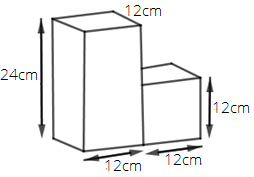
Ans: In the given figure, there are two cuboids joined. Therefore, total surface area of the given solid = 

$ = 2\left( {24 \times 12 + 12 \times 12 + 12 \times 24} \right) + 2\left( {12 \times 12 + 12 \times 12 + 12 \times 12} \right) - 2\left( {12 \times 12} \right)$ 

$ = 1440 + 864 - 288$

\[ = 2016c{m^2}\]

123. 

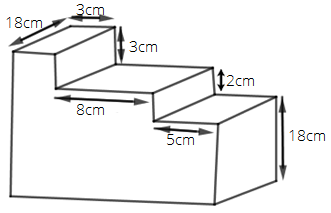
Ans: 

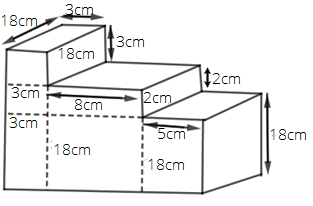
At first we will find the upper surface area. Therefore, we get

Upper surface area = $\left( {18 \times 3 + 8 \times 18 + 5 \times 18} \right)c{m^2}$ 

$ = \left( {54 + 144 + 90} \right)c{m^2}$

$ = 288c{m^2}$

Lower surface area = $288c{m^2}$

Surface area of those faces which are flat from right = $18 \times 18 + 2 \times 18 + 3 \times 18$ 

$ = \left( {324 + 36 + 54} \right)c{m^2}$

$ = 414c{m^2}$

Also, surface area of that face which are flat from right = $414c{m^2}$

Surface area of front face = $18 \times 5 + 2 \times 8 + 8 \times 18 + 3 \times 2 + 3 \times 18 + 3 \times 3$ 

$ = \left( {90 + 16 + 144 + 6 + 54 + 9} \right)c{m^2}$

$ = 319c{m^2}$

Surface area of back face = $319c{m^2}$

Therefore, total surface area = $288 + 288 + 414 + 414 + 319 + 319$ 

$ = 2042c{m^2}$

124. 

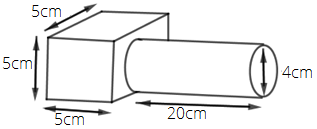
Ans: In the given figure, we have

Cube of side $5cm$ and cylinder of height $20cm$ and radius $2cm$.

So, total surface area of the given figure = surface area of the cube $\left( {6{a^2}} \right)$ $ + $ curved surface area of cylinder $\left( {2\pi rh} \right)$ 

Total surface area = $6{\left( 5 \right)^2} + 2\pi  \times 2 \times 20$ 

Total surface area = $6 \times 25 + 80\pi $ 

Now, we will substitute the value $\pi  = 3.14$ 

Total surface area = $150 + 80 \times 3.14$ 

Total surface area = $150 + 251.2$ 

Total surface area = $401.2c{m^2}$ 

125. Water flows from a tank with a rectangular base measuring $80cm$ by $70cm$ into another tank with a square base of side $60cm$. If the water in the first tank is $45cm$ deep, how deep will it be in the second tank?

Ans: Given that, dimensions of rectangular base tank are $80cm \times 70cm$ 

Height of rectangular base tank = $45cm$ 

Each side of square base tank = $60cm$ 

Let the height of rectangular base tank be $h$ 

Volume of square tank = Volume of rectangular tank

$ \Rightarrow 60 \times 60 \times h = 80 \times 70 \times 45$ 

$ \Rightarrow h = \dfrac{{80 \times 70 \times 45}}{{60 \times 60}}$

$ \Rightarrow h = 70cm$

Therefore, water in the second tank will be $70cm$ deep.

126. A rectangular sheet of paper is rolled in two different ways to form two different cylinders. Find the volume of cylinders in each case if the sheet measures $44cm \times 33cm$.

(i). 

Ans: Case: 1 If sheet is rolled along $44cm$

$ \Rightarrow 2\pi r = 44cm$ 

Divide the equation by $2$ 

$ \Rightarrow \pi r = 22cm$

$ \Rightarrow r = \dfrac{{22}}{\pi }cm$

Substitute value of $\dfrac{1}{\pi } = \dfrac{7}{{22}}$ 

$ \Rightarrow r = 22 \times \dfrac{7}{{22}}cm$

$ \Rightarrow r = 7cm$

Volume of cylinder = $\pi {r^2}h$ = $\dfrac{{22}}{7} \times 7 \times 7 \times 33$ 

$ = 22 \times 33 \times 7c{m^3}$ 

$ = 5082c{m^3}$

(ii). 

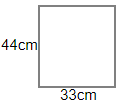
Ans: Case: 2 If sheet is rolled along $33cm$ 

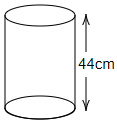
$ \Rightarrow 2\pi r = 33cm$ 

Divide the equation by $2$ 

$ \Rightarrow \pi r = \dfrac{{33}}{2}cm$

$ \Rightarrow r = \dfrac{{33}}{{2\pi }}cm$

Substitute value of $\dfrac{1}{\pi } = \dfrac{7}{{22}}$ 

$ \Rightarrow r = \dfrac{{33}}{2} \times \dfrac{7}{{22}}cm$

$ \Rightarrow r = \dfrac{{21}}{4}cm$

Volume of cylinder = $\pi {r^2}h$ = $\dfrac{{22}}{7} \times \dfrac{{21}}{4} \times \dfrac{{21}}{4} \times 44$ 

$ = \dfrac{{22 \times 3 \times 21 \times 11}}{4}c{m^3}$ 

$ = 3811.5c{m^3}$

The chapter deals with the concepts of measuring the area and volumes of various 2D and 3D figures like Trapezium, cube, and cuboids. Students get to learn many new formulas to calculate areas and volumes of various 3D figures. The chapter contains a lot of formulas used in it, so the students have to put extra effort to memorize all these formulas.

Mensuration is an important chapter for students of Class 8 and carries a weightage of 15 marks in the exams. Hence the student must practice this chapter thoroughly. Let us discuss the major topics covered in the chapter Mensuration.

The first major topic to appear in this chapter is Trapezium. The student gets to know a lot about trapezium and its properties, how to calculate their areas and perimeter. They also get to learn the derivation of the area of a trapezium and the application of the same.

After trapeziums, the next in the list is the concepts regarding Quadrilaterals, their properties, and the area of a quadrilateral. The area of the polynomial is taught in this part too.

Then the chapters come into the realm of 3D figures. Surface areas of Cubes, cuboids, and cylinders are dealt with in this portion. After surface areas, the last important topic is the Volume and Capacity of various 3D figures such as Cylinders. 

All of this can be a little tough in the beginning but after some practice, the chapter becomes easy to do. Practice as much as you can, especially for this chapter if you want to ace your examinations. You will be able to find all the necessary study material for free at Vedantu’s official website.