Class 9 Gravitation – Exercise-wise Questions and Answers
NCERT Solutions for Class 9 Science Chapter 9 Gravitation 2025-26
FAQs on NCERT Solutions for Class 9 Science Chapter 9 Gravitation 2025-26
1. How do the NCERT Solutions for Class 9 Science Chapter 9 help in preparing for the 2025-26 exams?
These solutions provide a detailed, step-by-step approach to solving every in-text and exercise question from the CBSE 2025-26 syllabus. By using them, you can learn the correct format for writing answers, understand the application of formulas like the Universal Law of Gravitation, and grasp key concepts such as free fall, buoyancy, and the difference between mass and weight, which are crucial for scoring well in exams.
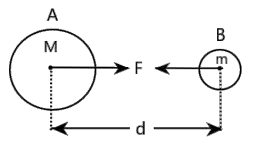
2. What is the correct method to state the Universal Law of Gravitation as per the NCERT textbook?
According to the NCERT solution, the Universal Law of Gravitation states that every object in the universe attracts every other object with a force. This force is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centres. The formula to find the magnitude of this force (F) is given by F = G(Mm)/d², where G is the universal gravitational constant.
3. How do you solve the NCERT problem calculating the gravitational force between the Earth and a 1 kg object on its surface?
The solution requires using the formula F = G(Mm)/R². The step-by-step method is as follows:
- Identify the given values: Mass of Earth (M) = 6 × 10²⁴ kg, mass of the object (m) = 1 kg, and Radius of Earth (R) = 6.4 × 10⁶ m.
- Use the value of the Universal Gravitational Constant (G) = 6.67 × 10⁻¹¹ Nm²kg⁻².
- Substitute these values into the formula.
- The calculation shows that the gravitational force is 9.8 N.
4. What is the key difference between the mass of an object and its weight, as explained in the Chapter 9 solutions?
The NCERT solutions clarify the following key differences:
- Mass is the measure of the amount of matter in an object and is constant everywhere. Its SI unit is the kilogram (kg).
- Weight is the gravitational force exerted on an object (W = mg) and it changes depending on the acceleration due to gravity (g). Its SI unit is the Newton (N).
- Mass can never be zero, whereas an object's weight can be zero in a place with no gravity.
5. Why does the NCERT solution state that a heavy object does not fall faster than a light object?
This is a common misconception. The NCERT solution explains that all objects, regardless of their mass, fall towards the Earth with a constant acceleration known as the acceleration due to gravity (g ≈ 9.8 m/s²), assuming no air resistance. Since the acceleration is the same for all objects, a heavy object and a light object will fall at the same rate and reach the ground at the same time if dropped from the same height.
6. How does the NCERT solution explain why it is difficult to hold a school bag with a thin strap?
The solution explains this using the concept of pressure. Pressure is defined as force per unit area (P = F/A). A thin strap has a very small surface area. This small area exerts a very high pressure on the shoulder for the same amount of force (the weight of the bag). A wider strap distributes the same force over a larger area, resulting in less pressure and making it more comfortable to carry.
7. Why is the weight of an object on the moon 1/6th of its weight on Earth, according to the NCERT derivation?
The NCERT solution derives this by comparing the gravitational forces on the Earth and the Moon. The weight of an object (W = mg) depends on the mass (M) and radius (R) of the celestial body. The Moon's mass is much smaller than Earth's, and its radius is also smaller. When the values for the Moon's mass and radius are substituted into the formula for gravitational force, the resulting force is calculated to be approximately 1/6th that of Earth's, hence the weight is also 1/6th.
8. What is the step-by-step method to solve the NCERT problem where a stone is released from a tower of height 19.6 m?
To find the final velocity just before it touches the ground, you must use the third equation of motion: v² - u² = 2gh. The steps are:
- The stone is released, so the initial velocity (u) is 0.
- The height (h) is given as 19.6 m.
- The acceleration due to gravity (g) is +9.8 m/s² (positive as it's falling downwards).
- Substituting these values, you get v² = 2 × 9.8 × 19.6, which simplifies to v² = (19.6)².
- Therefore, the final velocity (v) is 19.6 m/s.
9. How do you determine if a substance will float or sink based on the NCERT exercise involving a 50g substance with a volume of 20 cm³?
The solution is based on comparing the density of the substance with the density of water. The correct method is:
- First, calculate the density of the substance: Density = Mass/Volume = 50 g / 20 cm³ = 2.5 g/cm³.
- Next, compare this to the density of water, which is 1 g/cm³.
- Since the substance's density (2.5 g/cm³) is greater than the density of water, the substance will sink.
10. If the Moon attracts the Earth, why doesn't the Earth move towards the Moon? What is the NCERT explanation for this?
The NCERT solution explains this using Newton's Second Law of Motion (a = F/m). While the gravitational forces are equal and opposite, the masses of the Earth and Moon are vastly different. The Earth has a much larger mass than the Moon. Because acceleration is inversely proportional to mass, the same force produces a very large acceleration in the Moon but an extremely small, negligible acceleration in the Earth. This is why the Earth does not appear to move towards the Moon.
11. In the NCERT problem about Amit buying gold at the poles, why would his friend at the equator disagree with its weight?
The solution to this higher-order thinking question lies in the Earth's shape and its effect on gravity. The Earth is not a perfect sphere; it is flattened at the poles and bulges at the equator. This means the radius is smaller at the poles. Since acceleration due to gravity (g) is inversely proportional to the square of the radius (g ∝ 1/R²), the value of 'g' is slightly greater at the poles than at the equator. Therefore, the gold's weight (W = mg) would be slightly more at the poles than at the equator, causing the friend to disagree.














 Watch Video
Watch Video