Class 9 Maths Chapter 10 Summary Notes PDF Download
FAQs on Herons Formula Class 9 Maths Chapter 10 CBSE Notes - 2025-26
1. What are the key concepts summarized in Class 9 Maths Chapter 10 Revision Notes on Heron's Formula?
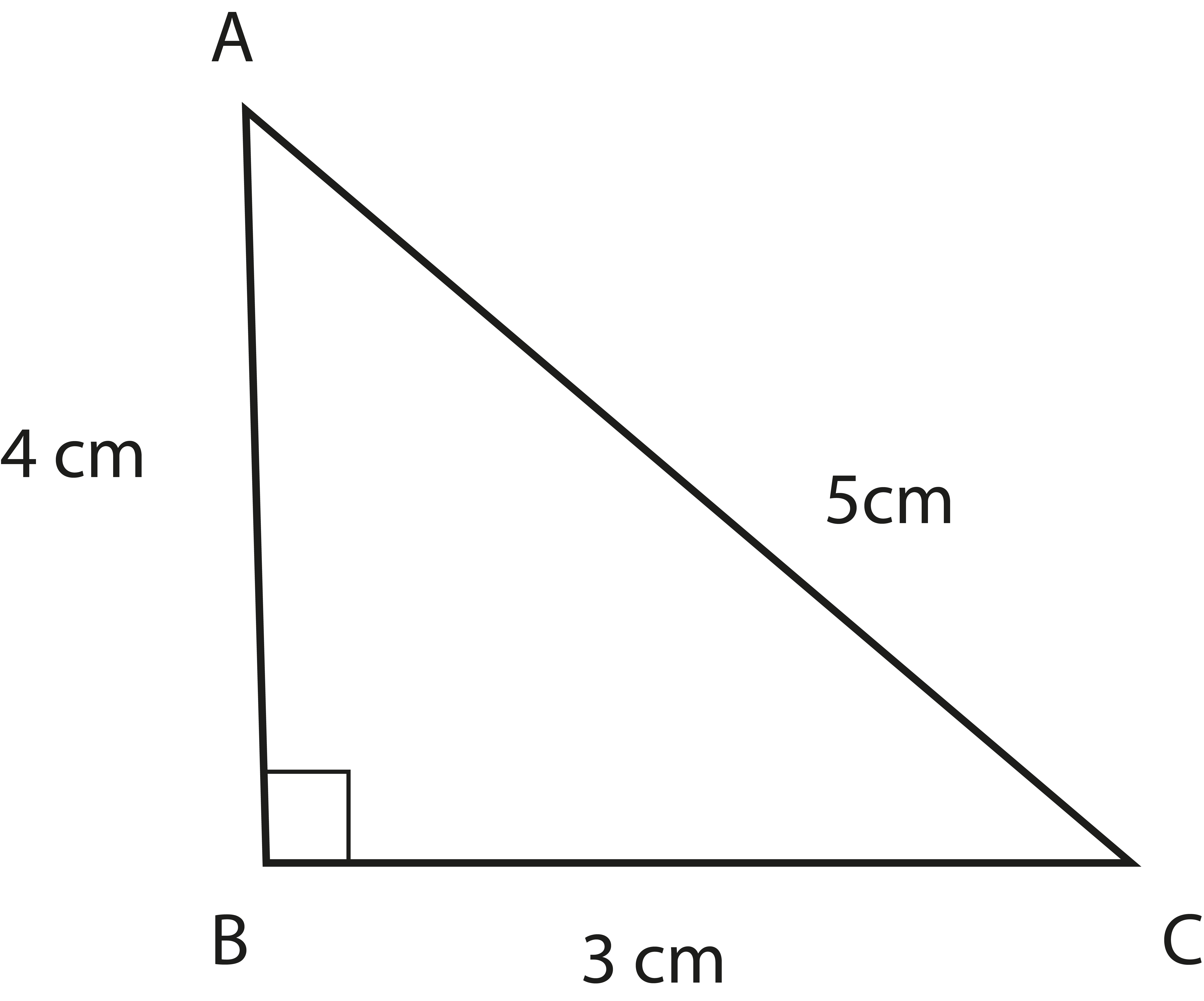
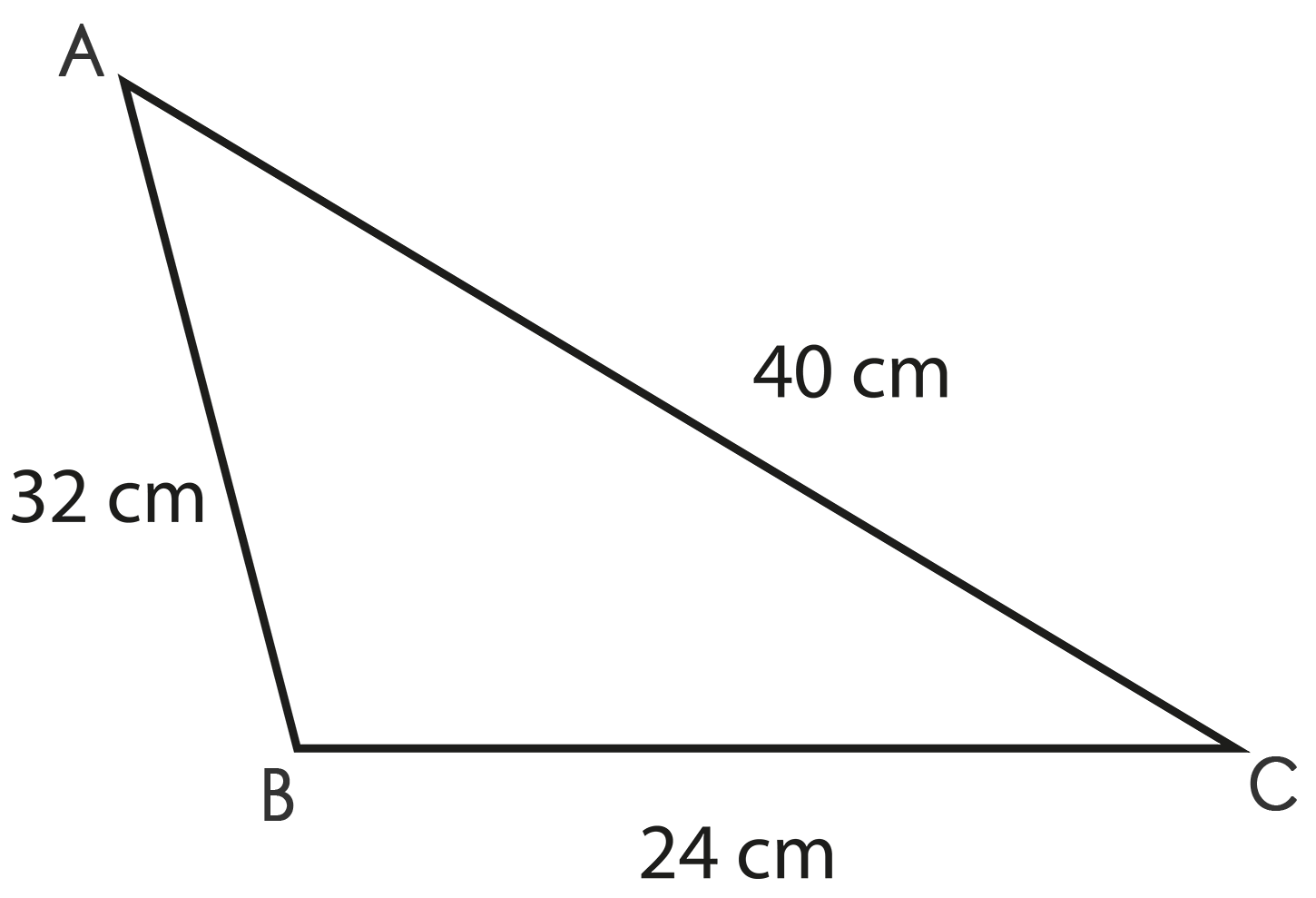
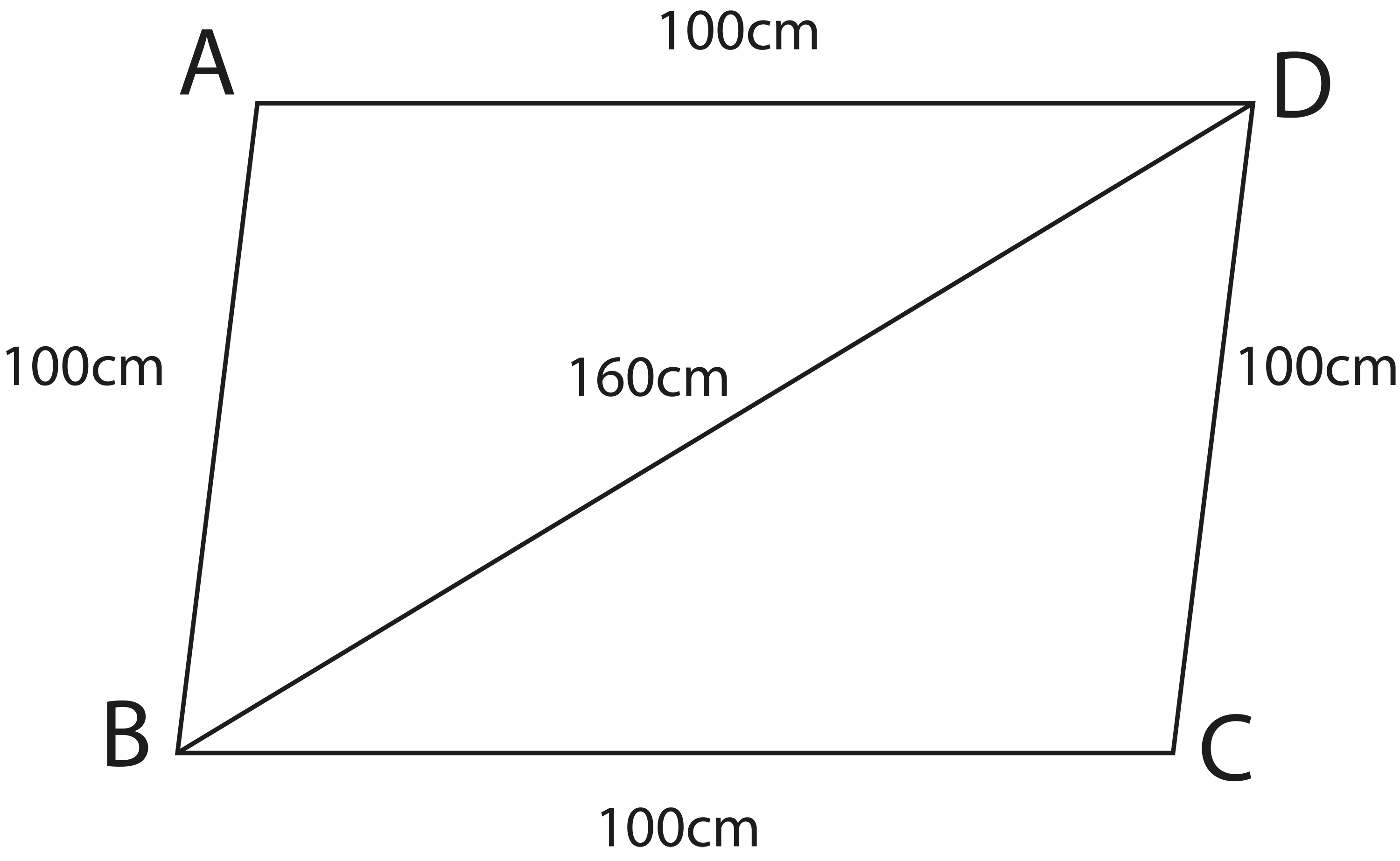
The revision notes for Chapter 10, Heron's Formula, focus on the definition and application of Heron's Formula to find the area of a triangle when the lengths of all sides are given, the meaning and calculation of semi-perimeter, and the method to calculate the area of a quadrilateral by dividing it into two triangles. They also cover quick formula recall for both height-based and side-based area calculations.
2. How can students structure their revision for Heron's Formula to cover all important concepts efficiently?
Students should start by reviewing the basic area formulas for triangles when the base and height are known, then move to understanding the derivation and use of Heron's Formula for cases where sides are given. Finally, focus on practice questions that apply Heron’s Formula to triangles and quadrilaterals. Revising key terms like semi-perimeter and perimeter will further aid quick recall during exams.
3. Why is Heron's Formula considered important for quick revision before exams?
Heron's Formula provides a direct way to calculate the area of triangles when the height is not available or difficult to measure, such as in scalene triangles. For quick revision, it saves time by offering a standard procedure, allowing students to solve a wide variety of geometry questions confidently and accurately in exams.
4. What is the quickest way to remember the formulas associated with Heron's Formula during last-minute revision?
Remember these key steps:
- First, calculate the semi-perimeter: s = (a + b + c) / 2
- Second, apply Heron’s Formula: Area = √[s(s−a)(s−b)(s−c)]
5. How does the revision of Heron's Formula interconnect with other chapters in Class 9 Maths?
Heron's Formula links to previous chapters on triangles, perimeter, and basic geometry. It also connects to quadrilaterals by using triangle area formulas, supporting students in solving complex shapes by breaking them into triangles, which enhances overall geometry problem-solving skills.
6. What are the essential terms to focus on when revising Heron's Formula?
Focus on understanding the terms:
- Semi-perimeter (s)
- Perimeter
- Area
- The roles of each side (a, b, c) in a triangle
- Application of the square root in Heron's Formula
7. Can Heron's Formula be applied to all triangles, and what is the misconception students should avoid?
Heron’s Formula can be used for any triangle as long as all side lengths are known—including scalene, isosceles, and equilateral triangles. A common misconception is that it is only for triangles without a known height — in reality, it is a universal method for all triangles with known side lengths.
8. How does practicing with concept maps and summary charts help in revising Heron's Formula?
Creating concept maps and summary charts helps students visualize the sequence of steps, relate the formulas, and quickly recall all key points. This structured approach aids in fast revision and improves memory retention before exams.
9. What types of questions should be prioritized while revising Heron's Formula for exams?
Prioritize solving questions that ask you to:
- Find the area of a triangle given its three sides
- Apply Heron’s Formula to real-life and geometric problems
- Solve for the area of quadrilaterals split into triangles
- Compare different methods for area calculation
10. How can students use revision notes on Heron’s Formula to identify and avoid calculation errors in exams?
By regularly referencing revision notes, students can double-check each calculation step, especially when working with the semi-perimeter and square root. Notes highlight common errors, such as incorrect order of subtraction or misapplying the formula, enabling students to troubleshoot mistakes and calculate faster.