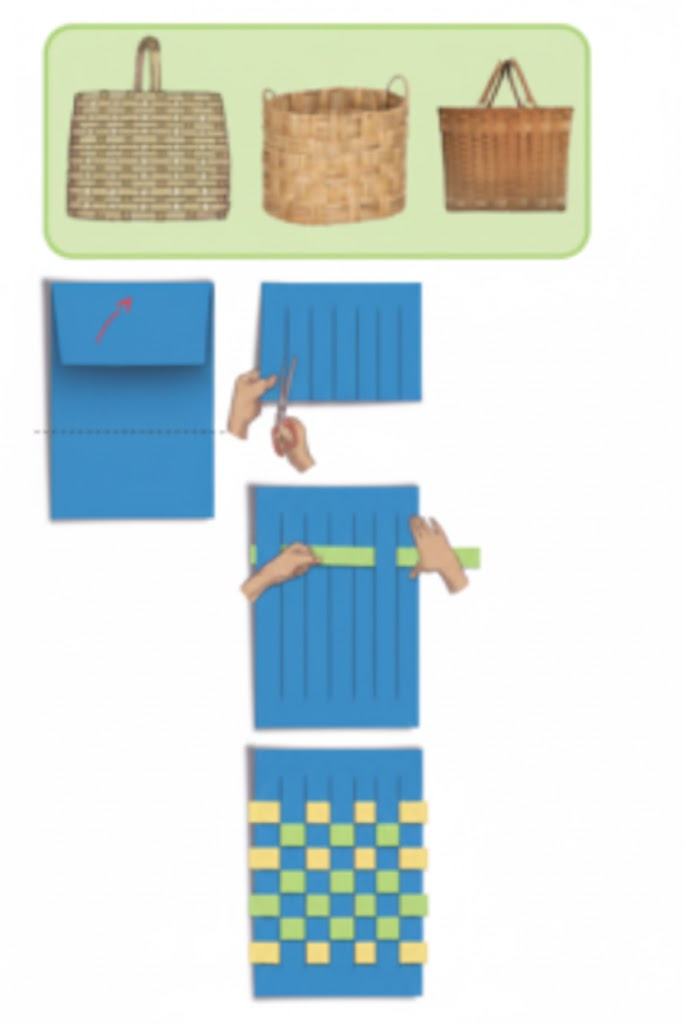
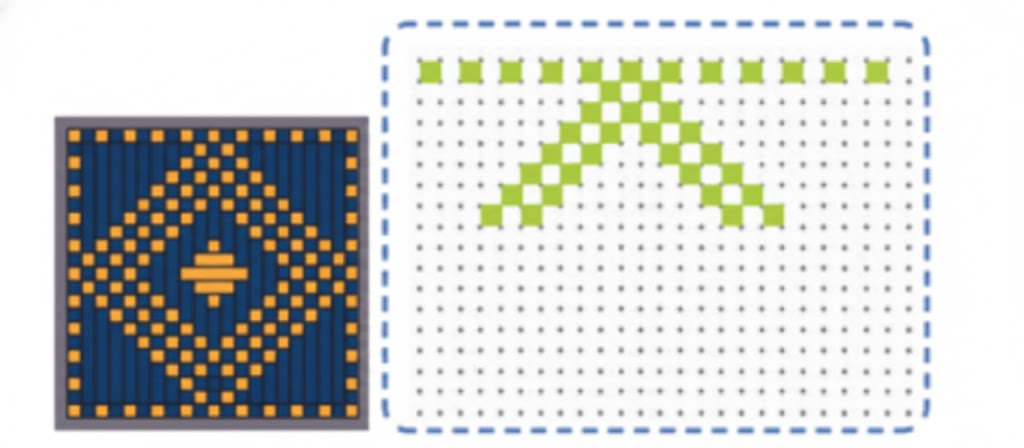
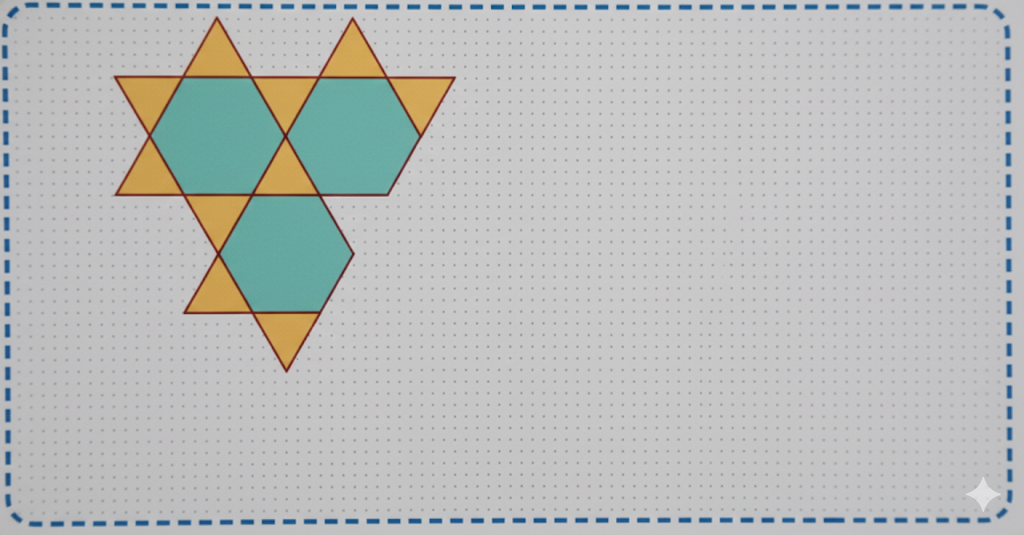
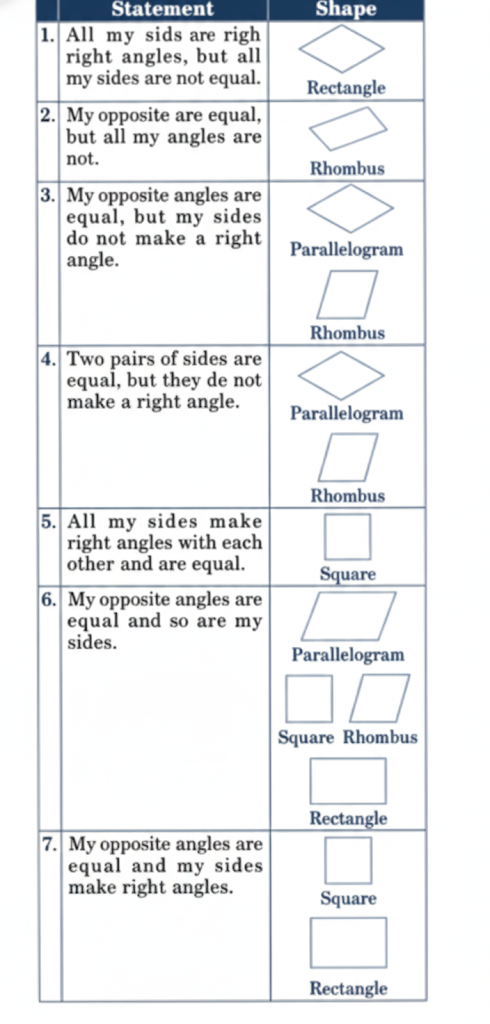
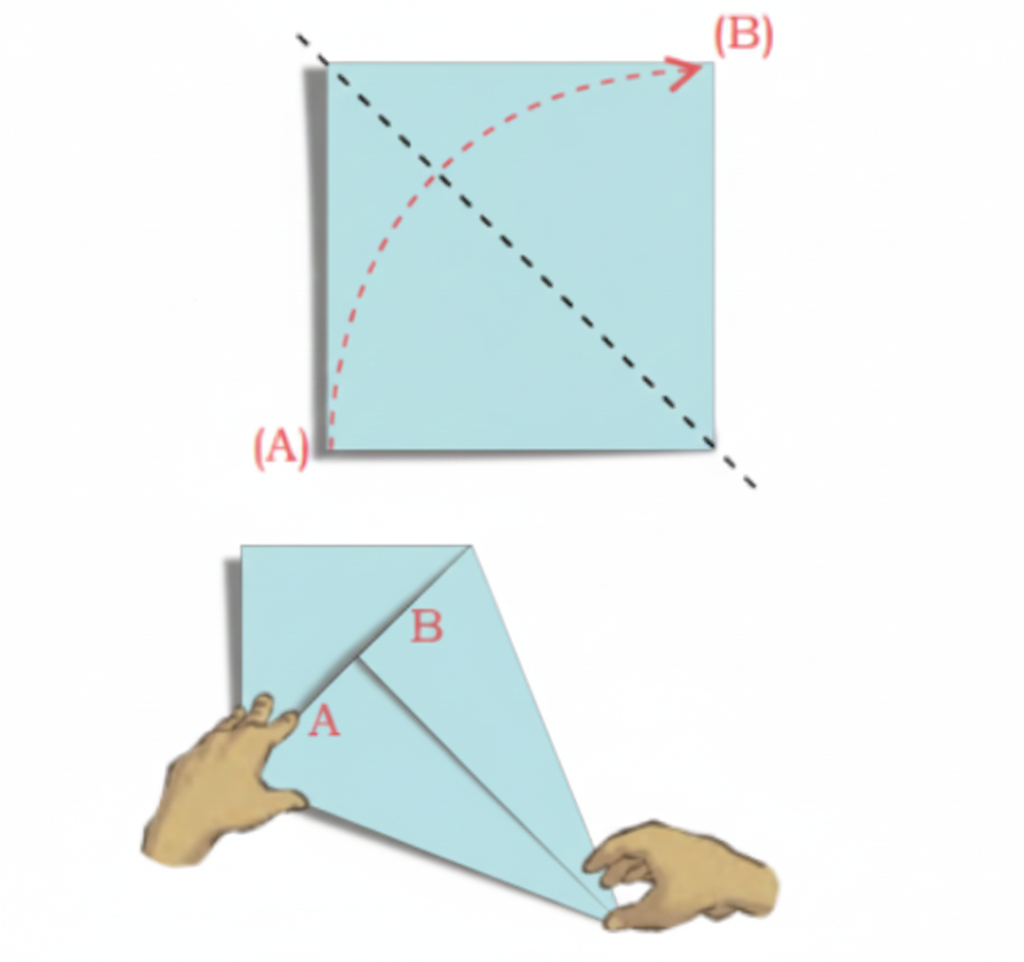
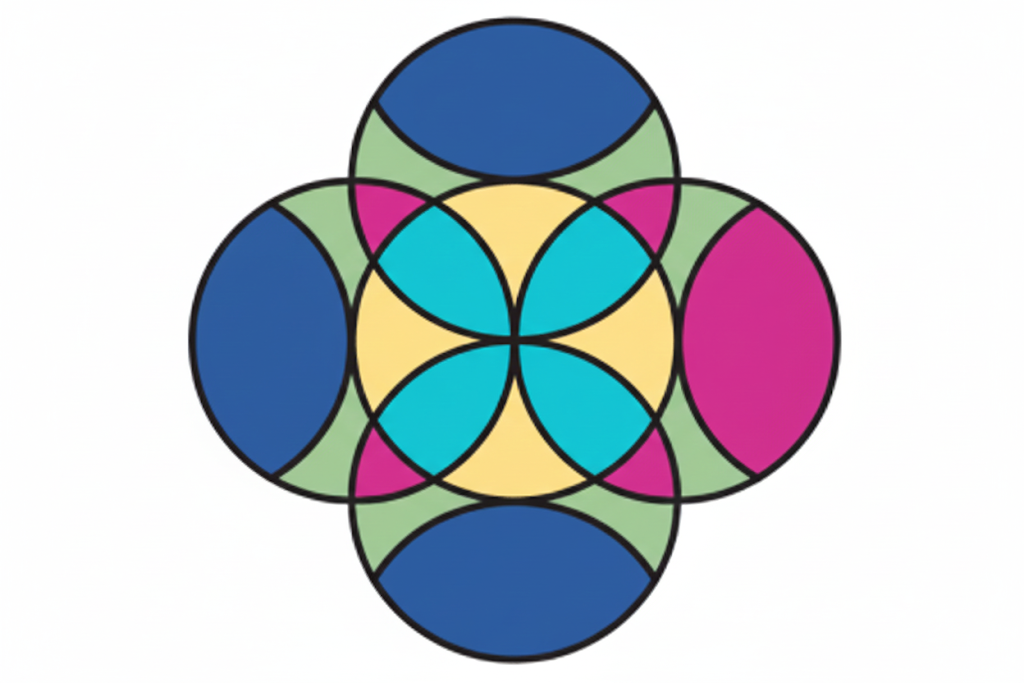
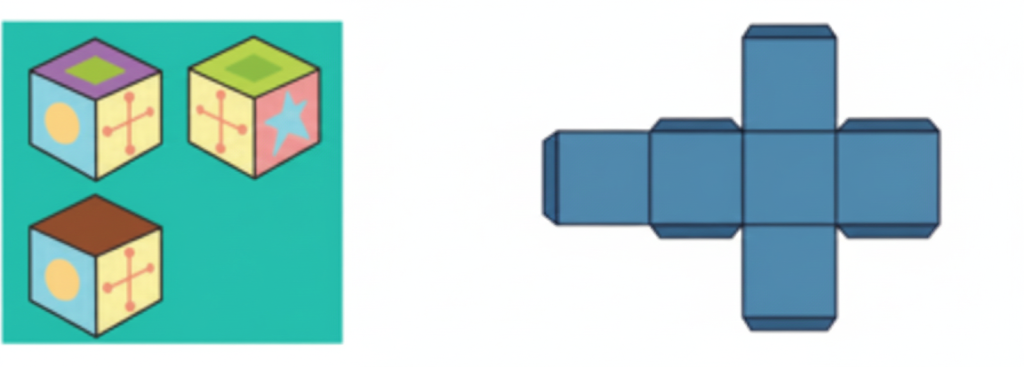
Exercise-wise Solutions for Class 5 Maths Chapter 7 Shapes and Patterns
FAQs on NCERT Solutions For Class 5 Maths Chapter 7 Shapes And Patterns - 2025-26
1. What is covered in NCERT Solutions for Class 5 Maths Mela Chapter 7 Shapes and Patterns?
NCERT Solutions for Class 5 Maths Chapter 7 provide comprehensive, stepwise answers to all exercises on shapes and patterns, following the CBSE 2025–26 syllabus. Key coverage includes:
- Clear explanations of different types of shapes and patterns
- Practice problems with diagrams and labeling
- Step-by-step solutions for intext and back exercises
- Important questions for exam preparation
- Tips to score full marks by following CBSE answer presentation
2. Are diagrams or definitions mandatory in answers for Class 5 Maths Chapter 7 Shapes and Patterns?
Yes, including diagrams and definitions is highly recommended to score full marks in Class 5 Maths Chapter 7. Follow these tips:
- Draw neat and well-labeled diagrams for questions on shapes or symmetry
- Write correct definitions for key terms like ‘pattern’, ‘symmetry’, and ‘geometry’ where asked
- Use appropriate mathematical language and labeling
3. How to write stepwise NCERT answers to score full marks?
To score full marks in NCERT Class 5 Maths Chapter 7:
- Start each answer with the relevant definition or concept
- Show every calculation and logical step clearly
- Include neat diagrams if applicable
- Highlight important keywords from the question
- Align your answer with the CBSE marking scheme
4. Which questions are likely from this chapter in school exams?
Important and likely questions from Chapter 7 include:
- Drawing and identifying symmetrical shapes
- Continuing or completing given patterns
- Classifying shapes based on properties (sides, corners, symmetry)
- Defining key terms like pattern, symmetry
- Drawing and labeling geometric shapes correctly
5. Where can I download the chapter’s solutions PDF?
You can download the free PDF of NCERT Solutions for Class 5 Maths Chapter 7 from trusted educational websites. Look for:
- Exercise-wise solutions in a single PDF
- Stepwise explanations and diagrams included
- CBSE 2025–26 syllabus relevance
6. Is shapes and patterns important for exams?
Yes, Chapter 7 Shapes and Patterns is very important for Class 5 exams. This chapter:
- Covers fundamental geometry concepts asked every year
- Includes high-scoring and practical visual questions
- Sharpens logical and observation skills needed for later classes
7. How to draw accurate geometry diagrams in exams?
To draw accurate geometry diagrams for Class 5 Maths Chapter 7:
- Use pencil and ruler for straight edges
- Label all sides, angles, and points clearly
- Keep diagrams neat and proportional
- Follow textbook examples for correct method
8. What are the most important topics from this chapter?
The most important topics in Class 5 Maths Chapter 7 Shapes and Patterns are:
- Symmetry and mirror images
- Types of shapes (polygons, circles, etc.)
- Pattern completion and continuation
- Identifying and drawing shapes
- Key definitions and properties
9. Do examiners award partial marks for correct steps even if the final answer is wrong?
Yes, CBSE examiners often give partial marks for correct steps in Maths Mela Chapter 7, even if the final answer is incorrect. To maximize your score:
- Show every working step clearly
- Include correct diagrams and labeling
- Use proper definitions and formulae
10. How to revise NCERT Class 5 Maths Chapter 7 Shapes and Patterns quickly before exams?
To revise Class 5 Maths Chapter 7 quickly:
- Go through short revision notes for shapes, patterns, and definitions
- Practice key diagrams and pattern questions
- Review important questions and sample papers
- Use 1-day or 3-day revision planners for last-minute prep