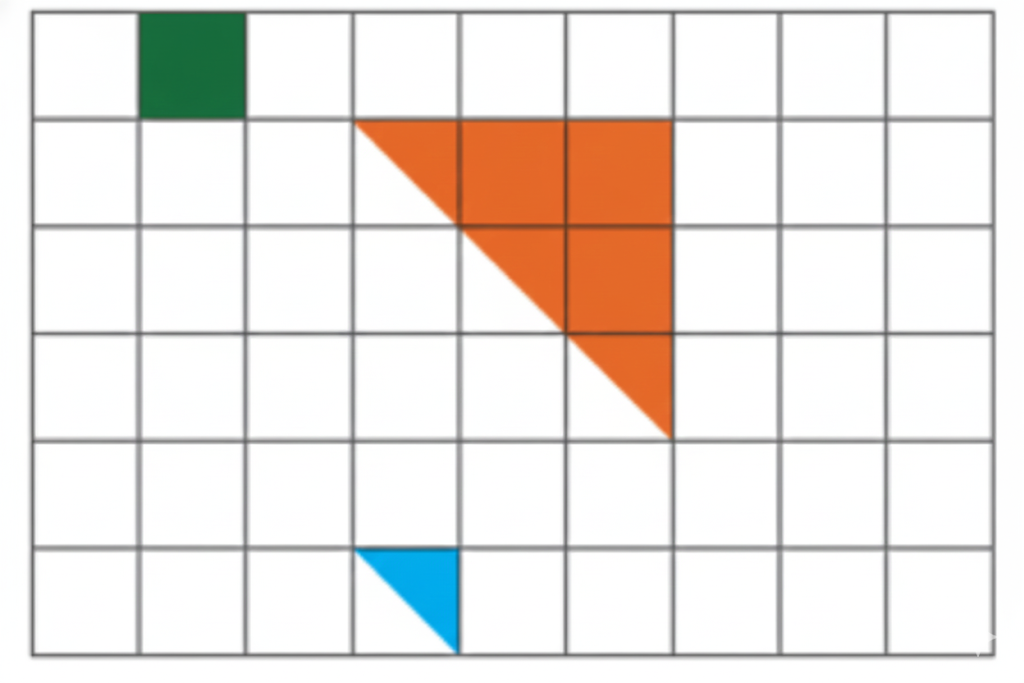
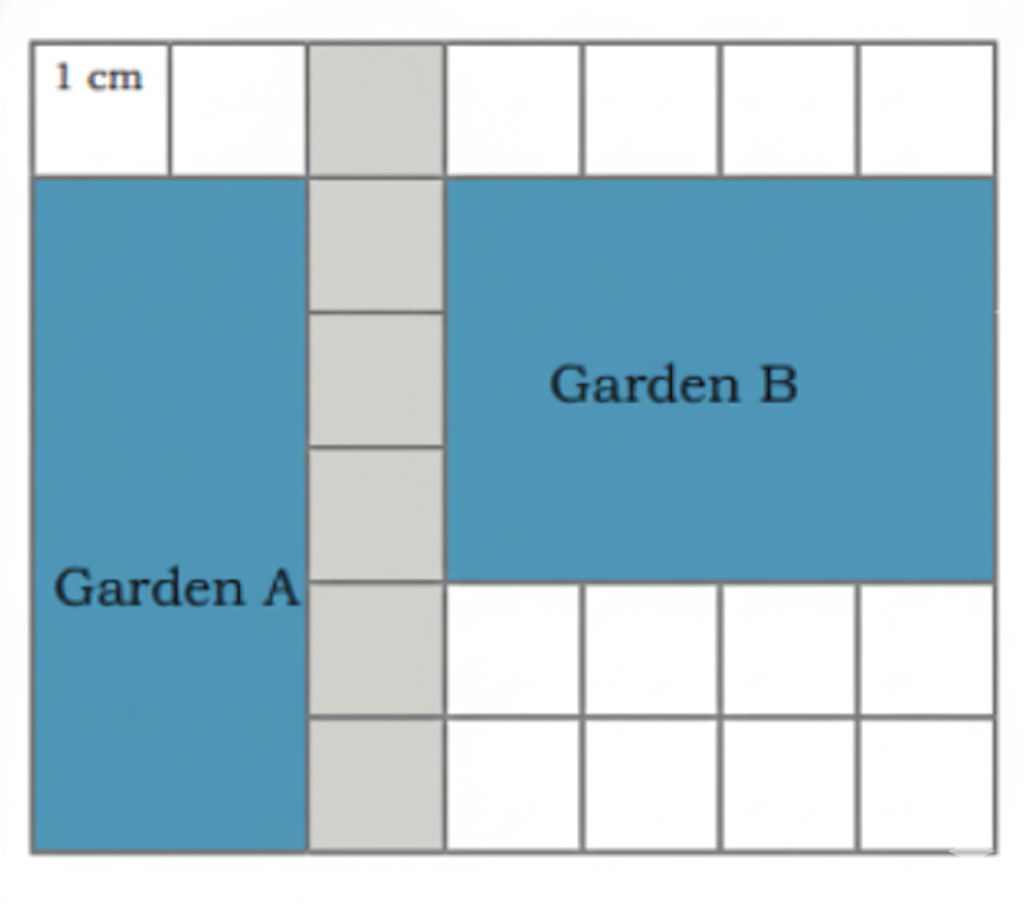
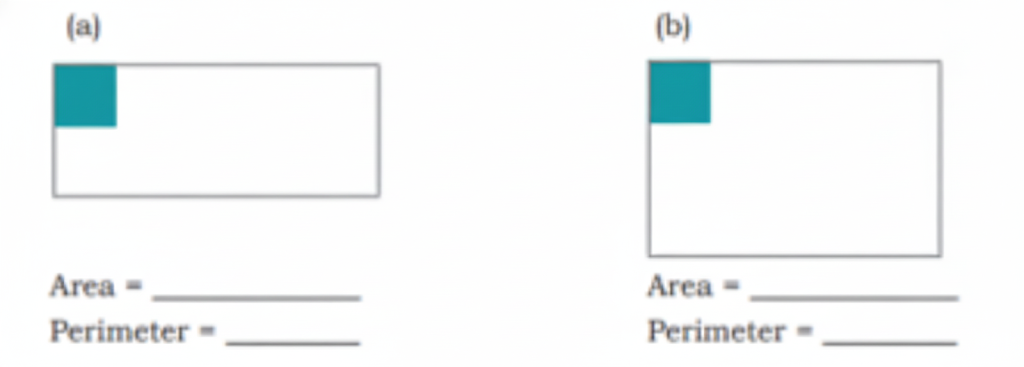
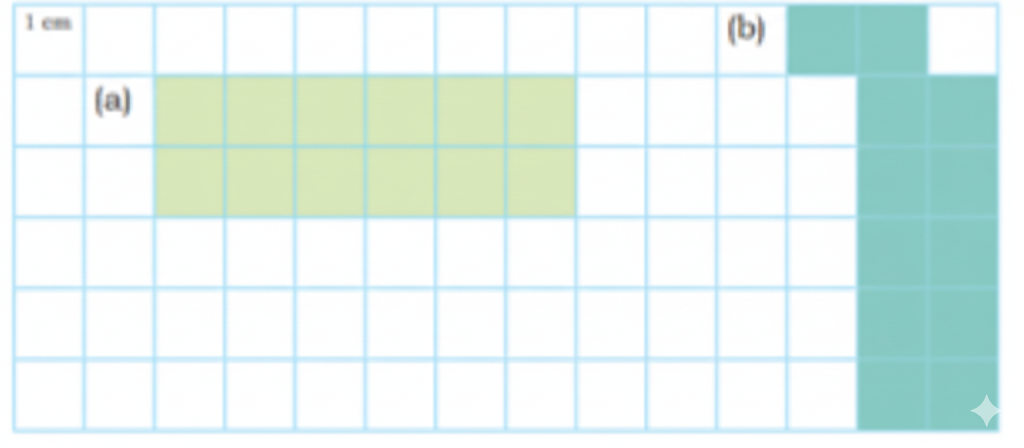
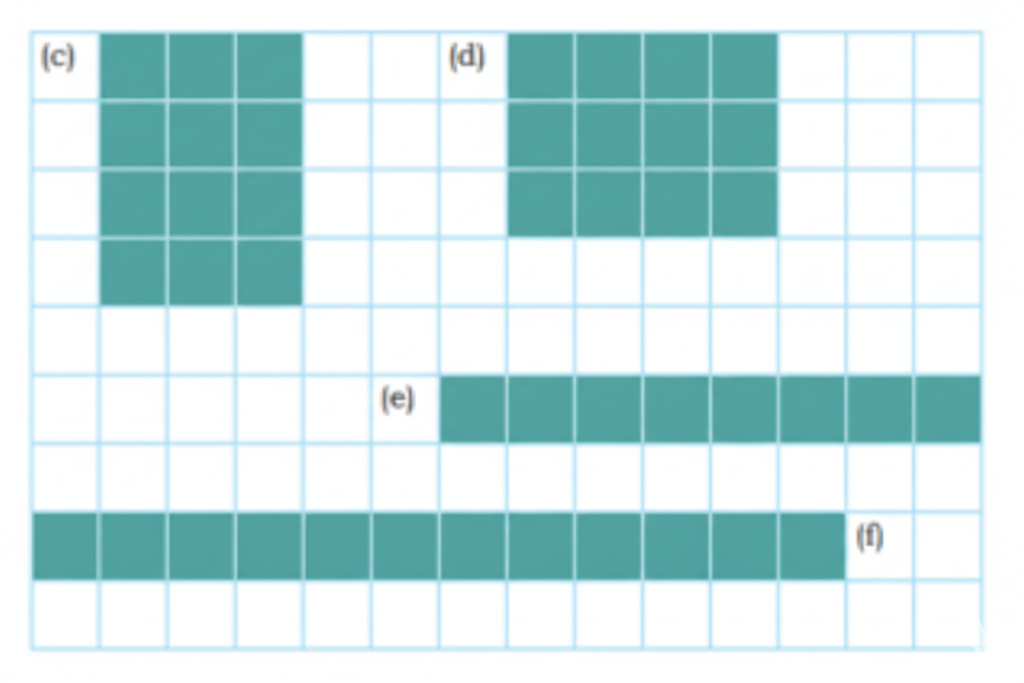
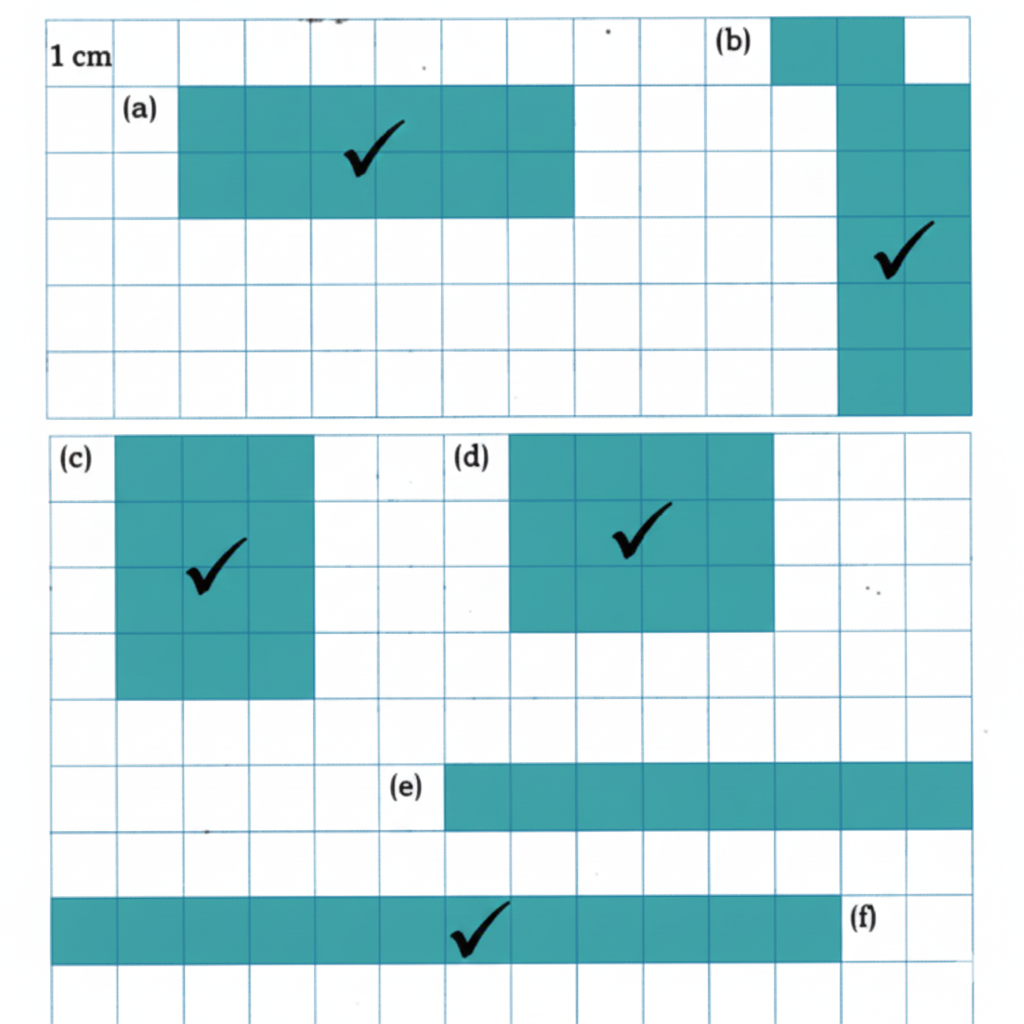
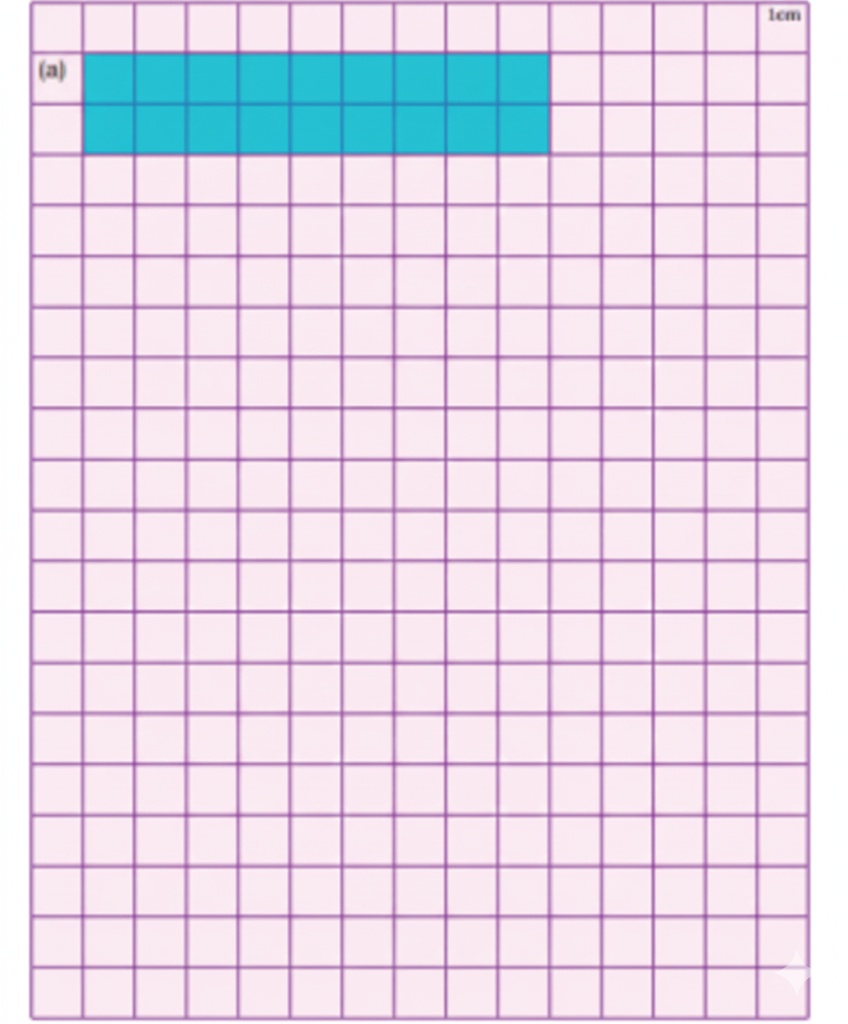
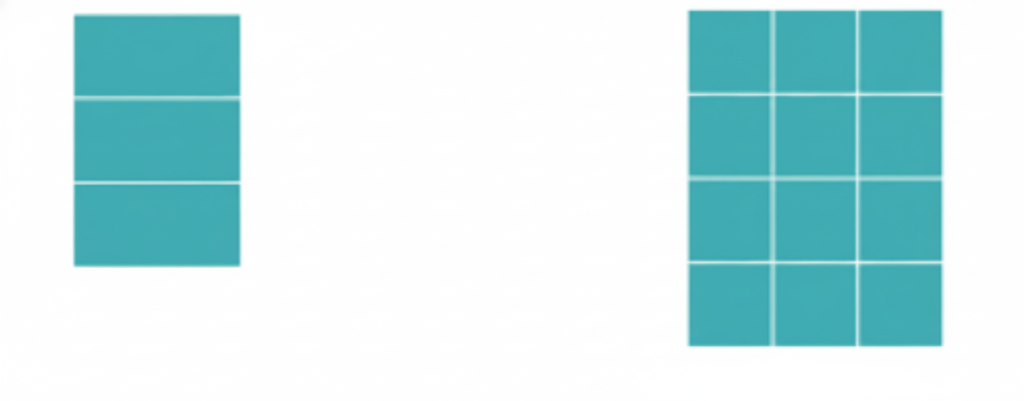How to Write Stepwise Answers and Score Full Marks in Grandmother’s Quilt?
NCERT Textbook Page 142
Let Us Do
Question 1.
Find the perimeter of the following shapes. All sides of the following shapes are equal.
Solution:
Perimeter of a shape
= Sum of lengths all sides Perimeter
= (4 + 4 + 4 + 4 + 4) cm
= 20 cm
Perimeter
= (5 + 5 + 5 + 5 + 5 + 5) cm
= 30 cm
Question 2.
Draw two rectangles each having the following perimeters.
(a) 26 cm
Solution:
(b) 18 cm
Solution:
NCERT Textbook Page 143
Preetha and Adrit’s grandmother is making a rug with square patches. The picture below shows the rug. How many patches have they used to make this?
Solution:
They used 90 square patches to make the rug.
Preetha and Adrit are trying to cover their table with different shapes. Preetha covered it with triangles and circles. Adrit covered with squares and rectangles.
They found that __________, __________ and __________ shapes cover the top of the table without gaps and overlaps. __________ shape leaves gaps.
__________ triangles cover Table 1.
__________ squares cover Table 3.
__________ rectangles cover Table 4
Solution:
They found that triangle, square and rectangle shapes cover the top of the table without gaps and overlaps. Circle shape leaves gaps.
20 triangles cover Table 1.
8 squares cover Table 3.
12 rectangles cover Table 4.
Do circles tile? Can we use them to cover a region?
The area of Table 1 is __________ triangle units.
The area of Table 3 is __________ square units.
The area of Table 4 is __________ rectangle units
Solution:
No, circles cannot tessellate because they leave gaps when placed together and cannot completely cover a surface.
The area of Table 1 is 20 triangular units.
The area of Table 3 is 8 square units.
The area of Table 4 is 12 rectangular units.
Now, try to cover the top of your table without gaps and overlaps with the following objects of same size.
(a) Notebooks
(b) Lunch boxes
(c) Pencil boxes
(d) Maths textbooks
Which of the above objects covered the region completely?
Solution:
Students should do it by themselves
NCERT Textbook Page 144
Let Us Do
Preetha is playing with tiles. She covers her desk with different shapes as shown below.
Look at the different tiles on her desk and answer how many of the following shapes will cover the desk.
(a) Green triangles
(b) Red triangles
(c) Blue squares
Solution:
(a) Two green triangles together make one square.
So, to cover 54 squares, we need:
2 × 54 = 108 green triangles.
Hence, 108 green triangles are required to cover the desk.
(b) One red triangle covers 4½ squares, which is equal to 9⁄2 squares.
Since the desk has 54 squares, the number of red triangles needed is:
54 ÷ (9⁄2) = (54 × 2) ÷ 9 = 12.
Therefore, 12 red triangles will cover the desk.
(c) One blue square covers exactly one square.
So, to cover 54 squares, we need 54 blue squares.
NCERT Textbook Pages 145-147
Let Us Do
Question 1.
Compare the areas of the two gardens given below on the square grid. Share your observations.
Area of Garden A = _____ cm square
Area of Garden B = _____ cm square
Solution:
From the picture, Garden A is made up of 10 unit squares, each with a side length of 1 cm.
So, the area of Garden A is 10 square centimetres.
Similarly, Garden B consists of 12 unit squares, each measuring 1 cm × 1 cm.
Hence, the area of Garden B is 12 square centimetres.
Since 12 cm² is greater than 10 cm², Garden B has a larger area than Garden A.
Question 2.
Trace your palm on the square grid given below and find the approximate area of your palm. Compare the area of your palm with your friend’s palm. Who has a bigger palm?
Solution:
Students should do it by themselves
Question 3.
Collect leaves of different kinds. Put them on a square grid and find their area.
(a) Name the leaf with the largest area.
(b) Name the leaf with the smallest area.
Solution:
Students should do it by themselves
Question 4.
The following mats are made of square patches of equal size. How many square patches will be required to cover each mat? Would both mats require an equal or different number of patches? Trace and cut out a small square of the size give below and find the area.
Solution:
Students should do it by themselves.
Trisha makes these two rectangles. She says, “I increased the area of my rectangle, and the perimeter increased. Do you think this is always true?
Solution:
To make the area of a rectangle larger, we must add unit squares along its length, breadth, or both. In every such case, the boundary of the rectangle becomes longer, and therefore, the perimeter also increases.
No, this statement is not always true.
Consider the following example:
Take a rectangle with length 8 cm and breadth 1 cm.
Its perimeter is:
2 × (8 + 1) = 18 cm
and its area is:
8 × 1 = 8 cm².
Now rearrange the rectangle so that the length is 5 cm and the breadth is 3 cm.
The new perimeter becomes:
2 × (5 + 3) = 16 cm,
while the area is:
5 × 3 = 15 cm².
Here, the area increases, but the perimeter decreases.
Therefore, it is not always true that increasing the area of a rectangle also increases its perimeter.
NCERT Textbook Pages 147-148
Let Us Explore
Question 1.
Tick the shapes with the same area. Find the perimeters of these shapes. What do you notice? Discuss.
Answers:
(a) Perimeter = 16 cm, Area = 12 cm²
(b) Perimeter = 18 cm, Area = 12 cm²
(c) Perimeter = 14 cm, Area = 12 cm²
(d) Perimeter = 14 cm, Area = 12 cm²
(e) Perimeter = 18 cm, Area = 8 cm²
(f) Perimeter = 26 cm, Area = 12 cm²
The shapes (a), (b), (c), (d), and (f) all have the same area.
This shows that figures can have equal areas but different perimeters.
Question 2.
Tick the shapes with the same perimeter. Find the areas of these shapes. What do you notice? Discuss.
Solution:
(a) Area = 18 cm², Perimeter = 22 cm
(b) Area = 18 cm², Perimeter = 18 cm
(c) Area = 18 cm², Perimeter = 22 cm
(d) Area = 18 cm², Perimeter = 26 cm
This shows that shapes with the same area can have different perimeters.
(Answer might be different)
Question 2.
Is the area of shape (a) less than the area of shape (b) given below? Discuss.
Preetha and Adrit’s grandmother is making another square patchwork. She arranges the patches as shown below. Can you guess how many patches she will need? How did you find it?
Solution:
The area of shape (a) is 9 unit squares.
The area of shape (b) is 6 full unit squares plus 6 half unit squares, which also equals 9 unit squares.
Therefore, shape (a) and shape (b) have the same area.
NCERT Textbook Pages 151-153
Let Us Do
Question 1.
Find the area of your classroom floor in square meters. Take the help of your teacher to measure the length and breadth of the floor. What is the perimeter of the classroom floor?
Solution:
Students should do it by themselves
Question 2.
Find the area and perimeter of the following shapes.
Solution:
(a) Length of the square = 6 cm
Area = Length × Length
= 6 × 6
= 36 square cm
Perimeter = 4 × Length
= 4 × 6
= 24 cm
(b) Length = 4 cm, Breadth = 7 cm
Area of rectangle = Length × Breadth
= 4 × 7
= 28 square cm Perimeter of rectangle
– = 2 × Length + 2 × Breadth
= 2 × 4 + 2 × 7
= 8 + 14
= 22 cm
(c) Length = 12 cm, Breadth = 4 cm
Area of rectangle = Length × Breadth
= 12 × 4
= 48 square cm
Perimeter of rectangle
= 2 × Length + 2 × Breadth
= 2 × 12 + 2 × 4
= 24 + 8
= 32 cm
(d) Length of the square = 3 cm
Area of square = Length × Length
= 3 × 3
= 9 square cm
Perimeter of square = 4 × length
= 4 × 3
= 12 cm
(e) Length = 6 cm, Breadth = 5 cm
Area of rectangle = Length × Breadth = 6 × 5
= 30 square cm
Perimeter of rectangle
= 2 × Length + 2 × Breadth
= 2 × 6 + 2 × 5
= 12 + 10
= 22 cm
Question 3.
Find the area and perimeter of the following objects. Use a scale or measuring tape to find the length and the breadth of each of the objects.
S. No. | Name of the objects | Area | Perimeter |
1. | Cover of the Notebook | ||
2. | Newspaper | ||
3. | Blackboard | ||
4. | Ludo board | ||
5. | |||
6. |
Solution:
Students should do it by themselves
Question 4.
Find the area of a rectangular field whose length is 42 m and breadth is 34 m.
Solution:
Length = 42 m, Breadth = 34 m
Area of rectangle = Length × Breadth
= 42 × 34
= 1428 square m
Therefore, the area of the rectangular field is 1428 square m.
Question 5.
The area of a rectangular garden is 64 square m and its length is 16 m. What is its breadth?
Solution:
Area = 64 square m, Length = 16m
Area of rectangle = Length × Breadth
64 = 16 × Breadth
Breadth = 64 + 16 = 4 m
Therefore, the breadth of rectangular garden is 4 m.
Question 6.
Find the area of the following figure with the dimensions as marked in the figure.
Solution:
Length = 32 cm,
Breadth = (6 + 12) cm = 18 cm
Area of the rectangular figure = Length × Breadth
= 32 × 18
= 576 square cm
Understanding Area and Perimeter in NCERT Class 5 Maths
The chapter Grandmother’s Quilt in NCERT Solutions Class 5 Maths Mela Chapter 11 (2025-26) helps students master the basics of area and perimeter. Practical questions, like measuring patches and tiling shapes, make concepts clear and fun to learn.
With step-by-step practice from this chapter, you’ll easily compare areas, calculate perimeters, and solve questions about rectangles, squares, and real-life objects. Consistent learning using NCERT Class 5 Maths Chapter 11 boosts confidence and scoring potential.
For best results, regularly revise formulas and try out the hands-on activities. Understanding patchwork, tiling, and measurement from the chapter will help you solve exam questions faster and develop a stronger foundation in Maths.
FAQs on Class 5 Maths Chapter 11 Grandmother’s Quilt – NCERT Solutions and Key Answers
1. What is the main concept in Grandmother’s Quilt?
The main concept of NCERT Solutions Class 5 Maths Mela Chapter 11 Grandmother’s Quilt is to understand mathematical patterns, shapes, and reasoning through creative and visual activities like quilt-making.
- Focuses on patterns and spatial reasoning
- Encourages visualization and creative thinking
- Teaches pattern identification and repetition through everyday examples
2. How to score full marks in Chapter 11 of Class 5 Maths?
To score full marks in Class 5 Maths Chapter 11, present your answers stepwise, use correct terms, and add neat diagrams where asked.
- Write clear, stepwise solutions using all keywords
- Draw and label diagrams accurately (if required)
- Revise definitions, formulae, and key patterns before the exam
- Check answers for neatness and completeness
- Practice with NCERT Solutions and attempt extra questions for confidence
3. Are diagrams needed in answers for Grandmother’s Quilt?
Yes, including diagrams in your answers is important, especially when describing or explaining patterns.
- Neat and labelled diagrams fetch extra marks
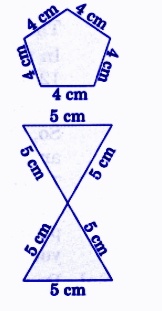
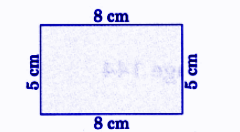
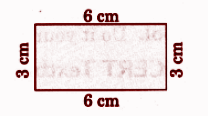
- Some questions specifically ask for pattern drawings, quilt designs, or shapes
- Always use a ruler and pencil for clear presentation
4. How do I present long answers to match CBSE marking?
Present long answers for CBSE Class 5 Maths Chapter 11 using a structured format:
- Start with a short introduction or definition of the concept
- List steps or observations using bullet points or numbers
- Add examples or diagrams if needed
- Underline or bold key terms and answers
- Summarize with a concluding statement
5. Where can I download the NCERT Solutions PDF for Class 5 Maths Chapter 11?
You can easily download the NCERT Solutions PDF for Class 5 Maths Chapter 11 Grandmother’s Quilt from trusted educational websites offering free study materials.
- Search for "Class 5 Maths Chapter 11 NCERT Solutions PDF free download"
- Look for platforms with up-to-date (2025–26) content
- Check if the PDF includes exercise-wise, stepwise answers and diagrams
- Save for offline study and revision
6. What are the most important topics from Chapter 11 Grandmother’s Quilt?
The most important topics in Class 5 Maths Mela Chapter 11 include:
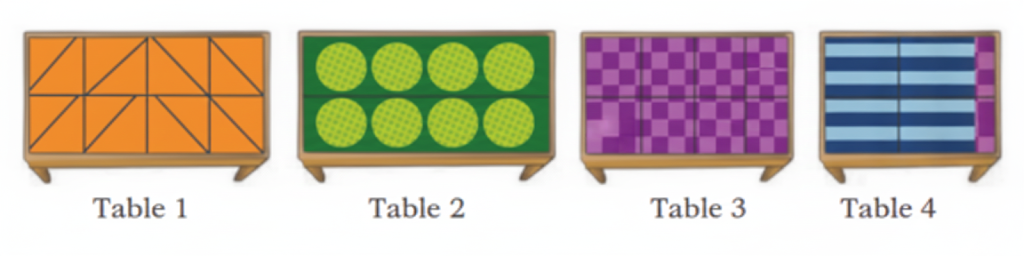
- Identifying and creating patterns
- Arranging and counting shapes in quilts
- Visualizing spatial arrangements
- Reasoning and completing pattern-based questions
- Drawing and labeling pattern diagrams correctly
7. How does practising stepwise NCERT Solutions help in Class 5 Maths exams?
Practising stepwise NCERT Solutions for Chapter 11 helps you:
- Understand concepts deeply and logically
- Learn the correct exam format for each question
- Avoid missing steps that can cost marks
- Boost confidence for difficult or creative reasoning questions
- Score higher by matching the CBSE marking scheme
8. What are the common mistakes to avoid in Class 5 Maths Chapter 11 answers?
To avoid losing marks, watch out for these common mistakes:
- Omitting steps or logic in your solutions
- Missing diagrams or drawing untidy patterns
- Forgetting to label shapes and explain reasoning
- Not following the exam structure (introduction, steps, conclusion)
- Leaving answers incomplete or not revising basic pattern rules
9. Is NCERT Solutions enough for Class 5 Maths exams?
NCERT Solutions for Class 5 Maths cover all the important topics and exercise questions as per the CBSE syllabus.
- They are sufficient for scoring well if thoroughly practiced
- Also revise with exemplar questions and sample papers for more practice
- Review diagrams, definitions, and marking schemes as given in NCERT
10. How can I revise Chapter 11 quickly before the test?
For fast revision of Chapter 11 Grandmother’s Quilt:
- Read key definitions and formulae first
- Review solved examples and stepwise answers from NCERT
- Practice drawing at least 2–3 pattern diagrams
- Attempt previous year and sample questions
- Go through a summary or quick revision notes
