NCERT Solutions for Class 10 Science Chapter 11 Electricity

Intext Exercise 1

1. What Does an Electric Circuit Mean?

Ans: An electric circuit can be defined as a continuous and closed path of an electric current.

The circuit consists of various electric devices.

2. Define the Unit of Current.

Ans: One ampere is constituted by the flow of one coulomb of charge per second. i.e.,

$$1A=\frac{1C}{1s}$$

3. Calculate the Number of Electrons Constituting One Coulomb of Charge.

Ans: Charge of $1$ electron $$=n\times e=1.6\times {10}^{-19}C$$

Assume $n$ electrons make one coulomb.  

So, 

$$n=\frac{1}{e}$$

$$\Rightarrow n=\frac{1}{(1.6\times {10}^{-19})}$$

$$\Rightarrow n=6.25\times {10}^{18}$$

Therefore, $\text{1}$ coulomb of charge constitutes $$\text{6}\text{.25}\times \text{1}{\text{0}}^{\text{18}}$$ electrons.

Intext Exercise 2 

1. Name a Device That Helps To Maintain a Potential Difference Across a Conductor.

Ans: Any device like a cell or a battery can maintain potential difference in a circuit and across a conductor. 

2. What Is Meant by Saying That the Potential Difference Between Two Points is $$\text{1 V}$$?

Ans:  It means that$$\text{1 J}$$ of work is done in moving $$\text{1 C}$$ charge from one point to the other.  

3. How Much Energy Is Given to Each Coulomb of Charge Through a $$\text{6 V}$$ battery? 

Ans: We can find the energy given to a charge by finding the work it does in the circuit. 

Work done in circuit is given by, 

Work Done = Potential Difference × Charge

Where, 

Charge $$=1C$$

Potential difference $$=6V$$

Work Done $$=6\times 1=6J$$

Therefore, $\text{6J}$ of energy is given to each coulomb of charge passing through a battery of $$\text{6 V}$$.  

Intext Exercise 3

1. On What Factors Does the Resistance of a Conductor Depend?

Ans: The resistance of a conductor depends upon the following factors: 

Length of the conductor $$\left(\text{l}\right)$$.

Cross-sectional area of the conductor $$\left(\text{A}\right)$$.

Nature of Material of the conductor $$\left(\rho \right)$$.

Temperature of the conductor $$\left(T\right)$$.

2. Will Current Flow More Easily Through a Thick Wire or a Thin Wire of the Same Material, When Connected to the Same Source? Why?

Ans: The relation between resistance and the area of cross section can be given as: $\text{R}\propto \frac{\text{1}}{\text{A}}$.

Resistance is inversely proportional to the area of cross-section of the wire. As the resistance decreases, the current increases.  

Thicker the wire, less current will pass through it whereas thinner the wire, more current will pass.  

3. Let the Resistance of an Electrical Component Remain Constant While the Potential Difference Across the Two Ends of the Component Decreases to Half of Its Former Value. What Change Will Occur in the Current Through It?

Ans:  The change in the current flowing through the component is given by Ohm’s law as,

$$V=IR$$

$\Rightarrow I=\frac{V}{R}$

Where, 

$$\text{R}$$ is Resistance of the electrical component. 

$$V$$ is the Potential Difference.

$$\text{I}$$ is the Current  

If the potential difference is halved keeping $$\text{R}$$the same, 

$I_2=\frac{V_2}{R}$

Where $V_2=\frac{V}{2}$

$\Rightarrow I_2=\frac{V}{2R}$

But we know that $I=\frac{V}{R}$

$\Rightarrow I_2=\frac{I}{2}$

That is, the current gets halved.  

4. Why are Coils of Electric Toasters and Electric Irons Made of an Alloy Rather Than a Pure Metal?

Ans: The alloys are made such that their resistivity is higher than metals. And they don’t melt at high temperatures.  

5. Use the Data in Table To Answer the Following:

Table: Electrical resistivity of some substances at $$\text{20 }{}^{\circ }\text{ C}$$

a) Which Among Iron and Mercury is a Better Conductor?

Ans: Resistivity of iron$=10.0\times {10}^{-8}\mathrm{\Omega }m$ 

Resistivity of mercury$=94.0\times {10}^{-8}\mathrm{\Omega }m$  

Resistivity of mercury is more than that of iron. So, iron is a better conductor than mercury because resistivity is inversely proportional to conductivity.

b) Which Material is the Best Conductor?

Ans: Metal with least resistivity is the best conductor. In the above 

question, according to the table, Silver is the best conductor.  

Intext Exercise 4 

1. Draw a Schematic Diagram of a Circuit Consisting of a Battery of Three Cells of $$\text{2 V}$$ each, a $$\text{5 }\mathrm{\Omega }$$ resistor, an $$\text{8 }\mathrm{\Omega }$$ resistor, and a $$\text{12 }\mathrm{\Omega }$$ resistor, and a Plug Key, All Connected in Series.

Ans: The following circuit diagram shows three resistors of resistances $\text{5}\mathrm{\Omega }$, $$\text{8 }\mathrm{\Omega }$$ and $$\text{12 }\mathrm{\Omega }$$ respectively connected in series with a battery of potential $$\text{6 V}$$.                                                                                                                                                                                                                    

2. Redraw the Circuit of Question $1$, Putting in an Ammeter To Measure the Current Through the Resistors and a Voltmeter To Measure Potential Difference Across the $$12\mathrm{\Omega }$$ resistor. What Would Be the Readings in the Ammeter and the Voltmeter?

Ans: An ammeter should be connected in series with the resistors in the circuit, to measure the current flowing through the resistors.

To measure the potential difference across the$$12\mathrm{\Omega }$$ resistor, a voltmeter should be connected parallel across the$$12\mathrm{\Omega }$$ resistor, as shown in the figure below.

Let’s find the total current in the circuit. That should be the same as the current through each resistor and the ammeter.  

$$R_{eq}=R1+R2+R3$$

$$\Rightarrow R_{eq}=5+8+12$$

$$\Rightarrow R_{eq}=25\mathrm{\Omega }$$

Hence, $$I_{eq}=\frac{V}{R_{eq}}$$

$$\Rightarrow I_{eq}=\frac{6}{25}=0.24A$$

Thus, the ammeter will read $$0.24A$$.

Voltage across $$R_3=V_3$$

$$\Rightarrow V_3=I_{eq}\times R_3$$

$$\Rightarrow V_3=0.24\times 12$$

$$\Rightarrow V_3=2.88$$

Thus, the voltmeter will read $$2.88V$$.

Intext Exercise 5 

1. Judge the Equivalent Resistance When the Following Are Connected in Parallel: 

a) $$1\mathrm{\Omega }$$ and $${10}^6\mathrm{\Omega }$$ 

Ans: In parallel connection, we can state that, equivalent resistance is lesser than the least resistance. 

So, in both the cases, the resistance should be less than $$1\mathrm{\Omega }$$. Verification of these statements can be done as below:

When $$1\mathrm{\Omega }$$and $${10}^6\mathrm{\Omega }$$are connected in parallel:

Let $R$ be the equivalent resistance.

$\frac{1}{R}=\frac{1}{1}+\frac{1}{{10}^6}$

$\Rightarrow R=\frac{{10}^6}{{10}^6+1}\approx \frac{{10}^6}{{10}^6}$

$\Rightarrow R=1\mathrm{\Omega }$

Therefore, equivalent resistance is less than $$1\mathrm{\Omega }$$.

b) $$1\mathrm{\Omega },{10}^3\mathrm{\Omega }$$ and $${10}^6\mathrm{\Omega }.$$

Ans: When $$1\mathrm{\Omega },{10}^3\mathrm{\Omega }$$ and $${10}^6\mathrm{\Omega }.$$are connected in parallel: 

Let $R$ be the equivalent resistance. 

$\frac{1}{R}=\frac{1}{1}+\frac{1}{{10}^3}+\frac{1}{{10}^6}=\frac{{10}^6+{10}^3+1}{{10}^6}$

$\Rightarrow R=\frac{1000000}{1000001}=0.999\mathrm{\Omega }$

Therefore, equivalent resistance $$=0.999\mathrm{\Omega }$$, which is less than$$1\mathrm{\Omega }$$.

2. An Electric Lamp of  $$\text{100 }\mathrm{\Omega }$$, a Toaster of Resistance $$\text{50 }\mathrm{\Omega }$$, and a Water Filter of Resistance $$\text{500 }\mathrm{\Omega }$$ are Connected in Parallel to a $$\text{220 V}$$Source. What is the Resistance of an Electric Iron Connected to the Same Source That Takes as Much Current as all Three Appliances, and What is the Current Through it? 

Ans: Given that,

Resistance of electric lamp, $${\text{R}}_{\text{1}}\text{= 100 }\mathrm{\Omega }$$

Resistance of toaster, $${\text{R}}_{\text{2}}\text{= 50 }\mathrm{\Omega }$$

Resistance of water filter, $${\text{R}}_{\text{3}}\text{= 500 }\mathrm{\Omega }$$

Voltage of the source, $$\text{V = 220 V }$$

These are connected in parallel, as shown in the following figure. 

Let $R$ be the equivalent resistance of the circuit. 

$\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}=\frac{1}{100}+\frac{1}{50}+\frac{1}{500}=\frac{5+10+1}{500}=\frac{16}{500}$

$\Rightarrow R=\frac{500}{16}\mathrm{\Omega }$

According to Ohm’s law,

$$\text{V = IR }$$

$\Rightarrow I=\frac{V}{R}$

Where, 

Current flowing through the circuit $$\text{= I }$$

$\Rightarrow I=\frac{220}{\frac{500}{16}}=\frac{200\times 16}{500}=6.4A$

Hence, $$\text{6}\text{.4 A}$$of current is drawn by all the three given appliances. 

Therefore, current drawn by an electric iron connected to the same source of potential$$\text{(220 V)}$$ $$\text{=6}\text{.4 A }$$

Let  $\text{R }{}^{\prime }$ be the resistance of the electric iron. According to Ohm’s law, 

$$\text{V = I{R}'}$$

$\Rightarrow R^{\prime }=\frac{V}{I}=\frac{220}{6.4}=34.375\mathrm{\Omega }$

Therefore, the resistance of the electric iron is $$\text{34}\text{.375 }\mathrm{\Omega }$$ and the current flowing through it is $$\text{6}\text{.4A}\text{. }$$

3. What Are the Advantages of Connecting Electrical Devices in Parallel With the Battery Instead of Connecting Them in Series?

Ans: All the devices receive the same voltage in parallel connection. 

Failure of one device results does not disrupt the complete circuit.

Overall resistance is reduced.  

4. How Can Three Resistors of Resistances $$\text{2 }\mathrm{\Omega }\text{ , 3 }\mathrm{\Omega }$$ and $$\text{6 }\mathrm{\Omega }$$ be Connected to Give a Total Resistance of 

a) $$\text{4 }\mathrm{\Omega }$$? 

Ans: There are three resistors of resistances $$\text{2 }\mathrm{\Omega }\text{ , 3 }\mathrm{\Omega }$$ and $$\text{6 }\mathrm{\Omega }$$ respectively.

Consider the circuit below: 

Here, $$\text{6 }\mathrm{\Omega }$$ and $$\text{3 }\mathrm{\Omega }$$

 resistors are connected in parallel. 

Therefore, their equivalent resistance will be given by 

$\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}$

$\Rightarrow R=\frac{1}{\frac{1}{6}+\frac{1}{3}}=\frac{6\times 3}{6+3}=2\mathrm{\Omega }$

This combination is connected to a $$\text{2 }\mathrm{\Omega }$$ resistor in series. 

Therefore, equivalent resistance of the circuit $$=2\mathrm{\Omega }+2\mathrm{\Omega }=4\mathrm{\Omega }$$

Hence, the total resistance of the circuit is $$\text{4 }\mathrm{\Omega }$$. 

b) $$\text{ 1 }\mathrm{\Omega }$$

Ans: The following circuit diagram shows the connection of the three resistors. 

All the resistors are connected in parallel. Therefore, their equivalent resistance will be given as 

$R=\frac{1}{\frac{1}{2}+\frac{1}{3}+\frac{1}{6}}=\frac{1}{\frac{3+2+1}{6}}=\frac{6}{6}=1\mathrm{\Omega }$

Therefore, the total resistance of the circuit is $$\text{1 }\mathrm{\Omega }\text{. }$$

5. What is 

a) The Highest Total Resistance that can be Secured by Combinations of Four Coils of Resistance $$\text{4 }\mathrm{\Omega }\text{ , 8 }\mathrm{\Omega }\text{ , 12 }\mathrm{\Omega }\text{ , 24 }\mathrm{\Omega }$$? 

Ans: There are four coils of resistances $$\text{4 }\mathrm{\Omega }\text{ , 8 }\mathrm{\Omega }\text{ , 12 }\mathrm{\Omega }\text{ , 24 }\mathrm{\Omega }$$ respectively. 

To get highest resistance we must connect these resistances in series. Their equivalent resistance is given by the sum $$4+8+12+24=48\mathrm{\Omega }$$.

b) The Lowest Total Resistance that can be Secured by Combinations of Four Coils of Resistance $$\text{4 }\mathrm{\Omega }\text{ , 8 }\mathrm{\Omega }\text{ , 12 }\mathrm{\Omega }\text{ , 24 }\mathrm{\Omega }$$? 

Ans: For lowest resistance connect them in parallel. 

Here, $${\text{R}}_{eq}$$is given by 

$R_{eq}=\frac{1}{\frac{1}{4}+\frac{1}{8}+\frac{1}{12}+\frac{1}{24}}=\frac{1}{\frac{6+3+2+1}{24}}=\frac{24}{12}=2\mathrm{\Omega }$

Therefore,$$\text{2 }\mathrm{\Omega }$$ is the lowest possible equivalent resistance.

Intext Exercise 6 

1. Why Does the Cord of an Electric Heater Not Glow While the Heating Element Does?

Ans: Heat produced in a system is proportional to its resistance. 

The resistance of the heating element is more; so more heat is produced and so it glows. 

Also, the resistance of wire is less; so, the heat produced is also less. Hence, the wire does not glow but the heating element does.

2. Compute the Heat Generated While Transferring $$\text{96000}$$coulomb of Charge in One Hour Through a Potential Difference of $$\text{50 V}$$. 

Ans: The amount of heat $$\left(\text{H}\right)$$produced is given by the Joule’s law of heating as

$$H=VIt$$

Where, 

Voltage, $$V=50V$$

Time, $$t=1h=1\times 60\times 60s$$

$H=V.I.t$

$\Rightarrow H=V\cdot \frac{q}{t}\cdot t$

$\Rightarrow H=V\cdot q$

$\Rightarrow H=50\times 96000$

$\Rightarrow H=4.8\times {10}^{6}J$

Thus, heat produced while transferring the charge is $H=4.8\times {10}^{6}J$.

3. An Electric Iron of Resistance $$\text{20 }\mathrm{\Omega }$$ Takes a Current of $$\text{5 A}$$. Calculate the Heat Developed in $$\text{30 s}$$. 

Ans: The amount of  $$\left(\text{H}\right)$$heat produced is given by the Joule’s law of heating as $$H=VIt=I^{2}Rt$$.

Where, 

Current, $$\text{I = 5 A }$$

Time, $$\text{t = 30 s }$$

Resistance $$\text{R = 20}\mathrm{\Omega }$$

$H=I^{2}Rt$

$\Rightarrow H=5^2\times 20\times 30$

$\Rightarrow H=1.5\times {10}^{4}J$

Therefore, the amount of heat developed in the electric iron is $H=1.5\times {10}^{4}J$.

Intext Exercise 7

1. What Determines the Rate at Which Energy is Delivered by a Current?

Ans: The rate at which energy is delivered by a current or consumed by the appliance is the power of the appliance.

2. An Electric Motor Takes $$\text{5 A}$$ from a $$\text{220V}$$ line. Determine the Power of the Motor and the Energy Consumed in $\text{2}$ hrs. 

Ans: Power $$\left(\text{P}\right)$$is given by the expression $$\text{P}=\text{VI }$$.

Where, 

Voltage, $$\text{V= 220 V }$$

Current, $$\text{I = 5 A }$$

$$\text{P = 220 }\times \text{ 5 = 1100 W }$$

Energy consumed by the motor$=P\times t$

Where, 

Time, $$t=2h=2\times 60\times 60=7200s$$

$$\Rightarrow P=1100\times 7200$$

Therefore, the power of the motor $$=\text{1100 W }$$

Energy consumed by the motor $=\text{7}\text{.92 }\times \text{ 1}{\text{0}}^{\text{6}}\text{J}$.

NCERT Exercise  

1. A Piece of Wire of Resistance $\text{R}$ is Cut into Five Equal Parts. These parts are then Connected in Parallel. If the Equivalent Resistance of this Combination is $$\text{R }{}^{\prime }$$, then the Ratio $$\text{R/R }{}^{\prime }$$ is

a. $\frac{\text{1}}{\text{25}}$

b. $\frac{\text{1}}{\text{5}}$

c. $\text{5}$

d. $\text{25}$

Ans: Relation between resistance and current is $R\propto I$.

If the wire is cut into five equal parts, the resistance of each part $$=\frac{R}{5}$$.

All the five parts are connected in parallel. Hence, equivalent resistance $$\left(\text{{R}'}\right)$$is given as

$\frac{1}{R^{\prime }}=\frac{5}{R}+\frac{5}{R}+\frac{5}{R}+\frac{5}{R}+\frac{5}{R}=\frac{5+5+5+5+5}{R}=\frac{25}{R}$

$\Rightarrow \frac{R}{R^{\prime }}=25$

Therefore, the ratio $$\frac{R}{R^{\prime }}$$ is $25$. 

2. Which of the Following Does Not Represent Electric Power in a Circuit?

a. $${\text{I}}^{\text{2}}\text{R}$$ 

b. $$\text{I}{\text{R}}^{\text{2}}$$

c. $VI$ 

d. $\frac{{\text{V}}^{\text{2}}}{\text{R}}$

Ans: The correct option is (b). 

Electrical power is given by the expression, $$\mathrm{P}=VI$$…(i) 

According to Ohm’s law, $$\text{V = IR}$$ … (ii) 

Clearly, apart from ($\text{b}$), all the other equations can be converted to $$\text{V I }$$.

3. An Electric Bulb is Rated $$\text{220 V}$$ and $$\text{100 W}$$. When it is operated on $$\text{110 V}$$,the Power Consumed Will be 

a). $$\text{100 W }$$

b). $$\text{75 W }$$

c). $$\text{50 W }$$

d). $$\text{25 W}$$

Ans: The correct answer is option (d).

Energy consumed by an appliance is given by the expression, 

$$\text{P = VI = }\frac{{\text{V}}^{\text{2}}}{\text{R}}$$

The resistance of the bulb remains constant if the supply voltage is reduced to $$\text{110 V}$$. So, resistance should be found first.  

$\Rightarrow R=\frac{V^2}{P}$

Given $$\text{P = 100 W }$$;

$$\text{V = 220 V }$$;

$$\Rightarrow R=\frac{{\left(220\right)}^2}{100}=484\mathrm{\Omega }$$

Now if the bulb is operated on $$\text{110 V}$$, then the energy consumed by it is given by the expression for power as

$\Rightarrow P^{\prime }=\frac{{\left(V^{\prime }\right)}^2}{R}=\frac{{\left(110\right)}^2}{484}=25W$.

4. Two Conducting Wires of the Same Material and of Equal Lengths and Equal Diameters Are First Connected in Series and Then Parallel in a Circuit Across the Same Potential Difference. The Ratio of Heat Produced in Series and Parallel Combinations Would be 

a). $$\text{1:2 }$$

b). $$\text{2:1 }$$

c). $$\text{1:4 }$$

d). $$\text{4:1 }$$

Ans: The ratio of heat produced in series and parallel combinations would be $$\text{1:4 }$$and the correct answer is option (c).

For the same $\text{V}$ and $\text{t}$; ratio of heat produced in series $${\text{H}}_S$$ to heat produced in parallel $${\text{H}}_P$$ is given by, 

$\frac{H_S}{H_P}=\frac{\frac{V^2}{R_S}t}{\frac{V^2}{R_P}t}=\frac{R_P}{R_S}$ 

Now, $$R_s=R+R=2R$$;

$\Rightarrow R_p=\frac{1}{\frac{1}{R}+\frac{1}{R}}=\frac{R}{2}$

Hence, ratio: 

$\frac{H_S}{H_P}=\frac{\frac{R}{2}}{2R}=\frac{1}{4}$

Therefore, the ratio of heat produced in series and parallel combinations is $$\text{1:4}\text{. }$$

5. How is a Voltmeter Connected in the Circuit To Measure the Potential Difference Between Two Points?

Ans: The voltmeter should be connected in parallel to measure the potential difference between two points. 

This is because the voltage across the circuit in parallel can be determined by the voltmeter. 

On the other hand, for a series circuit, voltmeters cannot be used. Instead, an ammeter is used in a series circuit.

6. A Copper wire has Diameter $$\text{0}\text{.5 mm}$$and resistivity of $$\text{1}\text{.6 }\times \text{ 1}{\text{0}}^{\text{-8}}\mathrm{\Omega }\text{ m}\text{.}$$ What Will be the Length of this Wire to Make its Resistance $$\text{10 }\mathrm{\Omega }$$? How Much Does the Resistance Change if the Diameter is Doubled? 

Ans: Resistance $$\left(\text{R}\right)$$of a copper wire of length $$lm$$and cross-section $$A{m}^2$$ is given by the expression, 

$R=\rho \frac{l}{A}$

Where,

Resistivity of copper, $$\rho =1.6\times {10}^{-8}\mathrm{\Omega }m$$

Area of cross-section of the wire, $$A=\pi {\left(\frac{Diameter}{2}\right)}^2$$

Diameter$$\text{= 0}\text{.5 mm = 0}\text{.0005 m }$$

Resistance, $$\text{R= 10 }\mathrm{\Omega }$$

Hence, length of the wire,$l=\frac{RA}{\rho }=\frac{10\times 3.14\times {\left(\frac{0.005}{2}\right)}^2}{1.6\times {10}^{-8}}=\frac{10\times 3.14\times 25}{4\times 1.6}=122.65m$

If the diameter of the wire is doubled, new diameter$$D^{\prime }=2\times 0.5=1mm=0.001m$$

Now, let’s find the new resistance with a new diameter (twice the old one). i.e., 

$$D^{\prime }=2D$$

$$\Rightarrow A^{\prime }=p\left(D^{\prime }/2\right)2=4A$$

Now new resistance will also be reduced 4 times.  

$$\text{{R}' = R/4 }$$

$$\Rightarrow \text{{R}'}=\text{10/4}=\text{2}\text{.5 }\mathrm{\Omega }$$

Therefore, the length of the wire is $$\text{122}\text{.65 m}$$ and the new resistance is $$\text{2}\text{.5 }\mathrm{\Omega }\text{. }$$

7. The Values of Current $\text{I}$ Flowing in a Given Resistor for the Corresponding Values of Potential Difference $\text{V}$ Across the Resistor are Given Below: 

Plot a Graph Between $\text{V}$ and $\text{I}$ and Calculate the Resistance of That Resistor.

Ans: The plot between voltage and current is called $\mathbf{I}\text{-V}$ characteristic. 

The voltage is plotted on the x-axis and current is plotted on the y-axis. 

The values of the current for different values of the voltage are shown in the given table. 

The VI characteristic of the given resistor is plotted in the following figure.

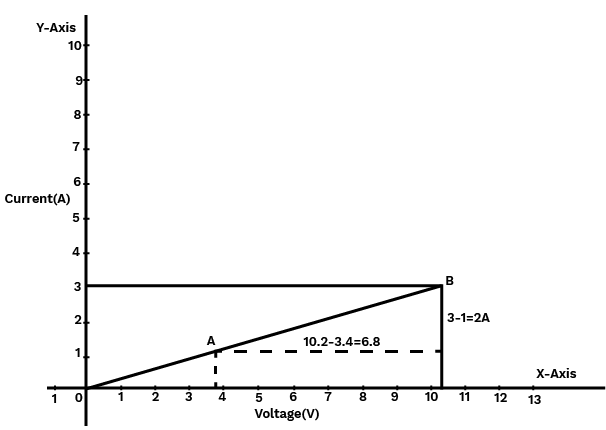
The slope of the line gives the value of resistance $$\left(\text{R}\right)$$as, 

Slope $=\frac{\text{1}}{\text{R}}=\frac{\text{BC}}{\text{AC}}=\frac{\text{2}}{\text{6}\text{.8}}$  

$$\Rightarrow \text{R}=\frac{\text{6}\text{.8}}{\text{2}}=\text{3}\text{.4 }\mathrm{\Omega }$$

Therefore, the resistance of the resistor is $$\text{3}\text{.4 }\mathrm{\Omega }$$. 

8. When a $$\text{12 V}$$ Battery is Connected Across an Unknown Resistor, There is a Current of $$\text{2}\text{.5mA}$$ in the Circuit. Find the value of the Resistance of the Resistor. 

Ans:  

Resistance $$\left(\text{R}\right)$$of a resistor is given by Ohm’s law as, 

$$\text{V = IR }$$

$\Rightarrow \text{R=}\frac{\text{V}}{\text{I}}$

Where, 

Potential difference, $$\text{V = 12 V }$$

Current in the circuit, $$\text{I = 2}\text{.5 mA =2}\text{.5 }\times \text{ 1}{\text{0}}^{\text{-3}}\text{A }$$

$$R=\frac{12}{2.5\times {10}^{-3}}=4.8\times {10}^3\mathrm{\Omega }=4.8k\mathrm{\Omega }$$

Therefore, the resistance of the resistor is $$\text{4}\text{.8 k }\mathrm{\Omega }$$.

9. A Battery of $$\mathbf{9}\mathbf{V}$$ is Connected in Series with Resistors of $$\text{0}\text{.2 }\mathrm{\Omega }\text{ , 0}\text{.3 }\mathrm{\Omega }\text{ , 0}\text{.4 }\mathrm{\Omega }\text{ ,}$$$$\text{0}\text{.5 }\mathrm{\Omega }$$ and $$\text{12 }\mathrm{\Omega }$$ ,  respectively. How Much Current Would Flow through the $$\text{12 }\mathrm{\Omega }$$ resistor? 

Ans: The same current should flow through all the resistances and the circuit as everything is connected in series.  

$$\text{V = IR}$$

$\Rightarrow \text{R=}\frac{\text{V}}{\text{I}}$

Where $\text{R}$ is the equivalent resistance. 

The sum of the resistances will give the value of $\text{R}$. $$\Rightarrow R=0.2+0.3+0.4+0.5+12=13.4\mathrm{\Omega }$$

Potential difference, $$\text{V = 9 V }$$;

$\Rightarrow I=\frac{9}{13.4}=0.671A$

Therefore, the current that would flow through the $$\text{12 }\mathrm{\Omega }$$ resistor is $$\text{0}\text{.671 A}\text{. }$$

10. How Many $$\text{176 }\mathrm{\Omega }$$ resistors (in parallel) are Required to carry $$\text{5 A}$$ on a $$\text{220 V}$$ Line? 

Ans: Let’s assume the number of resistances to be $x$. 

The equivalent resistance of resistors connected in parallel is given by  

$$\frac{1}{R}=x\times \frac{1}{176}$$

$\Rightarrow R=\frac{176}{x}$

Now, Ohm’s law is given as 

$$V=IR$$

$\Rightarrow R=\frac{V}{I}$

Where, 

Supply voltage, $$\text{V = 220 V }$$

Current, $$I=5A$$

So, the equation can be written as,

$$\frac{176}{x}=\frac{220}{5}$$

$$\Rightarrow x=\frac{176}{44}$$

$$\Rightarrow x=4$$

Therefore, four resistors of $$\text{176 }\mathrm{\Omega }$$ are required to draw the given amount of current. 

11. Show How You Would Connect Three Resistors, Each of Resistance

$$\text{6 }\mathrm{\Omega }$$, so that the combination has a resistance of

a). $$\text{9 }\mathrm{\Omega }$$

Two Resistors in Parallel: Consider the following figure.

Two $$\text{6 }\mathrm{\Omega }$$ resistors are connected in parallel. Their equivalent resistance will be 

$R=\frac{1}{\frac{1}{6}+\frac{1}{6}}=\frac{6\times 6}{6+6}=3\mathrm{\Omega }$

The third $$6\mathrm{\Omega }$$ resistor is connected in series with $$\text{3 }\mathrm{\Omega }$$. 

Hence, the equivalent resistance of the circuit is $$\text{6 }\mathrm{\Omega }\text{ + }\text{ 3 }\mathrm{\Omega }\text{ = 9 }\mathrm{\Omega }\text{. }$$

b). $$\text{4 }\mathrm{\Omega }$$

Two Resistors in Series: Consider the following figure. 

Two $$\text{6 }\mathrm{\Omega }$$ resistors are connected in series. 

Their equivalent resistance will be the sum $$R=6+6=12\mathrm{\Omega }$$

The third $$\text{6 }\mathrm{\Omega }$$  resistor is in parallel with $$\text{12 }\mathrm{\Omega }$$. 

Hence, equivalent resistance will be 

$\Rightarrow{{R}_{eq}}=\frac{1}{\frac{1}{12}+\frac{1}{6}}=\frac{12\time

s 6}{12+6}=4\Omega $

Therefore, the total resistance is $$\text{4 }\mathrm{\Omega }$$. 

12. Several Electric Bulbs Designed to be Used on a $$\text{220 V}$$ Electric Supply Line, are Rated $$\text{10W}$$. How Many Lamps can be Connected in Parallel with Each Other Across the Two Wires of $$\text{220 V}$$ line if the maximum allowable current is $$\text{5 A}$$? 

Ans: Resistance $${\text{R}}_{\text{1}}$$ of one bulb is given by the expression, 

$P_1=\frac{V^2}{R_1}$

$\Rightarrow R_1=\frac{V^2}{P_1}$

Where, 

Supply voltage, $$\text{V = 220 V }$$

Maximum allowable current, $$\text{I = 5 A }$$.

Rating of an electric bulb, $${\text{P}}_{\text{1}}\text{= 10 W }$$.

Resistance of one bulb is $R_1=\frac{{\left(220\right)}^2}{10}=4840\mathrm{\Omega }$.

Apply Ohm’s law to circuit with all the bulbs,  

$$\text{V = IR}$$

$\text{R}$is the total resistance of the circuit for x number of electric bulbs. 

$\Rightarrow R=\frac{V}{I}=\frac{220}{5}=44\mathrm{\Omega }$

Resistance of each electric bulb, $${\text{R}}_{\text{1}}\text{= 4840 }\mathrm{\Omega }$$.

Clearly, since the resistors are connected in parallel,

$\frac{1}{R}=\frac{1}{R_1}\times x$

$\Rightarrow x=\frac{R_1}{R}=\frac{4840}{44}=110$

Therefore, $\text{110}$ electric bulbs can be connected in parallel. 

13. A Hot Plate of an Electric Oven Connected to a $$\text{220 V}$$Line has Two Resistance Coils $\text{A}$ and $\text{B}$ , Each of $$\text{24 }\mathrm{\Omega }$$ Resistances, Which May be Used Separately, in Series, or in Parallel. What are the Currents in the Three Cases? 

Ans: The given data in the question is as follows:

Supply voltage, $$\text{V=220 V }$$.

Resistance of one coil, $$\text{R=24 }\mathrm{\Omega }$$.

a) Coils are Used Separately: 

According to Ohm’s law, 

$$\text{V = }{\text{I}}_{\text{1}}{\text{R}}_{\text{1}}$$

Where, 

$${\text{I}}_{\text{1}}$$is the current flowing through the coil. 

$\Rightarrow {\text{I}}_{\text{1}}\text{=}\frac{\text{V}}{{\text{R}}_{\text{1}}}\text{=}\frac{\text{220}}{\text{24}}\text{=9}\text{.166A}$

Therefore, $$\text{9}\text{.16 A}$$current will flow through each coil when used separately. 

b) Coils are Connected in Series: 

Total resistance, $${\text{R}}_{\text{2}}\text{= 24 }\mathrm{\Omega }\text{ + 24 }\mathrm{\Omega }\text{ = 48 }\mathrm{\Omega }$$

According to Ohm’s law, 

$$\text{V=}{\text{I}}_{\text{2}}{\text{R}}_{\text{2}}$$

Where, 

${\text{I}}_{\text{2}}$ is the current flowing through the series circuit. 

$\Rightarrow {\text{I}}_{\text{2}}\text{=}\frac{\text{V}}{{\text{R}}_{\text{2}}}\text{=}\frac{\text{220}}{\text{48}}\text{=4}\text{.58A}$

Therefore, $$\text{4}\text{.58 A}$$current will flow through the circuit when the coils are connected in series.

c) Coils are Connected in Parallel: 

Total resistance,${\text{R}}_{\text{3}}$ is given as 

$R_3=\frac{\text{1}}{\frac{\text{1}}{\text{24}}\text{+}\frac{\text{1}}{\text{24}}}\text{=}\frac{\text{24}}{\text{2}}\text{=12 }\mathrm{\Omega }$

According to Ohm’s law, 

$$\text{V=}{\text{I}}_{\text{3}}{\text{R}}_{\text{3}}$$

Where, 

${\text{I}}_{\text{3}}$is the current flowing through the circuit.

$\Rightarrow {\text{I}}_{\text{3}}\text{=}\frac{\text{V}}{{\text{R}}_{\text{3}}}\text{=}\frac{\text{220}}{\text{12}}\text{=18}\text{.33A}$

Therefore, $$\text{18}\text{.33 A}$$current will flow through the circuit when coils are connected in parallel. 

14. Compare the Power Used in the $$\text{2 }\mathrm{\Omega }$$ Resistor in Each of the Following Circuits: 

a). $$\text{6 V}$$ battery in series with $$\text{1 }\mathrm{\Omega }$$ and $$\text{2 }\mathrm{\Omega }$$ resistors, and  

Ans:  In the question it is given that $$\text{V = 6 V }$$.

$$\text{1 }\mathrm{\Omega }$$ and $$\text{2 }\mathrm{\Omega }$$ resistors are connected in series. 

Therefore, equivalent resistance of the circuit,

$$\text{R=1+2=3 }\mathrm{\Omega }$$

According to Ohm’s law, 

$$\text{V = IR}$$

Where,

$\text{I}$  is the current through the circuit 

$$\Rightarrow \text{I =}\frac{\text{6}}{\text{3}}\text{= 2 A }$$

In series the same current flows in the entire circuit. 

Hence, current flowing through the $$\text{2 }\mathrm{\Omega }$$ resistor is $$\text{2 A}$$ . 

Power is given by the expression, 

$$\text{P=}{\text{I}}^{\text{2}}\text{R = }{\text{2}}^{\text{2}}\times \text{ 2 = 8 W }$$

b). $$\text{4 V}$$ battery in parallel with $$\text{12 }\mathrm{\Omega }$$ and $$\text{2 }\mathrm{\Omega }$$ resistors. 

Ans:  Potential difference, $$\text{V = 4 V }$$.

$\text{12 }\mathrm{\Omega }$ and $$\text{2 }\mathrm{\Omega }$$ resistors are connected in parallel. 

The voltage across each component of a parallel circuit remains the same. Hence, the voltage across $$\text{2 }\mathrm{\Omega }$$ resistor will be $$\text{4 V}$$. 

Power consumed by $$\text{2 }\mathrm{\Omega }$$ resistor is given by 

$$\text{P=}\frac{{\text{V}}^{\text{2}}}{\text{R}}\text{=}\frac{{\text{4}}^{\text{2}}}{\text{2}}\text{= 8 W }$$

Therefore, the power used by $$\text{2 }\mathrm{\Omega }$$ resistor is $\text{8W}$. 

15. Two Lamps, One Rated $$\text{100 W}$$ at $$\text{220 V}$$, and the Other $$\text{60 W}$$at$$\text{220 V}$$, are Connected in Parallel to Electric Mains Supply. What Current is Drawn From the Line if the Supply Voltage is$$\text{220 V}$$? 

Ans: Both the bulbs are in parallel. Therefore, potential difference across each of them will be $$\text{220 V}$$, because voltage same in a parallel circuit. 

Current drawn by the bulb of rating $$\text{100 W}$$is given by, 

Power = Voltage × Current 

Current$\text{ =}\frac{\text{Power}}{\text{Voltage}}\text{=}\frac{\text{100}}{\text{220}}\text{A}$  

Similarly, current drawn by the bulb of rating $$60W$$is given by,

Current $\text{=}\frac{\text{Power}}{\text{Voltage}}\text{=}\frac{\text{60}}{\text{220}}\text{A}$

Hence, total current drawn from the line $\text{=}\frac{\text{100}}{\text{220}}\text{+}\frac{\text{60}}{\text{220}}\text{=0}\text{.727A}$.

16. Which Uses More Energy, a $$\text{250 W}$$ TV set in $\text{1}$hr, or a $$\text{1200 W}$$ Toaster in $\text{10}$ Minutes?

Ans: Energy consumed by an electrical appliance is given by the expression, 

$$\text{H = Pt }$$

Where, 

Power of the appliance$$\text{= P }$$

Time $$\text{= t }$$

Energy consumed by a TV set of power $$\text{250 W}$$ in $\text{1}$h $${\text{E}}_{TV}\text{= 250 }\times \text{ 3600 = 9 }\times \text{ 1}{\text{0}}^{\text{5}}\text{J}$$

Energy consumed by a toaster of power $$\text{1200 W}$$in $\text{10}$ minutes $${\text{E}}_{toaster}\text{= 1200 }\times \text{ 600= 7}\text{.2 }\times \text{ 1}{\text{0}}^{\text{5}}\text{J}$$

Therefore, the energy consumed by a TV set of power $$\text{250 W}$$ in $\text{1}$h is more than the energy consumed by a toaster of power  $$\text{1200 W}$$ in $\text{10}$minutes. 

17. An Electric Heater of Resistance $$\text{8 }\mathrm{\Omega }$$ draws $$\text{15 A}$$ from the service mains $\text{2}$ hours. Calculate the rate at which heat is developed in the heater. 

Ans: Rate of heat produced by a device is given by the expression for power as 

$$\text{P = }{\text{I}}^{\text{2}}\text{R }$$

Where, 

Resistance of the electric heater, $$\text{R = 8 }\mathrm{\Omega }$$

Current drawn, $$\text{I = 15 A }$$

$\Rightarrow \text{P}=\text{1}{\text{5}}^{\text{2}}\times \text{ 8=1800J/s}$

Therefore, heat is produced by the heater at the rate of $$\text{1800 J/s}\text{. }$$

18. Explain the following. 

a). Why is Tungsten Used Almost Exclusively for Filament of Electric Lamps?

Ans: Tungsten has a very high melting point and resistivity.

Due to these properties’, tungsten can produce and maintain high temperatures. 

b). Why are the Conductors of Electric Heating Devices, Such As Bread-Toasters and Electric Irons, Made of an Alloy Rather Than a Pure Metal?

Ans: Alloys have higher melting points than a pure metal. They also are preferred in heating devices because of the heat they produce. This is because of their reduced conductivity which also prevents an electric shock since metals are good conductors while alloys are not.

c). Why is the Series Arrangement Not Used for Domestic Circuits?

Ans: In series arrangement, failure of one component results in failure of the complete circuit. And in series, each device will get different voltages. So parallel connection is preferred over series connection.

d). How Does the Resistance of a Wire Vary With its Area of Cross-Section? 

Ans: Resistance $$\left(\text{R}\right)$$of a wire is inversely proportional to its area of cross-section $$\left(\text{A}\right)\text{,}$$i.e., $\text{R}\propto \frac{\text{1}}{\text{A}}$.

e). Why are Copper and Aluminium Wires Usually Employed for Electricity Transmission?

Ans: Copper and aluminium wires are good conductors of electricity because of their low resistivity. Thus, they are usually employed for transmission of electricity.

NCERT Solutions for Class 10 Science Free PDF Download

NCERT Solutions Chapter 11 Class 10 Science is an effective solution set prepared by famous teachers worldwide. They have prepared the PDF version of the NCERT Solution of Science Class 10 Electricity and have made it available for download. The students can download the solution set as per their convenience on their computer, tablets, or mobiles and study them in their preparation for their respective examinations.

You can Find the Solutions of All the Science Chapters below.

NCERT Solutions for Class 10 Science Chapter 11 

Science Class 10 Chapter 11 deals with various concepts revolving around the main topic of electricity. Let us look into some of these concepts.

Important Topics Covered in Chapter 11 of Class 10 Science NCERT Solutions

Below are the important topics discussed in Chapter 11.

Electric Current and Charge

Science Chapter 11 Class 10 begins with a detailed description of electric current and charge. The NCERT class 10 science chapter 11 solution defines every keyword belonging to the topic. It also describes the key formulas by which these concepts are linked. The concepts are properly represented with schematics and diagrams so that the students understand the details properly. At the end of this section, Class 10 Electricity Exercise Solutions contain some self-evaluating questions. The students can try answering these questions to check their level of understanding of the concepts.

Potential and Potential Difference

In this segment of NCERT Solutions for Class 10 Science Chapter 11, the students will learn about the flow of charge. They are introduced to the concepts of potential and potential difference. The NCERT Solutions for Class 10 Science Electricity will also provide a thorough description of the related parameters’ connection, using formulas to link them. The solution set also shows the application of such formulas. Like the previous segment, the solution set for science NCERT Class 10 Chapter 11 for this segment finishes with several questions for students to evaluate themselves.

Circuit Diagrams

Circuit diagrams are important to represent any electrical circuit. In this segment, the students will learn about the different symbols used to prepare a circuit diagram. This segment includes several diagrams and schematics to elaborate on the details.

Ohm’s Law and Resistance

Another important concept in Class 10 Science Chapter Electricity is resistance. The solution set for 10th Science Chapter 11 explains resistance and its related concepts in detail. The different resistances for different metals have been included. The factors affecting the resistance of a material is also discussed with proper mathematical formulas. The concept of resistors and their combinations are also considered in this solution set. The creators of these notes have included several diagrams to explain the ideas. They have also described Ohm’s law. The mathematical formula associated with it and the application of such laws are also being described elaborately. 

The solution set has been oriented towards exam preparation, and therefore, it also contains several solved examples. These solved mathematical problems are the perfect representation of tough questions that are generally encountered in the examinations. The students can practice these examples and the unsolved questions provided at the end of this segment if they wish to prepare well for their examinations.

Heating Effect of Electric Current and its Application

In the next segment, the heating effect of electric current is discussed in detail. The passage of electrical energy produces heat, and the Joule’s effect measures such a process. The details of Joule’s effect are covered in this section. There are several mathematical formulas associated with Joule’s effect. All these formulas are also included in the solution set for Science Chapter 11 Class 10. The students must practice these solutions hard so that they can get a grasp over the subject.

Along with the details, the solution set for Science Class 10 Chapter 11 also covers the application of such heating effects. The students will learn about real-world applications, which are often referred to during most examinations.

Electric Power

The final concept covered in this solution set is electric power. Before learning about electric power, it is important to understand the individual concepts covered above. As a result, the student will face less difficulty understanding this segment’s details and practice the mathematical formulas associated with it. The solution set also includes several figures and solved and unsolved examples to practice the problems. Such problems carry high marks in examinations, and students can score full marks in these questions if they practice and clear their concepts properly.

At the end of the solution set, all the chapter’s salient points are summarised and listed in a pointwise manner. The students can learn about the entire chapter by studying these points. Such pointwise listing is helpful for students to prepare on the night before the examination. You can find such representations in top online study forums covering Electricity Class 10 like Vedantu. At the end of the solution set, several questions and answers related to the chapter are provided. These questions will help the students build confidence in answering similar questions they face in the examination. 

Exercise Unit 5 total Solutions: 6 Questions (2 short questions 4 Long questions) 

Class 10 Science Chapter 11 - Electricity Weightage 2024-25

Chapter 11 - Electricity of CBSE Class 10 Science holds 12% weightage in the 2024-25 Science board exam. Electricity carries a weightage of around 7 marks, and its important topics include Ohm’s law, the combination of resistors, and the heating effects of current.

Study Materials For Class 10 Science Chapter 11

Chapter-wise NCERT Solutions for Class 10 Science