NCERT Exemplar for Class 10 Maths Chapter 8 - Introduction to Trigonometry & Its Equation (Book Solutions)

Multiple Choice Questions:

Sample Question 1: The value of $\left(\sin 30^{\circ}+\cos 30^{\circ}\right)-\left(\sin 60^{\circ}+\cos 60^{\circ}\right)$ is

A. $-1$

B. 0

C. 1

D. 2

Ans: The correct option is (B)

The values of $\sin 30^{\circ}=\dfrac{1}{2}$, $\cos 30^{\circ}=\dfrac{\sqrt{3}}{2}$, $\sin 60^{\circ}=\dfrac{\sqrt{3}}{2}$, $\cos 60^{\circ}=\dfrac{1}{2}$

Thus, $\left(\sin 30^{\circ}+\cos 30^{\circ}\right)-\left(\sin 60^{\circ}+\cos 60^{\circ}\right)=\left(\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}\right)-\left(\dfrac{\sqrt{3}}{2}+ \dfrac{1}{2}\right)$

$=0$

Sample Question 2: The value of $\dfrac{\tan 30^{\circ}}{\cot 60^{\circ}}$ is

A.  $\dfrac{1}{\sqrt{2}}$

B. $\dfrac{1}{\sqrt{3}}$

C. $\sqrt{3}$

D. 1

Ans: Option (D) is the correct answer.

$\dfrac{\tan 30^{\circ}}{\cot 60^{\circ}}$

$=\dfrac{\tan 30^{\circ}}{\cot \left({90^{\circ}-30^{\circ}}\right)}$

$=\dfrac{\tan 30^{\circ}}{\tan 30^{\circ}}$

$=1$

Sample Question 3: The value of $\left(\sin 45^{\circ}+\cos 45^{\circ}\right)$ is

A. $\dfrac{1}{\sqrt{2}}$

B. $\sqrt{2}$

C. $\dfrac{\sqrt{3}}{2}$

D. 1

Ans: Option B is correct. 

Since, $\sin 45^{\circ}=\dfrac{1}{\sqrt{2}}$ and $\cos 45^{\circ}=\dfrac{1}{\sqrt{2}}$

Thus, $\left(\sin 45^{\circ}+\cos 45^{\circ}\right)=\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{2}}$

$=\dfrac{2}{\sqrt{2}}$=$\sqrt{2}$

Exercise - 8.1

Choose the correct answer from the given four options in the following questions:

1. If $\cos A=\dfrac{4}{5}$, then the value of $\tan A$ is

(a) $\dfrac{3}{5}$

(b) $\dfrac{3}{4}$

(c) $\dfrac{4}{3}$

(d) $\dfrac{5}{3}$

Ans: Option (b) is the correct answer.

$\cos A=\dfrac{B}{H}=\dfrac{4}{5}=\dfrac{4 x}{5 x}$

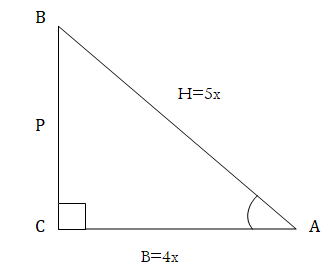
$P^{2}+B^{2}=H^{2}$ (By Pythagoras theorem) 

$\Rightarrow P^{2}+(4 x)^{2}=(5 x)^{2}$

$\Rightarrow P^{2}=25 x^{2}-16 x^{2}$

$\Rightarrow P^{2}=9 x^{2}$

$\Rightarrow P=3 x$

$\therefore \tan A=\dfrac{P}{B}=\dfrac{3 x}{4 x}=\dfrac{3}{4}$ which verifies option (b).

2. If $\sin A=\dfrac{1}{2}$, then the value of $\cot A$ is

(a) $\sqrt{3}$

(b) $\dfrac{1}{\sqrt{3}}$

(c) $\dfrac{\sqrt{3}}{2}$

(d) 1

Ans: Option (a) is the correct answer.

$\sin A=\dfrac{P}{H}=\dfrac{1}{2}=\dfrac{1 x}{2 x}$

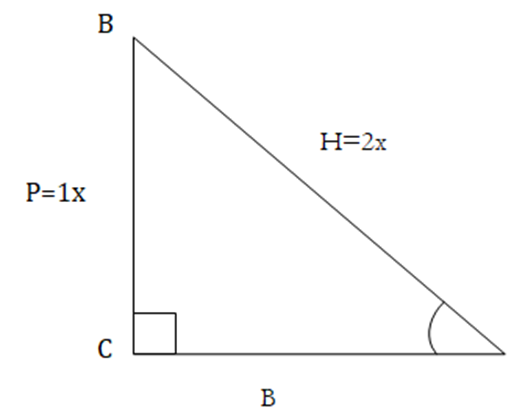
$P^{2}+B^{2}=H^{2} $

$\Rightarrow(1 x)^{2}+B^{2}=(2 x)^{2} $

$\Rightarrow B^{2}=4 x^{2}-1 x^{2}$

$\Rightarrow B^{2}=3 x^{2}$

$\Rightarrow B=\sqrt{3} x$

Now, $\cot A=\dfrac{B}{P}=\dfrac{\sqrt{3}}{1}$=$\sqrt{3}$

Hence, the right option is (a).

3. The value of the expression $\operatorname{cosec}\left(75^{\circ}+\theta\right)-\sec \left(15^{\circ}-\theta\right)-\tan \left(55^{\circ}+\theta\right)+\cot \left(35^{\circ}-\theta\right)$ is

(a) $-1$

(b) $+$

(c) 1

(d) $\dfrac{3}{2}$

Ans: Option (b) is the correct answer.

$\left(75^{\circ}+\theta\right)$ and $\left(15^{\circ}-\theta\right)$ are complements of each other. Similarly, $\left(55^{\circ}+\theta\right)$ and $\left(35^{\circ}-\theta\right)$ are also complements.

So, $\operatorname{cosec}\left(75^{\circ}+\theta\right)-\sec \left(15^{\circ}-\theta\right)-\tan \left(55^{\circ}+\theta\right)+\cot \left(35^{\circ}-\theta\right)$

$=\operatorname{cosec}\left[90^{\circ}-\left(15^{\circ}-\theta\right)\right]-\sec \left(15^{\circ}-\theta\right)-\tan \left(55^{\circ}+\theta\right)+\cot \left[90^{\circ}-\left(55^{\circ}+\theta\right)\right]$

$=\sec \left(15^{\circ}-\theta\right)-\sec \left(15^{\circ}-\theta\right)-\tan \left(55^{\circ}+\theta\right)+\tan \left(55^{\circ}+\theta\right)$

$=0$

Hence, the right option is (b).

4. Given that $\sin \theta=\dfrac{a}{b}$, then $\cos \theta$ is equal to

(a) $\dfrac{b}{\sqrt{b^{2}-a^{2}}}$

(b) $\dfrac{b}{a}$

(c) $\dfrac{\sqrt{b^{2}-a^{2}}}{b}$

(d) $\dfrac{a}{\sqrt{b^{2}-a^{2}}}$

Ans: Option (c) is the correct answer.

 $\sin \theta=\dfrac{P}{H}=\dfrac{a}{b}=\dfrac{a x}{b x}$ [Given]

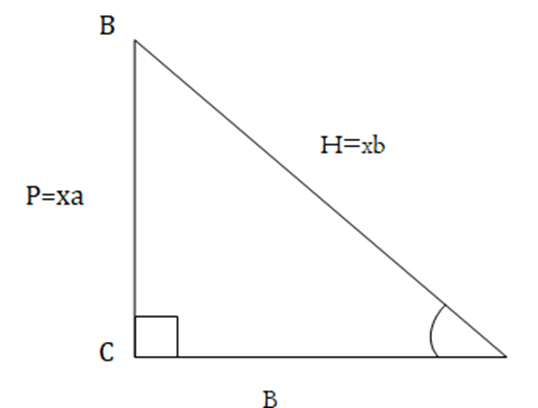
By Pythagoras theorem,

$B^{2}+P^{2}=H^{2} \\$

$\Rightarrow B^{2}+(a x)^{2}=(b x)^{2} \\$

$\Rightarrow B^{2}=b^{2} x^{2}-a^{2} x^{2} \\$

$\Rightarrow B^{2}=x^{2}\left(b^{2}-a^{2}\right) \\$

$\Rightarrow B=x \sqrt{\left(b^{2}-a^{2}\right) }\\$

$\therefore \cos \theta=\dfrac{B}{H}-\dfrac{x \sqrt{b^{2}-a^{2}}}{b x}=\dfrac{\sqrt{b^{2}-a^{2}}}{b}$

which verifies it option (c).

5. If $\cos (\alpha+\beta)=0$, then $\sin (\alpha-\beta)$ can be reduced to

(a) $\cos \beta$

(b) $\cos 2 \beta$

(c) $\sin \alpha$

(d) $\sin 2 \alpha$

Ans: Option (b) is the correct answer.

$\cos (\alpha+\beta)=0$

$\Rightarrow \cos (\alpha+\beta)=\cos 90^{\circ} \\$

$\Rightarrow \alpha+\beta=90^{\circ} \\$

$\Rightarrow \alpha=90^{\circ}-\beta$

Now, $\sin (\alpha-\beta)=\sin \left(90^{\circ}-\beta-\beta\right)$

$=\sin \left(90^{\circ}-2 \beta\right)$

$= \cos 2 \beta$

Hence, verifies the option (b).

6. The value of $\left(\tan 1^{\circ} \tan 2^{\circ} \tan 3^{\circ} \ldots \tan 89^{\circ}\right)$ is

(a) 0

(b) 1

(c) 2

(d) $\dfrac{1}{2}$

Ans: Option (b) is the correct answer.

$\left(\tan 1^{\circ} \tan 2^{\circ} \tan 3^{\circ} \ldots \tan 89^{\circ}\right)$

$=\left(\tan 1^{\circ} \tan 89^{\circ}\right)\left(\tan 2^{\circ} \tan 88^{\circ}\right)\left(\tan 3^{\circ} \tan 87^{\circ}\right) \ldots\left(\tan 45^{\circ} \tan 45^{\circ}\right)$

$=\left[\tan 1^{\circ} \tan \left(90^{\circ}-1\right)\right]\left[\tan 2^{\circ} \tan \left(90^{\circ}-2\right)\right]\left[\tan 3^{\circ} \tan \left(90^{\circ}-3\right)\right] \ldots \tan 45^{\circ} \tan \left(90^{\circ}-45^{\circ}\right)$

$=\tan 1^{\circ} \cot 1^{\circ} \tan 2^{\circ} \cot 2^{\circ} \tan 3^{\circ} \cot 3^{\circ} \ldots \tan 45^{\circ} \cot 45^{\circ}$

$=\tan 1^{\circ} \times \dfrac{1}{\tan 1^{\circ}} \tan 2^{\circ} \cdot \dfrac{1}{\tan 2^{\circ}} \tan 3^{\circ} \cdot \dfrac{1}{\tan 3^{\circ}} \cdots \dfrac{\tan 45^{\circ}}{\tan 45^{\circ}}$

$=1 \cdot 1 \cdot 1 \cdot 1 \ldots 1 \cdot 1$

$=1$

Hence, verifies the option (b).

7. If $\cos 9 \alpha=\sin \alpha$ and $9 \alpha<90^{\circ}$, then the value of $\tan 5 \alpha$ is

(a) $\dfrac{1}{\sqrt{3}}$

(b) $\sqrt{3}$

(c) 1

(d) 0

Ans: Option (c) is the correct answer.

$\cos 9 \alpha=\sin \alpha$

$\Rightarrow \cos 9 \alpha=\cos \left(90^{\circ}-\alpha\right)$

$\Rightarrow 9 \alpha=90^{\circ}-\alpha$

$\Rightarrow 10 \alpha=90^{\circ}$

$\Rightarrow \alpha=9^{\circ}$

$\therefore \tan 5 \alpha=\tan 5 \times 9^{\circ}=\tan 45^{\circ}=1$

Hence, verifies the option (c).

8. If $\triangle A B C$ is right angled at $C$, then the value of $\cos (A+B)$ is

(a) 0

(b) 1

(c) $\dfrac{1}{2}$

(d) $\dfrac{\sqrt{3}}{2}$

Ans: Option (a) is the correct answer.

$\angle A+\angle B+\angle C=180^{\circ}$ (Angle sum property of a triangle)

$\Rightarrow(A+B)+90^{\circ}=180^{\circ} \\$

$\Rightarrow \angle A+\angle B=90^{\circ} \\$

$\Rightarrow \cos (A+B)=\cos 90^{\circ}=0$ 

Hence, verifies option (a).

9. If $\sin A+\sin ^{2} A=1$, then the value of the expression $\left(\cos ^{2} A+\cos ^{4} A\right)$ is

(a) 1

(b) $\dfrac{1}{2}$

(c) 2

(d) 3

Ans: Option (a) is the correct answer. 

$\sin A+\sin ^{2} A=1$ ($\text{Given}$)

$\Rightarrow \sin A=\left(1-\sin ^{2} A\right)$

$\Rightarrow \sin A=\cos ^{2} A$

$\Rightarrow \sin ^{2} A=\cos ^{4} A$ ($\text{Squaring both sides}$)

$\Rightarrow 1-\cos ^{2} A=\cos ^{4} A\left[\because \sin ^{2} A-1-\cos ^{2} A\right]$

$\Rightarrow 1=\cos ^{2} A+\cos ^{4} A$

Hence, verifies the option (a).

10. Given that $\sin \alpha=\dfrac{1}{2}, \cos \beta=\dfrac{1}{2}$, then value of $(\alpha+\beta)$ is

(a) $0^{\circ}$

(b) $30^{\circ}$

(c) $60^{\circ}$

(d) $90^{\circ}$

Ans: Option (d) is the correct answer.

$\sin \alpha=\dfrac{1}{2}[$ Given $]$ $\Rightarrow \sin \alpha=\sin 30^{\circ}$ $\Rightarrow \alpha=30^{\circ}$ Also

$\cos \beta=\dfrac{1}{2} \\$

$\Rightarrow \cos \beta=\cos 60^{\circ} \\$

$\Rightarrow \beta=60^{\circ} \\$

$\therefore \mathrm{a}+\beta=30^{\circ}+60^{\circ}=90^{\circ}$

Hence, verifies the option (d).

11. The value of the expression $\left[\dfrac{\sin ^{2} 22^{\circ}+\sin ^{2} 68^{\circ}}{\cos ^{2} 22^{\circ}+\cos ^{2} 68^{\circ}}+\sin ^{2} 63^{\circ}+\cos 63^{\circ} \sin 27^{\circ}\right]$ is

(a) 3

(b) 2

(c) 1

(d) 0

Ans: Option (b) is the correct answer.

Here, the complement angle of each angle is available. So, by using the formula for complementary angles, we get

${\left[\dfrac{\sin ^{2} 22^{\circ}+\sin ^{2}(90-22)^{\circ}}{\cos ^{2} 22^{\circ}+\cos ^{2}(90-22)^{\circ}}+\sin ^{2} 63^{\circ}+\cos 63^{\circ} \sin (90-63)^{\circ}\right]} \\$

${\left[\dfrac{\sin ^{2} 22^{\circ}+\cos ^{2} 22^{\circ}}{\cos ^{2} 22^{\circ}+\sin ^{2} 22^{\circ}}+\sin ^{2} 63^{\circ}+\cos 63^{\circ} \cos 63^{\circ}\right]} \\$

$= \dfrac{1}{1}+\sin ^{2} 63^{\circ}+\cos ^{2} 63^{\circ}\left[\because \sin ^{2} \theta+\cos ^{2} \theta=1\right]$

$= 1+1=2$

Hence, it verifies option (b).

12. If $4 \tan \theta=3$, then $\left[\dfrac{4 \sin \theta-\cos \theta}{4 \sin \theta+\cos \theta}\right]$ is equal to

(a) $\dfrac{2}{3}$

(b) $\dfrac{1}{3}$

(c) $\dfrac{1}{2}$

(d) $\dfrac{3}{4}$

Ans: Option c is the correct answer.

$\left[\dfrac{4 \sin \theta-\cos \theta}{4 \sin \theta+\cos \theta}\right]$

(Dividing the numerator and denominator throughout cos $\theta$ )

$=\left[\dfrac{4\left(\dfrac{\sin \theta}{\cos \theta}\right)-1}{4\left(\dfrac{\sin \theta}{\cos \theta}\right)+1}\right] $

$=\dfrac{4 \tan\theta -1}{4 \tan\theta +1}={3-1}{3+1}$ $\left[\because 4 \tan \theta=3\right]$

$=\dfrac{2}{4}=\dfrac{1}{2}$

Hence, it verifies option (c).

13. If $\sin \theta-\cos \theta=0$, then the value of $\left(\sin ^{4} \theta+\cos ^{4} \theta\right)$ is

(a) 1

(b) $\dfrac{3}{4}$

(c) $\dfrac{1}{2}$

(d) $\dfrac{1}{4}$

Ans: Option (c) is the correct answer.

$\sin \theta-\cos \theta=0$ [Given]

$\Rightarrow \sin \theta=\cos \theta \\$

$\Rightarrow \sin \theta=\sin \left(90^{\circ}-\theta\right) \\$

$\Rightarrow \theta=90^{\circ}-\theta \\$

$\Rightarrow 2 \theta=90^{\circ} \\$

$\Rightarrow \theta=45^{\circ}$

Now, $\left(\sin ^{4} \theta+\cos ^{4} \theta\right)=\left(\sin^{4} 45+\cos^{4} 45\right)$

$=\left(\dfrac{1}{\sqrt{2}}\right)^{4}+\left(\dfrac{1}{\sqrt{2}}\right)^{2}=\dfrac{1}{4}+\dfrac{1}{4}=\dfrac{2}{4}=\dfrac{1}{2}$

Hence, verifies option (c).

14. $\sin \left(45^{\circ}+\theta\right)-\cos \left(45^{\circ}-\theta\right)$ is equal to

(a) $2 \cos \theta$

(b) 0

(c) $2 \sin \theta$

(d) 1

Ans: Option (b) is the correct answer.

 $\left(45^{\circ}+\theta\right)$ and $\left(45^{\circ}-\theta\right)$ are complementary angles.

$\therefore$ By using formulae of complementary angles,

$=\sin \left(45^{\circ}+\theta\right)-\cos \left(45^{\circ}-\theta\right) \\$

$=\sin \left(45^{\circ}+\theta\right)-\cos \left[90^{\circ}-\left(45^{\circ}+\theta\right)\right] \\$

$=\sin \left(45^{\circ}+\theta\right)-\sin \left(45^{\circ}+\theta\right) \\$

$=0$

Hence, verifies the option (b).

15. If a pole $6 \mathrm{~m}$ high casts a shadow of $2 \sqrt{3} \mathrm{~m}$ long on the ground, then the sun's elevation is

(a) $60^{\circ}$

(b) $45^{\circ}$

(c) $30^{\circ}$

(d) $90^{\circ}$

Ans: Option (a) is the correct answer.

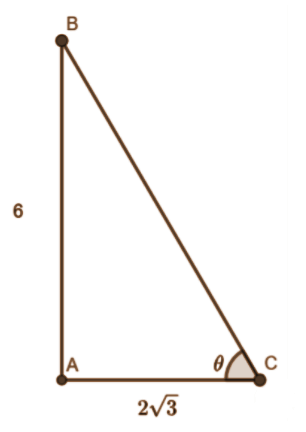
$\tan \theta=\dfrac{6}{2 \sqrt{3}}=\dfrac{3}{\sqrt{3}}=\dfrac{\sqrt{3}}{1}$

$\Rightarrow \tan \theta=\tan 60^{\circ} \\$

$\Rightarrow \theta=60^{\circ}$

Hence, the right option is (a).

Short Answer Questions with Reasoning

Sample Question 1: The value of $\sin \theta+\cos \theta$ is always greater than 1.

Ans: False. 

The value of $(\sin \theta + \cos \theta)$ for $\theta=0^{\circ}$ is 1 .

Sample Question 2: The value of $\tan \theta\left(\theta<90^{\circ}\right)$ increases as $\theta$ increases.

Ans: True. 

In Fig, B is moved closer to C along BC. It is observed that

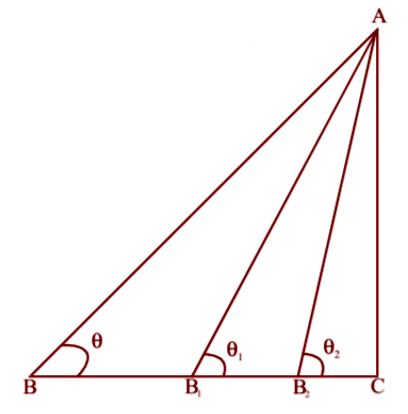
(i) $\theta$ increases $($ as $\theta _{1}>\theta, \theta_{2}>\theta_{1}, \ldots)$ and

(ii) $\mathrm{BC}$ decreases $(\mathrm{B}_{1} \mathrm{C}<\mathrm{BC}, \mathrm{B}_{2} \mathrm{C}<\mathrm{B}_{1} \mathrm{C}, \ldots)$

Thus, the perpendicular $\mathrm{AC}$ remains fixed and the base $\mathrm{BC}$ decreases. Hence $\tan \theta$ increases as $\theta$ increases.

Sample Question 3: $\tan \theta$ increases faster than $\sin \theta$ as $\theta$ increases.

Ans: True.

We know that $\sin \theta$ increases as $\theta$ increases but $\cos \theta$ decreases as $\sin \theta$ increases.

We have $\tan \theta=\dfrac{\sin \theta}{\cos \theta}$

Now as $\theta$ increases, $\sin \theta$ increases but $\cos \theta$ decreases. Therefore, in the case of $\tan \theta$, the numerator increases and the denominator decreases. But in case of $\sin \theta$ which can be seen as $\dfrac{\sin \theta}{1}$, only the numerator increases but the denominator remains fixed at $1 .$

Hence $\tan \theta$ increases faster than $\sin \theta$ as $\theta$ increases.

Sample Question 4: The value of $\sin \theta$ is $a+\dfrac{1}{a}$, where 'a' is a positive number. 

Ans: False. 

We know that $\left(\sqrt{a}-\dfrac{1}{\sqrt{a}}\right)^{2} \geq 0$ or $a+\dfrac{1}{a} \geq 2$,

but $\sin \theta$ is not greater than 1 .

Alternatively, there exists the following three possibilities:

Case 1. If a < 1  then $a+\dfrac{1}{a}> 1$

Case 2. If a $=1$, then $a+\dfrac{1}{a}>1$

Case 3. If a > 1, then $a+\dfrac{1}{a}>1$

However, $\sin \theta$ cannot be greater than 1 .

EXERCISE $8.2$

Write True or False and justify your answer in each of the following:

1.  $\dfrac{\tan 47^{\circ}}{\tan 43^{\circ}}=1$

Ans: True.

$47^{\circ}$ and $43^{\circ}$ are complementary angles.

$\therefore \dfrac{\tan 47^{\circ}}{\cot 43^{\circ}}=\dfrac{\tan 47^{\circ}}{\cot (90-47)^{\circ}}=\dfrac{\tan 47^{\circ}}{\tan 47^{\circ}}=1$

Hence, the given expression is true.

2. The value of the expression $\left(\cos ^{2} 23^{\circ}-\sin ^{2} 67^{\circ}\right)$ is positive.

Ans: False.

 $23^{\circ}$ and $67^{\circ}$ are complementary angles so $\cos ^{2} 23^{\circ}-\sin ^{2} 67^{\circ}=\cos ^{2} 23^{\circ}-\sin ^{2}\left(90^{\circ}-23^{\circ}\right)$

$=\cos ^{2} 23^{\circ}-\cos ^{2} 23^{\circ}$

$=0$

So, the value of the given expression is not positive. Hence, the given statement is false.

3. The value of the expression $\left(\sin 80^{\circ}-\cos 80^{\circ}\right)$ is negative.

Ans: False.

$80^{\circ}$ is nearer to $20^{\circ}, \sin 90^{\circ}=1$ and $\cos 90^{\circ}=0$

So, the given expression $\sin 80^{\circ}-\cos 80^{\circ}>0$

So, the value of the given expression is positive. So, the given statement is false.

4. $\sqrt{\left(1-\cos ^{2} \theta\right)\cdot\sec ^{2} \theta}=\tan \theta$

Ans: True.

 LHS $=\sqrt{\left(1-\cos ^{2} \theta\right)\cdot\sec ^{2} \theta}=\sqrt{\sin ^{2} \theta \cdot \dfrac{1}{\cos ^{2} \theta}}$

$=\sqrt{\dfrac{\sin ^{2} \theta}{\cos ^{2} \theta}}=\tan \theta=$ RHS

Hence, the given expression is true.

5. If $\cos A+\cos ^{2} A=1$, then $\sin ^{2} A+\sin ^{4} A=1$

Ans: True

$\cos A+\cos ^{2} A=1 \text { [Given] } $

$\Rightarrow \cos A=1-\cos ^{2} A $

$\Rightarrow \cos A=\sin ^{2} A $

$\Rightarrow \cos ^{2} A=\sin ^{4} A$

Now, $LHS=\sin ^{2} A+\sin ^{4} A$

$=\cos A+\cos ^{2} A$

$=1\text {=RHS }$

Hence, the given statement is true.

6. $(\tan \theta+2)(2 \tan \theta+1)=5 \tan \theta+\sec ^{2} \theta$

Ans: False

$\text { LHS }=(\tan \theta+2)(2 \tan \theta+1) \\$

$=\tan \theta(2 \tan \theta+1)+2(2 \tan \theta+1)$

$=2 \tan ^{2} \theta+\tan \theta+4 \tan \theta+2 \\$

$=2 \tan ^{2} \theta+5 \tan \theta+2 \\$

$=2\left(\tan ^{2} \theta+1\right)+5 \tan \theta \\$

$=2 \sec ^{2} \theta+5 \tan \theta \neq \text { RHS }$

Hence, the given statement is false.

7. If the length of the shadow of a tower is increasing, then the angle of elevation of the sun is also increasing.

Ans: False.

The shadow of a tower on the ground increases from $x$ to $(x+y)$ when the angle of elevation of the sun changes from ${\theta}_1$ to ${\theta}_2$.

$\therefore {\theta}_1$ is the exterior angle of $\Delta \mathrm{TSD}$

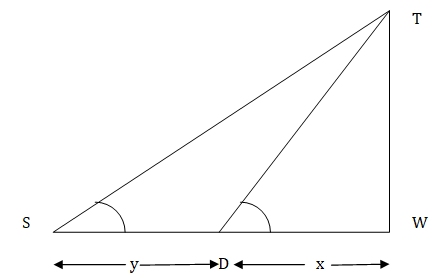
$\text { so } {\theta}_1>{\theta}_2$

So, on increasing the length of the shadow the angle of elevation decreases. Hence, the given statement is false.

8. If a man standing on a platform $3 \mathrm{~m}$ above the surface of a lake observes a cloud and its reflection in the lake, then the angle of elevation of the cloud is equal to the angle of depression of its reflection.

Ans: False.

The observer is at the platform (P) $3 \mathrm{~m}$ above the surface Ik of the lake.

He observes the angle of elevation of cloud C from P, and its reflection image in the lake is formed at I. The observer measures the angle of depression of image (I) $\theta$. Draw PM on the vertical line passing through the cloud and its image.

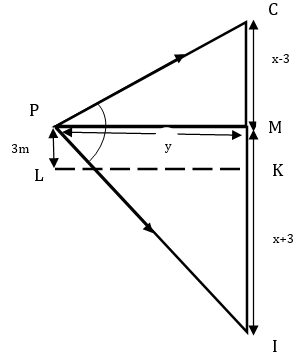
$\mathrm{CK}=\mathrm{KI}=\mathrm{x}$ by the property of reflection $\mathrm{CM}=\mathrm{CK}-\mathrm{MK}=\mathrm{x}-3$

$M I=K I+M K=x+3$

Now, $\tan \theta_{1}=\dfrac{x-3}{y}$ and $\tan \theta_{2}=\dfrac{x+3}{y}$

$\Rightarrow y=\dfrac{x-3}{\tan \theta_{1}}$ And $\Rightarrow y=\dfrac{x+3}{\tan \theta_{2}}$

$\Rightarrow \dfrac{x+3}{\tan \theta_{2}}=\dfrac{x-3}{\tan \theta_{1}}$

$\Rightarrow \tan \theta_{2}=\left(\dfrac{x+3}{x-3}\right) \tan \theta_{1}$

$\Rightarrow \tan \theta \neq \tan \theta_{2}$

Or $\theta_{1} \neq \theta_{2}$

Alternate Method: By the property of image formation, the distance of the image and the object are equal from the reflecting surface.

So, $\mathrm{KC}-\mathrm{KI}$

$\Rightarrow \mathrm{MI}=\mathrm{MC}$

$\Rightarrow \triangle \mathrm{MPC} \neq \triangle \mathrm{MPI}$

So, $\theta_{1} \neq \theta_{2}$

9. The value of $2 \sin \theta$ can be $\left(a+\dfrac{1}{a}\right)$, where a is a positive number, and $a \neq 1$. 

Ans: False.

Consider ' $a$ ' and $: \dfrac{1}{a}$ ' as positive numbers and $\mathrm{a} \neq 0$

Arithmetic mean (AM) of $a$ and $\dfrac{1}{a}=\dfrac{\left(a+\dfrac{1}{a}\right)}{2}$

Geometric mean (GM) of a and $\dfrac{1}{a}=\sqrt{a \times \dfrac{1}{a}}=1$

$\because A M>G M$

$\therefore \dfrac{\left(a+\dfrac{1}{a}\right)}{2}>1 \\$

$\Rightarrow \left(a+\dfrac{1}{a}\right)>2$

Let $a+\dfrac{1}{a}=2 \sin \theta$

$\Rightarrow 2 \sin \theta>2$

$\Rightarrow \sin \theta>1$

Alternate Method: a is positive and a =1 i.e., a can be above 0 to all real and values except1. Let $0<\mathrm{a}<1$ then $\dfrac{1}{a}$ will be move than 1 so $a+\dfrac{1}{a}>2$ for any value of $\mathrm{a}$.

Let $\mathrm{a}-0.2 \Rightarrow a+\dfrac{1}{a}-0.2+\dfrac{1}{0.2}-5.2$

$a-0.9 \Rightarrow a+\dfrac{1}{a}-0.9+\dfrac{1}{0.9}-0.9+1.111-2.011$

Put $a+\dfrac{1}{a}-2 \sin \theta$

$\therefore 2 \sin \theta>2$

$\Rightarrow \sin \theta>1$

which is impossible so $2 \sin \theta \neq a+\dfrac{1}{a}$

Hence, the given statement is false. If we take any value of a more than one, then

the value of $a+\dfrac{1}{a}$ is always greater than 2 which repeats the result.

10. $\cos \theta=\dfrac{a^{2}+b^{2}}{2 a b}$, where $\mathrm{a}$ and $\mathrm{b}$ are two distinct numbers such that $\mathrm{ab}>0$.

Ans: False.

 Consider two numbers $a^{2}$ and $b^{2}$ then

Arithmetic mean (AM) of $a^{2}$ and $b^{2}=\dfrac{a^{2}+b^{2}}{2}$

Geometric mean $(G M)$ of $a^{2}$ and $b^{2}=\sqrt{a^{2}\times b^{2}}$

$\Rightarrow \mathrm{GM}=\mathrm{ab} \\$

$\because \mathrm{AM}>\mathrm{GM} \\$

$\therefore \dfrac{\mathrm{a}^{2}+\mathrm{b}^{2}}{2}>\mathrm{ab} \\$

$\Rightarrow \dfrac{\mathrm{a}^{2}+\mathrm{b}^{2}}{2 a b}>1 \\$

$\Rightarrow \cos \theta>1 \left( \text { Given } \cos \theta=\dfrac{\mathrm{a}^{2}+\mathrm{b}^{2}}{2 a b}\right)$

But, the value of $\cos \theta$ never be greater than 1 .

So, the given expression is false.

11. The angle of elevation of the top of a tower is $30^{\circ}$. If the height of the tower is doubled, then the angle of elevation of its top will also be doubled.

Ans: False. 

Let the height of the tower is, $\mathrm{h}$. For the observer at $\mathrm{A}$ the angle of elevation is equal to $30^{\circ}$.

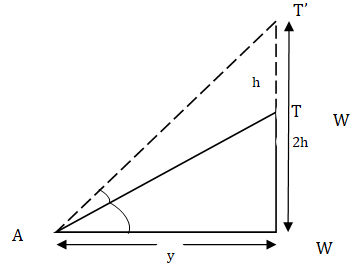
$\tan 30^{\circ}=\dfrac{h}{y} \\$

$\Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{h}{y} \\$

$\Rightarrow \mathrm{y}=h \sqrt{3}$

Now, the height of the tower increases to $2 \mathrm{~h}$.

Now, let the new angle of elevation at $\mathrm{A}$ becomes $\theta$ then

$\tan \theta=\dfrac{2 h}{y} \\$

$\Rightarrow \tan \theta=\dfrac{2 h}{h \sqrt{3}} \\$

$\Rightarrow \tan \theta=\dfrac{2}{\sqrt{3}}$

But, $\tan 60^{\circ}=\sqrt{3}$

$\Rightarrow \tan 60^{\circ}=\sqrt{3} \neq \dfrac{2}{\sqrt{3}}$

$\text { So, } \theta \neq 60^{\circ}$

Hence, the angle of elevation can not be doubled, so the given statement is false.

12. If the height of a tower and the distance of the point of observation from its foot both are increased by $10 \%$, then the angle of elevation of its top remains: unchanged. 

Ans: True.

Let height $\mathrm{h}$ of tower TW makes an angle of elevation $\theta$ to the observer at $\mathrm{A}$ and the distance from foot of tower to the observer is $x$.

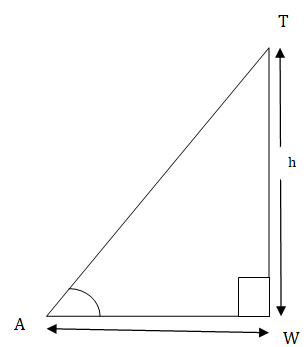
$\therefore \tan \theta=\dfrac{h}{x}...............(\mathrm{I})$

Now, $h$ and $x$ increases by $10 \%$

$\therefore h^{\prime}=h+10 \% \text { of } h = h+\dfrac{10}{100} \times h=h+0.1 h $

$\Rightarrow h^{\prime}=1.1 h$

Similarly, $x^{\prime}=1.1 x$

$\therefore \tan \theta^{\prime}=\dfrac{1.1 h}{1.1 x}=\dfrac{h}{x}................(I I)$

From (I) and (II), we get

$\tan \theta=\tan \theta^{\prime} \\$

$\Rightarrow \theta=\theta^{\prime}$

Hence, the given statement is true.

Short Answer Questions

Sample Question 1: Prove that $\sin ^{6} \theta+\cos ^{6} \theta+3 \sin ^{2} \theta \cos ^{2} \theta=1$

Ans: We know that $\sin ^{2} \theta+\cos ^{2} \theta=1$

Therefore, $\left(\sin ^{2} \theta+\cos ^{2} \theta\right)^{3}=1$

or, $\left(\sin ^{2} \theta\right)^{3}+\left(\cos ^{2} \theta\right)^{3}+3 \sin ^{2} \theta \cos ^{2} \theta\left(\sin ^{2} \theta+\cos ^{2} \theta\right)=1$

or, $\sin ^{6} \theta+\cos ^{6} \theta+3 \sin ^{2} \theta \cos ^{2} \theta=1$

Sample Question 2: Prove that $\left(\sin ^{4} \theta-\cos ^{4} \theta+1\right) \operatorname{cosec}^{2} \theta=2$

Ans: L.H.S. $=\left(\sin ^{4} \theta-\cos ^{4} \theta+1\right) \operatorname{cosec}^{2} \theta $

$=\left[\left(\sin ^{2} \theta-\cos ^{2} \theta\right)\left(\sin ^{2} \theta+\cos ^{2} \theta\right)+1\right] \operatorname{cosec}^{2} \theta \\$

$=\left(\sin ^{2} \theta-\cos ^{2} \theta+1\right) \operatorname{cosec}^{2} \theta\left[\text { Because } \sin ^{2} \theta+\cos ^{2} \theta=1\right] $

$=2 \sin^{2} \theta \operatorname{cosec}^{2} \theta$ $\left[\text{ Because } 1-\cos^{2} \theta=\sin^{2} \theta\right]$

$=2=\text { RHS }$

Sample Question 3: Given that $\alpha+\beta=90^{\circ}$, show that $\sqrt{\cos \alpha \operatorname{cosec} \beta-\cos \alpha \sin \beta}=\sin \alpha$

Ans: $\sqrt{\cos \alpha \operatorname{cosec} \beta-\cos \alpha \sin \beta}=\sin \alpha$

$=\sqrt{\cos \alpha \operatorname{cosec}\left(90^{\circ}-\alpha\right)-\cos \alpha \sin \left(90^{\circ}-\alpha\right)} \\$

$=\sqrt{\cos \alpha \sec \alpha-\cos \alpha \operatorname{cos} \alpha} \\$

$=\sqrt{1-\cos ^{2} \alpha} \\$

$=\sin \alpha$

Sample Question 4: If $\sin \theta+\cos \theta=\sqrt{3}$, then prove that $\tan \theta+\cot \theta=1$

Ans: $\sin \theta+\cos \theta=\sqrt{3}$ (given)

$\Rightarrow (\sin \theta+\cos \theta)^{2}=3$

$\Rightarrow \sin ^{2} \theta+\cos ^{2} \theta+2 \sin \theta \cos \theta=3$

$\Rightarrow  2 \sin \theta \cos \theta=2\left[\sin ^{2} \theta+\cos ^{2} \theta=1\right]$

$\Rightarrow \sin \theta \cos \theta=1=\sin ^{2} \theta+\cos ^{2} \theta$

$\Rightarrow  1=\dfrac{\sin ^{2} \theta+\cos ^{2} \theta}{\sin \theta \cos \theta}$

Therefore, $\tan \theta+\cot \theta=1$

EXERCISE $8.3$

Prove the following questions (from 1 to 7 ):

1. $\dfrac{\sin \theta}{(1+\cos \theta)}+\dfrac{(1+\cos \theta)}{\sin \theta}=2 \operatorname{cosec} \theta$

Ans: (i) If there is $(+)$ ve or $(-)$ ve sign in $D^{\prime}$ and $N$ of the expression, then keep the expression in brackets.

(ii) LHS is more difficult than RHS so we will start from LHS.

(iii) Use identities, if applicable.

(iv) Convert the expression into $\sin \theta$ and $\cos \theta$.

LHS $=\dfrac{\sin \theta}{(1+\cos \theta)}+\dfrac{(1+\cos \theta)}{\sin \theta}$

$=\dfrac{\sin ^{2} \theta+(1+\cos \theta)^{2}}{(1+\cos \theta) \sin \theta} \\$

$=\dfrac{\sin ^{2} \theta+(1)^{2}+(\cos \theta)^{2}+2(1)(\cos \theta)}{(1+\cos \theta) \sin \theta}$

$=\dfrac{\sin ^{2} \theta+\cos ^{2} \theta+2 \cos \theta+1}{(1+\cos \theta) \sin \theta}\left[\because \sin ^{2} \theta+\cos ^{2} \theta=1\right] \\$

$=\dfrac{2+2 \cos \theta}{\sin \theta(1+\cos \theta)}=\dfrac{2(1+\cos \theta)}{\sin \theta(1+\cos \theta)} \\$

$=\dfrac{2}{\sin \theta} \\$

$=2 \operatorname{cosec} \theta \\$

$\therefore \text { LHS } = \text { RHS }$

Hence proved.

2. $\dfrac{\tan A}{1+\sec A}-\dfrac{\tan A}{1-\sec A}=2 \operatorname{cosec} A$

Ans: We will start from LHS.

We can take $\tan A$ as common and $(1-\sec A)(1+\sec A)$ makes $\left(1-\sec ^{2} A=\tan ^{2} A\right)$ so formulae will be used.

LHS $=\dfrac{\tan A}{1+\sec A}-\dfrac{\tan A}{1-\sec A}$ $-\tan A\left[\dfrac{1}{1+\sec A}-\dfrac{1}{1-\sec A}\right][$ Taking tanA common $]$

$=\tan A\left[\dfrac{1-\sec A-(1+\sec A)}{(1+\sec A)(1-\sec A)}\right][\text { Taking LCM }] \\$

$=\tan A\left[\dfrac{-2 \sec A}{1-\sec ^{2} A}\right] \\$

$=\dfrac{\tan A(-2 \sec A)}{-\left(\sec ^{2} A-1\right)} \\$

$=\dfrac{-\tan A 2 \sec A}{-\tan ^{2} A} \\$

$=\dfrac{2 \sec A}{\tan A} \\$

$=\dfrac{2 \times \dfrac{1}{\cos A}}{\dfrac{\sin A}{\cos A}} \\$

$=\dfrac{2}{\sin A} \\$

$=2 \operatorname{cosec} A-\mathrm{RHS}$

Hence, proved.

3. If $\tan A=\dfrac{3}{4}$, then $\sin A \cos A=\dfrac{12}{25}$.

Ans: $\tan \mathrm{A}=\dfrac{3}{4}$ (Given) 

$\Rightarrow \tan \mathrm{A}=\dfrac{P}{B}-\dfrac{3 x}{4 x}$

$\mathrm{H}^{2}=\mathrm{p}^{2}+\mathrm{B}^{2}$ (By Pythagoras theorem)

$=(3 \mathrm{x})^{2}+(4 \mathrm{x})^{2}=9 \mathrm{x}^{2}+16 \mathrm{x}^{2} \\$

$\Rightarrow \mathrm{H}^{2}=25 \mathrm{x}^{2} \\$

$\Rightarrow \mathrm{H}=5 \mathrm{x} \\$

$\therefore \sin \mathrm{A}=\dfrac{P}{H}=\dfrac{3 x}{5 x}=\dfrac{3}{5} \\$

$\text { and } \cos \mathrm{A}=\dfrac{B}{H}=\dfrac{4 x}{5 x}=\dfrac{4}{5} \\$

$\therefore \text { LHS }=\sin \mathrm{A} \cos \mathrm{A} \\$

$=\mathrm{RHS}$

Hence, verified.

4.  $ (\sin \alpha+\cos \alpha)(\tan \alpha+\cot \alpha)=\sec \alpha+\operatorname{cosec} \alpha $

Ans: LHS  

$=(\sin \alpha+\cos \alpha)(\tan \alpha+\cot \alpha) \\$

$=(\sin \alpha+\cos \alpha)\left(\dfrac{\sin \alpha}{\cos \alpha}+\dfrac{\cos \alpha}{\sin \alpha}\right) \\$

$=(\sin \alpha+\cos \alpha)\left(\dfrac{\sin ^{2} \alpha+\cos ^{2} \alpha}{\sin \alpha \cos \alpha}\right) \\$

$=(\sin \alpha+\cos \alpha)\left(\dfrac{1}{\sin \alpha \cos \alpha}\right)\left[\because \sin ^{2} \alpha+\cos ^{2} \alpha=1\right] \\$

$=\dfrac{\sin \alpha}{\sin \alpha \cos \alpha}+\dfrac{\cos \alpha}{\sin \alpha \cos \alpha}\\$

${=\dfrac{1}{\cos \alpha}+\dfrac{1}{\sin \alpha}} \\$

$=\sec \alpha+\operatorname{cosec} \alpha \\$

$=RHS$

Hence proved.

5. $(\sqrt{3}+1)\left(3-\cot 30^{\circ}\right)=\tan ^{3} 60^{\circ}- 2 \sin 60^{\circ} $

Ans: LHS $=(\sqrt{3}+1)\left(3-\cot 30^{\circ}\right)$

$=(\sqrt{3}+1)(3-\sqrt{3})$

$=\sqrt{3}(3-\sqrt{3})+1(3-\sqrt{3}) \\$

$=3 \sqrt{3}-3+3-\sqrt{3} \\$

$=2 \sqrt{3} \\$

$\text { RHS }=\tan ^{3} 60^{\circ}-2 \sin 60^{\circ} \\$

$=(\sqrt{3})^{5}-2 \times \dfrac{\sqrt{3}}{2} \\$

$=3 \sqrt{3}-\sqrt{3} \\$

$=2 \sqrt{3} \\$

$\text { LHS }=\text { RHS }$

Hence, proved.

6. $1+\dfrac{\cot ^{2} \alpha}{(1+\operatorname{cosec} \alpha)}=\operatorname{cosec} \alpha$

Ans: LHS = $1+\dfrac{\cot ^{2} \alpha}{(1+\operatorname{cosec} \alpha)} \\$

$=1+\dfrac{\left(\operatorname{cosec}^{2} \alpha-1\right)}{(1+\operatorname{cosec} \alpha)}[\because \cot 2 \alpha=\operatorname{cosec} 2 \alpha-1] \\$

$=1+\dfrac{(\operatorname{cosec} \alpha-1)(\operatorname{cosec}\alpha+1)}{(1+\operatorname{cosec} \alpha)}\left[\because \mathrm{a}^{2}-\mathrm{b}^{2}=(\mathrm{a}-\mathrm{b})(\mathrm{a}+\mathrm{b})\right] \\$

$=\operatorname{cosec} \alpha\\$

Hence proved.

7. $\tan \theta+\tan \left(90^{\circ}-\theta\right)=\sec \theta \sec \left(90^{\circ}-\theta\right) $

Ans: LHS $=\tan \theta+\tan \left(90^{\circ}-\theta\right) \\$

$=\tan \theta+\cot \theta \\$

$=\dfrac{\sin \theta}{\cos \theta}+\dfrac{\cos \theta}{\sin \theta} \\$

$=\dfrac{\sin ^{2} \theta+\cos ^{2} \theta}{\sin \theta \cos \theta} \\$

$=\dfrac{1}{\sin \theta \cos \theta}\left[\because \sin ^{2} \theta+\cos ^{2} \theta=1\right] \\$

$=\operatorname{cosec} \theta \cdot \sec \theta \\$

$\Rightarrow \text { LHS=} \operatorname{cosec} \theta \cdot \sec \theta\\$

RHS $=\sec \theta \sec \theta\left(90^{\circ}-\theta\right)$

$=\sec \theta \operatorname{cosec} \theta$

$\text { LHS }=\text { RHS }$

Hence, verified.

8. Find the angle of elevation when the shadow of a pole ' $h$ ' $m$ high is $\sqrt{3} h {~m}$ long. 

Ans: Height of pole=PL$=h$

Length of shadow = $L=h \sqrt{3}$

$\therefore \tan \theta=\dfrac{h}{h \sqrt{3}} $

$\Rightarrow  \tan \theta=\tan 30^{\circ} $

$\Rightarrow  \theta=30^{\circ}$

Hence, the angle of elevation is $30^{\circ}$.

9. If $\sqrt{3} \tan \theta=1$, then find the value of $\sin ^{2} \theta-\cos ^{2} \theta$.

Ans: $\sqrt{3} \tan \theta=1$

$\Rightarrow \tan \theta=\dfrac{1}{\sqrt{3}}$

$\Rightarrow \tan \theta=\tan 30^{\circ}$

$\Rightarrow \theta=30^{\circ}$

So, $\sin ^{2} \theta-\cos ^{2} \theta=\sin ^{2} 30^{\circ}-\cos ^{2} 30^{\circ}\left[\because \theta=30^{\circ}\right]$

$=\left(\dfrac{1}{2}\right)^{2}-\left(\dfrac{\sqrt{3}}{2}\right)^{2}=\dfrac{1}{4}-\dfrac{3}{4}=\dfrac{-2}{4}=\dfrac{-1}{2}$

10. A ladder $15 \mathrm{~m}$ long just reaches the top of a vertical wall. If the ladder makes an angle of $60^{\circ}$ with the wall, find the height of the wall.

Ans: 

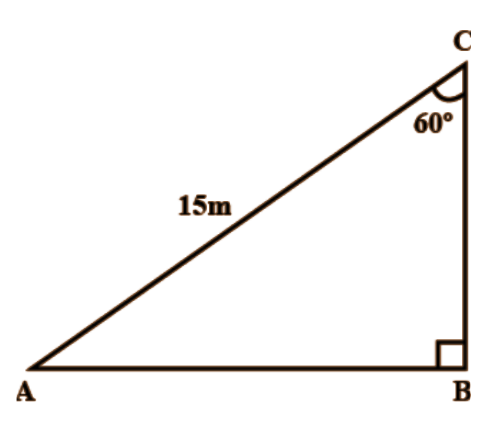
Consider the vertical wall CB $= x \mathrm{~m}$ (let)

Length of inclined ladder AC=15m [Given]

Ladder makes an angle of $60^{\circ}$ with the wall.

$\therefore \dfrac{x}{15}=\cos 60^{\circ}$

$\Rightarrow \dfrac{x}{15}=\dfrac{1}{2}$

$\Rightarrow x=\dfrac{15}{2}=7.5$

Hence, the height of the wall $=7.5 \mathrm{~m}$.

11. Simplify: $\left(1+\tan ^{2} \theta\right)(1-\sin \theta)(1+\sin \theta) $

Ans: $\left(1+\tan ^{2} \theta\right)(1-\sin \theta)(1+\sin \theta)$

$=\left(\sec ^{2} \theta\right)\left(1-\sin ^{2} \theta\right)$

$=\sec ^{2} \theta \cos ^{2} \theta$

$=\dfrac{1}{\cos ^{2} \theta} \times \cos ^{2} \theta$

$=1$

12. If $2 \sin ^{2} \theta-\cos ^{2} \theta=2$, then find the value of $\theta$. 

Ans: Given: $2 \sin ^{2} \theta-\cos ^{2} \theta=2$

$\Rightarrow 2 \sin ^{2} \theta-\left(1-\sin ^{2} \theta\right)=2$

$\Rightarrow 2 \sin ^{2} \theta-1+\sin ^{2} \theta=2$

$\Rightarrow 3 \sin ^{2} \theta=2+1$

$\Rightarrow \sin ^{2} \theta=\dfrac{3}{3}=1$

$\Rightarrow \sin \theta=+1,-1$

$\Rightarrow \sin \theta=1$

$\Rightarrow \sin \theta=\sin 90^{\circ}$

$\Rightarrow \theta=90^{\circ}$

$\Rightarrow \sin \theta=-1$

$\Rightarrow \sin \theta=-\sin 90^{\circ}$

$\Rightarrow-\sin (-\theta)=-\sin 90^{\circ}$

$\Rightarrow \sin (-\theta)=\sin 90^{\circ}$

$\Rightarrow-\theta=90^{\circ}$

$\Rightarrow \theta=-90^{\circ}$

$\text { i.e, } \theta=360^{\circ}-90^{\circ}=270^{\circ}$

Hence, $\theta=90^{\circ}$ and $270^{\circ}$

13. Show that $\dfrac{\cos ^{2}(45^{\circ}+\theta)+\cos ^{2}(45^{\circ}-\theta)}{\tan (60^{\circ}+\theta) \tan (30^{\circ}-\theta)}=1$.

Ans: $\left(45^{\circ}+\theta\right),\left(45^{\circ}-\theta\right)$ and $\left(60^{\circ}+\theta\right),\left(30^{\circ}-\theta\right)$ are complementary angles so by using complementary angle formulae, we get

$\dfrac{\cos ^{2}(45^{\circ}+\theta)+\cos ^{2}(45^{\circ}-\theta)}{\tan \left(60^{\circ}+\theta\right) \tan \left(30^{\circ}-\theta\right)}\left[\because 90^{\circ}-\left(45^{\circ}-\theta\right)=90^{\circ}-45^{\circ}+\theta=45^{\circ}+\theta\right] \\$

$\dfrac{\cos ^{2}(45^{\circ}+\theta)+\sin ^{2}(45^{\circ}+\theta)}{\tan \left(60^{\circ}+\theta\right) \cot \left(60^{\circ}+\theta\right)} \\$

$=\dfrac{1}{\tan (60^{\circ}+\theta) \cdot \dfrac{1}{\tan \left(60^{\circ}+\theta\right)}} \\$

$=\dfrac{1}{1}=1=\text { RHS }$

Hence proved.

14. An observer $1.5 \mathrm{~m}$ tall is $20.5 \mathrm{~m}$ away from a tower $22 \mathrm{~m}$ high. Determine the angle of elevation of the top of the tower from the eye of the observer.

Ans: Height of tower $(AB) =22.5 \mathrm{~m}$ [Given]

Height of observer $(MB)=1.5 \mathrm{~m}$ [Given]

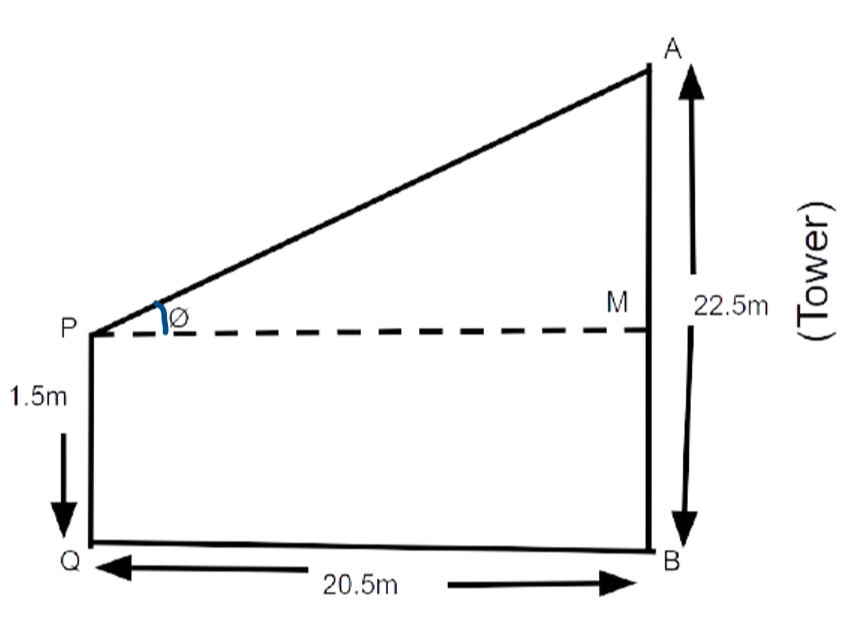
Distance between the foot of tower and observer (BQ) $=20.5 \mathrm{~m}$ [Given]

Let $\theta=$ angle of elevation of the observer at the top of the tower.

Now, AM = 22m-1.5m=20.5m

$A M=20.5 \mathrm{~m} $

$\therefore \tan \theta=\dfrac{20.5}{20.5}=1 $

$\Rightarrow \tan \theta=1$

$\Rightarrow \tan \theta=\tan 45^{\circ} $

$\Rightarrow \theta=45^{\circ}$

Hence, the angle of elevation of the top of the tower from the observer's eye is $45^{\circ}$.

15. Show that $\tan ^{4} \theta+\tan ^{2} \theta=\sec ^{4} \theta-\sec ^{2} \theta$.

Ans: $\tan ^{2} \theta$ or $\tan ^{4} \theta$ can be converted into $\sec ^{2} \theta$

$\text { So, LHS = } \tan ^{2} \theta+\tan ^{2} \theta \\$

$=\tan ^{2} \theta\left(\tan ^{2} \theta+1\right) \\$

$=\left(\sec ^{2} \theta-1\right) \sec ^{2} \theta\left[\because \tan ^{2} \theta=\sec ^{2} \theta-1, \tan ^{2} \theta+1=\sec ^{2} \theta\right] \\$

$=\sec ^{4} \theta-\sec ^{2} \theta \\$

$=\text { RHS }$

Hence, proved.

Long Answer Questions:

Sample Question 1: A spherical balloon of radius r subtends an angle $\theta$ at the eye of an observer. If the angle of elevation of its centre is $\varphi$, find the height of the centre of the balloon.

Ans: In Fig, $O$ is the center of a balloon, whose radius $O P=r$ and $\angle P A Q=\theta$.

$\mathrm{Also}, \angle \mathrm{OAB}=\varphi .$

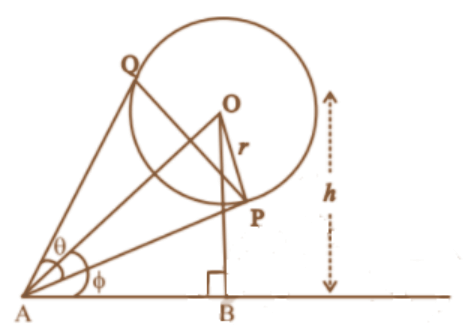
Let the height of the center of the balloon be $h$.

Thus $\mathrm{OB}=\mathrm{h}$.

Now, from $_{\triangle} \mathrm{OAP}$,

$\sin \dfrac{\theta}{2}=\dfrac{\mathrm{r}}{d}$, where $\mathrm{OA}=\mathrm{d} \ldots$ (i)

Also from $_{\triangle} \mathrm{OAB}, \sin \phi=\dfrac{h}{d} .$

From (1) and (2), we get 

$\dfrac{\sin \phi}{\sin \dfrac{\theta}{2}}=\dfrac{\dfrac{h}{d}}{\dfrac{r}{d}}=\dfrac{h}{r} $

$\Rightarrow \mathrm{h}=r \sin \varphi \operatorname{cosec} \dfrac{\theta}{2}$.

Sample Question 2: From a balloon vertically above a straight road, the angles of depression of two cars at an instant are found to be $45^{\circ}$ and $60^{\circ}$. If the cars are $100 \mathrm{~m}$ apart, find the height of the balloon.

Ans: Let the height of the balloon at $\mathrm{A}$ be $\mathrm{h}$ meters.

Let $\mathrm{P}$ and $\mathrm{Q}$ be the two cars.

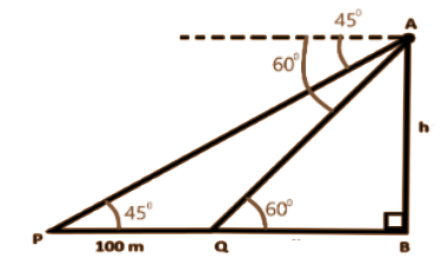
Thus $PQ=100 \mathrm{~m}$.

From $\triangle \mathrm{APB}$

$\mathrm{PB}=\mathrm{AB}=\mathrm{h}$

Now from $\triangle \mathrm{AQB}$,

$\dfrac{AB}{BQ}=\tan 60^{\circ}=\sqrt{3} \\$

$\dfrac{h}{h-100}=\sqrt{3}$

Therefore,

$h=\dfrac{100 \sqrt{3}}{\sqrt{3}-1}=50(3+\sqrt{3}) m$

i.e., the height of the balloon is $50(3+\sqrt{3}) \mathrm{m}$.

Sample Question 3: The angle of elevation of a cloud from a point $h$ meters above the surface of a lake is $\theta$ and the angle of depression of its reflection in the lake is $\phi$. Prove that the height of the cloud above the lake is $h\left(\dfrac{\tan \phi+\tan \theta}{\tan \phi-\tan \theta}\right)$.

Ans: Let $P$ be the cloud and $Q$ be its reflection in the lake (see Fig.). Let $A$ be the point of observation such that $A B=h$.

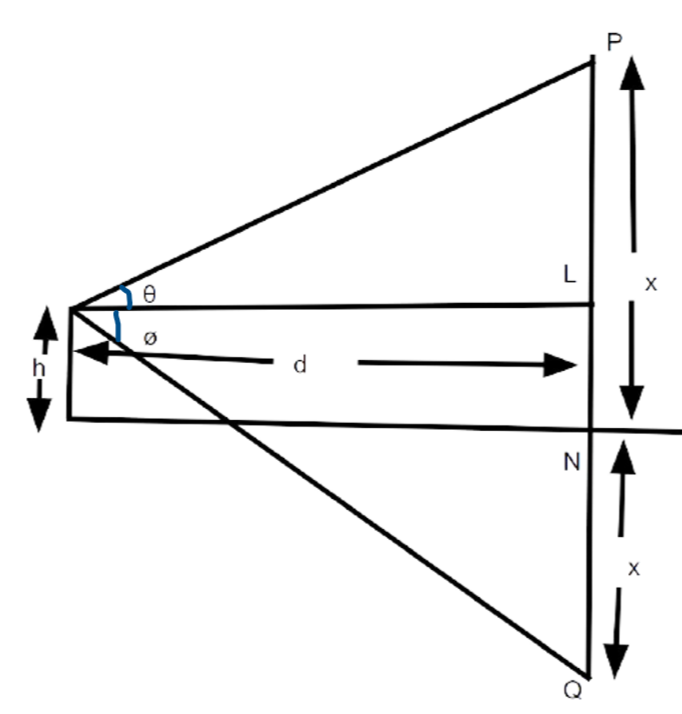
Let the height of the cloud above the lake be $x$.

Let $A L=d$.

Now from ${\triangle PAL}$,

$\dfrac{x-h}{d}=\tan \theta \ldots(i)$

From ${\triangle}$ QAL ,

$\dfrac{x+h}{d}=\tan \phi \ldots \text { (ii) }$

From (1) and (2), we get

$\dfrac{x+h}{x-h}=\dfrac{\tan \phi}{\tan \theta} $

$\Rightarrow \dfrac{2 x}{2 h}=\dfrac{\tan \phi+\tan \theta}{\tan \phi-\tan \theta}$

Therefore, $x=h\left(\dfrac{\tan \phi+\tan \theta}{\tan \phi-\tan \theta}\right)$.

EXERCISE 8.4

1. If $\operatorname{cosec} \theta+\cot \theta=p$, then prove that cos $\theta=\dfrac{p^{2}-1}{p^{2}+1}$.

Ans: $\operatorname{cosec} \theta+\cot \theta=p$ [Given]

$\Rightarrow \dfrac{1}{\sin \theta}+\dfrac{\cos \theta}{\sin \theta}=p \\$

$\Rightarrow \dfrac{1+\cos \theta}{\sin \theta}=p$

Squaring Both Sides, We get

$\Rightarrow \dfrac{(1+\cos \theta)^{2}}{\sin^{2} \theta}=p^{2} \\$

$\Rightarrow \dfrac{(1+\cos \theta)^{2}}{(1-\cos^{2} \theta)}=p^{2} \\$

$\Rightarrow \dfrac{(1+\cos \theta)^{2}}{(1-\cos \theta)(1+\cos \theta)}=p^{2} \\$

$\Rightarrow \dfrac{1+\cos \theta}{1-\cos \theta}=\dfrac{p^{2}}{1}$

By using the rule of componendo and dividendo $\dfrac{a}{b}=\dfrac{c}{d}$ can be written as $ \dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}$ So, by using componendo and dividendo, we have

$\dfrac{(1+\cos \theta)+(1-\cos \theta)}{(1+\cos \theta)-(1-\cos \theta)}=\dfrac{p^{2}+1}{p^{2}-1} \\$

$\Rightarrow \dfrac{2}{2 \cos \theta}=\dfrac{p^{2}+1}{p^{2}-1} \\$

$\Rightarrow \cos \theta=\dfrac{p^{2}-1}{p^{2}+1}$

Hence, proved.

2. Prove that $\sqrt{\sec ^{2} \theta+\operatorname{cosec}^{2} \theta}=\tan \theta+\cot \theta$.

Ans: LHS $=\sqrt{\sec ^{2} \theta+\operatorname{cosec}^{2} \theta}$

$=\sqrt{\dfrac{1}{\cos ^{2} \theta}+\dfrac{1}{\sin ^{2} \theta}}=\sqrt{\dfrac{\sin ^{2} \theta+\cos ^{2} \theta}{\cos ^{2} \theta \sin ^{2} \theta}}$

$=\sqrt{\dfrac{1}{\cos ^{2} \theta \cdot \sin ^{2} \theta}} \\$

$=\dfrac{1}{\cos \theta \sin \theta} \\$

$=\operatorname{cosec} \theta \sec \theta \\$

$\text { RHS }=\tan \theta+\cot \theta \\$

$=\dfrac{\sin \theta}{\cos \theta}+\dfrac{\cos \theta}{\sin \theta} \\$

$=\dfrac{\sin^{2} \theta + \cos^{2} \theta}{\cos \theta \sin \theta} \\$

$=\dfrac{1}{\cos \theta \sin \theta} \\$

$=\operatorname{cosec} \theta \cdot \sec \theta=\text { LHS }$

Hence, proved.

3. The angle of elevation of the top of a tower from a certain point is $30^{\circ}$. If the observer moves $20 \mathrm{~m}$ towards the tower the angle of elevation of the top increases by $15^{\circ}$. Find the height of the tower.

Ans: Consider the height of the vertical tower $ (TW) =x \mathrm{~m}$ (let)

Ist position of the observer at A makes the angle of elevation at the top of the tower is $30^{\circ}$.

Now, the angle of elevation of the top of the tower is increased by $15^{\circ}$, i.e., it becomes $30^{\circ}+15^{\circ}=45^{\circ}$.

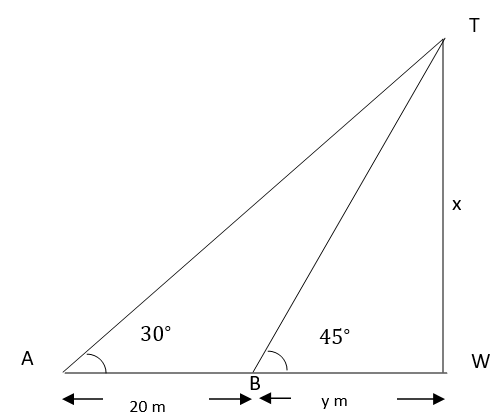
In $\Delta \mathrm{TWB}$, we have

$\tan 45^{\circ}=\dfrac{x}{y} \\$

$\Rightarrow 1=\dfrac{x}{y} \\$

$\Rightarrow \mathrm{x}=\mathrm{y}..................(\mathrm{I})$

Now, $\triangle$ TWA we have

$\tan 30^{\circ}=\dfrac{x}{20+y}$

$\Rightarrow \dfrac{1}{\sqrt{3}}-\dfrac{x}{20+x}[\text { From (I) }] \\$

$\Rightarrow \sqrt{3} x=20+x \\$

$\Rightarrow \sqrt{3} x-x=20 \\$

$\Rightarrow x(\sqrt{3}-1)=20 \\$

$\Rightarrow x=\dfrac{20}{\sqrt{3}-1} \times \dfrac{\sqrt{3}+1}{\sqrt{3}+1} \\$

$\Rightarrow x=\dfrac{20(\sqrt{3}+1)}{3-1} \\$

$\Rightarrow x=\dfrac{20(\sqrt{3}+1)}{2} \\$

$\Rightarrow x=10(1.732+1) \\$

$\Rightarrow x=10 \times 2.732=27.32 \mathrm{~m}$

Hence, the height of the tower is $27.32 \mathrm{~m}$.

4. If $1+\sin ^{2} \theta=3 \sin \theta \cos \theta$, then prove that $\tan \theta=1$, or $\dfrac{1}{2} .$

Ans: To solve an equation in $\theta$, we have to change it into one trigonometric ratio. Given trigonometric equation is

$1+\sin ^{2} \theta=3 \sin \theta \cos \theta \\$

$\Rightarrow \dfrac{1}{\sin ^{2} \theta}+\dfrac{\sin ^{2} \theta}{\sin ^{2} \theta}=\dfrac{3 \sin \theta \cos \theta}{\sin ^{2} \theta} \text { [Dividing by } \sin ^{2} \theta \text { both sides] } \\$

$\Rightarrow \operatorname{cosec}^{2} \theta+1=3 \cot \theta \\$

$\Rightarrow 1+\cot ^{2} \theta+1-3 \cot \theta=0 \\$

$\Rightarrow \cot ^{2} \theta-3 \cot \theta+2=0 \\$

$\Rightarrow \cot ^{2} \theta-2 \cot \theta-1 \cot \theta+2=0 \\$

$\Rightarrow \cot \theta(\cot \theta-2)-1(\cot \theta-2)=0 \\$

$\Rightarrow(\cot \theta-2)(\cot \theta-1)=0 \\$

$\Rightarrow \cot \theta-2=0 \text { Or }(\cot \theta-1)=0 \\$

$\Rightarrow \cot \theta=2 \text { Or } \cot \theta=1$

$\Rightarrow \tan \theta=\dfrac{1}{2} \operatorname{Or} \tan \theta=1$

Hence, $\tan \theta=\dfrac{1}{2}$ or $1$ .

5. Given that $\sin \theta+2 \cos \theta=1$, then prove that $2 \sin \theta-\cos \theta=2$.

Ans: $\sin \theta+2 \cos \theta=1$ [Given]

On squaring both sides, we get

$(\sin \theta)^{2}+(2 \cos \theta)^{2}+2(\sin \theta)(2 \cos \theta)=1 \\$

$\Rightarrow \sin ^{2} \theta+4 \cos ^{2} \theta+4 \sin \theta \cos \theta=1 \\$

$\Rightarrow 1-\cos ^{2} \theta+4\left(1-\sin ^{2} \theta\right)+4 \sin \theta \cos \theta=1 \\$

$\Rightarrow 1-\cos ^{2} \theta+4-4 \sin ^{2} \theta+4 \sin \theta \cos \theta=1 \\$

$\Rightarrow-\cos ^{2} \theta-4 \sin ^{2} \theta+4 \sin \theta \cos \theta=-4 \\$

$\Rightarrow \cos ^{2} \theta+4 \sin ^{2} \theta-4 \sin \theta \cos \theta=4 \\$

$\Rightarrow(\cos \theta)^{2}+(2 \sin \theta)^{2}-2(\cos \theta)(2 \sin \theta)=4 \\$

$\Rightarrow(2 \sin \theta-\cos \theta)^{2}=2^{2}$

Taking square root both sides, we have

$2 \sin \theta-\cos \theta=2$

Hence, proved.

6. The angle of elevation of the top of a tower from two distant points $s$ and $t$ from its foot are complementary. Prove that the height of the tower is $\sqrt{s t}$.

Ans: Let the height of the vertical tower $(TW)=x m$

Points of observation $A$ and $B$ are at distances ' $t$ '" and ' $s$ ' from the foot of the tower.

The angles of elevation of the top of the tower from observation points $A$ and $B$ are $\left(90^{\circ}-\theta\right)$ and $\theta$ which are complementary.

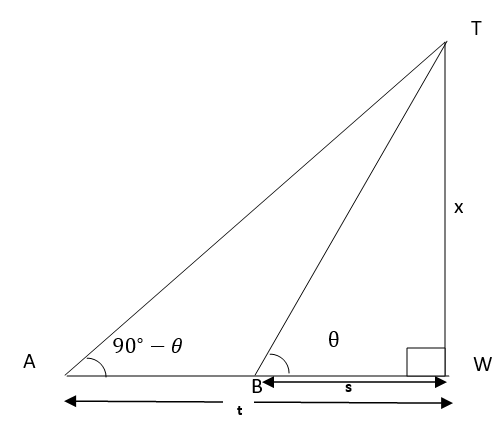
In $\Delta \mathrm{TwB}$, we have

$\tan \theta=\dfrac{x}{s} ………………………….. \text { (i) }$

Now, in $\Delta \mathrm{TWA}$, we have

$\tan \left(90^{\circ}-\theta\right)=\dfrac{x}{t} \\$

$\Rightarrow \cot \theta=\dfrac{x}{t} ……………….. \text { (i) }$

$\Rightarrow \cot \theta \cdot \tan \theta=\dfrac{x}{t} \cdot \dfrac{x}{s}[\text { Multiply eq (1) and (ii) }] \\$

$\Rightarrow \dfrac{1}{\tan \theta} \cdot \tan \theta=\dfrac{x^{2}}{s t} \\$

$\Rightarrow \dfrac{x^{2}}{s t}=1 \\$

$\Rightarrow x^{2}=s t $

$\Rightarrow x=\sqrt{s t}$

Hence proved.

7. The shadow of a tower standing on a plane level is found to be $50 \mathrm{~m}$. longer when the Sun's elevation is $30^{\circ}$ than when it is $60^{\circ}$. Find the height of the tower.

Ans: Let a tower TW of height $x$ (let) is standing vertically upright on a level plane $\mathrm{ABW}$. A And B are two positions of observation when angle of elevation changes from $30^{\circ}$ to $60^{\circ}$ respectively.

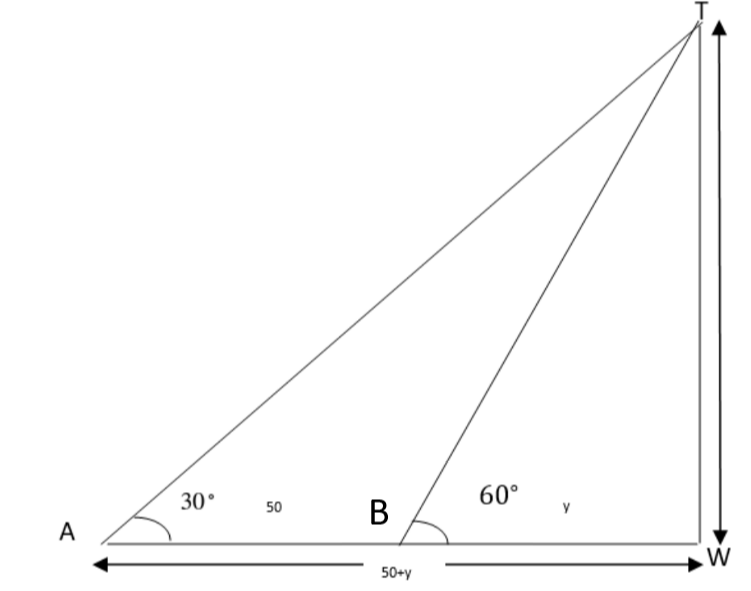
Let $B W=y$ [Given]

$A B=50 \mathrm{~m}$

In $\triangle T W B$, we have

$\tan 60^{\circ}=\dfrac{x}{y} \\$

$\Rightarrow \sqrt{3}=\dfrac{x}{y} \\$

$\Rightarrow x=\sqrt{3} y ……………..(i)$

Now, in $\triangle$ TWA, we have

$\tan 30^{\circ}=\dfrac{x}{y+50} …………..(II)$

$\Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}y}{y+50}    [\text { From (I)] } $

$\Rightarrow 3 y=y+50 \\$

$\Rightarrow 3 y-y=50 \\$

$\Rightarrow 2 y=50 \\$

$\Rightarrow y=25$

Now, $x=\sqrt{3} y$

$\Rightarrow x=\sqrt{3} \times 25 \\$

$\Rightarrow x=25 \sqrt{3} \mathrm{~m}$

8. A vertical tower stands on a horizontal plane and is surmounted by a vertical flag staff of height 'h'. At a point on the plane, the angles of elevation on the bottom and top of the flag staff are $\alpha$ and $\beta$, respectively. Prove that the height of the tower is $\left(\dfrac{h \tan \alpha}{\tan \beta-\tan \alpha}\right)$.

Ans: Let the height of the vertical tower $(T W)=x$.

And, the height of flagstaff (TF)=h (Given)

The angle of elevation at $\mathrm{A}$ on ground from the base and top of the flag staff are $\alpha, \beta$ respectively.

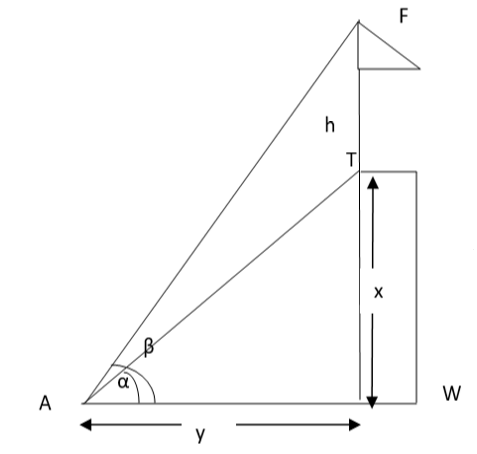
Let $A W=y$

In $\triangle$ TWA, we have

$\tan \alpha=\dfrac{x}{y} \\$

$\Rightarrow \mathrm{y}=\dfrac{x}{\tan \alpha} ………….(\mathrm{I})$

Now, in $\Delta F W A$, we have

$\tan \beta=\dfrac{x+h}{y} \\$

$\Rightarrow y \tan \beta=x+h \\$

$\Rightarrow \dfrac{x \tan \beta}{\tan \alpha}=x+h   [\text { From (I)] }$

$\Rightarrow \mathrm{xtan} \beta=\mathrm{xtan} \alpha+\mathrm{htan} \alpha \\$

$\Rightarrow \mathrm{x}(\tan \beta-\tan \alpha)=h \tan \alpha \\$

$\Rightarrow x=\dfrac{h \tan \alpha}{\tan \beta-\tan \alpha}$

Hence, proved.

9. If $\tan \theta+\sec \theta=l$, then prove that $\sec \theta=\dfrac{l^2+l}{2 l}$.

Ans: [Recall identity $\sec ^{2} \theta-\tan ^{2} \theta=1$ and now change $\sec \theta+\tan \theta$ to $\sec ^{2} \theta-\tan ^{2} \theta$ by multiplying and dividing the given expression to $(\sec \theta-\tan \theta)$.

$\sec \theta+\tan \theta=l \text { [Given] } ………………….(I) $

$\Rightarrow(\sec \theta+\tan \theta) \dfrac{\sec \theta-\tan \theta}{\sec \theta-\tan \theta}=l \\$

$\Rightarrow \dfrac{\sec ^{2} \theta-\tan ^{2} \theta}{\sec \theta-\tan \theta}=l\left[\because 1+\tan ^{2} \theta=\sec ^{2} \theta\right] \\$

$\Rightarrow \dfrac{1}{\sec \theta-\tan \theta}=l \\$

$\operatorname{or} \sec \theta-\tan \theta=\dfrac{1}{l}..................(II)$

Now, get $\sec \theta$ by eliminating $\tan \theta$ from (I) and (II). It can be obtained by adding (I) and (II).

$\Rightarrow 2 \sec \theta=l+\dfrac{1}{l} \\$

$\Rightarrow 2 \sec \theta=\dfrac{l^{2}+1}{l} \\$

$\Rightarrow \sec \theta=\dfrac{l^{2}+1}{2 l}$

Hence, proved.

10. If $\sin \theta+\cos \theta=p$ and $\sec \theta+\operatorname{cosec} \theta=q$, then prove that $q\left(p^{2}-1\right)=2 p$.

Ans: $\sin \theta+\cos \theta=p$------------(I)

$\sec \theta+\operatorname{cosec} \theta=q$

IInd expression can be changed into $\sin \theta, \cos \theta$ and eliminate trigonometric ratio from (I) and (II)

$\sec \theta+\operatorname{cosec} \theta=q$

$\Rightarrow \dfrac{1}{\cos \theta}+\dfrac{1}{\sin \theta}=q \\$

$\Rightarrow \dfrac{\sin \theta+\cos \theta}{\cos \theta \sin \theta}=\dfrac{q}{1} \\$

$\Rightarrow \dfrac{p}{\sin \theta \cos \theta}=q --------------[\text { Using (I) }] \\$

$\Rightarrow \sin \theta \cos \theta=\dfrac{p}{q} -------------\text { (II) } \\$

$\sin \theta+\cos \theta=p[\text { From (I) }] \\$

$\Rightarrow(\sin \theta+\cos \theta)^{2}=p^{2}[\text { Squaring both sides }] \\$

$\Rightarrow \sin ^{2} \theta+\cos ^{2} \theta+2 \sin \theta \cos \theta=p^{2} \\$

$\Rightarrow 1+2 \dfrac{p}{q}=p^{2}\left[\because \sin ^{2} \theta+\cos ^{2} \theta-1\right. \text { And using (II) } \\$

$\Rightarrow q+2p=p^{2} q \\$

$\Rightarrow 2p=p^{2} q-q \\$

$\Rightarrow 2p=q\left(p^{2}-1\right)$

Hence, proved.

11. If $a \sin \theta+b \cos \theta=c$, then prove that $a \cos \theta-b \sin \theta=\sqrt{a^{2}+b^{2}-c^{2}}$.

Ans: $a \sin \theta+b \cos \theta=c$ [Given]

On squaring both sides, we get

$(a \sin \theta)^{2}+(b \cos \theta)^{2}+2(a \sin \theta)(b \cos \theta)=c^{2} $

$\Rightarrow  a^{2} \sin ^{2} \theta+b^{2} \cos ^{2} \theta+2 a b \sin \theta \cos \theta=c^{2} \\$

$\Rightarrow  a^{2}\left(1-\cos ^{2} \theta\right)+b^{2}\left(1-\sin ^{2} \theta\right)+2 a b \sin \theta \cos \theta=c^{2} \\$

$\Rightarrow  a^{2}-a^{2} \cos ^{2} \theta+b^{2}-b^{2} \sin ^{2} \theta+2 a b \sin \theta \cos \theta=c^{2} \\$

$\Rightarrow -a^{2} \cos ^{2} \theta-b^{2} \sin ^{2} \theta+2 a b \sin \theta \cos \theta=c^{2}-a^{2}-b^{2} \\$

$\Rightarrow  a^{2} \cos ^{2} \theta+b^{2} \sin ^{2} \theta-2 a b \sin \theta \cos \theta=a^{2}+b^{2}-c^{2}$

$\Rightarrow(a \cos \theta)^{2}+(b \sin \theta)^{2}-2(a \cos \theta)(b \sin \theta)=a^{2}+b^{2}-c^{2} \\$

$\Rightarrow(a \cos \theta-b \sin \theta)^{2}=a^{2}+b^{2}-c^{2}$

$\Rightarrow a \cos \theta-b \sin \theta= \pm \sqrt{a^{2}+b^{2}-c^{2}} \text { (Taking square root both sides) }$

Hence, $a \cos \theta-b \sin \theta= \pm \sqrt{a^{2}+b^{2}-c^{2}}$

Hence proved.

12. Prove that $\dfrac{1+\sec \theta-\tan \theta}{1+\sec \theta+\tan \theta}=\dfrac{1-\sin \theta}{\cos \theta}$

Ans: Recall identity $\sec ^{2} \theta=\tan ^{2} \theta+1$

$\text { LHS }=\dfrac{1+\sec \theta-\tan \theta}{1+\sec \theta+\tan \theta} \\$

$=\dfrac{\sec ^{2} \theta-\tan ^{2} \theta+\sec \theta-\tan \theta}{1+\sec \theta+\tan \theta} \\$

$=\dfrac{(\sec \theta-\tan \theta)(\sec \theta+\tan \theta)+(\sec \theta-\tan \theta)}{1+\sec \theta+\tan \theta}\left[\because \mathrm{a}^{2}-\mathrm{b}^{2}=(\mathrm{a}-\mathrm{b})(\mathrm{a}+\mathrm{b})\right] \\$

$=\dfrac{(\sec \theta-\tan \theta)[1+\sec \theta+\tan \theta]}{1+\sec \theta+\tan \theta} \\$

$={\sec \theta-\tan \theta}\\$

$={\dfrac{1}{\cos \theta}-\dfrac{\sin \theta}{\cos \theta}} \\$

$=\dfrac{1-\sin \theta}{\cos \theta}=R H S\\$

Hence, proved.

13. The angle of elevation of the top of a tower $30 \mathrm{~m}$ high from the foot of another tower in the same plane is $60^{\circ}$ and the angle of elevation of the top of second tower from the foot of first tower is $30^{\circ}$. Find the distance between the two towers and also the height of the other tower.

Ans: Two vertical tower $T W=30 \mathrm{~m}$ and $ER = x \mathrm{~m}$ (let) are standing on a horizontal plane $\mathrm{RW}=\mathrm{y}$ (let). The angle of elevation from $\mathrm{R}$ to top $30 \mathrm{~m}$ high tower is $60^{\circ}$ and the angle of elevation of second tower from $\mathrm{W}$ is $30^{\circ}$.

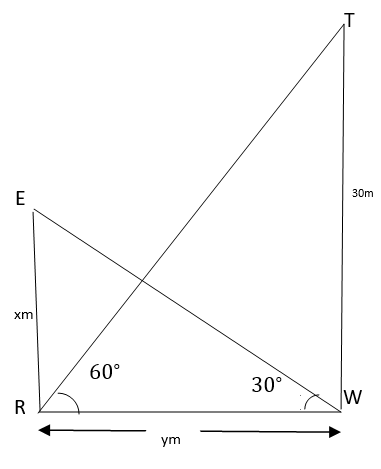
In $\triangle B R W$,

$\tan 30^{\circ}=\dfrac{x}{y} \\$

$\Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{x}{y} \\$

$\Rightarrow y=\sqrt{3} x …………………..\text { (I) }$

Now, In $\triangle T W R$,

$\tan 60^{\circ}=\dfrac{30}{y} \\$

$\Rightarrow \sqrt{3}=\dfrac{30}{\sqrt{3} x} \quad[\text { From (I)] } \\$

$\Rightarrow 3 x=30 \\$

$\Rightarrow x=10 \mathrm{~m}$

$\text { Now, } y=\sqrt{3} x \\$

$\Rightarrow y=\sqrt{3}(10) \\$

$\Rightarrow y=1.732 \times 10 \\$

$\Rightarrow y=17.32 \mathrm{~m}$

Hence, the distance between the two towers is $17.32 \mathrm{~m}$ and the height of the second tower is $10 \mathrm{~m}$.

14. From the top of a tower $\mathrm{h} \mathrm{~m}$ high, the angles of depression of two objects, which are in line with the foot of the tower are $\alpha$ and $\beta,(\beta>\alpha)$. Find the distance between the two objects.

Ans: Consider a vertical tower $T W=h\mathrm{~m}$. Two objects $A$ and $B$ are $x \mathrm{~m}$ apart in the line joining $A, B$ and $W$ and $B W=y$ (let).

The angle of depression from top of a tower to objects $A$ and $B$ are $\alpha$ and $\beta$ respectively.

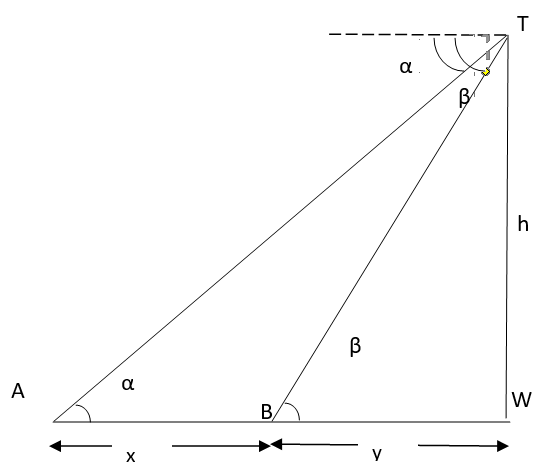
 In $\triangle T W B$, we have

$\tan \beta=\dfrac{h}{y} \\$

$\Rightarrow y=\dfrac{h}{\tan \beta} ……………..\text { (I) }$

Now, in $\triangle$ TWA,

$\tan \alpha=\dfrac{h}{x+y} \\$

$\Rightarrow \tan \alpha(\mathrm{x}+\mathrm{y})=\mathrm{h} \\$

$\Rightarrow\left(x+\dfrac{h}{\tan \beta}\right) \tan \alpha=\mathrm{h}[\text { From (I) }] \\$

$\Rightarrow \mathrm{xtan} \alpha+\dfrac{h \tan \alpha}{\tan \beta}=\mathrm{h} \\$

$\Rightarrow \mathrm{xtan} \alpha=\mathrm{h}-\dfrac{h \tan \alpha}{\tan \beta} \\$

$\Rightarrow \mathrm{x} \tan \alpha=\dfrac{h \tan \beta-h \tan \alpha}{\tan \beta} \\$

$\Rightarrow \mathrm{x}=h\left[\dfrac{\tan \beta-\tan \alpha}{\tan \alpha \cdot \tan \beta}\right] \\$

$\Rightarrow \mathrm{x}=h\left[\dfrac{\tan \beta}{\tan \alpha \cdot \tan \beta}-\dfrac{\tan \alpha}{\tan \alpha \cdot \tan \beta}\right] \\$

$\Rightarrow \mathrm{x}=h\left[\dfrac{1}{\tan \alpha}-\dfrac{1}{\tan \beta}\right] \\$

$\Rightarrow \mathrm{x}=\mathrm{h}[\cot \alpha-\cot \beta]$

Hence, the distance between the two objects is $\mathrm{h}(\cot \alpha-\cot \beta) \mathrm{m}$.

15. A ladder rests against a vertical wall at an inclination $\alpha$ to the horizontal. Its foot is pulled away from the wall through a distance $p$, so that its upper end slides a distance q down the wall and then the ladder makes an angle $\beta$ with horizontal. Show that $\dfrac{p}{q}=\dfrac{\cot \beta-\cos \alpha}{\sin \alpha-\sin \beta}$.

Ans: Consider a vertical wall WB. Two positions AW and ID of a ladder as shown

in the figure such that $L A=p, W D=q$ and $L D=A W=z$. The angle of inclination of the ladder at two positions $A$ and $L$ are $\alpha$ and $\beta$ respectively.

Let $A B=y$ and $D B=x$.

In $\triangle A B W$, we have

$\sin \alpha=\dfrac{x+q}{z}$

and $\cos \alpha=\dfrac{y}{z}$

In $\triangle \mathrm{LBD}$, we have

$\sin \beta=\dfrac{x}{z}$ 

and $\cos \beta=\dfrac{y+p}{z}$

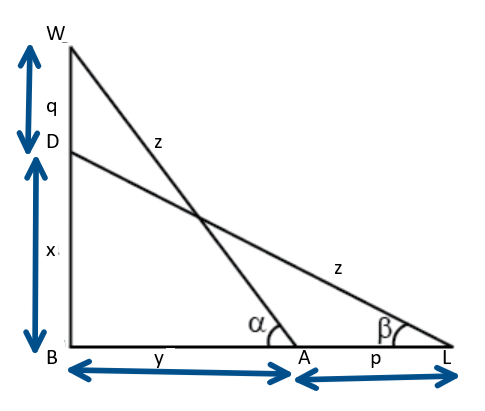
Taking RHS $=\dfrac{\cot \beta-\cos \alpha}{\sin \alpha-\sin \beta}$

$=\dfrac{\dfrac{y+p}{z}-\dfrac{y}{z}}{\dfrac{x+q}{z}-\dfrac{x}{z}}  =\dfrac{\dfrac{y+p-y}{z}}{\dfrac{x+q-x}{x}} \\$

$=\dfrac{p}{q}\\$

$\text { =LHS }$

Hence proved.

16. The angle of elevation of the top of a vertical tower from a point on the ground is $60^{\circ}.$ From another point $10 \mathrm{~m}$ vertically above the first, its angle of elevation is $45^{\circ}$. Find the height of the tower.

Ans: Let the height of the vertical tower $T W=x \mathrm{~m}$.

It stands on a horizontal plane $AW=\mathrm{y}$.

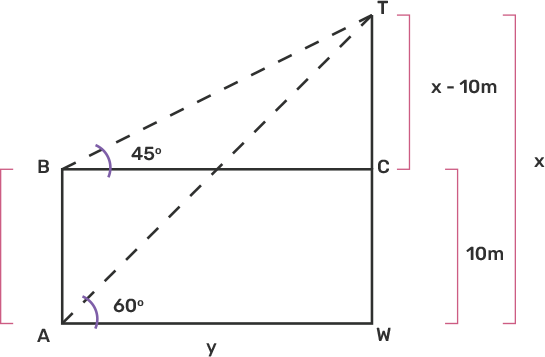
Also $\mathrm{BC}=\mathrm{y}$

Observation point $B$ is $10 \mathrm{~m}$ above the first observation point $A$.

The angles of elevation from point of observations A and $B$ are $60^{\circ}$ and $45^{\circ} \mathrm{m}$ respectively.

$T C=x-10$

In right-angled triangle $\mathrm{TBC}$, we have

$\tan 45^{\circ}=\dfrac{x-10}{y} $

$\Rightarrow 1=\dfrac{x-10}{y} \\$

$\Rightarrow y=x-10 …………..(I)$

Now, in $\triangle \mathrm{TAW}$,

$\tan 60^{\circ}=\dfrac{x}{y} \\$

$\Rightarrow \sqrt{3}=\dfrac{x}{x-10}[\text { From (I) }] \\$

$\Rightarrow \sqrt{3} x-10 \sqrt{3}=x \\$

$\Rightarrow \sqrt{3} x-x=10 \sqrt{3} \\$

$\Rightarrow x(\sqrt{3}-1)=10 \sqrt{3} \\$

$\Rightarrow x=\dfrac{10 \sqrt{3}}{(\sqrt{3}-1)} \times \dfrac{(\sqrt{3}+1)}{(\sqrt{3}+1)} \\$

$\Rightarrow x=\dfrac{10(\sqrt{3}+3)}{(\sqrt{3})^{2}-1} \\$

$\Rightarrow x=\dfrac{10 \times(3+1.732)}{3-1} \\$

$\Rightarrow x=\dfrac{10 \times 4.732}{2} \\$

$\Rightarrow x=10 \times 2.366 \\$

$\Rightarrow x=23.66 \mathrm{~m}$

Hence, the height of the tower is $23.66 \mathrm{~m}$.

17. A window of a house is $\mathrm{h} \mathrm{~m}$ above the ground. From the window, the angles of elevation and depression of the top and the bottom of another house situated on the opposite side of the lane are found to be $\alpha$ and $\beta$ respectively.

Prove that the height of the other house is $h(1+\tan \alpha \cot \beta) m$.

Ans: Window $\mathrm{w}, \mathrm{h} \mathrm{~m}$ above the ground point $\mathrm{A}$, another house HS $=\mathrm{x}(\mathrm{m}), \mathrm{AS}=\mathrm{y}(\mathrm{m})$ away from observation window, $A S=W N=y$ (let) $N S=h, H =(x-h)$.

Angle of elevation and depression of top and bottom of house HS from window W are. $\alpha, \beta$ respectively.

In right angled $\Delta  WNS$,

$\tan \beta=\dfrac{h}{y} \\$

$\Rightarrow \mathrm{y}=\dfrac{h}{\tan \beta} ………….\text { (I) }$

Now, in right angled $\Delta H N W$,

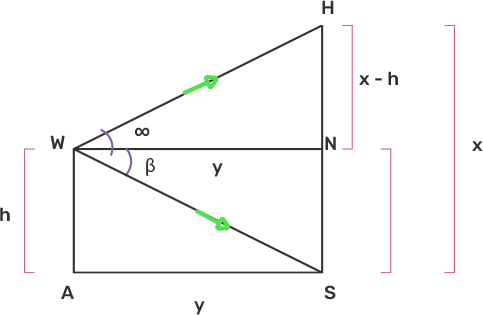
$\Rightarrow \tan \alpha=\dfrac{x-h}{y}$ 

$\Rightarrow y \tan \alpha=x-\operatorname{h}$ 

$\Rightarrow \dfrac{h \tan \alpha}{\tan \beta}=x-h[F r o m(I)]$ 

$\Rightarrow h \tan \alpha=x \tan \beta-h \tan \beta$ 

$\Rightarrow x=\dfrac{h(\tan \alpha+\tan \beta)}{\tan \beta}$ 

$\Rightarrow x=h\left(\dfrac{\tan \alpha}{\tan \beta}+\dfrac{\tan \beta}{\tan \beta}\right)$ 

$\Rightarrow x=h[\tan \alpha \cot\beta+1]$ 

Hence, the height of the house on the other side of the observer is $h[1+\tan \alpha \cdot \cot \beta] \mathrm{m} .$

18. The lower window of a house is at a height of $2 \mathrm{~m}$ above the ground and its upper window is $4 \mathrm{~m}$ vertically above the lower window. At certain instant the angles of elevation of a balloon from these windows are observed to be $60^{\circ}$ and $30^{\circ}$, respectively. Find the height of the balloon above the ground.

Ans: Let $B$ be a balloon at a height $G B=x \mathrm{~m}$.

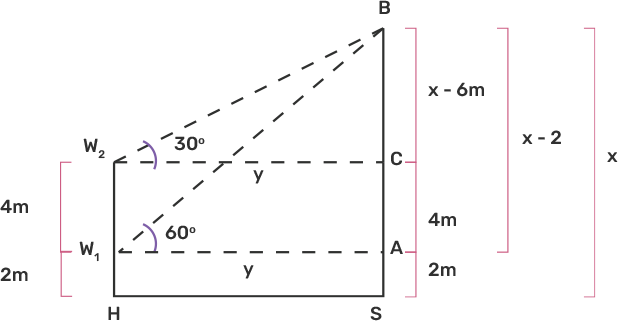
Let the window, which is $2 \mathrm{~m}$ above the ground $\mathrm{H}$.

$\therefore \mathrm{W}_{1} \mathrm{H}=2$ 

$\Rightarrow \mathrm{AG}=2 \mathrm{~m}$

Let $\mathrm{W}_{2}$ be the second window, which is the $4 \mathrm{~m}$ above the window $\mathrm{W}_{1}$.

$\therefore \mathrm{W}_{2} \mathrm{~W}_{1}=\mathrm{AC}=4 \mathrm{~m}$

The angles of elevation of balloon B from $\mathrm{W}_{1}, \mathrm{W}_{2}$ are $60^{\circ}$ and $30^{\circ}$ respectively.

$B A=(x-2) m$

$\mathrm{BC}=\mathrm{x}-2-4=(\mathrm{x}-6) \mathrm{m}$

In right angled $\Delta \mathrm{W}_{2} \mathrm{CB}$, we have

$\tan 30^{\circ}=\dfrac{x-6}{y} \\$

$\Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{x-6}{y} \\$

$\Rightarrow y=\sqrt{3}(x-6).....................(I)$

Now, in right-angled $\Delta {W_{1}}AB$

$\tan 60^{\circ}=\dfrac{x-2}{y} \\$

$\Rightarrow \sqrt{3}=\dfrac{x-2}{y} \\$

$\Rightarrow \sqrt{3} y=(x-2) …………………\text { (II) } \\$

$\Rightarrow \sqrt{3} \cdot \sqrt{3}(x-6)=x-2[\text { From (I) }] \\$

$\Rightarrow 3 x-18=x-2 \\$

$\Rightarrow 3 x-x=18-2 \\$

$\Rightarrow 2 x=16 \\$

$\Rightarrow x=8 m$

Hence, the height of the balloon above the ground is $8 \mathrm{~m}$.

Trigonometry

The most common and important tool in mathematics is trigonometry. It is the core subject and the first topic of secondary school for the students to learn mathematics. It is known as the study of three-dimensional angles. The concept of the unit circle is also a part of trigonometry. The basic definition of trigonometry is a kind of mathematics that deals with the trigonometric properties of an angle. It helps the student to understand the relationships between the angles, a point, and a line and their relations. A right-angled triangle is the most common type of triangle in trigonometry. Another important concept in trigonometry is the basic law which is known as sine law. It states that all the signs of an angle are equal in value. 

Understanding Trigonometry

To have a better understanding of the concept of sine, students are taught the concept of a tangent. The equation is the general form of a trigonometric function, namely the Sine Law and the Pythagorean Theorem. These basic mathematical equations are used to find the different trigonometric functions. As the students advance in their studies, they are taught the different types of trigonometric functions like the functions of angles, the functions of sides, and angle measure.

Significance of Trigonometric Functions

The trigonometric functions are the most widely used in all the areas of mathematics and scientific aspects. This is the basic and the most common definition of Trigonometry. The different types of trigonometric functions are the functions of angles, the functions of sides, and angle measure. For the past two centuries, trigonometric functions have been the main subjects of mathematics. It is the foundation of algebra and geometry. It is also known as the study of geometric angles, the angle measure, and also the study of triangles.

Trigonometry in Elementary School

In elementary school and at the same time in secondary schools, trigonometry is the first course studied. The students learn with the different types of trigonometric functions like the functions of angles, the functions of sides, and angle measure. At the same time, in primary school, students are taught with the use of a ruler and compass. This helps in the measuring of the angle and also helps in the calculation of the angle measure.

Trigonometry in Secondary School

After the completion of elementary school, trigonometry is introduced in secondary schools. There are many ways in which trigonometric functions are learned and also discussed. Some of the other topics discussed in trigonometry include the trigonometric functions, the functions of angles, the functions of sides and angle measure, the study of triangles, and also the Pythagorean Theorem. The two most important trigonometric functions are sine law and the Pythagorean Theorem. They are learned with the help of the ruler and the compass.

Trigonometry and its Equation

Trigonometry is the science of triangles that deals with the properties of right-angled triangles. A triangle is a geometrical construction, where one of the three angles has been given a special name - acute, obtuse, or right. The acute angle is one where the measure is less than 90°. The obtuse angle is one where the measure is greater than 90°. The third angle is then called right. The acute and obtuse angles are both called angles. The right angle is called a vertex. If one angle is 90°, then the triangle is called a right-angled triangle.

What does Triginimetry deal with?

Trigonometry deals with the three types of triangles known as right-angled, obtuse, and acute triangles. Trigonometry describes these triangles and studies the relationships between them. It also describes the relationship between angles and sides of a triangle. It explores the relationships of sin, cosine, tangent, tangent, cotangent, secant, cosecant, cosecant, and secant. There are also other trigonometric functions, such as hyperbolic functions like CSC (cosine of an angle), cotc (cotangent of an angle), and csch (sine hyperbolic).

Free PDF download of NCERT Exemplar for Class 10 Maths Chapter 8

Free PDF download of NCERT Exemplar for Class 10 Maths Chapter 8 - Introduction to Trigonometry & Its Equation solved by expert Maths teachers on Vedantu.com as per NCERT (CBSE) Book guidelines. All Chapter 8 - Introduction to Trigonometry & Its Equation exercise questions with solutions to help you to revise the complete syllabus and score more marks in your examinations. You can also download Class 10 Maths NCERT Solutions to help you revise the complete syllabus and score more marks in your examination. Vedantu is a platform that provides free NCERT Solutions and other study materials for students. Subjects like Science, Maths, English will become easy to study if you have access to NCERT Solution for Class 10 Science, Maths solutions, and solutions of other subjects that are available on Vedantu only.