Master Class 10 Arithmetic Progressions Exercise 5.3 Solutions with Expert Guidance
NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions
FAQs on NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions
1. How are stepwise NCERT Solutions for Class 10 Maths Chapter 5 Exercise 5.1 provided in the CBSE-approved answer format?
The stepwise NCERT Solutions for Class 10 Maths Chapter 5 Exercise 5.1 are structured strictly as per the CBSE 2025–26 NCERT answer format. Each question is solved systematically, highlighting which formula or property of arithmetic progression (AP) is used in each step. Answers begin with what is given, clearly state what needs to be found (such as the nth term, sum of n terms, common difference, or verification of an AP), and follow through using the correct formulae like an = a + (n-1)d or Sn = n/2[2a + (n-1)d]. Units, reasoning, and working are all shown for full marks as per CBSE guidance.
2. Where can I find the official NCERT solution PDF for Class 10 Maths Chapter 5 (Arithmetic Progressions), including Hindi medium?
The official NCERT solution PDF for Class 10 Maths Chapter 5, including solutions in both English and Hindi medium (NCERT solutions for class 10 maths chapter 5 in hindi pdf), is available for direct download on trusted educational portals like Vedantu and on the NCERT’s official website. These PDFs provide CBSE-approved, chapter-wise, and exercise-wise solutions for all questions under Arithmetic Progressions, including Exercises 5.1, 5.2, and 5.3, presented with stepwise explanations according to the current NCERT syllabus.
3. How do you solve NCERT Class 10 Maths Chapter 5 Exercise 5.2 using the official NCERT pattern?
To solve NCERT Class 10 Maths Chapter 5 Exercise 5.2 as per the official NCERT/CBSE pattern, always begin by stating the information given in the question such as first term (a), common difference (d), and the term number (n) or sum required. Apply relevant formulae (an = a + (n-1)d for nth term, or Sn = n/2 [2a + (n-1)d] for sum), substitute the given values, and perform calculations stepwise. All reasoning, calculations, and final answers are written in alignment with the CBSE marking guidelines for 2025–26.
4. Are the NCERT Solutions for Class 10 Maths Chapter 5 (Tiwari Academy, Teachoo, Vedantu) aligned with the latest CBSE syllabus for 2025–26?
Yes, the NCERT Solutions for Class 10 Maths Chapter 5 available on platforms like Tiwari Academy, Teachoo, and Vedantu are updated and fully aligned with the latest CBSE 2025–26 syllabus. They follow the official NCERT textbook structure, provide stepwise solutions, and ensure that each answer matches the required NCERT/CBSE answer format for Arithmetic Progressions. Always check if your study material mentions the current academic year and follows the updated exercise numbering as per the NCERT 2025–26 curriculum.
5. What is the correct stepwise method to check if a given sequence is an AP, as explained in Class 10 Maths Chapter 5?
To check if a sequence is an AP (Arithmetic Progression), list the sequence’s terms and calculate the difference between each successive pair (i.e., subtract each term from the next). If this difference (d) remains constant throughout, it is an AP. This method follows the NCERT answer format where solutions clearly show every step and explicitly state whether the given sequence meets the requirement for an AP, as per the CBSE 2025–26 guidelines.
6. What formulas must be used for solving sum and nth term questions from Class 10 Maths Chapter 5 Arithmetic Progressions?
For Class 10 Maths Chapter 5 Arithmetic Progressions, always use the standard NCERT formulas: the nth term is given by an = a + (n-1)d, and the sum of n terms by Sn = n/2 [2a + (n-1)d] or Sn = n/2 (a + l), where ‘l’ is the last term. The NCERT solutions demonstrate which formula to use stepwise, with proper substitution and final answer as per CBSE-approved solving pattern.
7. What is the AP in Class 10 NCERT Maths and how are problems from Exercise 5.3 generally approached?
In Class 10 NCERT Maths, an Arithmetic Progression (AP) is a sequence in which the difference between any two consecutive terms is constant. In Exercise 5.3, problems usually involve real-life applications based on AP – such as total distance covered, finding which term is a particular value, or calculating the sum of selected terms. Each solution in the NCERT answer format starts with identifying a, d, n (if not given, deduced from question data) and then uses an and Sn formulas appropriately, following a stepwise approach.
8. Can I get NCERT Solutions for Class 10 Maths Chapter 5 in Hindi medium with correct CBSE format?
Yes, NCERT Solutions for Class 10 Maths Chapter 5 in Hindi medium (गणित अध्याय 5 गणितीय प्रगति – कक्षा 10 हल) are available in correct CBSE answer format. These Hindi medium solutions are provided for each exercise (5.1, 5.2, 5.3) with detailed and stepwise NCERT style explanations, strictly adhering to the latest syllabus and question pattern for Hindi medium students.
9. How to solve arithmetic progression questions in Class 10 Maths using NCERT and CBSE-approved methods?
To solve arithmetic progression questions in Class 10 Maths using NCERT and CBSE-approved methods, always begin by extracting given data, identifying first term (a) and common difference (d), and determine whether you should find a specific term or the sum of terms. Use the formula for nth term or sum (as provided in the NCERT solutions) and ensure all calculations are presented clearly in a stepwise manner, matching the NCERT pattern. Complete each part of the question, show substitution, and box the final answer as per board guidelines.
10. Is the Class 10 Maths exam easy if one prepares using official NCERT Solutions for Chapter 5?
The CBSE Class 10 Mathematics paper is considered moderate in difficulty, but becomes approachable and manageable if you prepare systematically with official NCERT Solutions, especially for Chapter 5 (Arithmetic Progression). The solutions follow the exact syllabus, previous year question trends, and stepwise problem-solving expected by CBSE, making exam questions directly approachable if the NCERT answer writing pattern is practiced regularly.
11. FUQ: Why do students make calculation errors in AP sum or nth term questions and how does NCERT format help?
Calculation errors in AP questions often occur due to incorrect substitution in formulas or missing steps. Following the NCERT solution format, each calculation is written explicitly step by step – value recognition, substitution, arithmetic operation, and final answer – which ensures accuracy and easier verification. This systematic approach as illustrated in NCERT solutions helps minimize mistakes in AP sum and nth term problems, especially during exams.
12. FUQ: What is the importance of ‘stepwise explanation’ in scoring full marks in NCERT Class 10 Maths Chapter 5 Arithmetic Progressions?
Stepwise explanation is crucial in Class 10 Maths Chapter 5, as CBSE awards marks for each correct step shown. By following the NCERT answer format, every calculation or reasoning is written out, ensuring that even partial work gets marks and the full solution is traceable for the examiner. Stepwise answers are especially important in AP, where multi-step calculations are involved, thus boosting your score as per CBSE marking scheme.
13. FUQ: If the common difference is negative or zero, can it still be an AP in NCERT Class 10?
Yes, as per NCERT and CBSE guidelines in Class 10 Maths, an AP can have a common difference (d) that is positive, negative, or zero. The defining criterion is that the difference between consecutive terms remains constant. NCERT solution steps always include calculation of common difference and verification of its constancy, regardless of its sign.
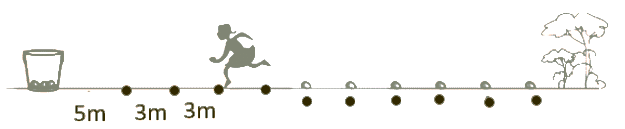
14. FUQ: How are word problems in Exercise 5.3 (like finding terms from life situations) solved in NCERT solutions?
In NCERT solutions for Exercise 5.3, word problems are broken down by first interpreting the context into mathematical data (identifying a, d, n), then applying AP formulas as per question requirement. All wording is translated stepwise into equations or known variables, and solved using the standard NCERT/CBSE-approved style to ensure conceptual clarity and scoring full marks.




















 Watch Video
Watch Video