Lines and Pair of Lines - Introduction
You've probably seen a train line game, a ladder game, or a piano key game. Is there anything any of these have in common? The two sides of the ladder never touch, and the two tracks never cross. At all times, the piano keys are parallel to one another. These are all parallel lines examples.
Any line is made up of points, which is the minimum unit. A point, said Euclid, is that which has no dimension: neither high, nor wide, nor deep. So, those dots can only live in the imagination of the mathematician because they are infinitely small. Parallel lines are in the same plane and maintain a certain distance from each other, but they never cross, approach or touch at any point, not even their extensions. Intersecting lines intersect at a point. When cut, they divide the plane into 4 regions, which is why we say they form 4 angles.
What are Parallel Lines?
Parallel lines are two lines that never cross and retain their distance even when extended to infinity. The characteristic of parallel lines, also known as equidistant lines, is that they never touch and always point in the same direction.
In Mathematics, it is important to differentiate pair of parallel lines from perpendicular lines. Parallel lines, as their name indicates, are parallel; therefore, they accompany each other throughout the trajectory but without touching. Perpendicular lines, on the other hand, are only close together at the point where they intersect, creating a 90-degree angle.
Transversal Lines
When parallel lines are crossed by a straight line, pairs of equal angles are formed, called, for this reason, pairs of angles.
The line that crosses the parallel lines is called a transversal line and is characterised by creating two parallel or equidistant lines with angles that have the same number of degrees.
Angle pairs are important in checking whether two lines are indeed parallel. To check whether they are parallel or equidistant, the following conditions must be met:
Corresponding angles are equal.
Alternate interior angles are equal.
Consecutive interior angles are equal.
Consecutive interior angles add up to 180 degrees.
Characteristics of a Pair of Intersecting Lines
They have an intersection point.
They can be oblique or perpendicular.
When intersecting lines intersect, regions known as angles are formed.
They are not kept equidistantly.
Parallel and Transversal lines
Let's take a closer look at parallel and transversal lines and their corresponding angles.
Parallel lines: The combination of two or more lines that stretch to infinity and never cross each other are called parallel lines or coplanar lines. An exclusive symbol, denoted by ||, denotes parallel lines.
Corresponding Angles: The angles formed when a transversal intersects any two parallel lines are called corresponding angles.
The following figure shows parallel and transversal lines along with the corresponding angles formed by them as
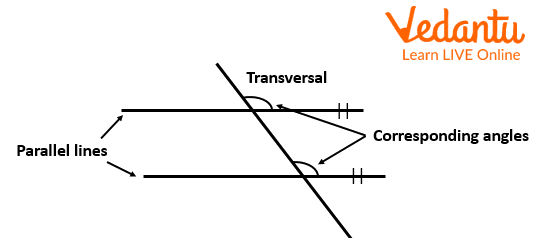
Pairs of lines
Facts and Characteristics of Transversal and Parallel Lines
There are eight angles created when two parallel lines a transversal line cross two parallel lines. These angles all have a few characteristics described below:
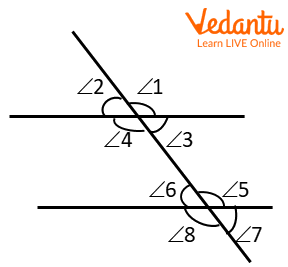
Transversal line
1. The pair of corresponding angles are equal.
Example: \[\angle 1 = \angle 5,\angle 4 = \angle 8\]
2. The alternate interior angles are equal.
Example: \[\angle 4 = \angle 5\]
3. The pair of alternate exterior angles are equal.
Example: \[\angle 1 = \angle 8\]
4. The co-interior angles are supplementary angles.
Example: \[\angle 4 + \angle 6 = {180^\circ }\]
5. The co-exterior angles are supplementary angles.
Example: \[\angle 2 + \angle 8 = {180^\circ }\]
6. Vertically opposite angles are equal.
Example: \[\angle 5 = \angle 8\].
Solved Examples
Example 1:
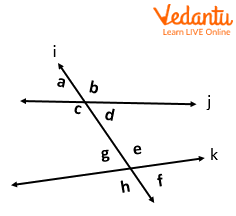
Intersecting lines and transversal
The transversal l in the given diagram cuts the lines j and k. The angles ∠c and ∠e are…
A. Corresponding Angles
B. Consecutive Interior Angles
C. Alternate Interior Angles
D. Alternate Exterior Angles
Sol: The angles ∠c and ∠e lie on either side of the transversal l and inside the two lines j and k.
Therefore, they are alternate interior angles.
The correct choice is C.
Example 2:
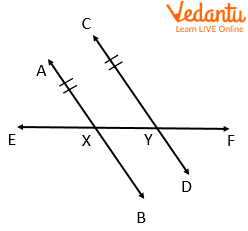
Parallel and transversal line
In the above figure, if lines AB and CD are parallel and m∠AXF=140°, then what is the measure of ∠CYE?
Sol: The angles ∠AXF and ∠CYE lie on one side of the transversal EF and inside the two lines AB and CD. So, they are consecutive interior angles.
Since the lines AB and CD are parallel, by the consecutive interior angle’s theorem, ∠AXF and ∠CYE are supplementary.
That is, m∠AXF+m∠CYE=180°
But, m∠AXF=140°
Substitute and solve
140°+m∠CYE=180°
140°+m∠CYE−140°=180°−140°
m∠CYE=40°
Key Features
We refer to the location at which two lines intersect as the point of intersection.
We refer to lines that are created on a piece of paper that does not meet, regardless of how far apart they are, as parallel lines.
We have two pairs of opposing angles when two lines intersect, forming the letter X. The term "vertically opposite angles" describes them. They are equal in measure.
A line that crosses two or more other lines at different locations is said to be transversal.
Several different angles can be created from a transversal.
List of Related Articles
Practice Questions
Q 1: Write the name of the lines in the given figure.
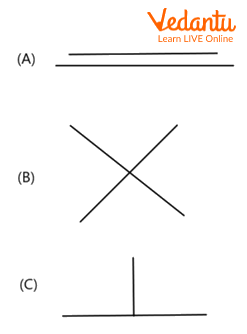
Type of lines (parallel, intersecting and perpendicular)
Sol:
A pair of parallel lines is Option A.
A pair of intersecting or non-parallel lines is option B.
An example of perpendicular lines is in Option C.
Q 2: Tom is picking the points of intersection of the lines given in the figure below, he observed that there are 5 points of intersection. Is he right?
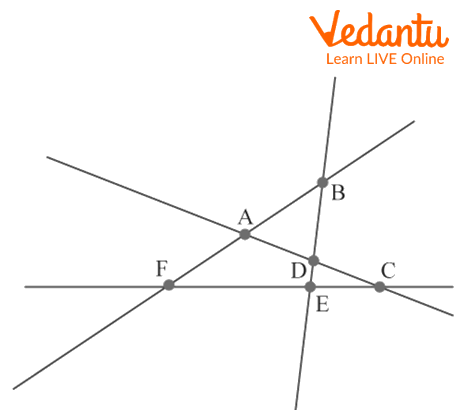
Intersecting lines
Sol: The points at which any of these lines are intersecting are: A, B, C, D, E, F.
Hence there are a total 6 intersection points.
FAQs on Pairs of Lines
1: What is a transversal line?
Any line that crosses two or more other lines at different locations is said to be transversal. Various sorts of angles in pairs, including successive internal angles, corresponding angles, and alternate angles, are produced by a transversal intersection with two lines.
2: What angles are formed when an intersecting line cuts two parallel lines?
Each pair of internal angles on the same side of a transversal that intersects two parallel lines is supplementary, or they add up to 180°. The opposite angles created by the intersecting lines are known as vertical angles or vertically opposite angles. The intersecting lines cut each other at a point.
3: Are straight transversal lines possible?
Transversals are straight lines crossing two or more other lines at distinct points. When a transversal line crosses another line, four angles are created around the intersection.