What Are Parallel Lines Definition Properties and Angle Relationships
Parallel lines are straight lines that are equidistant from each other and have the same slope. So, when two or more lines do not meet at any point, we call them parallel.
Just observe the section-wise lines of each class during the morning assembly, you notice that these lines are at some distance from each other and they don’t meet at any point. This arrangement shows that lines are parallel, also, these lines meet at nowhere or infinity.
So, what other characteristics do parallel lines hold? Also, how do we categorise the properties of lines with the help of transversal lines, we will understand all about it in detail.
Parallel Lines and Transversal Lines
When a line intersects any two parallel lines, we call it a transversal. In this arrangement, many pairs of angles are formed. Among these, some angles are congruent (equal) while others are supplementary.
Now, let us observe the following figure to see the parallel lines labelled as l1 and l2 that intersect by a transversal:
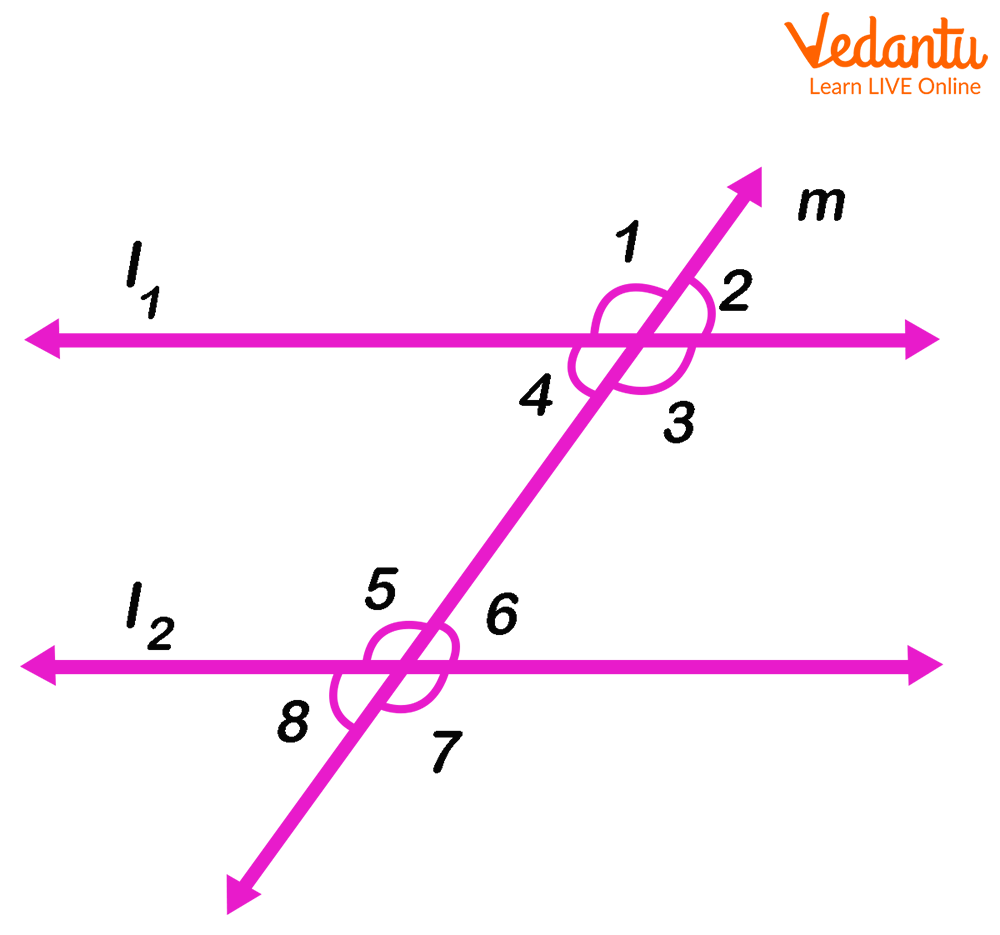
Parallel Lines
In this figure, eight separate angles have been formed by the two parallel lines and a transversal. Each angle has been labelled using numbers.
Corresponding Angles:
In the given figure, there are four pairs of corresponding angles, that is, ∠1 = ∠5, ∠2 = ∠6, ∠4 = ∠8, and ∠3 = ∠7.
Alternate Interior Angles:
Angles that formed on the inside of two parallel lines that are intersected by a transversal are alternate interior angles. They are equal in measure. In this figure, ∠4 = ∠6 and ∠3 = ∠5.
Alternate Exterior Angles:
Alternate exterior angles are formed on either side of the transversal and they are equal in measure. In this figure, ∠1 = ∠7 and ∠2 = ∠8.
Consecutive Interior Angles:
Consecutive interior angles or co-interior angles are formed on the inside of the transversal and they are supplementary. Here, ∠3 + ∠6 = 180° and ∠4 + ∠5 = 180°.
Vertically Opposite Angles:
Angles formed when two straight lines intersect each other and they are equal in measure, we call them vertically opposite angles. Here, ∠1 = ∠3, ∠2 = ∠4, ∠5 = ∠7, and ∠6= ∠8.
Parallel lines Equation
The equation of a straight line is written in the slope-intercept form represented by the following equation:
y = mx + b
Here, 'm' is the slope and 'b' is the y-intercept.
Please note that the value of 'm' determines the slope or gradient and tells us how steep the line is. Also, it should be noted that the slope of any two parallel lines is always the same.
Assume that the slope of a line with the equation y = 4x + 3 is 4. Thus, any line that is parallel to y = 4x + 3 will also have the same slope, that is, 4.
We must remember that parallel lines have different y-intercepts and have no points in common.
Which Lines Appear to be Parallel?
Apart from the characteristics of parallel lines given above, when any two parallel lines are intersected by a transversal, we can understand the lines that appear to be parallel by the following properties:
Two lines are parallel when the corresponding angles so formed are equal.
Two lines are parallel when the alternate interior angles so formed are equal.
Two lines are parallel when the alternate exterior angles so formed are equal.
Two lines are parallel when the consecutive interior angles on the same side of the transversal are supplementary.
From the above text, we understand that parallel lines are equidistant and meet at infinity. Also, all the lines parallel to them will have the same slope, i.e., m.
FAQs on Parallel Lines in Geometry Explained Clearly
1. What are parallel lines in geometry?
Parallel lines are two lines in the same plane that never intersect and remain the same distance apart at all points. In geometry, parallel lines have:
- No point of intersection
- A constant distance between them
- The same direction or slope (in coordinate geometry)
2. How do you know if two lines are parallel?
Two lines are parallel if they have the same slope (in coordinate geometry) or if certain angle pairs formed by a transversal are equal. You can check parallel lines by:
- Comparing slopes: if m₁ = m₂, the lines are parallel.
- Checking angles: corresponding angles or alternate interior angles are equal.
- Verifying that co-interior angles add up to 180°.
3. What is the symbol for parallel lines?
The symbol for parallel lines is ||. For example, if line AB is parallel to line CD, we write AB || CD. This notation is commonly used in geometry problems, proofs, and diagrams to show that two lines do not intersect and remain equidistant.
4. What is the slope of parallel lines?
The slope of parallel lines is equal. In coordinate geometry, if one line has slope m, any line parallel to it will also have slope m. For example:
- Line 1: y = 2x + 3 → slope = 2
- Line 2: y = 2x − 5 → slope = 2
5. What angles are equal when parallel lines are cut by a transversal?
When parallel lines are cut by a transversal, corresponding angles and alternate interior angles are equal. The important angle relationships are:
- Corresponding angles are equal.
- Alternate interior angles are equal.
- Co-interior (consecutive interior) angles add up to 180°.
6. How do you write the equation of a line parallel to another line?
To write the equation of a line parallel to another line, use the same slope and a different intercept. Steps:
- Identify the slope m of the given line.
- Use the point-slope formula: y − y₁ = m(x − x₁).
- Simplify to slope-intercept form if needed.
- Slope m = 3
- y − 4 = 3(x − 2)
- y = 3x − 2
7. What is the difference between parallel and perpendicular lines?
Parallel lines never meet, while perpendicular lines intersect at a 90° angle. The key differences are:
- Parallel lines: Same slope, never intersect.
- Perpendicular lines: Slopes are negative reciprocals (m₁ × m₂ = −1).
8. Can parallel lines ever intersect?
No, parallel lines never intersect in Euclidean geometry. By definition, parallel lines lie in the same plane and remain equidistant forever. If two lines intersect at any point, they are not parallel.
9. What is a real-life example of parallel lines?
A real-life example of parallel lines is railway tracks, which remain the same distance apart and never meet. Other examples include:
- Opposite edges of a rectangle
- Lines on ruled paper
- Road lane markings
10. How do you solve problems involving parallel lines and angles?
To solve problems involving parallel lines and angles, use the angle relationships formed by a transversal. Follow these steps:
- Identify equal angles (corresponding or alternate interior).
- Use the fact that co-interior angles sum to 180°.
- Set up an equation and solve for the unknown.
