How to Add Hexadecimal Numbers Step by Step with Examples
The letters "Hexa" and "deci" in the phrase "hexadecimal" stand for the numbers "6" and "10," respectively. The 16-digit hexadecimal representation of numerals 0 through 9 and letters A through F is known as the hexadecimal number system. To put it another way, the first nine numbers or digits are represented as numbers, while the next six digits are represented by the letters A through F. The decimal number system, which has a base of 9, and hexadecimal are quite similar. Therefore, after 9 digits, the 10th digit is represented as a symbol - 10 as A, 11 as B, 12 as C, 13 as D, 14 as E and 15 as F.
What are Hexadecimal Numbers?
Since each digit has a weight of power 16, the hexadecimal number system is also known as a positional number system. Each subsequent digit is 16 times more important than the one before it. For example : \[7B{3_{16}}\] ,\[4B2{A_{16}},67{F_{16}}{\rm{ \;and }}{76_{16}}\]
Hexadecimal Addition of Numbers
The only difference between hex addition and decimal addition is the addition of the letters A, B, C, D, E and F. Here is an illustration of hex addition. Check the example provided below, and for further information, see the paragraph below it.
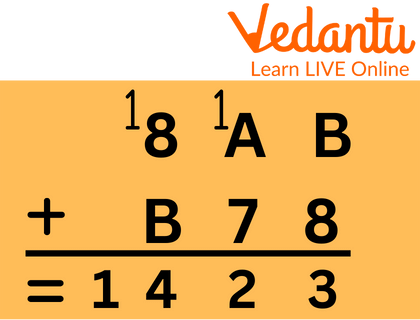
Example for Hexadecimal Addition
When numbers higher than 9 (the letters A through F) are present, hex addition includes calculating basic decimal addition while converting between hex and decimal. In the example, B + 8 equals 11 + 8 or 19.
Hexadecimal Table
You can perform hexadecimal addition much easier if you use the table below.
Hexadecimal Table
How to Add Hexadecimal Numbers
The decimal number system, which has a base of 9, and the hexadecimal are quite similar. We can very easily add hexadecimal numbers by understanding the hexadecimal table and following simple addition.
Let’s understand it with the help of a example:
Addition of Hexadecimal Numbers
Here, we will add from ones place:
So, 3 + 1 = 4
Now, add tens place with the help of the hexadecimal table
b + 2 = d
Add the hundredth place now.
f + 6 = 15 (1will be in carry)
7 + b = 12
And as 1 was in carry over, so 12 + 1 = 13
Now, at last 1 + 1 = 2
Thus, the final answer is 235d4.
Solved Examples
Example 1: Add the following hexadecimal number.
8AB + B78
Ans: 8AB + B78
We know:
8 + B = 13
A + 7 = 11
8 + B = 13
8AB + B78 = 1423
Thus, the answer is 1423.
Example 2: Add the following hexadecimal numbers.
D6E + 8C6
Ans: We know that
E + 6 = 14
6 + C = 12
D + 8 = 15
Thus,
D6E + 8C6
= 1634
Therefore, its sum will be 1634.
Example 3: What use does the hexadecimal number system serve?
Ans: Hexadecimal number system applications:
There is a way to write numbers in hexadecimal. Symbols are used when we write numbers. We continue adding digits and adding colour references until there are no more symbols left. Assembly language programming errors can also occur.
Conclusion
The hexadecimal number system is also referred to as a positional number system since each digit has a power 16 value. The importance of each digit after the first one increases by a factor of 16.
FAQs on Addition of Hexadecimal Numbers Explained Clearly
1. What is addition of hexadecimal numbers?
The addition of hexadecimal numbers is the process of adding numbers written in base 16 using digits 0–9 and A–F. In the hexadecimal number system:
- Digits go from 0 to 9 and A (10) to F (15).
- Addition is performed column by column, similar to decimal addition.
- If a sum is 16 or more, you carry over to the next column.
2. How do you add two hexadecimal numbers step by step?
To add two hexadecimal numbers, add each column from right to left and carry when the sum is 16 or more. Follow these steps:
- Step 1: Align the numbers by place value.
- Step 2: Add the rightmost digits.
- Step 3: If the sum ≥ 16, write the remainder and carry 1.
- Step 4: Repeat for remaining columns.
Add 2A + 1F
- A (10) + F (15) = 25 → 25 ÷ 16 = 1 remainder 9
- Write 9, carry 1
- 2 + 1 + 1 (carry) = 4
3. What are the rules for carrying in hexadecimal addition?
In hexadecimal addition, you carry over when the sum of digits is 16 or more. The rules are:
- If sum < 16 → write the sum directly.
- If sum ≥ 16 → subtract 16 and carry 1 to the next column.
- Remember A=10, B=11, C=12, D=13, E=14, F=15.
4. Can you give an example of hexadecimal addition with carry?
Yes, hexadecimal addition with carry works like decimal addition but in base 16. Example: Add 7D + 8E.
- D (13) + E (14) = 27 → 27 − 16 = 11 (B), carry 1
- 7 + 8 + 1 (carry) = 16 → write 0, carry 1
- Final carry = 1
5. Why is hexadecimal addition used in computer science?
Hexadecimal addition is used in computer science because hexadecimal numbers provide a compact representation of binary values. Key reasons include:
- Each hex digit represents 4 binary bits.
- It simplifies reading large binary numbers.
- Commonly used in memory addresses and machine code.
6. How do you add hexadecimal numbers by converting to decimal?
You can add hexadecimal numbers by converting them to decimal, adding them, and converting back to hexadecimal. Steps:
- Step 1: Convert each hex number to decimal.
- Step 2: Add the decimal values.
- Step 3: Convert the result back to hexadecimal.
- A = 10 (decimal)
- 10 + 5 = 15
- 15 in hex = F
7. What is the formula for hexadecimal place value?
The place value of a hexadecimal number is based on powers of 16. The formula is:
Digit × 16ⁿ, where n is the position from right to left starting at 0.
- Rightmost digit → 16⁰
- Next digit → 16¹
- Next digit → 16²
8. What is the difference between binary and hexadecimal addition?
The main difference is that binary addition is base 2, while hexadecimal addition is base 16. Key differences:
- Binary digits: 0 and 1
- Hex digits: 0–9 and A–F
- Binary carries at 2; hexadecimal carries at 16.
9. What are common mistakes in hexadecimal addition?
Common mistakes in hexadecimal addition include incorrect digit values and forgetting to carry at 16. Typical errors:
- Confusing A–F values (A=10, F=15).
- Not carrying when sum ≥ 16.
- Incorrect conversion between hex and decimal.
10. How do you check your hexadecimal addition answer?
You can check hexadecimal addition by converting the numbers to decimal and verifying the sum. Steps:
- Convert both hex numbers to decimal.
- Add them in decimal form.
- Convert your hexadecimal result to decimal.
- Compare both decimal sums.
