




How to Identify and Use Intersecting Lines in Math Problems
Understanding Intersecting Lines and Their Use
Before going deep into the concept of intersecting lines, let us understand the meaning of a line in Geometry. So, what is a line? In simple language, a line can be defined as something that consists of indefinite points which are extending in different directions. For example, let us take two points A and B. Now, a line can be drawn joining the two points A and B. This line extends in both directions and is called line AB. A line has no ends and is illustrated using arrows to indicate that it extends indefinitely.

A Line Passing through Points A and B
Now, let us consider two or more lines and imagine that they are all passing through a common point. In such conditions, the point they share is called the intersecting point and all the lines are called intersecting lines. Therefore, we can define intersecting lines as two or more lines that cross each other and share a common point in a plane.

Intersecting Line and Point of Intersection
In the above picture, line A and line B share a common point of intersection, i.e., x. Hence, both line A and line B are called intersecting lines.
But can all lines that intersect each other be called intersecting lines? No. We must keep in mind the following points to understand the properties of intersecting lines.
What are the Properties of Intersecting Lines?
Knowing the properties of intersecting lines is very important as not all lines can be called intersecting lines. One must know the difference between intersecting and non-intersecting lines. Given below are a few of the properties of intersecting lines:
The intersecting lines can meet at only one common point.
The intersecting lines can meet at any angle, i.e, from 0° to 180°.
No two straight lines can meet at more than one point.
If two lines are meeting at more than one point, then they are not intersecting lines as no two straight lines can intersect each other at more than one point.
When two lines intersect each other, they form a pair of vertical angles. These angles share a common vertex or the point of intersection and are faced opposite to each other.
The vertical angles are always equal to each other.
Given below are two images, image 1 and image 2, showing intersecting lines. In image 1, several lines intersect each other, passing through only one common point. Hence, all these lines are intersecting lines.
In image 2, there are three pairs of intersecting lines. In each pair, both lines are intersecting each other through one common point. Hence, all three pairs are intersecting lines too.

Intersecting Lines

Intersecting Lines
Examples of Intersecting Lines
We can find some examples of intersecting lines in our day to day life too. For example, we all use scissors to cut paper but have you noticed that the two sharp blades of the scissors are connected to each other at a common point. Hence, they are intersecting each other and are an example of intersecting lines.

A Scissor
Similarly, we can find two roads that are meeting each other and intersecting each other at one common point.

Intersecting Roads
Now, let us do a fun activity. We have provided you with a picture. You will have to look at the picture below and identify the intersecting and non-intersecting lines from them.

A Picture Showing Intersecting and Non-Intersecting Lines
From the above picture, we can identify that line KL, line PQ, line CD, and line MN share a common intersecting point, i.e, O. Hence, they are the intersecting lines.
Whereas, line AB, line CD, and line EF are parallel lines and do not intersect each other. Hence, they are the non-intersecting lines.
Great! You have now understood how to identify intersecting lines and what are their main properties. We hope you had fun learning about this topic and doing this fun activity. To find more information and questions on intersecting lines and geometry, you can visit our website.
Properties of Lines without Intersections
If we take into account that lines without intersections have the following characteristics, we can identify them:
Lines without intersections never cross each other and have no point of intersection.
These lines are equidistant, that is, they always maintain the same distance from each other.
Lines without intersections have the same slope.
Solved Examples
Example 1: Are the following lines intersecting lines or lines without intersections?
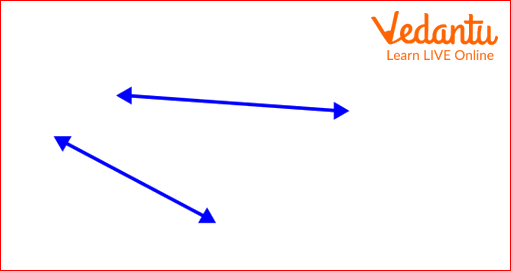
Intersecting lines or not
Solution: Lines have directions, which means they extend indefinitely to both sides. If we extend them enough, we can see that they would cross, since they have different inclinations. Therefore, the lines are intersecting.
Example 2: What are some real-world examples of intersecting lines?
Solution: Here are some instances of intersecting lines:
Crossroads: A straight-line intersection is created when two straight roadways cross.
Scissors: Scissors have two sides that meet at a line intersection.
Railroad Rails: The rails cross and form intersecting lines when there are multiple railroad tracks.
Example 3: What is true and what is untrue about the statements that follow?
1. Pair of vertical angles are formed by two intersecting lines.
2. A point of intersection can be shared by three intersecting lines.
3. Four pairs of vertical angles are created by two intersecting lines.
4. Four common points of intersection cannot be shared by three intersecting lines.
Solution: We have the following:
1. Four angles are created by two intersecting lines. Angles that are directly opposite one another are all vertical. So, this is accurate.
2. A single point of intersection can be shared by three intersecting lines. So, this is accurate.
3. Only two pairs of vertical angles are formed when two intersecting lines generate two angles. This is untrue.
4. A maximum of three crossing locations can be shared by three intersecting lines. So, this is untrue.
Key Features of Intersecting Lines
They are straight lines that intersect at a common point.
Intersecting lines are not equidistant from each other.
Intersecting lines cut each other at the point of intersection.
When intersecting lines intersect, they form four angles; two internal and two external, which are characterised by being equal to each other.
Practice Questions
1. Find the point of intersection of lines 4x+8y+4=0 and 2x+3y+5=0 using the point of intersection formula.
Ans: (-7,3)
2. What will be the point of intersection of lines 2x+4y+6=0 and 12x+18y+24=0?
Ans: (1,-2)
FAQs on Intersecting Lines: Meaning, Properties, and Everyday Examples
1. Can perpendicular lines be also called intersecting lines?
Yes, perpendicular lines are a special type of intersecting lines. They intersect each other at one point forming a 90° angle.
2. What are non-intersecting lines?
Non-intersecting lines are also known as parallel lines. These lines can be defined as two lines that never intersect or meet each other at a common point. The distance between two non-intersecting lines is always the same.
3. What is the maximum number of intersections of 4 non-parallel lines?
The maximum number of interaction points of n non-parallel lines is \[\dfrac {n\times (n-1)}{2}\].
The maximum number of intersection points of 4 non-parallel lines is
\[\dfrac{4(4-1)}{2}\] = 6
4. What is the x-intercept of a line?
The intersection point of the x-axis and a line is known as the x-intercept of a line.
5. What is the coordinate of the intersection point of two axes?
Two axes in the coordinate plane are the x-axis and the y-axis. The x-axis and y-axis intersect at the origin. The coordinate of the intersection point of the two axes is (0,0).























