




Angle Names, Properties, and How to Identify Each Type
In geometry, an angle is formed when two rays or lines meet at a common point, and each angle has its own unique measure. Angles play a crucial role in the study of geometry, forming the foundation for more complex shapes and figures. There are various types of angles based on their measurements, including acute angles, obtuse angles, right angles, reflex angles, and straight angles. For instance, an acute angle is one that is less than 90°, while an obtuse angle is greater than 90°. Additionally, there are special types of angle pairs that are essential in geometric constructions. This page will guide you through the different types of angles, their characteristics, and how they are used in geometry.
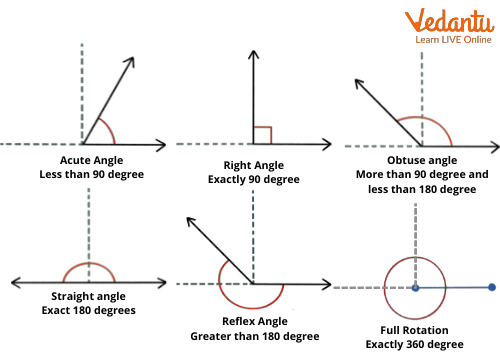
Parts of an Angle
1. Vertex: The vertex is the point where the two arms of the angle meet. It is the common endpoint of the rays that form the angle.
2. Arms: The arms are the two straight line segments that extend from the vertex. These lines form the angle.
3. Angle: The angle is the measure of the rotation of a ray about its endpoint, or the space between its initial and final position. The angle is typically measured in degrees (°) or radians.
Types of Angles Based on Rotation
The next classification of angles is based on the direction of rotation of one arm of the angle. When two lines intersect and meet at a common point, an angle is formed. The measurement and nature of the angle can vary depending on the direction in which one arm rotates. In this section, we will discuss the types of angles based on rotation, which include various angle categories such as acute, obtuse, and reflex, each determined by the extent of the rotation between the arms.
Different Types of Angles
There are various types of angles based on their measure of the angle. The types are:
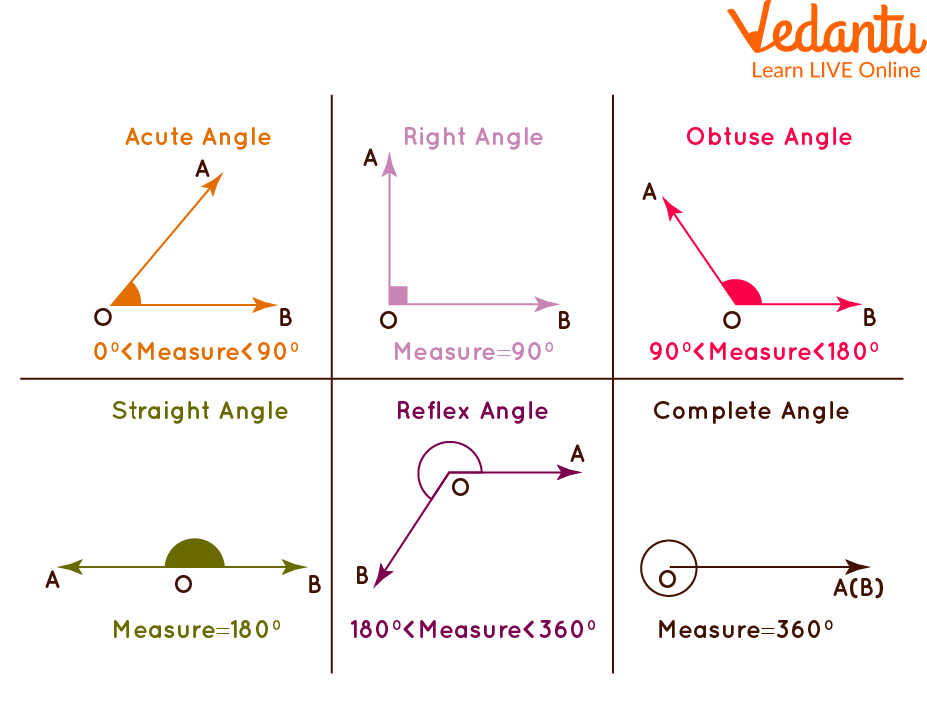
1. Acute angle
2. Right angle
3. Obtuse angle
4. Straight angle
5. Reflex angle 4. Complementary & Supplementary Angles
How to measure Different Types of Angles?
1. Acute Angle
An angle which measures less than 90° is called an acute angle. The measure between 0° to 90°. In the picture below, the angle formed by the intersection of PQ and QR at Q forms an angle PQR which measures 45°. Thus, PQR is called an acute angle.
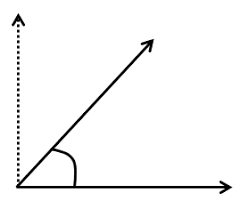
2. Right Angle
An angle which measures exactly 90° is called a right angle. It is generally formed when two lines are perpendicular to each other. In the figure below, line AB intersects line BC at B and forms an angle ABC which measures 90°.
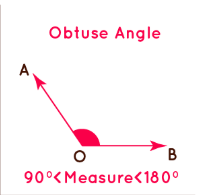
3. Obtuse Angle
An angle that measures greater than 90° is known as the obtuse angle. The angle measure ranges from 90° to 180°. An obtuse angle can also be found out if we have the measure of the acute angle.
Obtuse Angle Measure = (180 - acute angle measure)
In the picture above, line segment DO intersects line segment OQ at point O and forms an angle DOQ measuring 120°. Thus, it is an obtuse angle.
Also, if we extend line OQ to OP then we can find a measure of the acute angle.
DOP = 180° - DOQ = 180° - 120° = 60°
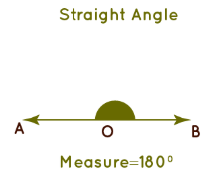
4. Straight Angle
The angle which measures exactly 180° is called a straight angle. This is similar to a straight line, thus the name straight angle.
A straight angle is nothing but a mixture of an obtuse angle and acute angle on a line.
5. Reflex Angle
The angle which measures greater than 180° and less than 360° is known as the reflex angle. The reflex angle can be calculated if the measure of the acute angle is given, as it is complementary to the acute angle on the other side of the line.
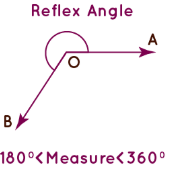
Using the reflex angle, we can find the measure of the acute angle.
A Measure of Acute Angle = 360° – a Measure of Reflex Angle
6. Complementary & Supplementary Angles
Complementary Angle
If two angles add up to measure 90° then they are known as complementary angles. The angles don't have to be adjacent to each other to be known as complementary. As long as they add up to 90° they will be known as complementary angles.
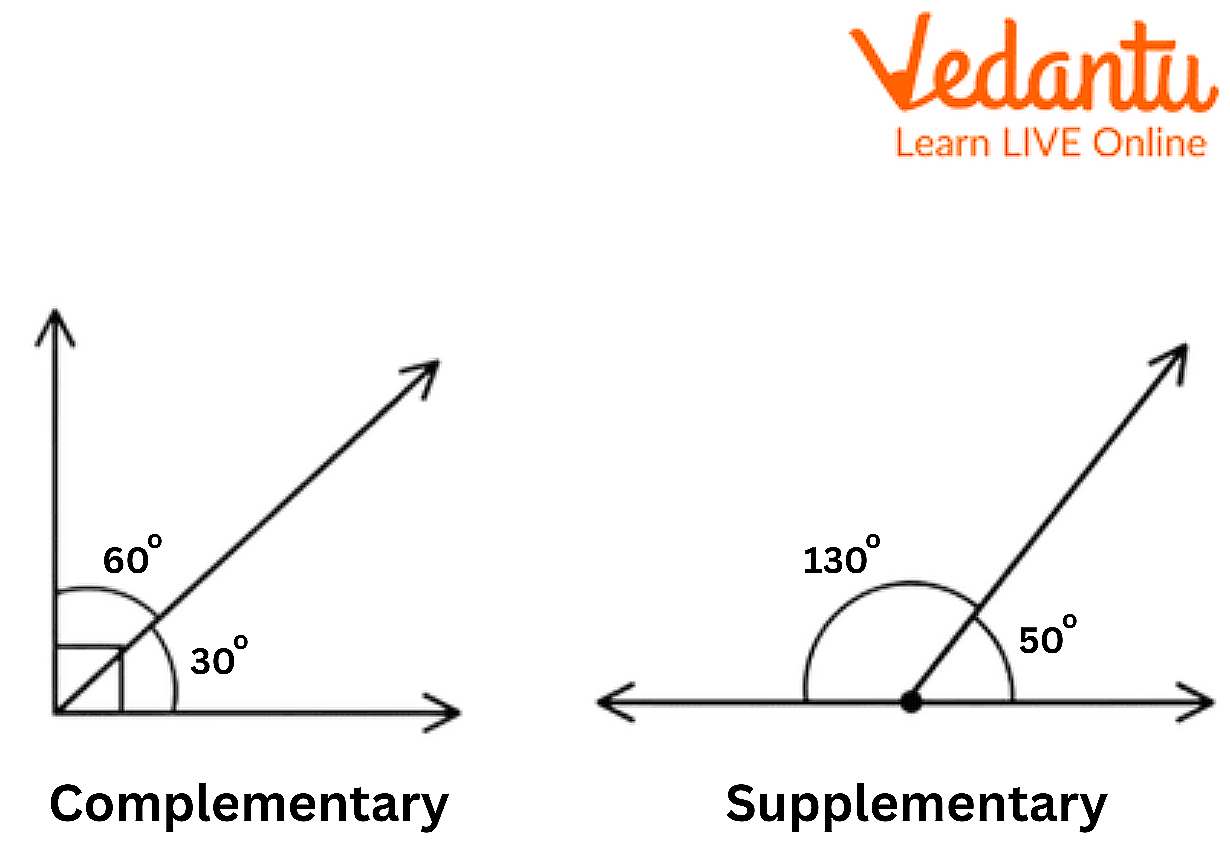
In the above figure, the angles are present adjacent to each other and add up to 90° and thus are known as complementary angles. In figure c and d, the angles are not adjacent to each other, but they add up to 90° and thus they are known as complementary angles.
Supplementary Angles
When two angles add up to 180° then they are known as supplementary angles. There are various types of supplementary angles.
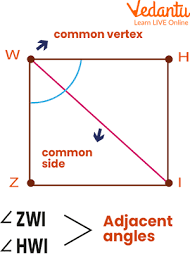
Adjacent angles
These angles have a common side and vertex, i.e., a corner point. However, these points do not overlap in any way. In simpler terms, adjacent angles are two angles next to each other.
Non-adjacent angles
These angles do not have a common endpoint, i.e They usually do not have a common vertex.
Types of Non-adjacent angles-
Vertical Angles
Angles which have a common vertex and the sides of the angle are formed by the same lines are known as vertical angles. Vertical angles are equal to each other.
(Image will be Uploaded Soon)
In the above figure, 1 and 3, 2 and 4, 6 and 8 and 5 and 7 are vertical angles. Also, 3, 4,5, 6 are known as interior angles and 1,2,7,8 are known as exterior angles.
Alternate Interior Angles
These are a pair of interior angles present on the opposite side of the transversal. The easiest way to spot alternate interior angles is to identify a "Z” on the interior side.
In the above figure, 3 and 5, 4 and 6 are interior angles. The interior angles are equal to one another.
Alternate Exterior Angles
This is similar to alternate interior angles; just that it is present on the exterior side. In the above figure, 1 and 7, 2 and 8 are the pair of alternate exterior angles. Similar to alternate interior angles, even alternate exterior angles are equal to one another.
Corresponding Angles
Angles which are present in a similar position are known as corresponding angles. In the above figure, 1 and 5 are corresponding angles and they are equal to one another.
Types of Angles Based on Rotation
The next classification of angles is based on the direction of rotation of one arm of the angle. When two lines intersect and meet at a common point, an angle is formed. The measurement and nature of the angle can vary depending on the direction in which one arm rotates. In this section, we will discuss the types of angles based on rotation, which include various angle categories such as acute, obtuse, and reflex, each determined by the extent of the rotation between the arms.
Based on the direction of rotation, you can classify angles
Positive Angles
Negative Angles
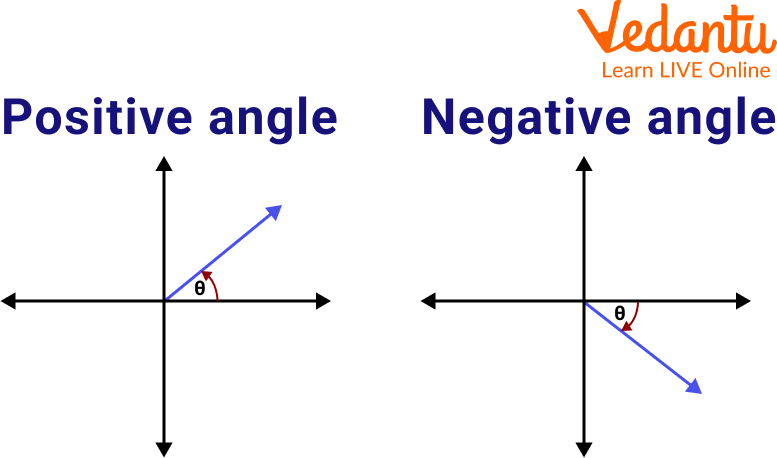
Positive angles: The angles are measured in the counterclockwise direction (opposite to the direction in which the clock turns) starting from the angle base.
Negative angles: These angles are measured in the clockwise direction starting from the angle base.
Summary
The major basis of geometry is angles. Angles finds its application in nearly all types of questions, be it trigonometry to closed shapes. Understanding angles and angle types will help in solving a lot of tricky questions. Thus, make sure that you understand it well.























