Question

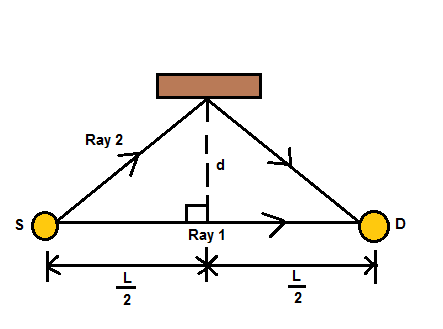
In figure the sound of wavelength $0.850m$ is emitted isotropically by point source S. Sound ray 1 extends directly to detector $D$, at distance $L=10.0m$. Sound ray 2 extends to D via a reflection (effectively, a “bouncing”) of the sound at a flat surface. That reflection occurs on a perpendicular bisector to the $SD$ line, at distance $d$ from the line. Assume that the reflection shifts the sound wave by $0.500\lambda $. For what value of $d$ (other than zero) do the direct sound and the reflected sound arrive at $D$ exactly out of phase?

Answer 1

Hint: Firstly, we must know how to write the equation for the path difference. Then we can set the equation for the path difference equal to the condition for the destructive interference, and finally, get the value for the required variable $d$.

Formula used
$\Delta x=(2n+1)\dfrac{\lambda }{2}$

Complete step by step solution:
Generally, the equation for path difference is given by:
$\Delta x=$ distance travelled by ray 2 – distance travelled by ray 1, assuming $\Delta x$ is path difference.
From the diagram, we can find the distance travelled by ray 1 and ray 2.
Distance travelled by ray 1:
${{L}_{1}}=\dfrac{L}{2}+\dfrac{L}{2}=L$
According to the question, $L=10m$.
Therefore, distance travelled by ray 1 is $10m$ .
Distance travelled by ray 2:
In the left triangle and right triangle, formed by the perpendicular bisector of SD line. Applying Pythagoras theorem in these triangles, we get:
Assuming hypotenuse to be $x$, \[{{x}^{2}}={{\left( \dfrac{L}{2} \right)}^{2}}+{{d}^{2}}\]
Hence, $x=\sqrt{{{\left( \dfrac{L}{2} \right)}^{2}}+{{d}^{2}}}$
For a right triangle, the hypotenuse is the same as the left triangle.
According to the question, reflection adds $\dfrac{\lambda }{2}$ factor to the path length.
Therefore, distance travelled by ray 2 is:
${L_2} = x + \dfrac{\lambda }{2} + x = 2x + \dfrac{\lambda }{2} $
 $ {L_2} = 2\sqrt {{{\left( {\dfrac{L}{2}} \right)}^2} + {d^2}} + \dfrac{\lambda }{2} $
Path difference is given by:
 $ \Delta x = {L_2} - {L_1}$
 $ \Rightarrow \Delta x = 2\sqrt {{{\left( {\dfrac{L}{2}} \right)}^2} + {d^2}} + \dfrac{\lambda }{2} - L $
For destructive interference, $\Delta x=(2n+1)\dfrac{\lambda }{2}$
$\Rightarrow \sqrt{{{L}^{2}}+{{(2d)}^{2}}}-L+\dfrac{\lambda }{2}=(2n+1)\dfrac{\lambda }{2}$
$\Rightarrow \sqrt{{{L}^{2}}+{{(2d)}^{2}}}-L=n\lambda $
Substituting the values, $L=10m$, $\lambda=0.850m$, and let $n=1$,
$ \sqrt {{{10}^2} + {{(2d)}^2}} - 10 = 1 \times 0.850$
 $\Rightarrow \sqrt {{{10}^2} + {{(2d)}^2}} = 10.850$
Squaring both sides,
  $ \Rightarrow 100 + 4{d^2} = 117.7225$
   $\Rightarrow {d^2} = \dfrac{{17.7225}}{4}$
  $ \Rightarrow d = \sqrt {4.430} $
Solving this equation for $d$, we get:
$d=0,2.10m,...$
As given in the question, $d\ne 0$

Therefore, $d=2.10m$.

Note: We must know the condition for the resultant wave when the interference of two waves is being observed, i.e. the conditions for the constructive interference and the destructive interference. If we already know the formula for the interference condition, we only have to find out the path difference and sometimes phase difference also.
Formula for phase difference is: $\Delta \theta =2\pi \dfrac{\Delta x}{\lambda }$, where $\Delta \theta $ is phase difference.