Important Questions for CBSE Class 11 Physics Chapter 1 - Units and Measurement

Very Short Questions and Answers (1 Marks Questions)

1. What is the difference between $\overset{{}^\circ }{\mathop{A}}\,$ and A.U.?

Ans:  Angstrom (\[\overset{{}^\circ }{\mathop{A}}\,\]) and astronomical unit (A.U.) are both the units of distance. 

However, their values are very different. Their values in SI unit of distance are: $1{{A}^{0}}={{10}^{-10}}m$ and $1A.U.=1.496\times {{10}^{11}}m$. 

2. Define S.I. Unit of Solid Angle.            

Ans: The SI unit of solid angle is steradian. One steradian is defined as the angle made by a spherical plane of unit square meter area at the centre of a sphere with radius of unit length.

3. Name Physical Quantities Whose Units are Electron Volt and Pascal.           

Ans: The physical quantities whose units are electron volt and pascal are energy and pressure respectively.

4. Fill ups.

1. $3.0m/{{s}^{2}}=$ ………….$km/h{{r}^{2}}$

Ans: 

$3.0m/{{s}^{2}}=$ ………….$km/h{{r}^{2}}$

We have, $1m={{10}^{-3}}km$

$1hr=3600s$

$\Rightarrow 1{{s}^{2}}={{\left( \frac{1}{3600} \right)}^{2}}h{{r}^{2}}$

Then, 

 $3.0m/{{s}^{2}}=\frac{3\times {{10}^{-3}}}{{{\left( \frac{1}{3600}h \right)}^{2}}}km/h{{r}^{2}}$

$\therefore 3.0m/{{s}^{2}}=3.9\times {{10}^{4}}km/h{{r}^{2}}$ 

2. \[6.67\times {{10}^{-11}}N{{m}^{2}}/k{{g}^{2}}=\] ……….. \[{{g}^{-1}}c{{m}^{3}}{{s}^{-2}}\]

Ans:

We have,

$1N=1kgm{{s}^{-2}}$

$1kg={{10}^{-3}}g$

$1{{m}^{3}}={{10}^{6}}c{{m}^{3}}$

\[\Rightarrow 6.67\times {{10}^{-11}}N{{m}^{2}}k{{g}^{-2}}=6.67\times {{10}^{-11}}\times \left( 1kgm{{s}^{-2}} \right)\left( 1{{m}^{2}} \right)\left( 1{{s}^{-2}} \right)\]

\[=6.67\times {{10}^{-11}}\times \left( 1kg\times 1{{m}^{3}}\times 1{{s}^{-2}} \right)\]

\[=6.67\times {{10}^{-11}}\times \left( {{10}^{-3}}{{g}^{-1}} \right)\left( {{10}^{6}}c{{m}^{3}} \right)\left( 1{{s}^{-2}} \right)\]

$\therefore 6.67\times {{10}^{-11}}N{{m}^{2}}/k{{g}^{2}}=6.67\times {{10}^{-8}}c{{m}^{3}}{{s}^{-2}}{{g}^{-1}}$

Very Short Questions and Answers (2 Marks Questions)

1. When a planet X is at a distance of 824.7 million kilometres from earth its angular diameter is measured to be $35.72''$ of arc. Calculate the diameter of planet X.         

Ans: 

Distance between planet X and earth, $r=824.7\times {{10}^{6}}km$. 

The angular diameter $\theta $ is given to be,

$\theta =35.72''$

$\theta =\frac{35.72}{60\times 60}\times \frac{\pi }{180}radian$

Diameter $l=?$ 

We have the relation,

$l=r\theta $ 

$\Rightarrow l=824.7\times {{10}^{6}}\left( \frac{35.72}{60\times 60}\times \frac{\pi }{180} \right)$

$\therefore l=1.429\times {{10}^{5}}km$

2. A Radar Signal Is Beamed Towards a Planet from the Earth and Its Echo is Received Seven Minutes Later. Calculate the Velocity of the Signal, If the Distance Between the Planet and the Earth is \[6.3\times {{10}^{10}}m\].

Ans: 

Time after which the echo is received, $t=7\min =7\times 60s$.

Distance between the planet and earth, $x=6.3\times {{10}^{10}}m$.

The net distance covered while the radar signal reaches the planet and echo to reach back to earth $2x$.

We know that the velocity is defined as the net distance covered per total time taken. So, 

$c=\frac{2x}{t}$ 

$\Rightarrow c=\frac{2\times 6.3\times {{10}^{10}}}{7\times 60}$

$\therefore c=3\times {{10}^{8}}m/s$

3. Find the Dimensions of Latent Heat and Specific Heat.

Ans: 

It is known that:

Latent Heat $=\frac{Q\left( \text{Heat energy} \right)}{m\left( \text{mass} \right)}$ 

Dimension of Latent Heat $=\frac{M{{L}^{2}}{{T}^{-2}}}{M}=[{{M}^{0}}{{L}^{2}}{{T}^{-2}}]$ 

Specific Heat:

$S=\frac{Q}{m\Delta T}$

$\Rightarrow \left[ S \right]=\frac{\left[ Q \right]}{\left[ m\Delta T \right]}=\frac{M{{L}^{2}}{{T}^{-2}}}{M\times K}$

$\therefore \left[ S \right]=[{{M}^{0}}{{L}^{2}}{{T}^{-2}}{{K}^{-1}}]$

4. What are the dimensions of ‘a’ and ‘b’ in Vander Waals equation $\left( P+\frac{a}{{{V}^{2}}} \right)\left( V-b \right)=RT$ ?                                                                                                                             

Ans: We know that physical quantities undergoing addition or subtraction should be of the same dimension. 

So, $\frac{a}{{{V}^{2}}}$will have the same dimensions as $P$ and $b$ will have the same dimensions as $V$. 

So,

$\left[ P \right]=\left[ \frac{a}{{{V}^{2}}} \right]\Rightarrow \left[ a \right]=\left[ P{{V}^{2}} \right]$ 

$\Rightarrow \left[ a \right]=\left[ \frac{F}{A}\times {{V}^{2}} \right]$ 

$\Rightarrow \left[ a \right]=\frac{\left[ ML{{T}^{-2}} \right]}{\left[ {{L}^{2}} \right]}\times {{\left[ {{L}^{3}} \right]}^{2}}$

$\Rightarrow \left[ a \right]=\frac{ML{{T}^{-2}}{{L}^{6}}}{{{L}^{2}}}$

Therefore, the dimension of ‘a’ would be, 

$\therefore \left[ a \right]=\left[ M{{L}^{5}}{{T}^{-2}} \right]$

Also, $\left[ b \right]=\left[ V \right]$ 

Therefore, the dimension ‘b’ would be,

$\therefore \left[ b \right]=\left[ {{M}^{0}}{{L}^{3}}{{T}^{0}} \right]$

5. If $E,m,l$ and $G$ denote energy, mass, angular momentum and gravitational constant respectively, determine the dimensions of $\frac{E{{L}^{2}}}{{{m}^{5}}{{G}^{2}}}$ .

Ans: 

We have, dimensions of:

$E=\left[ M{{L}^{2}}{{T}^{-2}} \right]$ 

$L=\left[ M{{L}^{2}}{{T}^{-1}} \right]$ 

$m=\left[ M \right]$ 

$G=\left[ {{M}^{-1}}{{L}^{3}}{{T}^{-2}} \right]$ 

Now, the dimensions of $\frac{E{{L}^{2}}}{{{m}^{5}}{{G}^{2}}}$could be written as,

$=\frac{\left[ M{{L}^{2}}{{T}^{-2}} \right]{{\left[ M{{L}^{2}}{{T}^{-1}} \right]}^{2}}}{{{\left[ M \right]}^{5}}{{\left[ {{M}^{-1}}{{L}^{3}}{{T}^{-2}} \right]}^{2}}}$

$=\frac{{{M}^{3}}{{L}^{6}}{{T}^{-4}}}{{{M}^{3}}{{L}^{6}}{{T}^{-4}}}=1$

Therefore, the given term is dimensionless. 

6. Calculate the time taken by light to pass through a nucleus of diameter $1.56\times {{10}^{-16}}m$. (Take the speed of light to be $c=3\times {{10}^{8}}m/s$).

Ans: 

We know that speed could be defined as the total distance covered per unit time. Mathematically,

$c=\frac{x}{t}$

$\Rightarrow t=\frac{x}{c}$

Here, the net distance covered is the diameter of the nucleus. Now, on substituting the given values, we get, 

$t=\frac{1.56\times {{10}^{-16}}}{3\times {{10}^{8}}}$

$\therefore t=5.2\times {{10}^{-25}}s$

Therefore, we found that light takes $t=5.2\times {{10}^{-25}}s$ to cross the given nucleus. 

7. Express the dimension of energy if F, A and T are considered as the base quantities. (Where, F stands for force, A for acceleration and T for time). 

Ans: 

We know that, dimension of acceleration, $\left[ A \right]=\left[ L{{T}^{-2}} \right]$…….. (1)

By Newton's second law of motion, 

$F=MA$

$\Rightarrow M=F{{A}^{-1}}$……. (2)

Now, we know that the dimension of energy is generally given by, $\left[ E \right]=\left[ M{{L}^{2}}{{T}^{-2}} \right]$. 

Substituting (1) and (2) in the above expression,

$\left[ E \right]=\left[ F{{A}^{-1}}{{A}^{2}}{{T}^{4}}{{T}^{-2}} \right]$ 

$\therefore \left[ E \right]=\left[ FA{{T}^{2}} \right]$

Therefore, we found the dimension of energy in powers of F, A and T to be, $\left[ FA{{T}^{2}} \right]$.

8. If Velocity, Time and Force Were Chosen as the Base Quantities, Find the Dimensions of Mass.

Ans: 

From Newton’s second law of motion, 

$\text{force}=\text{mass}\times \text{acceleration}$ 

\[\Rightarrow \text{force}=\text{mass}\times \frac{\text{Velocity}}{\text{Time}}\] 

\[\Rightarrow \frac{\text{Time}\times \text{force}}{\text{Velocity}}=\text{mass}\]

\[\Rightarrow \left[ \text{mass} \right]=\left[ \frac{FT}{V} \right]\]

\[\therefore \left[ M \right]=\left[ FT{{V}^{-1}} \right]\]

Therefore, we found the dimension of mass in terms of velocity, time and force to be \[\left[ M \right]=\left[ FT{{V}^{-1}} \right]\]. 

9. A calorie is a unit of heat or energy and is equivalent to 4.2 J where $1J=1kg{{m}^{2}}{{s}^{-2}}$. Suppose we employ a system of units in which the unit of mass equals $\alpha \text{ kg}$, the unit of length equals $\beta $ m, the unit of time is $\gamma \text{ s}$ . Show that a calorie has a magnitude $4.2{{\alpha }^{-1}}{{\beta }^{-2}}{{\gamma }^{2}}$ in terms of the new units.

Ans: 

Given that,

\[1\text{ }Calorie=4.2\left( 1kg \right)\left( 1{{m}^{2}} \right)\left( 1{{s}^{-2}} \right)\] 

New unit of mass $=\alpha \text{ kg}$ 

Hence, one kilogram in terms of the new unit, $1\text{ kg}=\frac{1}{\alpha }={{\alpha }^{-1}}$

One meter in terms of the new unit of length, $\text{1m}=\frac{1}{\beta }={{\beta }^{-1}}$  or $\text{1}{{\text{m}}^{2}}={{\beta }^{-2}}$

And, one second in terms of the new unit of time,

$1\text{ s}=\frac{1}{\gamma }={{\gamma }^{-1}}$

$1\text{ }{{\text{s}}^{2}}={{\gamma }^{-2}}$

$1\text{ }{{\text{s}}^{-2}}={{\gamma }^{2}}$

\[\therefore 1\text{ }Calorie=4.2\left( 1{{\alpha }^{-1}} \right)\left( 1{{\beta }^{-2}} \right)\left( 1{{\gamma }^{2}} \right)=4.2{{\alpha }^{-1}}{{\beta }^{-2}}{{\gamma }^{2}}\] 

10. Explain This Statement Clearly:

“To Call a Dimensional Quantity 'large' or 'small' Is Meaningless Without Specifying a Standard for Comparison”. in View of This, Reframe the Following Statements Wherever Necessary:

Ans: The given statement is true because a dimensionless quantity may be large or small, but there should be some standard reference to compare that. For example, the coefficient of friction is dimensionless but we could say that the coefficient of sliding friction is greater than the coefficient of rolling friction, but less than static friction.

A. Atoms are Very Small Objects.

Ans: An atom is very small compared to a soccer ball.

B. A Jet Plane Moves With Great Speed.

Ans: A jet plane moves with a speed greater than that of a bicycle.

C. The Mass of Jupiter Is Very Large.

Ans:  Mass of Jupiter is very large compared to the mass of a cricket ball.

D. The Air Inside This Room Contains a Large Number of Molecules.

Ans: The air inside this room contains a large number of molecules as compared to that contained by a geometry box.

E. A Proton Is Much More Massive Than an Electron.

Ans: A proton is more massive than an electron.

F. The Speed of Sound Is Much Smaller Than the Speed of Light.          

Ans:  Speed of sound is less than the speed of light.

11. Which of the Following Is the Most Precise Device for Measuring Length: 

Ans:  A device which has the minimum least count is considered to be the most precise device to measure length.

1. A vernier caliper with 20 divisions on the sliding scale.

Ans:

Least count of a vernier caliper is given by,

\[LC=1\text{ }standard\text{ }division\left( SD \right)-1\text{ }vernier\text{ }division\left( VD \right)\] 

$\Rightarrow L.C=1-\frac{9}{10}=\frac{1}{10}=0.01cm$

2. A Screw Gauge of Pitch 1 Mm and 100 Divisions on the Circular Scale

Ans:

Least count of screw gauge $=\frac{\text{Pitch}}{\text{No of divisions}}$

$\Rightarrow L.C=\frac{1}{1000}=0.001cm$

3. An Optical Instrument That Can Measure Length to Within a Wavelength of Light?

Ans: Least count of an optical device $=\text{Wavelength of light}\sim \text{1}{{\text{0}}^{-5}}cm$ 

$\Rightarrow L.C=0.00001cm$ 

Hence, among the given three options, it can be inferred that the optical instrument with the minimum least count that can measure length to within a wavelength of light is the most suitable device to measure length.

12. Answer the following:

1. You are given a thread and a meter scale. How will you estimate the diameter of the thread?

Ans: Wrap the thread on a uniform smooth rod in such a way that the coils thus formed are very close to each other. Measure the length that is wound by the thread using a metre scale. The diameter of the thread is given by the relation,

Diameter $=\frac{\text{Length of thread}}{\text{Number of turns}}$ 

2. A screw gauge has a pitch of 1.0 mm and 200 divisions on the circular scale. Do you think it is possible to increase the accuracy of the screw gauge arbitrarily by increasing the number of divisions on the circular scale?

Ans: Increasing the number of divisions of the circular scale will increase its accuracy to a negligible extent only.

3. The mean diameter of a thin brass rod is to be measured by Vernier calipers. Why is a set of 100 measurements of the diameter expected to yield a more reliable estimate than a set of 5 measurements only

Ans: A set of 100 measurements is more reliable than a set of 5 measurements because random errors involved will be reduced on increasing the number of measurements.

13. The mass of a box measured by a grocer's balance is 2.300 kg. Two gold pieces of masses 20.15 g and 20.17 g are added to the box. What is:

1. The Total Mass of the Box?

Ans: 

We are given:

Mass of grocer’s box $=2.300kg$ 

Mass of gold piece $I=20.15g=0.02015kg$ 

Mass of gold piece $II=20.17g=0.02017kg$ 

Total mass of the box $=2.3+0.02015+0.02017=2.34032kg$ 

In addition, the final result should retain as many decimal places as there are in the number with the least decimal places. Hence, the total mass of the box is $2.3kg$.

2. The Difference in the Masses of the Pieces to Correct Significant Figures?       

Ans:

Difference in masses $=20.17-20.15=0.02g$ 

During subtraction, the final result should retain as many decimal places as there are in the number with the least decimal places.

14. A physical quantity P is related to four observables $a,b,c$ and $d$ as follows:

$P=\frac{{{a}^{3}}{{b}^{2}}}{\left( \sqrt{cd} \right)}$ 

The percentage errors of measurement in $a,b,c$ and $d$ are $1%,3%,4%$ and $2%$ respectively. What is the percentage error in the quantity P? If the value of P calculated using the above relation turns out to be 3.763, to what value should you round off the result?

Ans: 

We are given the relation, 

 $P=\frac{{{a}^{3}}{{b}^{2}}}{\left( \sqrt{cd} \right)}$

The error could be calculated using the following expression, 

$\frac{\Delta P}{P}=\frac{3\Delta a}{a}+\frac{2\Delta b}{b}+\frac{1}{2}\frac{\Delta c}{c}+\frac{\Delta d}{d}$

 $\left( \frac{\Delta P}{P}\times 100 \right)%=\left( 3\times \frac{\Delta a}{a}\times 100+2\times \frac{\Delta b}{b}\times 100+\frac{1}{2}\times \frac{\Delta c}{c}\times 100+\frac{\Delta d}{d}\times 100 \right)%$

 $ =3\times 1+2\times 3+\frac{1}{2}\times 4+2$ 

 $=3+6+2+2=13%$ 

Percentage error in $P=13%$ 

Value of P is given as $3.763$.

By rounding off the given value to the first decimal place, we get $P=3.8$.

15. The unit of length convenient on the atomic scale is known as an angstrom and is denoted by \[\overset{{}^\circ }{\mathop{A}}\,\] and we know that \[\left( 1\overset{{}^\circ }{\mathop{\text{A}}}\,={{10}^{-10}}m \right)\]. The size of a hydrogen atom is about \[0.5\overset{{}^\circ }{\mathop{\text{A}}}\,\]. What is the total atomic volume in ${{m}^{3}}$ of a mole of hydrogen atoms?

Ans: 

Radius of hydrogen atom, \[r=0.5\overset{{}^\circ }{\mathop{\text{A}}}\,=0.5\times {{10}^{-10}}m\] 

Volume of hydrogen atom $V=\frac{4}{3}\pi {{r}^{3}}$ 

$\begin{align}

  & \Rightarrow V=\frac{4}{3}\times \frac{22}{7}\times {{\left( 0.5\times {{10}^{-10}} \right)}^{3}} \\ 

 & \Rightarrow V=0.524\times {{10}^{-30}}{{m}^{3}} \\ 

\end{align}$

1 mole of hydrogen contains $6.023\times {{10}^{23}}$ hydrogen atoms.

$\therefore $ Volume of 1 mole of hydrogen atoms $V'=6.023\times {{10}^{23}}\times 0.524\times {{10}^{-30}}$

$\Rightarrow V'=3.16\times {{10}^{-7}}{{m}^{3}}$ 

16. Explain This Common Observation Clearly: If You Look Out of the Window of a Fast-Moving Train, the Nearby Trees, Houses Etc. Seem to Move Rapidly in a Direction Opposite to the Train's Motion, but the Distant Objects (hill Tops, the Moon, the Stars Etc.) Seem to Be Stationary. (in Fact, Since You Are Aware That You Are Moving, These Distant Objects Seem to Move With You).         

Ans: Line-of-sight is defined as an imaginary line joining an object and an observer's eye. When we observe nearby stationary objects such as trees, houses, etc. while sitting in a moving train, they appear to move rapidly in the opposite direction because the line-of-sight changes very rapidly.

On the other hand, distant objects such as trees, stars, etc. appear stationary because of the large distance. As a result, the line-of-sight does not change its direction rapidly.

17. Precise measurements of physical quantities are a need of science. For example, to ascertain the speed of an aircraft, one must have an accurate method to find its positions at closely separated instants of time. This was the actual motivation behind the discovery of radar in World War \[\mathbf{II}\]. Think of different examples in modern science where precise measurements of length, time, mass etc. are needed. Also, wherever you can, give a quantitative idea of the precision needed.

Ans: It is indeed very true that precise measurements of physical quantities are essential for the development of science. Some examples are:

1. Ultrashort laser pulses (time interval $\sim {{10}^{-15}}s$) are used to measure time intervals in several physical and chemical processes.

2. X-ray spectroscopy is used to determine the interatomic separation or inter-planar spacing. 

3. The development of the mass spectrometer makes it possible to measure the mass of atoms precisely.

18. When the Planet Jupiter Is at a Distance of 824.7 Million Kilometers from the Earth, Its Angular Diameter Is Measured to Be $35.72''$ of Arc. Calculate the Diameter of Jupiter.

Ans:

Distance of Jupiter from the earth, $D=824.7\times {{10}^{6}}km=824.7\times {{10}^{9}}m$ 

Angular diameter $=35.72''=35.72\times 4.874\times {{10}^{-6}}rad$

Diameter of Jupiter $=d$ 

Using the relation,

\[\begin{align}

  & \theta =\frac{d}{D} \\ 

 & \Rightarrow d=\theta D=824.7\times {{10}^{9}}\times 35.72\times 4.874\times {{10}^{-6}}=143520.76\times {{10}^{3}} \\ 

 & \therefore d=1.435\times {{10}^{5}}km \\ 

\end{align}\] 

19. A LASER is a source of a very intense, monochromatic, and unidirectional beam of light. These properties of a laser light can be exploited to measure long distances. The distance of the Moon from the Earth has been already determined very precisely using a laser as a source of light. A laser light beamed at the Moon takes \[\mathbf{2}.\mathbf{56}\text{ }\mathbf{s}\] to return after reflection at the Moon's surface. How much is the radius of the lunar orbit around the Earth?

Ans: 

We are given the time taken by the laser beam to return to Earth after reflection from the moon $=2.56s$ 

We know that speed of light $=3\times {{10}^{8}}m/s$ 

Time taken by the laser beam to reach moon $=\frac{1}{2}\times 2.56=1.28s$ 

Radius of the lunar orbit = Distance between the Earth and the Moon $=1.28\times 3\times {{10}^{8}}=3.84\times {{10}^{8}}m=3.84\times {{10}^{5}}km$ 

20. A SONAR (sound navigation and ranging) uses ultrasonic waves to detect and locate objects underwater. In a submarine equipped with a SONAR the time delay between generation of a probe wave and the reception of its echo after reflection from an enemy submarine is found to be \[\mathbf{77}.\mathbf{0}\text{ }\mathbf{s}\]. What is the distance of the enemy submarine? (Speed of sound in water \[=\mathbf{1450}m{{s}^{-1}}\]).

Ans: 

Let the distance between the ship and the enemy submarine be $'S'$.

We are given,

Speed of sound in water \[=1450\text{ }m/s\] 

Time lag between transmission and reception of Sonar waves \[=77\text{ }s\] 

In this time lag, sound waves travel a distance which is twice the distance between the ship and the submarine \[\left( 2S \right)\] .

So, the time taken for the sound to reach the submarine $=\frac{1}{2}\times 77=38.5s$ 

Therefore, the distance between the ship and the submarine is given by  \[S=1450\times 38.5=55825\text{ }m=55.8\text{ }km\]

Short Questions and Answers (3 Marks Questions)

1. Just as precise measurements are necessary in Science; it is equally important to be able to make rough estimates of quantities using rudimentary ideas and common observations. Think of ways by which you can estimate the following (where an estimate is difficult to obtain, try to get an upper bound on the quantity): 

1. The Total Mass of Rain-Bearing Clouds Over India During the Monsoon. 

Ans:

For estimating the total mass of rain-bearing clouds over India during the Monsoon:

During monsoons, a meteorologist records about 215 cm of rainfall in India i.e., the height of the water column, \[h=215\text{ }cm=2.15\text{ }m\] 

We have the following information, 

Area of country, \[A=3.3\times {{10}^{12}}{{m}^{2}}\] 

Hence, the volume of rainwater, \[V=A\times h=7.09\times {{10}^{12}}{{m}^{3}}\]

Density of water, \[\rho =1\times {{10}^{3}}kg\text{ }{{m}^{-3}}\] 

We can find the mass from the given value of density and volume as,

\[M=\rho \times V=7.09\times {{10}^{15}}kg\] 

Hence, the total mass of rain-bearing clouds over India is approximately found to be  \[7.09\times {{10}^{15}}kg\].

2. The Mass of an Elephant.

Ans:

For estimating the mass of an elephant: 

Consider a ship floating in the sea whose base area is known. Measure its depth at sea (say ${{d}_{1}}$).

Volume of water displaced by the ship would be, ${{V}_{b}}=A{{d}_{1}}$ 

Now one could move an elephant on the ship and then measure the depth of the ship $\left( {{d}_{2}} \right)$. 

Let the volume of water displaced by the ship with the elephant on board be given as ${{V}_{be}}=A{{d}_{2}}$. 

Then the volume of water displaced by the elephant $=A{{d}_{2}}-A{{d}_{1}}$ .

If the density of water $=D$ 

Mass of an elephant would be $M=AD\left( {{d}_{2}}-{{d}_{1}} \right)$. 

3. The Wind Speed During a Storm.

Ans: Estimation of wind speed during a storm: 

Wind speed during a storm can be measured by using an anemometer. As wind blows, it rotates and the number of rotations in one second as recorded by the anemometer gives the value of wind speed.

4. The Number of Strands of Hair on Your Head.

Ans: Estimation of the number of strands of hair on your head:

Let the area of the head surface carrying hair be \[A\]. 

The radius of a hair can be determined with the help of a screw gauge and let it be \[r\] .

$\therefore $ Area of one hair strand $=\pi {{r}^{2}}$ 

Number of strands of hair $\approx \frac{\text{Total surface area}}{\text{Area of one hair}}=\frac{A}{\pi {{r}^{2}}}$ 

5. The Number of Air Molecules in Your Classroom.         

Ans:

Estimation of the number of air molecules in your classroom:

Let the volume of the room be \[V\].

We know that:

One mole of air at NTP occupies \[22.4\text{ }l\] i.e., $22.4\times {{10}^{-3}}{{m}^{3}}$ volume.

Number of molecules in one mole ${{N}_{A}}=6.023\times {{10}^{23}}$ (Avogadro number)

$\therefore $ Number of molecules in room of volume(V) could be found as, 

$n=\frac{6.023\times {{10}^{23}}}{22.4\times {{10}^{-3}}}\times V$  

$\Rightarrow n=134.915\times {{10}^{26}}V$

$\therefore n=1.35\times {{10}^{28}}V$

2. The unit of length convenient on the nuclear scale is a fermi: \[\mathbf{1f}={{10}^{-15}}\mathbf{m}\]. Nuclear sizes obey roughly the following empirical relation: $r={{r}_{0}}{{A}^{\frac{1}{3}}}$ , where \[\mathbf{r}\] is the radius of the nucleus, \[\mathbf{A}\] its mass number, and ${{r}_{0}}$ is a constant equal to about, \[\mathbf{1}.\mathbf{2}\text{ }\mathbf{f}\]. Show that the rule implies that nuclear mass density is nearly constant for different nuclei. Estimate the mass density of sodium nucleus and compare it with the average mass density of a sodium atom obtained in Exercise. 2.27.

Ans: 

Let r be the radius of the nucleus given by the relation,

$r={{r}_{0}}{{A}^{\frac{1}{3}}}$

${{r}_{0}}=1.2f=1.2\times {{10}^{-15}}m$

Then the volume of nucleus would be, $V=\frac{4}{3}\pi {{r}^{3}}$

\[V=\frac{4}{3}\pi {{\left( {{r}_{0}}{{A}^{\frac{1}{3}}} \right)}^{3}}=\frac{4}{3}\pi {{r}_{0}}^{3}A\] …….. (1)

Now, the mass of the nuclei M is equal to its mass number that is,

$M=A\text{ amu}=A\times 1.66\times {{10}^{-27}}kg$ 

Density of nucleus could be given by,

$\rho =\frac{\text{Mass of nucleus}}{\text{Volume of nucleus}}$ 

\[\Rightarrow \rho =\frac{A\times 1.66\times {{10}^{-27}}}{\frac{4}{3}\pi {{r}_{0}}^{3}A}=\frac{3\times 1.66\times {{10}^{-27}}}{4\pi {{r}_{0}}^{3}}kg/{{\text{m}}^{3}}\]

This relation shows that nuclear mass depends only on constant ${{r}_{0}}$. Hence, we could conclude that the nuclear mass densities of all nuclei are nearly the same.

Density of sodium nucleus could now be given by,

${{\rho }_{sodium}}=\frac{3\times 1.66\times {{10}^{-27}}}{4\times 3.14\times {{\left( 1.2\times {{10}^{-15}} \right)}^{3}}}$ 

$\Rightarrow \rho =\frac{4.98}{21.71}\times {{10}^{18}}$

$\therefore \rho =2.29\times {{10}^{17}}kg{{\text{m}}^{-3}}$

3. P.A.M. Dirac, a great physicist of this century loved playing with numerical values of fundamental constants of nature. This led him to an interesting observation that from the basic constants of atomic physics (\[c,e\], mass of electron, mass of proton) and the gravitational constant $G$ , one could arrive at a number with the dimension of time. Further, it was a very large number whose magnitude was close to the present estimate on the age of the universe (\[\sim\mathbf{15}\] billion years). From the table of fundamental constants in this book, try to see if you too can construct this number (or any other interesting number you can think of). If its coincidence with the age of the universe were significant, what would this imply for the constancy of fundamental constants?

Ans: 

One relation that consists of some fundamental constants to give the age of the Universe could be given by:

$t=\left( \frac{{{e}^{2}}}{4\pi {{\varepsilon }_{0}}} \right)\times \frac{1}{{{m}_{p}}{{m}_{e}}^{2}{{c}^{3}}G}$ 

Where,

$t=$ Age of universe

\[e=\] Charge of electrons \[=1.6\times {{10}^{-19}}C\]

${{\varepsilon }_{0}}=$ Absolute permittivity

${{m}_{p}}=$ Mass of protons $=1.67\times {{10}^{-27}}kg$

${{m}_{e}}=$ Mass of electrons $=9.1\times {{10}^{-31}}kg$

$c=$ Speed of light $=3\times {{10}^{8}}m/s$ 

$G=$ Universal gravitational constant $=6.67\times {{10}^{11}}N{{m}^{2}}k{{g}^{-2}}$

We also have,

$\frac{1}{4\pi {{\varepsilon }_{0}}}=9\times {{10}^{9}}N{{m}^{2}}/{{C}^{2}}$

Substituting all these values into the above equation, we would get,

$t=\frac{{{\left( 1.6\times {{10}^{-19}} \right)}^{4}}\times {{\left( 9\times {{10}^{9}} \right)}^{2}}}{{{\left( 9.1\times {{10}^{-31}} \right)}^{2}}\times 1.67\times {{10}^{-27}}\times {{\left( 3\times {{10}^{8}} \right)}^{3}}\times 6.67\times {{10}^{11}}}$

$\Rightarrow t=\frac{{{\left( 1.6 \right)}^{4}}\times 81}{9.1\times 1.67\times 27\times 6.67\times 365\times 24\times 3600}\times {{10}^{-76+18+62+27-24+11}}years$

$\Rightarrow t\approx 6\times {{10}^{-9}}\times {{10}^{18}}years$

$\therefore t=6\text{ billion years}$

Long Questions and Answers (4 Marks Questions)

1. A book with many printing errors contains four different formulas for the displacement $y$ of a particle undergoing a certain periodic motion:

(\[a=\]maximum displacement of the particle, $v=$ speed of the particle. $T=$ time period of motion). Rule out the wrong formulas on dimensional grounds.          

1. $y=a\sin \left( \frac{2\pi t}{T} \right)$ 

Ans: Correct.

$y=a\sin \left( \frac{2\pi t}{T} \right)$

Dimensions of $y={{M}^{0}}{{L}^{1}}{{T}^{0}}$ 

Dimensions of $a={{M}^{0}}{{L}^{1}}{{T}^{0}}$ 

Dimensions of $\sin \left( \frac{2\pi t}{T} \right)={{M}^{0}}{{L}^{0}}{{T}^{0}}$

Since the dimensions on the RHS are equal to LHS, the given formula is dimensionally correct.

2. $y=a\sin vt$ 

Ans: Incorrect.

$y=a\sin vt$

Dimensions of $y={{M}^{0}}{{L}^{1}}{{T}^{0}}$ 

Dimensions of $a={{M}^{0}}{{L}^{1}}{{T}^{0}}$ 

Dimensions of $vt={{M}^{0}}{{L}^{1}}{{T}^{-1}}\times {{M}^{0}}{{L}^{0}}{{T}^{1}}={{M}^{0}}{{L}^{1}}{{T}^{0}}$

Since the dimensions on the RHS are not equal to that of LHS, the given formula is dimensionally incorrect. 

3. $y=\left( \frac{a}{T} \right)\sin \frac{t}{a}$ 

Ans: Incorrect.

$y=\left( \frac{a}{T} \right)\sin \frac{t}{a}$ 

Dimensions of $y={{M}^{0}}{{L}^{1}}{{T}^{0}}$ 

Dimensions of $\frac{a}{T}={{M}^{0}}{{L}^{1}}{{T}^{-1}}$ 

Dimensions of $\frac{t}{a}={{M}^{0}}{{L}^{1}}{{T}^{1}}$

Since the dimensions on the RHS are not equal to LHS, the given formula is dimensionally incorrect. 

4. $y=\left( a\sqrt{2} \right)\left( \sin \frac{2\pi t}{T}+\cos \frac{2\pi t}{T} \right)$ 

Ans:  Correct.

$y=\left( a\sqrt{2} \right)\left( \sin \frac{2\pi t}{T}+\cos \frac{2\pi t}{T} \right)$ 

Dimensions of $y={{M}^{0}}{{L}^{1}}{{T}^{0}}$ 

Dimensions of \[a={{M}^{0}}{{L}^{1}}{{T}^{0}}\] 

Dimensions of $\frac{t}{T}={{M}^{0}}{{L}^{0}}{{T}^{0}}$

Since the dimensions on the RHS are equal to LHS, the given formula is dimensionally correct.

2. One mole of an ideal gas at standard temperature and pressure occupies $22.4L$ (molar volume). What is the ratio of molar volume to the atomic volume of a mole of hydrogen? (Take the size of the hydrogen molecule to be about $1\overset{{}^\circ }{\mathop{\text{A}}}\,$). Why is this ratio so large?

Ans: 

Radius of hydrogen atom, \[r=0.5\overset{{}^\circ }{\mathop{\text{A}}}\,=0.5\times {{10}^{-10}}m\] 

Volume of hydrogen atom, $V=\frac{4}{3}\pi {{r}^{3}}$ 

$\Rightarrow V=\frac{4}{3}\times \frac{22}{7}\times {{\left( 0.5\times {{10}^{-10}} \right)}^{3}}=0.524\times {{10}^{-30}}{{m}^{3}}$

Now, 1 mole of hydrogen contains $6.023\times {{10}^{23}}$ hydrogen atoms.

$\therefore $ Volume of 1 mole of hydrogen atoms, ${{V}_{a}}=6.023\times {{10}^{23}}\times 0.524\times {{10}^{-30}}=3.16\times {{10}^{-7}}{{m}^{3}}$ 

Molar volume of 1 mole of hydrogen atoms at STP,

${{V}_{m}}=22.4L=22.4\times {{10}^{-3}}{{m}^{3}}$ 

So, the required ratio would be, 

$\frac{{{V}_{m}}}{{{V}_{a}}}=\frac{22.4\times {{10}^{-3}}}{3.16\times {{10}^{-7}}}=7.08\times {{10}^{4}}$

Hence, we found that the molar volume is $7.08\times {{10}^{4}}$ times higher than the atomic volume. For this reason, the interatomic separation in hydrogen gas is much larger than the size of a hydrogen atom. 

3. The nearest star to our solar system is 4.29 light years away. How much is this distance in terms of parsecs? How much parallax would this star (named Alpha Centauri) show when viewed from two locations of the Earth six months apart in its orbit around the Sun?

Ans: 

Distance of the star from the solar system $=4.29ly$ 

1 light year is the distance travelled by light in one year.

1 light year $=\text{speed of light }\times \text{ 1 year}$ 

$1ly=3\times {{10}^{8}}\times 365\times 24\times 60\times 60=94608\times {{10}^{11}}m$ 

$\Rightarrow 4.29ly=405868.32\times {{10}^{11}}m$ 

But we have, 

$1\text{parsec}=3.08\times {{10}^{16}}m$ 

$\therefore 4.29ly=\frac{405868.32\times {{10}^{11}}}{3.08\times {{10}^{6}}}=1.32\text{parsec}$ 

We have another relation, 

$\theta =\frac{d}{D}$ 

Where,

Diameter of Earth’s orbit, $d=3\times {{10}^{11}}m$ 

Distance of star from the Earth, \[D=405868\times {{10}^{11}}m\] 

Substituting these values,

$\theta =\frac{3\times {{10}^{11}}}{405868.32\times {{10}^{11}}}=7.39\times {{10}^{-6}}rad$ 

But $1\sec =4.85\times {{10}^{-6}}rad$ 

$\therefore 7.39\times {{10}^{-6}}rad=\frac{7.39\times {{10}^{-6}}}{4.85\times {{10}^{-6}}}=1.52''$

4. Estimate the average mass density of a sodium atom assuming its size to be about $2.5\overset{{}^\circ }{\mathop{\text{A}}}\,$. (Use the known values of Avogadro's number and the atomic mass of sodium). Compare it with the density of sodium in its crystalline phase: $970kg\text{ }{{m}^{-3}}$. Are the two densities of the same order of magnitude? If so, why?        

Ans: 

Diameter of sodium atom = Size of sodium atom $=2.5\overset{{}^\circ }{\mathop{\text{A}}}\,$

Radius of sodium atom, \[r=\frac{1}{2}\times 2.5\overset{{}^\circ }{\mathop{\text{A}}}\,=1.25\overset{{}^\circ }{\mathop{\text{A}}}\,=1.25\times {{10}^{-10}}m\] 

Volume of sodium atom, $V=\frac{4}{3}\pi {{r}^{3}}$ 

$\Rightarrow V=\frac{4}{3}\times 3.14\times {{\left( 1.25\times {{10}^{-10}} \right)}^{3}}$

According to the Avogadro hypothesis, one mole of sodium contains $6.023\times {{10}^{23}}$ atoms and has a mass of \[23\text{ }g\] or $23\times {{10}^{-3}}kg$.

$\therefore $ Mass of one atom $=\frac{23\times {{10}^{-3}}}{6.023\times {{10}^{23}}}kg$

Density of sodium atom, 

$\rho =\frac{\frac{23\times {{10}^{-3}}}{6.023\times {{10}^{23}}}}{\frac{4}{3}\times 3.14\times {{\left( 1.25\times {{10}^{-10}} \right)}^{3}}}$ 

$\Rightarrow \rho =4.67\times {{10}^{-5}}kg\text{ }{{\text{m}}^{-3}}$

It is given that the density of sodium in the crystalline phase is $970kg\text{ }{{m}^{-3}}$.

Hence, the density of sodium atoms and the density of sodium in its crystalline phase are not in the same order. This is because in the solid phase, atoms are closely packed and hence the interatomic separation is very small in the crystalline phase.

5. it Is a Well-Known Fact That During a Total Solar Eclipse the Disc of the Moon Almost Completely Covers the Disc of the Sun. from This Fact and from the Information You Can Gather from Examples 2.3 and 2.4, Determine the Approximate Diameter of the Moon.  

Ans:

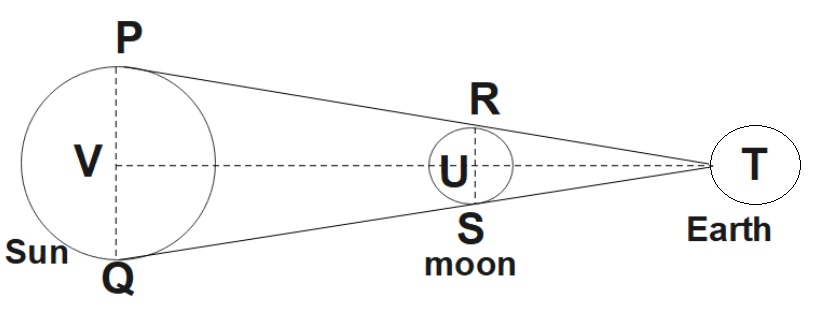
The position of the Sun, Moon, and Earth during a lunar eclipse would be as shown in the given figure.

We know that,

Distance of the Moon from the Earth $=3.84\times {{10}^{8}}m$ 

Distance of the sun from the Earth $=1.496\times {{10}^{11}}m$

Diameter of the sun $=1.39\times {{10}^{9}}m$ 

You could see that $\Delta TRS$ and $\Delta TPQ$ are similar. So, 

$\frac{1.39\times {{10}^{9}}}{RS}=\frac{1.496\times {{10}^{11}}}{3.84\times {{10}^{8}}}$

$\Rightarrow RS=\frac{1.39\times 3.84}{1.496}\times {{10}^{6}}$

$\therefore RS=3.57\times {{10}^{6}}m$

Hence, the diameter of the Moon is found to be $3.57\times {{10}^{6}}m$. 

Very Long Questions and Answers (5 Marks Questions)

1. Just as precise measurements are necessary in science; it is equally important to be able to make rough estimates of quantities using rudimentary ideas and common observations. Think of ways by which you can estimate the following (where an estimate is difficult to obtain, try to get an upper bound on the quantity): 

1. The Total Mass of Rain-Bearing Clouds Over India During the Monsoon. 

Ans: 

During monsoons, a meteorologist records about 215 cm of rainfall in India i.e., the height of the water column, \[h=215\text{ }cm=2.15\text{ }m\] 

We know,

Area of country, \[A=3.3\times {{10}^{12}}{{m}^{2}}\] 

Hence, the volume of rainwater, \[V=A\times h=7.09\times {{10}^{12}}{{m}^{3}}\]

Density of water, \[\rho =1\times {{10}^{3}}kg\text{ }{{m}^{-3}}\] 

Hence, mass of rainwater \[M=\rho \times V=7.09\times {{10}^{15}}kg\] 

Hence, the total mass of rain-bearing clouds over India is approximately found to be\[7.09\times {{10}^{15}}kg\].

2. The Mass of an Elephant.

Ans: 

Consider a ship of known base area floating in the sea. Measure its depth at sea (say ${{d}_{1}}$).

Volume of water displaced by the ship, ${{V}_{b}}=A{{d}_{1}}$.

Now, move an elephant on the ship and measure the depth of the ship $\left( {{d}_{2}} \right)$ in this case.

Volume of water displaced by the ship with the elephant on board, ${{V}_{be}}=A{{d}_{2}}$. 

Volume of water displaced by the elephant $=A{{d}_{2}}-A{{d}_{1}}$. 

Density of water $=D$ 

Mass of elephant $=AD\left( {{d}_{2}}-{{d}_{1}} \right)$ 

3. The Wind Speed During a Storm.

Ans: 

Wind speed during a storm can be measured by an anemometer. As the wind blows, it rotates. The rotation made by the anemometer in one second gives the value of wind speed.

4. The Number of Strands of Hair on Your Head.

Ans:

Area of the head surface carrying hair \[=A\] 

With the help of a screw gauge, the diameter and hence, the radius of a hair can be determined. Let it be \[r\] .

$\therefore $ Area of one hair strand$=\pi {{r}^{2}}$ 

Number of strands of hair $\approx \frac{\text{Total surface area}}{\text{Area of one hair}}=\frac{A}{\pi {{r}^{2}}}$ 

5. The Number of Air Molecules in Your Classroom.         

Ans: 

Let the volume of the room be \[V\].

One mole of air at NTP occupies \[22.4\text{ }l\] i.e., $22.4\times {{10}^{-3}}{{m}^{3}}$ volume.

Number of molecules in one mole ${{N}_{A}}=6.023\times {{10}^{23}}$ (Avogadro number)

$\therefore $ Number of molecules in room of volume(V), 

$n=\frac{6.023\times {{10}^{23}}}{22.4\times {{10}^{-3}}}\times V$ 

$\Rightarrow n=134.915\times {{10}^{26}}V$

$\therefore n=1.35\times {{10}^{28}}V$

2. The unit of length convenient on the nuclear scale is a fermi: \[\mathbf{1f}={{10}^{-15}}\mathbf{m}\]. Nuclear sizes obey roughly the following empirical relation: $r={{r}_{0}}{{A}^{\frac{1}{3}}}$ , where \[\mathbf{r}\] is the radius of the nucleus, \[\mathbf{A}\] its mass number, and ${{r}_{0}}$ is a constant equal to about, \[\mathbf{1}.\mathbf{2}\text{ }\mathbf{f}\]. Show that the rule implies that nuclear mass density is nearly constant for different nuclei. Estimate the mass density of sodium nucleus and compare it with the average mass density of a sodium atom obtained in Exercise. 2.27.

Ans: 

We know that the radius of the nucleus $r$ is given by the relation,

$r={{r}_{0}}{{A}^{\frac{1}{3}}}$

${{r}_{0}}=1.2f=1.2\times {{10}^{-15}}m$

Volume of nucleus, $V=\frac{4}{3}\pi {{r}^{3}}$

\[V=\frac{4}{3}\pi {{\left( {{r}_{0}}{{A}^{\frac{1}{3}}} \right)}^{3}}=\frac{4}{3}\pi {{r}_{0}}^{3}A\] …….. (1)

Now, the mass of the nuclei $M$ is equal to its mass number i.e.,

$M=A\text{ amu}=A\times 1.66\times {{10}^{-27}}kg$ 

Density of nucleus,

$\rho =\frac{\text{Mass of nucleus}}{\text{Volume of nucleus}}$ 

\[\Rightarrow \rho =\frac{A\times 1.66\times {{10}^{-27}}}{\frac{4}{3}\pi {{r}_{0}}^{3}A}=\frac{3\times 1.66\times {{10}^{-27}}}{4\pi {{r}_{0}}^{3}}kg/{{\text{m}}^{3}}\]

This relation shows that nuclear mass depends only on constant ${{r}_{0}}$. Hence, the nuclear mass densities of all nuclei are nearly the same.

Density of sodium nucleus could be given by,

${{\rho }_{sodium}}=\frac{3\times 1.66\times {{10}^{-27}}}{4\times 3.14\times {{\left( 1.2\times {{10}^{-15}} \right)}^{3}}}$ 

$\Rightarrow \rho =\frac{4.98}{21.71}\times {{10}^{18}}$

$\therefore \rho =2.29\times {{10}^{17}}kg{{\text{m}}^{-3}}$

3. P.A.M. Dirac, a great physicist of this century loved playing with numerical values of fundamental constants of nature. This led him to an interesting observation that from the basic constants of atomic physics (\[c,e\], mass of electron, mass of proton) and the gravitational constant $G$ , one could arrive at a number with the dimension of time. Further, it was a very large number whose magnitude was close to the present estimate on the age of the universe (\[\sim\mathbf{15}\] billion years). From the table of fundamental constants in this book, try to see if you too can construct this number (or any other interesting number you can think of). If its coincidence with the age of the universe were significant, what would this imply for the constancy of fundamental constants?

Ans: 

One relation that is consisting of some fundamental constants to give the age of the Universe could be given by:

$t=\left( \frac{{{e}^{2}}}{4\pi {{\varepsilon }_{0}}} \right)\times \frac{1}{{{m}_{p}}{{m}_{e}}^{2}{{c}^{3}}G}$ 

Where,

$t=$ Age of universe

\[e=\] Charge of electrons \[=1.6\times {{10}^{-19}}C\]

${{\varepsilon }_{0}}=$ Absolute permittivity

${{m}_{p}}=$ Mass of protons $=1.67\times {{10}^{-27}}kg$

${{m}_{e}}=$ Mass of electrons $=9.1\times {{10}^{-31}}kg$

$c=$ Speed of light $=3\times {{10}^{8}}m/s$ 

$G=$ Universal gravitational constant $=6.67\times {{10}^{11}}N{{m}^{2}}k{{g}^{-2}}$

Also,

$\frac{1}{4\pi {{\varepsilon }_{0}}}=9\times {{10}^{9}}N{{m}^{2}}/{{C}^{2}}$

Substituting all these values in the above equation, we get,

$t=\frac{{{\left( 1.6\times {{10}^{-19}} \right)}^{4}}\times {{\left( 9\times {{10}^{9}} \right)}^{2}}}{{{\left( 9.1\times {{10}^{-31}} \right)}^{2}}\times 1.67\times {{10}^{-27}}\times {{\left( 3\times {{10}^{8}} \right)}^{3}}\times 6.67\times {{10}^{11}}}$

$\Rightarrow t=\frac{{{\left( 1.6 \right)}^{4}}\times 81}{9.1\times 1.67\times 27\times 6.67\times 365\times 24\times 3600}\times {{10}^{-76+18+62+27-24+11}}years$

$\Rightarrow t\approx 6\times {{10}^{-9}}\times {{10}^{18}}years$

$\therefore t=6\text{ billion years}$

4. Write S.I. Units of Luminous Intensity and Temperature.

Ans:  S.I unit of luminous intensity is candela and is represented by \[cd\]. The SI unit of temperature is kelvin and is represented by $K$.

5. A New Unit of Length Is Chosen Such That the Speed of Light in Vacuum Is Unity. What Is the Distance Between the Sun and the Earth in Terms of the New Unit If Light Takes 8 Min and 20 s to Cover This Distance?

Ans: 

Distance between the Sun and the Earth is given by:

\[\text{x= Speed of light}\times \text{Time taken by light to cover the distance}\] 

We are given, in the new unit, the speed of light, \[c=1\text{ }unit\]. 

Time taken, \[t=8\text{ }min\text{ }20\text{ }s=500\text{ }s\] 

$\therefore $ Distance between the Sun and the Earth \[x'=c\times t'=1\times 500=500\text{ }units\]. 

6. A student measures the thickness of a human hair using a microscope of magnification 100. He makes 20 observations and finds that the average width of the hair in the field of view of the microscope is 3.5 mm. Estimate the thickness of hair.

Ans:

We are given: 

Magnification of the microscope \[=100\] 

Average width of the hair in the field of view of the microscope \[=3.5\text{ }mm\] 

$\therefore $ Actual thickness of the hair would be, $\frac{3.5}{100}=0.035\text{ }mm.$ 

7. The photograph of a house occupies an area of $1.75c{{m}^{2}}$  on a 35 mm slide. The slide is projected onto a screen, and the area of the house on the screen is $1.55{{m}^{2}}$. What is the linear magnification of the projector-screen arrangement?

Ans: 

We are given, 

The area of the house on the 35mm slide is found to be, ${{A}_{O}}=1.75c{{m}^{2}}$.

The area of the image of the house that is formed on the screen, ${{A}_{I}}=1.55{{m}^{2}}=1.55\times {{10}^{4}}c{{m}^{2}}$.

We know that areal magnification is given by, 

${{m}_{a}}=\frac{{{A}_{I}}}{{{A}_{O}}}$

Substituting the given values, 

${{m}_{a}}=\frac{1.55\times {{10}^{4}}}{1.75}$

Now, we have the expression for linear magnification as, ${{m}_{l}}=\sqrt{{{m}_{a}}}$ 

$\Rightarrow {{m}_{l}}=\sqrt{\frac{1.55}{1.75}\times {{10}^{4}}}$ 

$\therefore {{m}_{l}}=94.11$

Thus, we found the linear magnification in the given case to be, ${{m}_{l}}=94.11$.

8. The farthest objects in our Universe discovered by modern astronomers are so distant that light emitted by them takes billions of years to reach the Earth. These objects (known as quasars) have many puzzling features, which have not yet been satisfactorily explained. What is the distance (in km) of a quasar from which light takes 3.0 billion years to reach us?    

Ans: 

We are given, time taken by quasar light to reach Earth, \[t=3\text{ }billion\text{ }years\]. 

That is,

$\Rightarrow t=3\times {{10}^{9}}years$ 

$\Rightarrow t=3\times {{10}^{9}}\times 365\times 24\times 60\times 60s$

We know that,

Speed of light, $c=3\times {{10}^{8}}m/s$ 

Distance between the Earth and quasar,

$x=c\times t$

$\Rightarrow x=\left( 3\times {{10}^{8}} \right)\times \left( 3\times {{10}^{9}}\times 365\times 24\times 60\times 60 \right)$

$\Rightarrow x=283824\times {{10}^{20}}m$

$\therefore x=2.8\times {{10}^{22}}km$

Therefore, we found the distance (in km) of a quasar from which light takes 3.0 billion years to reach us to be $x=2.8\times {{10}^{22}}km$.

Chapter 1 Physics Class 11 Important Questions – PDF Download

Class 11 Physics Ch 1 important questions are easily available on Vedantu website in an easy and free download PDF version. The set of questions are useful for the revision and practice of the students. They brief the students with the type of questions asked in the examinations, how to handle all the questions, and get an enhanced practice for all the topics and sub-topics involved in the curriculum.

CBSE class 11th is a comparatively more challenging section, and the entire syllabus of the class is more challenging. The students must get an extra load of a practice resource to get a crystal clearance of all the concepts and know different ways of tackling and solving various problems. Using the PDF version of the CBSE class 11 physics chapter 1 important questions serves the purpose best and assists all the students during their preparations and whenever they require more study and revision resources.

Physics Class 11 Ch 1 Important questions are available in free download PDF version on Vedantu, making sure that every student can access it quickly and whenever required. Furthermore, there is no device limitation for accessing the questions, and the students can practice for their examinations whenever they wish to do so. Class 11 Physics Chapter 1 extra questions contain a list of problems and the solutions for them, making sure that the students are not required to have such multiple resources whenever they are stuck.

Important Questions for Class 11 Physics Chapter 1 – Related Essential Concepts

There are several topics associated with the syllabus from which the questions are asked in the examinations. Here are some essential concepts related to the Units and Measurement Class 11 important concepts.

Unit and S.I. Unit

Unit is the measuring term for the different types of quantities. The most common systems of the unit for measuring any quantity are as follows:

1. S.I. System

2. FPS system

3. CGS system

4. MKS system

S.I. unit is the international measuring system, used universally for the scientific and technical research to avoid confusion. This is the standard measuring system and is useful because it helps the entire World understand the measurements in a single unit system. Physics has different quantity measurements, and thus other S.I. units. 

The Quantities Mainly Group As

1. S.I. Base Unit – Base unit is the fundamental unit and the building block of any system. They are used for deriving the other units—for example, Kilogram.

2. S.I. Derived Unit – The units derived from the base units are known as S.I. derived units.

Distance and Its Units

Distance is the measurement of the path that a body covers between the initial and the final positions. It is the result of the product of speed and time, and is represented as:

D = S * T. Here,

1. D is the distance that the body travelled; its unit is metre.

2. T is the time that the body took for covering the said distance; its unit is second.

3. S is the speed with which the body covered the said distance; its unit is metre /second.

The most commonly used units are Kilometre, Metre, Centimetre, and millimetre for measuring the distance.

Mass and Weight

Mass means the amount of matter present in an object. It is the intrinsic quantity of anybody and helps find out the parameters dependent on the mass. It helps determine the strength of the object's gravitational attraction concerning the other bodies, the item's resistance to acceleration due to any force, inertia, and many more. It also helps in deriving the Theory of Relativity, using E = mc2.

Weight of the body is different from its mass. It refers to the force exerted over the mass of anybody due to the gravitational pull. Mass is the universal measurement, but the body's weight is varying, as it depends on the gravity of the planet. It is described as W = mg.

Atomic Mass Unit

The Atomic Mass unit is helpful while dealing with the smaller atoms and molecules with tiny mass such that measuring them in Kilogram gets a lot inconvenient. One atomic mass unit refers to the 1/ 12th of the mass of the C-12 Carbon atom. It is equal to 1.22 x 10-27.

Other Important Concepts Related to CBSE Class 11 Physics Chapter 1 Important Questions

Apart from these concepts, there are many other important topics involved in Chapter Units and Measurements. Time measurement is also included in the chapter. The unit also contains the study of various measurement errors, like absolute error, relative error, random error, systematic error, and gross error. All the concepts carry some questions of different marks in the examinations and are essential for both school curriculum and practice for the competitive level exams.

Important Questions for Class 11 Physics Chapter 1

Practising the questions enhances the practice for the concepts and makes the students confident about them. Here is the list of top ten problems from the set of Units and Measurements Class 11 important questions:

1. Differentiate between A0 and A.U.

2. What is the S.I. unit of a solid angle?

3. Mention the physical quantities having the S.I. unit as Pascal and electron volt.

4. Suppose there is a planet X which is at a distance of 824.7 kilometres from Earth. The angular diameter of planet X is 35.7211 arcs. Calculate the diameter of the planet X.

5. There is a radar signal that beams towards the planet X from the Earth, and then the echo for the same is received after seven minutes. Calculate the signal's velocity, if we have the distance between the Earth and the planet X to be 6.3 x 1010 m.

6. Calculate the dimensions of the specific heat and the latent heat.

7. G, E, m, and l denote Gravitational constant, Energy, mass, and angular momentum, respectively. Determine the dimension for the given term: El2 / m3G2.

8. Calculate the maximum time that a light beam will take to pass through a nucleus of diameter 1.56 x 10-16 m. (The speed of light is 3 x 108 m/s).

9. If we chose the time, force, and velocity as the basic quantities, calculate the dimension of mass accordingly.

10. A calorie refers to the standard unit of energy or heat and is equal to 4.2 Joules. Here, 1J = 1 Kg m2 / s2. Suppose we get a unit system where the mass unit is equal to a kg, and length equals to bm, the time is ys. Now show that the magnitude of a calorie is 4.2 a-1 b-2 y2, according to the new units taken.

Benefits of Important Questions for Class 11 Physics Chapter 1

The set of Class 11 Physics Chapter 1 important questions are very important for the students' preparation and practice and help them pass the examinations with flying colours. Here are some key benefits of having the set of important questions handy:

1. Important questions for Class 11 Physics Chapter 1 are essential as they provide the practice material for all the types of questions to the students, thus helping them be confident while attempting the examinations' questions.

2. Class 11 Physics Chapter 1 extra questions provide the students with a brief idea about the various problem sets asked in the questions and multiple approaches to solving them.

3. The experts of Vedantu explicitly design the question set, and thus the solutions are available in an easily understandable language and with sufficient sets of explanations.

Important Related Links for CBSE Class 11 

Conclusion

The Class 11 Physics Chapter 1 Units and Measurements is an essential chapter that lays the foundation for the study of Physics. It introduces students to the fundamental concepts of measurements, units, and dimensions, which are crucial for understanding the laws of Physics. The chapter covers topics such as the International System of Units (SI), dimensional analysis, significant figures, and errors in measurements. Students should pay close attention to this chapter and practice solving numerical problems to gain a thorough understanding of the concepts. Vedantu provides comprehensive study materials, including notes, sample papers, and solutions to previous year question papers, to help students prepare for their exams. By mastering the concepts covered in this chapter, students can build a strong foundation for their future studies in Physics and related fields.