




Difference Between Ideal and Non-Ideal Solutions (With Examples)
In Chemistry, understanding ideal and non-ideal solutions is essential for JEE Main. These terms describe how real mixtures of substances behave compared to theoretical expectations. Ideal solutions follow specific rules, while non-ideal solutions deviate due to molecular interactions. Recognising these differences simplifies numericals and MCQs related to Raoult’s Law and colligative properties, frequent in the JEE syllabus.
Introduction to Solutions
A solution is a homogeneous mixture of two or more substances at the molecular level. The major component is called the solvent, and the substance dissolved is the solute. Solutions are classified based on the state of components and their behaviour — leading to the key concepts of ideal solutions and non-ideal solutions.
Ideal Solutions: Definition, Characteristics, and Examples
An ideal solution is one that obeys Raoult’s Law across all concentrations. In such mixtures, the interaction strength between A and B molecules (A-B) equals those between A-A and B-B. Ideal solutions show no enthalpy change (ΔHmix=0) or volume change (ΔVmix=0) on mixing.
- Obeys Raoult’s Law at all compositions.
- No heat is absorbed or evolved when mixed (ΔHmix=0).
- No change in volume on mixing (ΔVmix=0).
- Similar size and intermolecular forces between components.
- Examples: benzene & toluene, hexane & heptane.
The key to ideal behaviour is the equivalence of chemical nature and physical properties among components. In practice, simple hydrocarbons (e.g. benzene-toluene) approach this ideality, making them classic textbook examples.
Representing the interaction of Solution molecules visually can help conceptualise this behaviour in the molecular context.
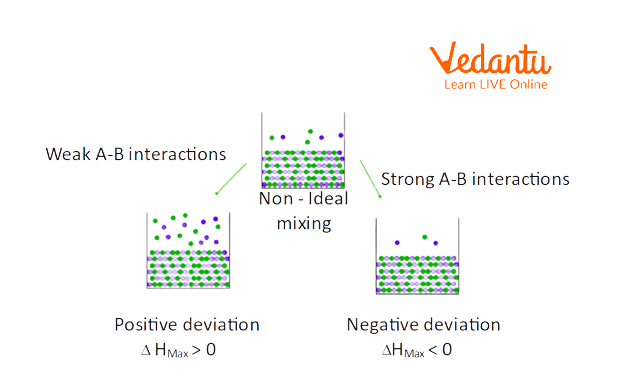
Non-Ideal Solutions: Types, Deviations, and Real-World Cases
Non-ideal solutions do not obey Raoult’s Law throughout the entire concentration range. Here, intermolecular forces between different molecules (A-B) are either stronger or weaker than those in pure components, leading to energy and volume changes when mixed. Non-ideal solutions are far more common in the laboratory and industry.
- Show ΔHmix ≠ 0 or ΔVmix ≠ 0.
- Vapour pressure deviates from linearity (Raoult’s Law).
- Exhibit positive or negative deviation from Raoult’s Law:
- Positive deviation: Weaker A-B interaction (e.g. ethanol-water).
- Negative deviation: Stronger A-B interaction (e.g. acetone-chloroform).
- Colloquially called “real solutions”.
- Examples: ethanol & water (positive); acetone & chloroform (negative).
Positive deviation means the solution has higher vapour pressure than predicted (likes repel more, less attraction); negative deviation results in lower vapour pressure (stronger attraction, less escape tendency).
Difference Between Ideal and Non-Ideal Solutions
| Property | Ideal Solution | Non-Ideal Solution |
|---|---|---|
| Raoult’s Law | Obeyed throughout | Deviated (positive/negative) |
| Enthalpy Change (ΔHmix) | Zero | Not zero |
| Volume Change (ΔVmix) | Zero | Not zero |
| Molecular Interaction | Similar (A-B ≈ A-A, B-B) | Different (A-B ≠ A-A, B-B) |
| Examples | Benzene–Toluene, Hexane–Heptane | Ethanol–Water, Acetone–Chloroform |
The most direct way to distinguish is by checking compliance with Raoult’s Law and observing energy or volume change during mixing.
Chemical Potential and Raoult’s Law in Solutions
The chemical potential (μ) is a measure of the “escaping tendency” of molecules. For ideal solutions, μ for component i is given by:
μi = μi* + RT ln xi
where xi is mole fraction and μi* is standard chemical potential. In non-ideal solutions, activity (ai) replaces xi, and “activity coefficients” become relevant. In calculations, deviations from Raoult’s Law signal non-ideality, requiring more complex corrections.
- Raoult’s Law: pi = xipi*
- Total vapour pressure is the sum of partial pressures (simple in ideal, complex in non-ideal solutions).
For JEE numericals, assume ideality unless the question hints otherwise or gives enthalpy/volume data or asks about deviation types.
Memorable Examples and Applications
- Benzene + Toluene (ideal solution example) mix with no volume/heat change.
- Ethanol + Water: Non-ideal, positive deviation; solution gets warmer, vapour pressure rises.
- Acetone + Chloroform: Non-ideal, negative deviation; solution cools (exothermic), vapour pressure drops.
- Raoult’s Law numericals often directly test identification of ideality/non-ideality.
- Real-world: Industrial distillation must account for non-ideal behaviour (azeotropes, ethanol-water separation).
- MCQs may ask: “Which mixture will have maximum deviation from Raoult’s Law?”
JEE Exam MCQs: Sample Applications
- Which of the following is an ideal solution pair? (A) Ethanol-water (B) Benzene-toluene (C) Acetone-chloroform (D) H2O-H2SO4
Correct answer: (B) - Positive deviation from Raoult’s Law occurs when:
(A) Unlike interactions are stronger (B) Like interactions are stronger (C) Molecules escape easily (D) Solution absorbs heat
Correct answer: (C), (D) - Solutions Mock Test 3 contains practice questions on this topic for further self-assessment.
Quick Revision Table: Key Differences
| Aspect | Ideal Solution | Non-Ideal Solution |
|---|---|---|
| Raoult’s Law | Obeyed | Not obeyed |
| Energy/Volume Change | No change | Change occurs |
| Intermolecular Forces | Similar | Dissimilar |
| Examples | Benzene–toluene | Ethanol–water |
Use these tables for rapid JEE revision before tests. Focus especially on examples and deviations, as MCQs often target these.
Further Reading and Recommended Vedantu Links
- Raoult’s Law and Its Applications for deeper theory.
- Types of Solutions in Chemistry to strengthen basics.
- Solutions - Introduction & Properties for overall context.
Mastering ideal and non-ideal solutions gives a scoring edge in Chemistry. Regular practice with Vedantu’s resources and real-world examples sharpens both theory and numericals for the JEE Main exam.
FAQs on Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry
1. What are ideal and non-ideal solutions?
Ideal solutions follow Raoult's Law at all concentrations and show no enthalpy or volume change upon mixing, while non-ideal solutions deviate from these behaviors.
Key points:
- Ideal solutions: Obey Raoult’s Law, ΔHmix = 0, ΔVmix = 0
- Non-ideal solutions: Show either positive or negative deviation, with a change in enthalpy and/or volume
- Examples: Benzene-toluene (ideal), ethanol-water (non-ideal)
2. What is an example of a non-ideal solution?
A common example of a non-ideal solution is a mixture of ethanol and water.
Key points:
- Shows positive deviation from Raoult’s Law, as molecules interact less strongly
- Vapor pressure is higher than predicted for ideal behavior
- Other non-ideal examples: acetone-chloroform (negative deviation), HCl-water
3. What is the ideal solution and its example?
An ideal solution is one where the components follow Raoult’s Law throughout all concentrations.
Key points:
- No enthalpy or volume change on mixing (ΔHmix = 0, ΔVmix = 0)
- Examples: benzene-toluene, n-hexane-n-heptane
- For such pairs, intermolecular forces between like and unlike molecules are nearly the same
4. What is the differentiation between ideal and non-ideal?
The main difference is that ideal solutions obey Raoult’s Law, with no heat or volume change, while non-ideal solutions show deviations and have changes in energy and/or volume.
Summary difference:
- Ideal: Raoult’s Law obeyed, no ΔH or ΔV
- Non-ideal: Raoult’s Law not followed, ΔH and/or ΔV ≠ 0
- Examples: Ideal – benzene + toluene; Non-ideal – ethanol + water
5. What are the main differences between ideal and non-ideal solutions?
The main differences between ideal and non-ideal solutions are:
- Raoult’s Law: Ideal obey it at all concentrations, non-ideal do not
- Enthalpy of mixing (ΔHmix): Zero for ideal, non-zero for non-ideal
- Volume change (ΔVmix): Zero for ideal, non-zero for non-ideal
- Nature of interactions: Same (ideal), stronger or weaker (non-ideal)
- Examples: Benzene-toluene (ideal), ethanol-water (non-ideal)
6. What is Raoult's Law and how is it related to ideal solutions?
Raoult's Law states that the vapor pressure of a component in a solution is proportional to its mole fraction and its pure vapor pressure.
Relation to ideal solutions:
- Ideal solutions obey Raoult's Law at all compositions
- Expressed as Psolution = XAPA0 + XBPB0
- Any deviation signals non-ideal behavior
7. Why do some solutions show positive or negative deviation from Raoult’s Law?
Solutions deviate from Raoult’s Law when attractions between unlike molecules differ from those between like molecules.
- Positive deviation: Weaker A-B interactions, higher vapor pressure (e.g., ethanol-water)
- Negative deviation: Stronger A-B interactions, lower vapor pressure (e.g., acetone-chloroform)
- This influences properties like boiling/freezing points and solution energetics
8. Can a solution be perfectly ideal in real life?
Truly ideal solutions are theoretical, but real mixtures like benzene-toluene behave nearly ideal under certain conditions.
- Exact ideal behavior is rare because all molecules interact to some degree
- Most real solutions are non-ideal, especially at higher concentrations
9. How do intermolecular forces influence solution ideality?
Intermolecular forces determine whether a solution acts ideal or non-ideal.
- Ideal: A-A, B-B, and A-B forces are equal
- Non-ideal: A-B forces are stronger (negative deviation) or weaker (positive deviation) than like molecules
- This affects mixing behavior, enthalpy, and vapor pressure
10. Can you list some examples of ideal and non-ideal solutions?
Yes, here are some common examples:
Ideal solutions:
- Benzene & Toluene
- n-Hexane & n-Heptane
- Chlorobenzene & Bromobenzene
- Ethanol & Water (positive deviation)
- Acetone & Chloroform (negative deviation)
- Hydrochloric acid & Water
11. State any four differences between ideal and non-ideal solutions.
Four main differences between ideal and non-ideal solutions:
- 1. Raoult’s Law: Obeyed by ideal, deviated in non-ideal
- 2. Enthalpy Change (ΔH): Zero for ideal, not zero for non-ideal
- 3. Volume Change (ΔV): Zero for ideal, non-zero for non-ideal
- 4. Nature of Intermolecular Forces: Same in ideal, different in non-ideal
12. Is the concept of ideal solutions similar to ideal gases?
Ideal solutions and ideal gases are similar in that they both assume no interaction energy changes between constituents.
- Both are theoretical models for simplifying calculations
- Ideal gases ignore intermolecular forces entirely; ideal solutions require A-A, B-B, and A-B forces to be equal
- In real systems, deviations occur in both cases

































