




Step-by-Step Derivation of the Electric Field at a Point on the Axis
The electric field due to a uniformly charged ring is a fundamental topic in electrostatics, critical for understanding the behavior of charge distributions with axial symmetry. This concept provides essential insight for JEE Main and other competitive exams, where analytical derivation and application of formulas are frequently tested.
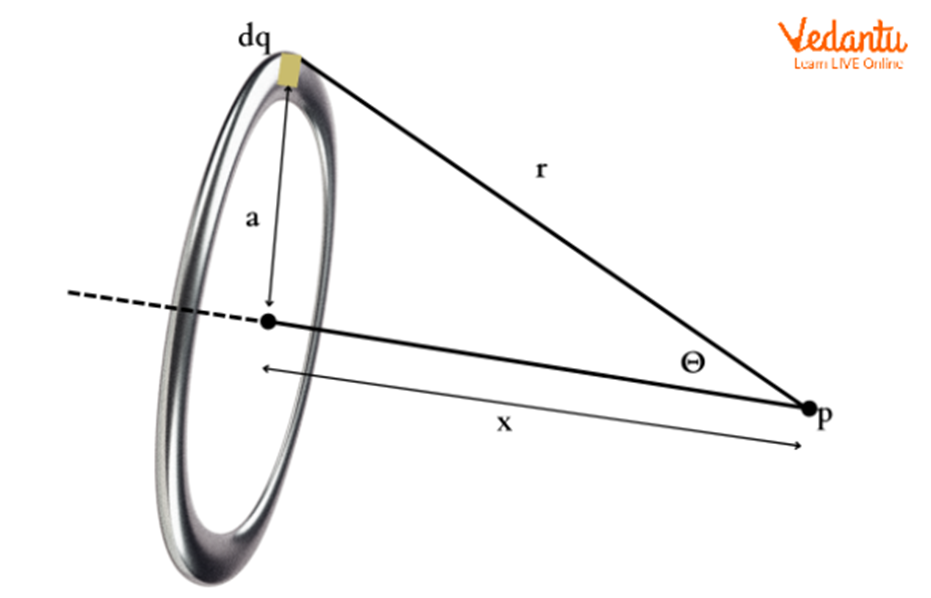
Definition and Physical Model of a Uniformly Charged Ring
A uniformly charged ring consists of a thin circular wire of radius $R$, carrying total charge $Q$ distributed uniformly along its circumference. The study of its electric field focuses on points along the axis perpendicular to the plane of the ring that passes through its center.
This setup forms the basis for analyzing the net electric field due to continuous charge distributions with circular symmetry. Such fields often serve as building blocks in more complex electrostatic arrangements, enabling superposition techniques. For related symmetry concepts, refer to Electrostatics Overview.
Derivation of Electric Field on the Axis of a Uniformly Charged Ring
Consider a ring of radius $R$ with total charge $Q$ and linear charge density $\lambda = \dfrac{Q}{2\pi R}$. Let $P$ be a point located on the axis at a distance $x$ from the center of the ring.
Take a small length element $dl$ of the ring. The charge on this element is $dq = \lambda\, dl$. By Coulomb’s law, the electric field due to $dq$ at point $P$ is directed along the line joining $dq$ and $P$.
The distance from $dq$ to point $P$ is $r = \sqrt{R^2 + x^2}$. Therefore, the magnitude of the electric field due to $dq$ at $P$ is
$dE = \dfrac{1}{4\pi\varepsilon_0} \dfrac{dq}{(R^2 + x^2)}$
Due to symmetry, the horizontal (radial) components of $dE$ from opposite elements cancel. Only the axial components contribute to the net field at $P$.
The axial component is $dE_x = dE \cos\theta$, where $\cos\theta = \dfrac{x}{\sqrt{R^2 + x^2}}$.
Therefore,
$dE_x = \dfrac{1}{4\pi\varepsilon_0} \dfrac{\lambda\, dl}{R^2 + x^2} \dfrac{x}{\sqrt{R^2 + x^2}}$
Integrate $dE_x$ over the entire ring to get the total electric field at point $P$:
$E = \int dE_x = \dfrac{1}{4\pi\varepsilon_0} \dfrac{\lambda x}{(R^2 + x^2)^{3/2}} \int dl$
$ \int dl $ over the full ring equals the circumference, $2\pi R$. Substitute $\lambda = Q/2\pi R$ to obtain:
$E = \dfrac{1}{4\pi\varepsilon_0} \cdot \dfrac{Q x}{(R^2 + x^2)^{3/2}}$
This result gives the magnitude of the electric field at a point on the axis a distance $x$ from the center. The direction is along the axis, away from the ring for positive $Q$ and towards the ring for negative $Q$.
Special Cases of the Electric Field Due to a Uniformly Charged Ring
Several important results can be obtained by analyzing special cases of the axial field formula.
| Scenario | Electric Field $E$ |
|---|---|
| At center ($x=0$) | $0$ |
| At far axial point ($x \gg R$) | $\dfrac{1}{4\pi\varepsilon_0} \dfrac{Q}{x^2}$ |
| At maximum field | $x = \dfrac{R}{\sqrt{2}}$ |
At the center, symmetry ensures perfect cancellation of the fields due to all elements. When $x \gg R$, the ring appears as a point charge and the field reduces to the standard Coulomb's law result. For maximum field, differentiate $E$ with respect to $x$ and solve for the extremum.
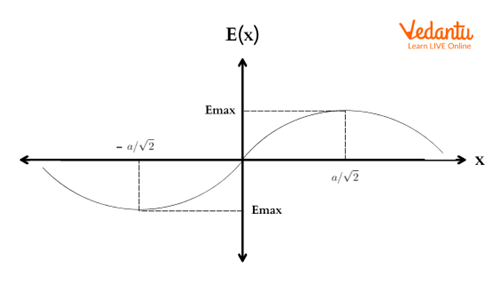
Graphical Representation of Electric Field Along the Axis
The graph of electric field $E$ versus position $x$ along the axis is a bell-shaped curve, with $E=0$ at the center, rising to a maximum, and decreasing as $x^{-2}$ for large $x$. This illustrates the dependence of the field strength both near and far from the ring.
Comparison with Other Charge Distributions
The field from a uniformly charged ring is distinct from that due to linear, planar, or volumetric charge distributions. For example, an infinite wire produces a radially symmetric field, whereas a charged disc generates nonzero axial fields at its center. For details on field lines and symmetry, see Electric Field Lines Properties.
| Distribution | Key Field Equation |
|---|---|
| Uniformly charged ring | $E = \dfrac{1}{4\pi\varepsilon_0}\dfrac{Qx}{(R^2+x^2)^{3/2}}$ |
| Infinite straight wire | $E = \dfrac{\lambda}{2\pi\varepsilon_0 r}$ |
| Disc (center) | Nonzero, depends on radius and position |
Applications of the Electric Field Due to a Uniformly Charged Ring
The electric field produced by a uniformly charged ring finds use in analytical models, particle accelerators, and cathode ray tubes. Ring fields also serve as reference cases for superposition problems and are foundational for understanding complex field configurations in electrostatics.
In devices such as cyclotrons and focusing systems, accurate knowledge of ring fields enables precise control over charged particle motion. For further reading on related potentials and applications, refer to Understanding Electric Potential.
Key Formulas and Results Summary
- Axial field: $E = \dfrac{1}{4\pi\varepsilon_0} \dfrac{Qx}{(R^2 + x^2)^{3/2}}$
- Field at center: $E = 0$
- Far field: $E \rightarrow \dfrac{1}{4\pi\varepsilon_0} \dfrac{Q}{x^2}$
- Direction is always along axis
Solved Example: Electric Field on Axis of a Ring
A ring has radius $0.5\,\text{m}$ and charge $Q=2\times10^{-6}\,\text{C}$. Calculate the field at a point on its axis $0.6\,\text{m}$ from the center.
Substitute $R=0.5\,\text{m}$, $x=0.6\,\text{m}$, $Q=2\times10^{-6}\,\text{C}$:
$E = \dfrac{1}{4\pi\varepsilon_0} \cdot \dfrac{Qx}{(R^2+x^2)^{3/2}}$
Calculate $(0.5^2+0.6^2)^{3/2} = (0.25+0.36)^{3/2} = (0.61)^{3/2} \approx 0.476$
$E = 9 \times 10^{9} \cdot \dfrac{2 \times 10^{-6} \times 0.6}{0.476}$
$E \approx 9 \times 10^{9} \cdot \dfrac{1.2 \times 10^{-6}}{0.476}$
$E \approx 9 \times 10^{9} \cdot 2.52 \times 10^{-6}$
$E \approx 22,680\,\text{N/C}$, directed along the axis away from the ring (for positive charge).
Conceptual Notes and Additional Observations
The electric field due to a uniformly charged ring cannot be determined using Gauss's Law, as the required symmetry is absent. The derivation relies on Coulomb’s Law and vector addition of differential contributions.
For non-uniform charge distributions, the field calculation requires recalculation of $dq$ as a function of angle and subsequent integration. Ensure clear understanding of both symmetry and calculus for JEE Main success.
Further study of field distributions aids in analysis of capacitors and electrostatic measuring instruments. Detailed concepts may be explored in Understanding Capacitors and Galvanometer Functionality.
FAQs on Understanding the Electric Field of a Uniformly Charged Ring
1. What is the electric field at a point on the axis of a uniformly charged ring?
The electric field on the axis of a uniformly charged ring at a distance x from the center is given by:
- The formula: E = (1/4πε0) × (qx) / (x2 + a2)3/2, where q is the total charge and a is the ring’s radius.
- The field is directed along the axis of the ring.
- The electric field is zero at the center and maximum at a certain point along the axis.
2. How do you derive the expression for electric field due to a charged ring at a point on its axis?
To derive the electric field on the axis of a uniformly charged ring:
- Consider a ring of radius a with total charge q.
- Let the point of interest be at distance x from the center on the axis.
- Divide the ring into infinitesimal charge elements, calculate the field due to each, and use symmetry.
- Components perpendicular to the axis cancel, while axial components add up.
- The result is E = (1/4πε0) × (q x) / (x2 + a2)3/2.
4. What is the direction of the electric field due to a uniformly charged ring at a point on its axis?
The direction of the electric field at a point on the axis of a uniformly charged ring is:
- Along the axis of the ring – pointing away from the ring's center if the charge is positive, or towards if negative.
- This is due to symmetry; transverse components cancel out.
5. What is the value of the electric field at the center of a uniformly charged ring?
The electric field at the center of a uniformly charged ring is zero.
- This is because the contributions from all infinitesimal charge elements around the ring cancel each other due to symmetry.
6. Why does the electric field at the center of a ring become zero?
The electric field at the center is zero because:
- Each charge element has an equal and opposite counterpart on the ring.
- Their electric field vectors at the center cancel out entirely due to symmetry.
7. How do you calculate the electric field due to a uniformly charged ring at an off-axis point?
The calculation for the electric field at an off-axis point is complex:
- Generally, it involves resolving the contribution from each charge element using vector addition.
- Direct analytical expressions are rarely possible; integration in three dimensions is needed.
- Numerical methods are typically used for precise calculation at off-axis points.
8. What are the uses or applications of the electric field due to a ring?
The electric field due to a ring finds applications in:
- Designing particle accelerators and electron beam devices.
- Understanding the behavior of charged particle traps.
- Analyzing field patterns in cyclic symmetry for engineering and physics experiments.
9. How do you find the potential due to a uniformly charged ring at a point on its axis?
The electric potential at a point on the axis of a uniformly charged ring is:
- V = (1/4πε0) × q / √(x2 + a2)
- Here, q is total charge, a is radius, and x is distance from center on the axis.
10. What happens to the electric field due to a ring at far distances on the axis?
At very large distances from the ring on its axis, the field behaves like that from a point charge:
- E ≈ (1/4πε0) × q / x2 for x >> a.
- This simplifies the analysis and is useful for distant field approximations.
11. What is the expression for electric field intensity due to a ring of radius ‘a’ and total charge ‘q’ at a point on its axis located at a distance x from its center?
The electric field intensity at an axial point of a uniformly charged ring is:
- E = (1/4πε0) × (q x) / (x2 + a2)3/2
- Where q = total charge, a = ring’s radius, x = distance from center along the axis.


































