Physics Notes for Chapter 4 Laws of Motion Class 11 - FREE PDF Download
FAQs on Laws of Motion Class 11 Physics Chapter 4 CBSE Notes - 2025-26
1. What are the core concepts covered in Class 11 Physics Chapter 4, Laws of Motion, for a quick revision?
For a quick revision of Laws of Motion, you should focus on these core concepts:
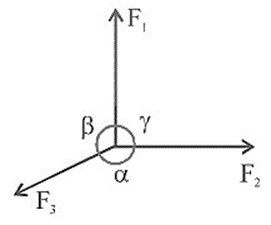
- Newton's Three Laws of Motion: The law of inertia, the relation between force and acceleration (F=ma), and the action-reaction principle.
- Momentum and Impulse: Understanding linear momentum (p=mv) and how impulse causes a change in momentum.
- Conservation of Momentum: The principle that the total momentum of an isolated system remains constant.
- Friction: The types of friction (static, kinetic, rolling) and the factors affecting them.
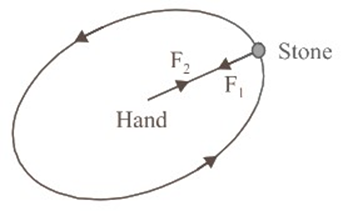
- Circular Motion: The concepts of centripetal force required for circular motion and its applications like the banking of roads.
2. How can Newton's First Law of Motion be summarized for quick revision?
Newton's First Law, also known as the Law of Inertia, can be summarized as: an object will remain at rest or in a state of uniform motion in a straight line unless acted upon by an external, unbalanced force. In essence, objects resist changes in their state of motion. The more mass an object has, the greater its inertia.
3. What is the key difference between Newton's First and Second Laws?
The key difference is that Newton's First Law is qualitative, while the Second Law is quantitative.
- The First Law defines the concept of force as something that changes an object's state of motion and introduces the concept of inertia.
- The Second Law provides a way to measure this force by relating it to the mass of the object and the acceleration it produces (F = ma). It quantifies the relationship between force, mass, and acceleration.
4. Why do Newton's Third Law action-reaction pairs never cancel each other out?
Action-reaction forces never cancel each other out because they always act on two different bodies. For forces to cancel, they must act on the same object. For example, when you push a wall (action on the wall), the wall pushes you back (reaction on you). Since one force acts on the wall and the other acts on you, they cannot cancel; instead, they produce effects on their respective objects.
5. What is the relationship between impulse and momentum as per the impulse-momentum theorem?
The impulse-momentum theorem states that the impulse applied to an object is equal to the change in its linear momentum. Impulse is the product of the force and the time duration for which it acts. This is a crucial concept for understanding collisions and short-duration forces. The relationship is summarised as I = FΔt = Δp, where Δp is the change in momentum.
6. For revision, what is the main idea behind the Law of Conservation of Linear Momentum?
The main idea is that in any isolated system (a system where no net external force acts), the total linear momentum of the system remains constant. Even if particles within the system collide or exert forces on one another, the vector sum of their momenta before the interaction is equal to the vector sum of their momenta after the interaction. This principle is fundamental in analysing collisions, explosions, and recoil.
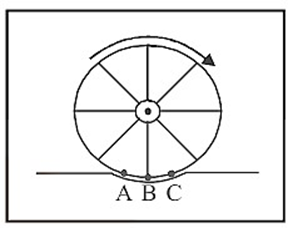
7. How do static, kinetic, and rolling friction differ from each other?
The key differences are based on the state of motion and magnitude:
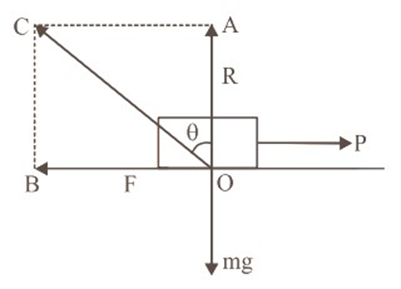
- Static Friction (fₛ): This opposing force acts when an object is at rest and prevents it from moving. Its value adjusts itself to be equal to the applied force, up to a maximum limit called limiting friction.
- Kinetic Friction (fₖ): This force acts when an object is in sliding motion. It is generally less than the maximum static friction and remains relatively constant for a given speed.
- Rolling Friction (fᵣ): This force opposes the motion when an object rolls over a surface. It is significantly smaller than both static and kinetic friction, which is why wheels are used to move heavy objects.
Generally, fᵣ < fₖ < fₛ (max).
8. Why is friction called a 'self-adjusting force'?
Friction, specifically static friction, is called a self-adjusting force because its magnitude is not fixed. When you apply a small force to an object at rest, the static friction force matches your applied force exactly, keeping the object stationary. As you increase your push, the static friction also increases to match it, up to its maximum possible value, known as limiting friction. Only when the applied force exceeds this limit does the object start to move.
9. What is the practical difference between the angle of friction and the angle of repose?
While numerically equal, they describe different physical situations:
- The Angle of Friction (θ) is defined on a horizontal surface. It is the angle between the resultant of the normal reaction and the limiting friction force, and the normal reaction itself.
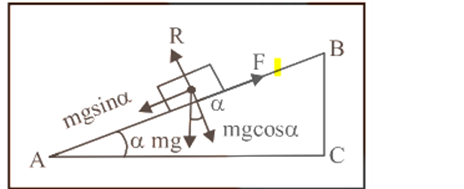
- The Angle of Repose (α) is defined for an inclined plane. It is the minimum angle of inclination of the plane with the horizontal at which a body placed on it just begins to slide down under its own weight.
For revision, remember that both are related to the coefficient of static friction by the formula μₛ = tan(θ) = tan(α).
10. What is the difference between centripetal and centrifugal force for a quick recap?
The primary difference is that centripetal force is a real force, while centrifugal force is a pseudo force (or fictitious force).
- Centripetal Force: This is the net force that acts towards the centre of a circular path, causing an object to deviate from a straight line and follow the curve. It is provided by a real source, like tension or gravity.
- Centrifugal Force: This is an apparent outward force experienced by an object in a rotating (non-inertial) frame of reference. It is not a real force but a consequence of the object's inertia.
11. Why is it safer for a cyclist to bend inwards while taking a turn?
It is safer for a cyclist to bend inwards because this action helps generate the necessary centripetal force to make the turn. By bending, a component of the normal reaction force from the ground is directed horizontally towards the centre of the curve. This provides the required centripetal force, reducing the reliance on the force of friction between the tyres and the road, which can be unreliable.
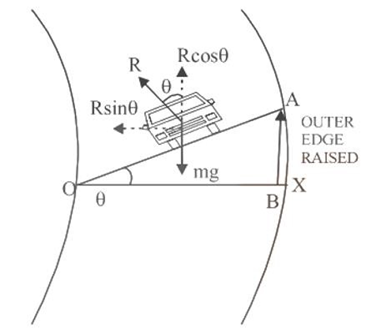
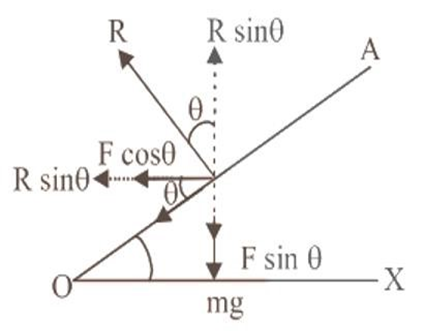
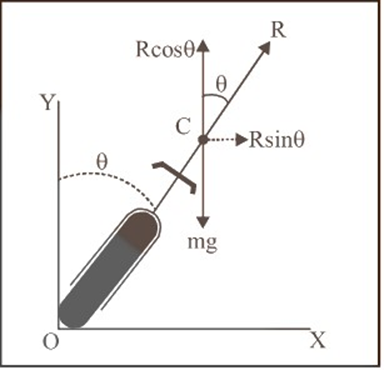
12. What is the purpose of 'banking of roads' and how does it help in turning?
The purpose of banking of roads is to provide a safer way for vehicles to take turns, especially at high speeds. By raising the outer edge of a curved road relative to the inner edge, the road surface is tilted. This inclination causes a component of the vehicle's normal reaction force to point towards the centre of the curve, supplying the necessary centripetal force. This reduces the vehicle's dependence on friction, preventing skidding and reducing wear on tyres.
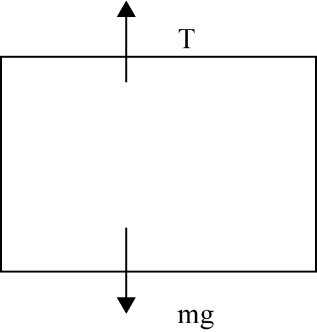
13. How does the apparent weight of a person change in a lift accelerating upwards versus downwards?
The apparent weight of a person in a lift, measured by the normal reaction (R), changes with acceleration:
- Accelerating Upwards (a): The apparent weight increases. You feel heavier because the floor pushes up with more force. The formula is R = m(g + a).
- Accelerating Downwards (a): The apparent weight decreases. You feel lighter as the floor pushes with less force. The formula is R = m(g - a).
- Moving at Constant Velocity (a=0): The apparent weight is equal to the real weight (R = mg).
- In Free Fall (a=g): The apparent weight becomes zero (R = 0), leading to a state of weightlessness.