Question

Four point charges –q, +q, +q and –q are placed on the y-axis at y=-2d, y=-d, y=+d and y=+2d respectively. The magnitude of the electric field E at a point on the x-axis at x=D, with D>>d, will behave as
$
  (a){\text{ E}} \propto \dfrac{1}{D} \\
  (b){\text{ E}} \propto \dfrac{1}{{{D^3}}} \\
  (c){\text{ E}} \propto \dfrac{1}{{{D^2}}} \\
  (d){\text{ E}} \propto \dfrac{1}{{{D^4}}} \\
$

Answer 1

Hint: In this question first plot 4 charges on y axis considering O as the origin, take a random point P on the direction of positive x-axis at a distance D from the origin, consider ${\theta _1}$be the angle that point P makes with the charge –q at positive y axis and ${\theta _2}$be the angle that point P makes with the +q change on the positive y axis. Then use the direct formula for electric fields at a point due to a point charge. Use this to find the net electric field at this point. This will help approaching the problem.


Complete step-by-step solution -



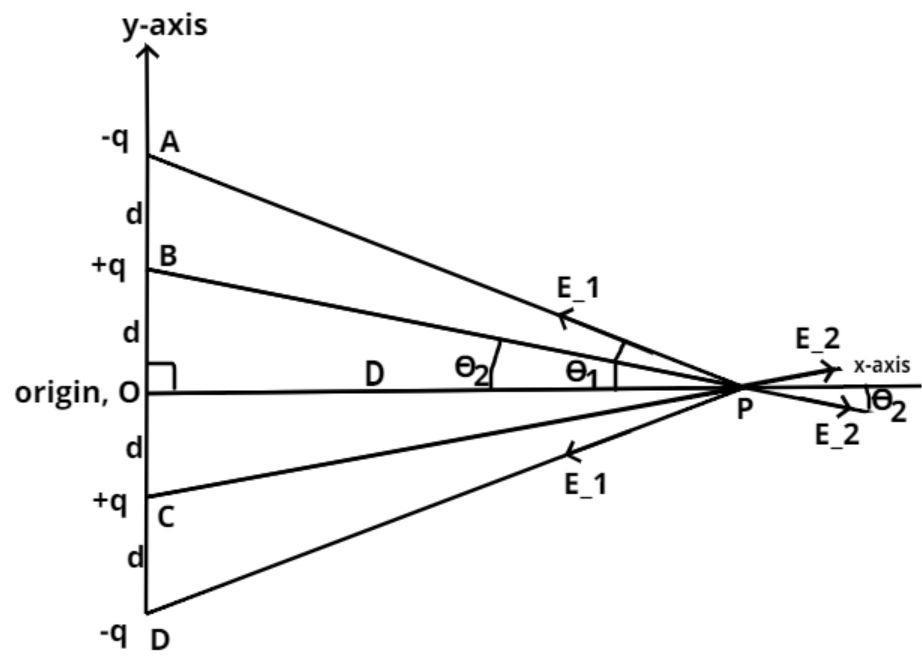
Four point charges –q, +q, +q and –q are placed on y-axis at A, B, C and D point as shown in the figure, which are at the distances, y = 2d, y = d, y = -d and y= -2d i.e. all points are at equal distance w.r.t the previous point as shown in the figure.
Now we have to find out the electric field E at a point (P) on the x-axis at X = D.
Let us suppose point P makes an angle ${\theta _1}$ with point A and D as shown in the figure.
And angle ${\theta _2}$ with point B and C as shown in the figure.
Now due to negative charge at point A and D electric field ${E_1}$ is pointed inwards as shown in the figure.
And due to positive charge at point B and C electric field ${E_2}$ is pointed outwards as shown in the figure.
Now resolve the components of electric field on the x-axis the electric field at point P is given as,
$ \Rightarrow E = 2{E_2}\cos {\theta _2} - 2{E_1}\cos {\theta _1}$.................. (1)
Now in triangle AOP apply Pythagoras theorem we have,
$ \Rightarrow {\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{perpendicular}}} \right)^2} + {\left( {{\text{base}}} \right)^2}$
$ \Rightarrow {\left( {{\text{AP}}} \right)^2} = {\left( {{\text{OA}}} \right)^2} + {\left( {{\text{OP}}} \right)^2}$
$ \Rightarrow {\left( {{\text{AP}}} \right)^2} = {\left( {{\text{2d}}} \right)^2} + {\left( D \right)^2}$
Now take square root on both sides we have,
\[ \Rightarrow \left( {{\text{AP}}} \right) = \sqrt {{{\left( {{\text{2d}}} \right)}^2} + {{\left( D \right)}^2}} \].............. (2)
Similarly
$ \Rightarrow \left( {{\text{BP}}} \right) = \sqrt {{{\left( {\text{d}} \right)}^2} + {{\left( D \right)}^2}} $.................. (3)
Now electric field at point at point P due to point charge at A is given as
$ \Rightarrow {E_1} = \dfrac{1}{{4\pi {\xi _o}}}\dfrac{{\left( q \right)}}{{{{\left( {AP} \right)}^2}}}$
Now from equation (2) we have,
$ \Rightarrow {E_1} = \dfrac{{kq}}{{{{\left( {{\text{2d}}} \right)}^2} + {{\left( D \right)}^2}}}$, where $k = \dfrac{1}{{4\pi {\xi _o}}}$
And electric field at point at point P due to point charge at B is given as
$ \Rightarrow {E_2} = \dfrac{1}{{4\pi {\xi _o}}}\dfrac{{\left( q \right)}}{{{{\left( {BP} \right)}^2}}}$
Now from equation (3) we have,
$ \Rightarrow {E_2} = \dfrac{{kq}}{{{{\left( {\text{d}} \right)}^2} + {{\left( D \right)}^2}}}$, where $k = \dfrac{1}{{4\pi {\xi _o}}}$
Now in triangle AOP cosine is the ratio of base to hypotenuse so we have,
$ \Rightarrow \cos {\theta _1} = \dfrac{{OP}}{{AP}} = \dfrac{D}{{\sqrt {{{\left( {{\text{2d}}} \right)}^2} + {{\left( D \right)}^2}} }}$
Similarly in triangle BOP
$ \Rightarrow \cos {\theta _2} = \dfrac{{OP}}{{BP}} = \dfrac{D}{{\sqrt {{{\left( {\text{d}} \right)}^2} + {{\left( D \right)}^2}} }}$
Now from equation (1) we have,
$ \Rightarrow E = 2\dfrac{{kq}}{{{{\left( {\text{d}} \right)}^2} + {{\left( D \right)}^2}}}\dfrac{D}{{\sqrt {{{\left( {\text{d}} \right)}^2} + {{\left( D \right)}^2}} }} - 2\dfrac{{kq}}{{{{\left( {{\text{2d}}} \right)}^2} + {{\left( D \right)}^2}}}\dfrac{D}{{\sqrt {{{\left( {{\text{2d}}} \right)}^2} + {{\left( D \right)}^2}} }}$
Now simplify this we have,
\[ \Rightarrow E = \dfrac{{2kqD}}{{{{\left[ {{{\left( {\text{d}} \right)}^2} + {{\left( D \right)}^2}} \right]}^{\dfrac{3}{2}}}}} - \dfrac{{2kqD}}{{{{\left[ {{{\left( {{\text{2d}}} \right)}^2} + {{\left( D \right)}^2}} \right]}^{\dfrac{3}{2}}}}}\]
Now take ${D^2}$ common from the denominator we have,
\[ \Rightarrow E = \dfrac{1}{{{{\left( {{D^2}} \right)}^{\dfrac{3}{2}}}}}\left\{ {\dfrac{{2kqD}}{{{{\left[ {1 + {{\left( {\dfrac{d}{D}} \right)}^2}} \right]}^{\dfrac{3}{2}}}}} - \dfrac{{2kqD}}{{{{\left[ {1 + {{\left( {\dfrac{{2d}}{D}} \right)}^2}} \right]}^{\dfrac{3}{2}}}}}} \right\}\]
\[ \Rightarrow E = \dfrac{{2kq}}{{{D^2}}}\left\{ {{{\left[ {1 + {{\left( {\dfrac{d}{D}} \right)}^2}} \right]}^{ - \dfrac{3}{2}}} - {{\left[ {1 + 4{{\left( {\dfrac{d}{D}} \right)}^2}} \right]}^{ - \dfrac{3}{2}}}} \right\}\]
Now according to binomial expansion approximation (we use this approximation because it is given that D>>>d,$\dfrac{d}{D} < < 1 \Rightarrow \dfrac{{{d^2}}}{{{D^2}}} < < < 1 \Rightarrow \dfrac{{{d^3}}}{{{D^3}}} \simeq 0$ and so on, so higher terms are neglected) which is given as ${\left( {1 + x} \right)^{ - n}} = 1 - nx$ so use this property in above equation we have,
\[ \Rightarrow E = \dfrac{{2kq}}{{{D^2}}}\left\{ {\left[ {1 - \dfrac{3}{2}\dfrac{{{d^2}}}{{{D^2}}}} \right] - \left[ {1 - 4 \times \dfrac{3}{2}\dfrac{{{d^2}}}{{{D^2}}}} \right]} \right\}\]
Now simplify this we have,
\[ \Rightarrow E = \dfrac{{2kq}}{{{D^2}}}\left\{ {1 - \dfrac{3}{2}\dfrac{{{d^2}}}{{{D^2}}} - 1 + 6\dfrac{{{d^2}}}{{{D^2}}}} \right\}\]
\[ \Rightarrow E = \dfrac{{2kq}}{{{D^2}}}\left\{ { - \dfrac{3}{2}\dfrac{{{d^2}}}{{{D^2}}} + 6\dfrac{{{d^2}}}{{{D^2}}}} \right\} = \dfrac{{2kq}}{{{D^2}}}\left[ {\dfrac{{9{d^2}}}{{2{D^2}}}} \right] = \dfrac{{9kq{d^2}}}{{{D^4}}}\]
So as we see that the electric field at point P is behaves as,
$ \Rightarrow E \propto \dfrac{1}{{{D^4}}}$
So this is the required answer.
Hence option (D) is the correct answer.

Note – Electric field is considered as a region around a charged particle in which when another particle is placed than this particle experiences a force. The electric field intensity is simply the strength of the force that is being experienced by this placed object within the region of one charged particle. The electric field is composed of electric lines of forces depicting the region of electric field. For a positive charge these are generally radially outwards and for a negative charge these are radially inwards.