Question

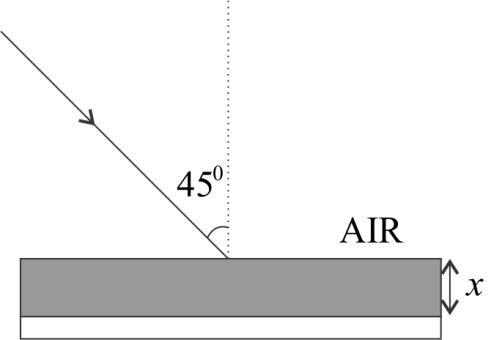
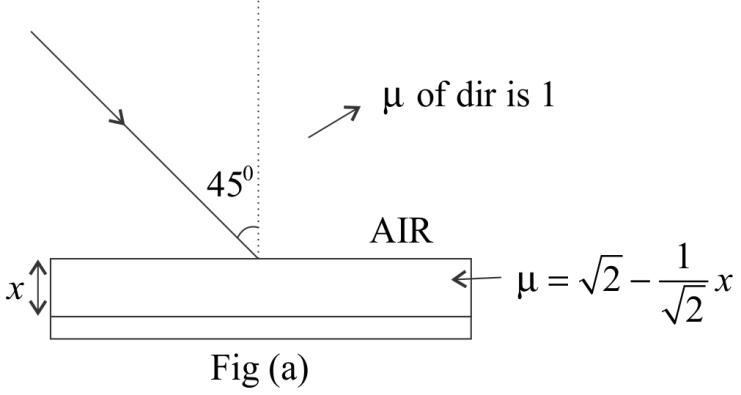
A ray of light into a transparent liquid from as shown in Fig. The Refractive Index of the liquid varies with depth $x$ from the topmost surface as $\mu = \sqrt {2 - } \dfrac{1}{{\sqrt 2 }}x$ where $x$ is in meter. The depth of the liquid medium is sufficiently large. The maximum depth reached by the ray inside the liquid will be:

Answer 1

Hint: As the rays are going from lighter medium to denser medium it bends towards normal, as the refractive is changing continuously with the distance, and it is decreases when the rays are traveling down the slab the ray will refract at ${90^ \circ }$ at Critical angle. Hence by using Snell’s law we can calculate the maximum depth.

Formula Used:
Snell’s law
${\mu _1}\sin {\theta _1} = {\mu _2}\sin {\theta _2}$
${\mu _1}$ is the refractive index of incident ray
${\theta _1}$ is the angle of incident
${\mu _2}$ is the refractive index of refracted rays,
${\theta _2}$ is the angle of refraction.

Complete step by step answer:
Here, the angle of incident is given i.e.
${\theta _1} = {45^ \circ }$
And refractive index of water decreases continuously & ${\mu _2} = \sqrt 2 - \dfrac{1}{{\sqrt 2 }}x$
By Figure, we can say that

And as we know the surrounding medium is Air.
${\mu _{(Air)}} = 1$
By Applying Snell’s law, we can solve it.
When the ray travels from top to bottom of the slab, the refractive Index of the slab decreases as ${\mu _2} = \sqrt 2 - \dfrac{1}{{\sqrt 2 }}x$ and at last the will refract at ${90^ \circ }$ at Critical angle, so angle of refraction will become ${\mu _i} = {90^ \circ }$.
So, by applying Snell’s law, we get
${\mu _1} \times \sin 45 = \mu (x) \times \sin 90$
$1 \times \dfrac{1}{{\sqrt 2 }} = \left( {\sqrt 2 - \dfrac{1}{{\sqrt 2 }}x} \right) \times 1$ $[\because {\mu _1}$ = $1 \& \mu \left( x \right) = \sqrt 2 - \dfrac{1}{{\sqrt 2 }}x$ & $\sin {90^o} = 1]$
$\dfrac{1}{{\sqrt 2 }} - \dfrac{{\sqrt 2 }}{1} = - \dfrac{1}{{\sqrt 2 }}x$
$\dfrac{{1 - 2}}{{\sqrt 2 }} = - \dfrac{1}{{\sqrt 2 }}x$ or $ - \dfrac{1}{{\sqrt 2 }} = - \dfrac{1}{{\sqrt 2 }}x$
So, $x = 1$

Hence, the maximum depth of the slab is $1 meter$.

Additional Information:
Snell’s law:
Snell’s law (also called Snell-Descartes law and law of refraction) is a formula used to describe the relationship between the angle of incident and refraction, when referring to light or other waves passing through a boundary between two different isotropic media, such as water, glass or air.
Snell’s law states that the ratio of the sines of the angles of incidence and refraction is equivalent to the ratio of phase of velocities in the two media, or equivalent to the reciprocal of the ratio of the indices of refraction.
$\dfrac{{\sin {\theta _2}}}{{\sin {\theta _1}}} = \dfrac{{{V_2}}}{{{V_1}}} = \dfrac{{{n_1}}}{{{n_2}}}$
Each $\theta $ is measured with the normal of the boundary.

Note: As the Rays are passing from air (lighter ) to liquid (denser) it will bends towards the normal as the refractive index of $x$ & is decreases towards downward direction, So, at light it will come out at ${90^ \circ }$. So, the angle of refraction is ${90^ \circ }$, by Applying Snell’s we can calculate the distance $x$.