Question

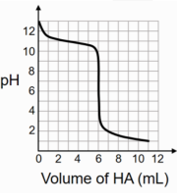
A 0.1 M weak base (B) solution is titrated with 0.1 M of a strong acid (HA). The image below depicts the change in pH of the solution as a function of the amount of HA added. What is the \[p{k_b}\] of the base? The neutralisation reaction is given by \[B + HA - \]\[B{H^ + } + {A^ - }\].

Answer 1

Hint: In general, titration is a type of quantitative analysis that involves measuring the volume of a chemical species' solution in a suitable solvent in order to estimate its quantity. The Law of Equivalence underpins this strategy. As a result, titration can be defined as the process of calculating the volume of reagents by bringing a specific reaction to a close. The titrant is the solution used in titration that has an accurate concentration and the titrated substance is the substance whose volume needs to be determined.

Complete Step by Step Solution:
The given chemical reaction is \[B + HA \to B{H^ + } + {A^ - }\]

Conditions	B (0.1 M)	HA (0.1 M)	pH
At V = 0 ml		0 ml	13
At V = 3 ml		3 ml → 50% neutralisation	11
At V = 6 ml		6 ml → Equivalence Point	3 to 9

At Equivalence Point:

B	HA	BH+	A-
$0.1 \times 6$ = 0.6 mmol	$0.1 \times 6$ = 0.6 mmol
0	0	0.6 mmol

Total vol. = 12 ml
Concentration of salt = \[\dfrac{{0.6}}{{12}}\]
pH = 6 = \[\sqrt {\dfrac{{{k_w}}}{{{k_b}}}} \times c = \sqrt {\dfrac{{{{10}^{ - 14}} \times 0.6}}{{{k_b} \times 12}}} \]
{ pH = 0.6, \[[{H^ + }] = {10^{ - 6}}\]}
\[ \Rightarrow \]pH = 0.6 = \[\sqrt {\dfrac{{{k_w}}}{{{k_b}}} \times \dfrac{{0.1 \times 6}}{{12}}} \]
\[{10^{ - 12}} = \dfrac{{{{10}^{ - 14}} \times {{10}^{ - 1}}}}{{{k_b}}} \times \dfrac{1}{2}\]
$ \Rightarrow {k_b} = 5 \times {10^{ - 4}} \\$
$ \Rightarrow p{k_b} = - \log {k_b} = - \log (5 \times {10^{ - 4}}) = - \log 5 + 4\log 10 \\$
$ \Rightarrow p{k_b} = 4 - 0.7 \\$
$ \Rightarrow p{k_b} = 3.3 \\ $

Note: \[p{k_b}\] is the symbol which is used to estimate the alkalinity of the molecule. It is used to determine the base's strength. The lesser the \[p{k_b}\] value, the more potential the base will be having to dilute an acid. It is equivalent to the negative of logarithm of the base dissociation constant i.e. \[{k_b}\].
\[p{k_b} = - \log {k_b}\]; \[{k_b}\] or base dissociation constant is the symbol used to estimate a base’s strength. It indicates the amount of dissociation of a base in an aqueous solution. \[{k_b}\] is used to distinguish a strong base from a weaker one. More the value of \[{k_b}\] more would be its dissociation.