




How Does Entropy Vary in Reversible and Irreversible Processes?
Entropy is a fundamental thermodynamic property used to quantify the degree of randomness or molecular disorder in a system. Its behaviour during various thermodynamic processes is crucial for understanding the second law of thermodynamics, predicting spontaneity, and solving problems in JEE Main and Advanced examinations.
Definition and Meaning of Entropy
Entropy, denoted by $S$, is defined as a state function that measures the degree of disorder or randomness in a thermodynamic system. It describes how energy in a system becomes more uniformly spread out at a given temperature.
In statistical terms, entropy measures the number of microscopic arrangements (microstates) corresponding to a macroscopic state. For chemical and physical processes, entropy is central to predicting the direction of change. Further conceptual details are discussed in Thermodynamics Overview.
Entropy Change and Its Mathematical Expression
The change in entropy $(\Delta S)$ for a reversible process is defined by the equation:
$\Delta S = \dfrac{q_\text{rev}}{T}$
Here, $q_\text{rev}$ is the heat transfer during a reversible process, and $T$ is the absolute temperature in Kelvin. The SI unit of entropy is joules per kelvin (J/K).
Entropy Changes in Different Thermodynamic Processes
Entropy change varies with the type of thermodynamic process. The detailed expressions for entropy change in principal processes are given below.
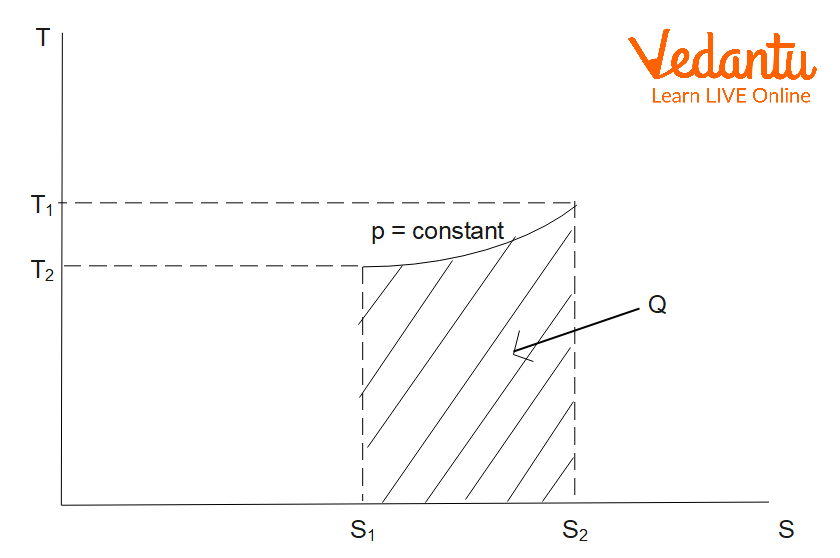
Entropy Change in Isobaric Process
An isobaric process occurs at constant pressure. For an ideal gas heated from temperature $T_1$ to $T_2$ at constant pressure:
$\Delta S_\text{isobaric} = m\,C_p \ln \left(\dfrac{T_2}{T_1}\right)$
Here, $m$ is the mass, and $C_p$ is the specific heat at constant pressure. Entropy increases as temperature increases under constant pressure conditions.
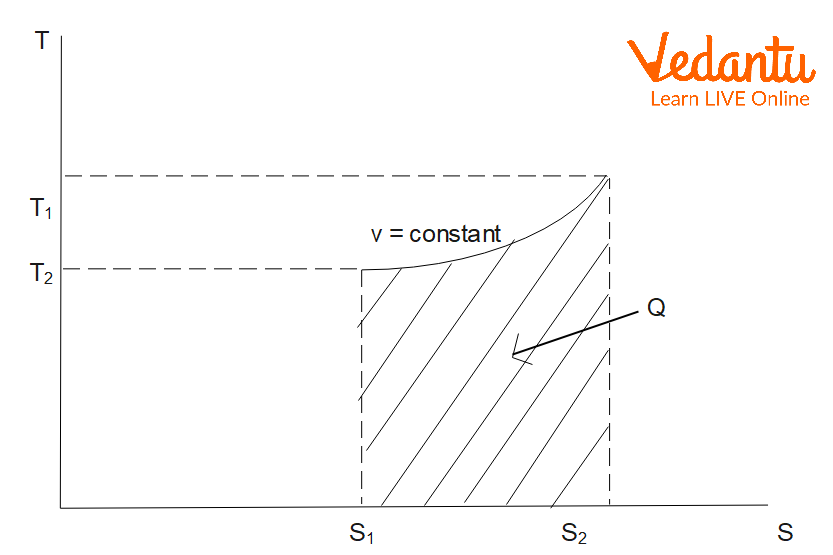
Entropy Change in Isochoric Process
An isochoric process takes place at constant volume. For an ideal gas with temperature increasing from $T_1$ to $T_2$ at constant volume:
$\Delta S_\text{isochoric} = m\,C_v \ln \left(\dfrac{T_2}{T_1}\right)$
Here, $C_v$ is the specific heat at constant volume. Entropy also increases with temperature at constant volume.
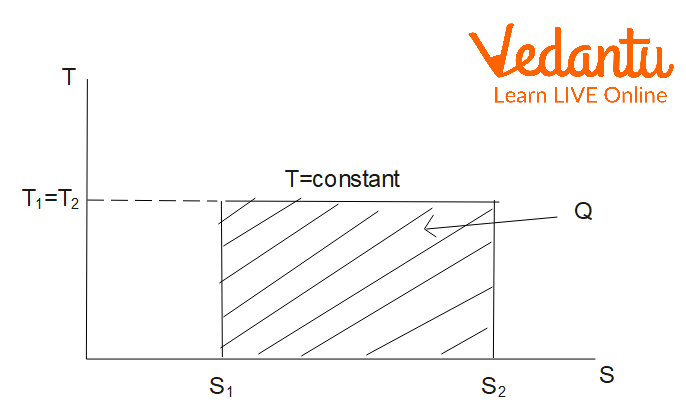
Entropy Change in Isothermal Process
An isothermal process occurs at constant temperature. For one mole of an ideal gas undergoing expansion or compression from volume $V_1$ to $V_2$ at temperature $T$:
$\Delta S_\text{isothermal} = nR \ln \left(\dfrac{V_2}{V_1}\right)$
Alternatively, using the ideal gas equation, this can be written as $\Delta S = nR \ln \left(\dfrac{P_1}{P_2}\right)$. Entropy increases during isothermal expansion.
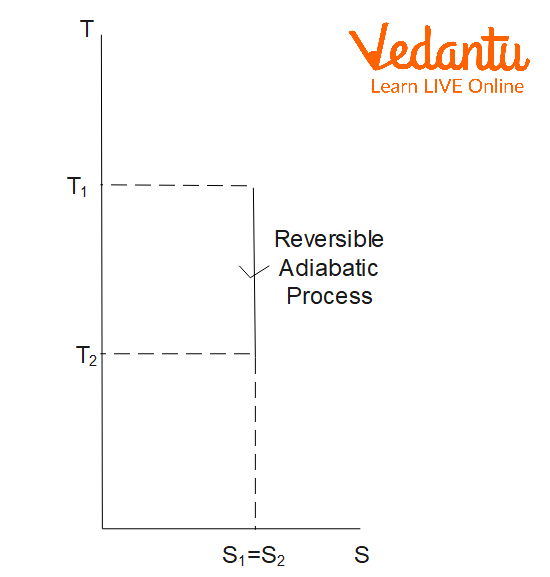
Entropy Change in Adiabatic Process
In an adiabatic process, no heat is exchanged with the surroundings ($q=0$). For a reversible adiabatic process:
$\Delta S_\text{adiabatic,\,rev} = 0$
There is no change in the entropy of the system since the process occurs without heat transfer.
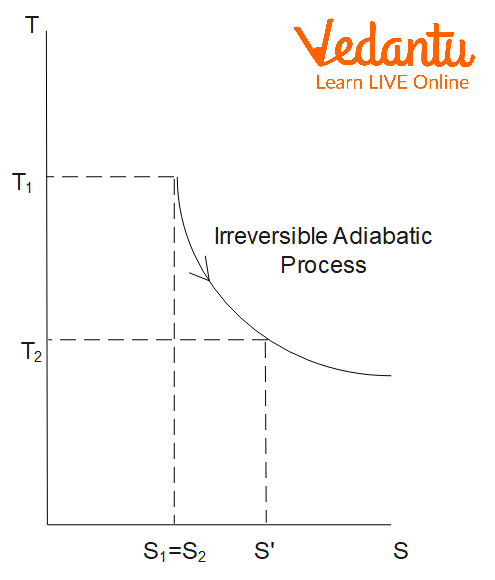
Entropy in Irreversible Processes
For an irreversible process, the total entropy of the universe (system plus surroundings) always increases. The mathematical expression is:
$\Delta S_\text{irreversible} \geq \dfrac{q}{T}$
In irreversible adiabatic processes, although $q=0$ for the system, entropy increases due to dissipative effects such as friction or non-equilibrium changes.
Entropy in Quasi-Static Processes
A quasi-static process occurs infinitely slowly, allowing the system to remain nearly in equilibrium throughout. Entropy change follows:
$dS = \dfrac{dQ}{T} + I$
Here, $I$ represents irreversible entropy generation, which is zero for purely reversible (quasi-static) steps but positive if any irreversibility is involved.
The relationship between various processes and entropy change facilitates understanding the fundamental laws governing energy transformations. Connections to energy transfer mechanisms are discussed in First Law of Thermodynamics.
Summary Table: Entropy Change in Major Processes
| Process | Entropy Change ($\Delta S$) |
|---|---|
| Isobaric | $m\,C_p \ln \left(\dfrac{T_2}{T_1}\right)$ |
| Isochoric | $m\,C_v \ln \left(\dfrac{T_2}{T_1}\right)$ |
| Isothermal | $nR \ln \left(\dfrac{V_2}{V_1}\right)$ |
| Adiabatic (Reversible) | $0$ |
| Adiabatic (Irreversible) | $>0$ |
Physical Examples of Entropy Change
Entropy changes occur in diverse physical situations, such as heating solids and liquids, phase transitions, and mixing substances. Everyday examples include the melting of ice, diffusion of gases, and thermal conduction.
For instance, the entropy increases when a solid melts or when a solute dissolves in a solvent due to an increase in disorder. More on energy transfer can be found in Understanding Heat Pumps.
Key Properties of Entropy
- State function, independent of path
- Extensive property, depends on system size
- SI unit is joule per kelvin (J/K)
- Entropy increases with temperature
- In isolated system, entropy does not decrease
- Symbol is $S$, while $S^\circ$ represents standard entropy
The properties and calculations of entropy are often used to predict spontaneity and equilibrium in thermodynamic systems and can be useful for understanding entropy of discrete random variables and distributions.
Conclusion on Entropy of Different Processes
Entropy serves as a crucial parameter to assess the direction and feasibility of thermodynamic transformations. In all natural processes, total entropy increases or remains constant, but never decreases for an isolated system. The study of entropy across different processes aids significantly in mastering concepts essential for thermodynamics topics in JEE examinations.
Further insights into work and entropy transformations can be explored in Compression Work Explained.
FAQs on Understanding Entropy Changes in Different Processes
1. What is entropy in thermodynamics?
Entropy in thermodynamics is a measure of disorder or randomness in a system. It reflects how energy is distributed within a system and is fundamental to the second law of thermodynamics.
Key points:
- Higher entropy indicates higher disorder.
- It is represented by the symbol S.
- Entropy tends to increase in spontaneous processes.
- It is measured in Joules per Kelvin (J/K).
2. Describe the change in entropy during an irreversible process.
During an irreversible process, the entropy of the universe increases. This increase in entropy distinguishes irreversible processes from reversible ones.
- There is a net positive change in total entropy.
- The process cannot be reversed without external intervention.
- Examples include natural phenomena like mixing, spontaneous heat flow, and chemical reactions.
3. How does entropy change in a reversible process?
In a reversible process, the total entropy change of the system and surroundings is zero.
- The process can be reversed without leaving any net change in the system and surroundings.
- All steps occur infinitely slowly in equilibrium.
- ΔS (change in entropy) of the universe is zero.
4. What are the main differences between reversible and irreversible processes in terms of entropy?
The primary difference between reversible and irreversible processes revolves around entropy change.
- Reversible process: Entropy change of universe = 0.
- Irreversible process: Entropy change of universe > 0.
- Irreversible processes are natural and spontaneous; reversible processes are theoretical and ideal.
5. What is the entropy change when heat is transferred to a system at constant temperature?
When heat (q) is transferred to a system at constant temperature (T), the change in entropy (ΔS) is given by:
- ΔS = q/T
- Applicable only in reversible processes.
- q must be in Joules, and T in Kelvin.
6. How does entropy change during the free expansion of an ideal gas?
During the free expansion of an ideal gas, entropy increases due to increased randomness.
- No work is done and no heat is exchanged with surroundings.
- The process is irreversible.
- The system becomes more disordered as molecules occupy a larger volume.
7. Explain entropy change during phase transitions such as melting and boiling.
Entropy increases during phase transitions because the system becomes more disordered.
- Melting (solid to liquid): Entropy increases as molecules move more freely.
- Boiling (liquid to gas): Entropy increases significantly due to greater molecular motion.
- These transitions occur at constant temperature and pressure.
8. Why is entropy considered a state function?
Entropy is a state function because its value depends only on the initial and final states of the system, not on the process used to get there.
- Path-independent.
- Can be calculated using any reversible path between states.
- Supported by the second law of thermodynamics.
9. What is the significance of entropy in the second law of thermodynamics?
The second law of thermodynamics states that the total entropy of the universe always increases for a spontaneous process.
- Explains direction of natural processes.
- Helps predict feasibility of reactions and processes.
- Entropy increase is a measure of irreversible energy dispersal.
10. How can entropy change be calculated for an isothermal expansion of an ideal gas?
For an isothermal expansion of an ideal gas, the entropy change (ΔS) can be calculated using:
- ΔS = nR ln(V₂/V₁)
- n = number of moles, R = gas constant.
- V₁ and V₂ are initial and final volumes, respectively.
- This formula applies only under isothermal, reversible conditions.
11. State the mathematical expression for entropy change in a reversible process.
The entropy change for a reversible process is calculated as:
- ΔS = qrev/T
- Here, qrev is the reversible heat exchange and T is temperature in Kelvin.
- Applicable only for reversible transitions.
12. Does entropy always increase in all chemical reactions?
Entropy does not always increase in all chemical reactions, but for the universe, entropy never decreases.
- For spontaneous reactions, total entropy increases.
- For some reactions, system entropy may decrease, but surroundings' entropy increases more.


































