




Step-by-Step Method for Vector Subtraction with Practical Examples
The subtraction of vectors is the operation that, given two vectors of the same kind, produces a third vector representing their difference, defined through addition with the negative of the second vector.
Definition and Notation of Vector Subtraction
Definition: If $\vec{a}$ and $\vec{b}$ are vectors of the same physical quantity, their difference is denoted as $\vec{a} - \vec{b}$ and defined by $\vec{a} - \vec{b} = \vec{a} + (-\vec{b})$, where $-\vec{b}$ is the additive inverse of $\vec{b}$, possessing identical magnitude and opposite direction.
Geometric Interpretation Using the Parallelogram Law
To subtract $\vec{b}$ from $\vec{a}$ by the parallelogram law, represent both vectors from a common initial point. The vector $-\vec{b}$ is constructed by reversing the direction of $\vec{b}$, and the resultant $\vec{a} + (-\vec{b})$ forms the diagonal of the parallelogram built on $\vec{a}$ and $-\vec{b}$ sharing the same origin.
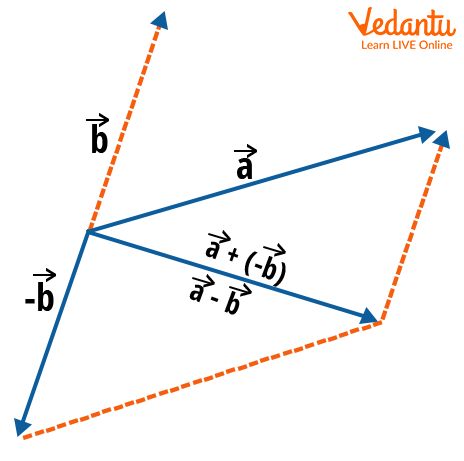
Graphical Construction via the Triangle Law
According to the triangle law, place $\vec{b}$ and $-\vec{b}$ tail-to-tail. Draw $\vec{a}$ from the same origin as $\vec{b}$; the vector from the tip of $\vec{b}$ to the tip of $\vec{a}$ (with both vectors coinitial) represents $\vec{a} - \vec{b}$.
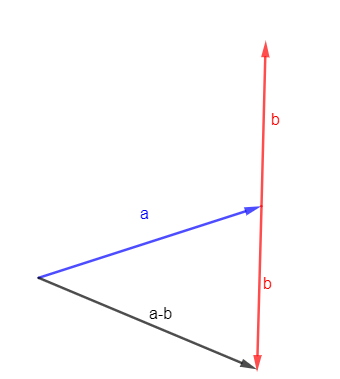
Componentwise Formula for Vector Subtraction
If $\vec{a} = \langle a_1, a_2, a_3 \rangle$ and $\vec{b} = \langle b_1, b_2, b_3 \rangle$, then $\vec{a} - \vec{b} = \langle a_1-b_1, a_2-b_2, a_3-b_3 \rangle$. Each component is subtracted independently, which is a direct result of the definition of vector addition and scalar multiplication.
Essential Properties of the Subtraction Operation
The following conceptual points should be noted regarding vector subtraction:
- Only defined between vectors of identical physical type
- Not commutative; $\vec{a} - \vec{b} \neq \vec{b} - \vec{a}$ in general
- Not associative; $(\vec{a} - \vec{b}) - \vec{c} \neq \vec{a} - (\vec{b} - \vec{c})$
- $\vec{a} - \vec{a} = \vec{0}$ always holds
- Magnitude depends on the angle and moduli
For a detailed study of related ideas, refer to Addition Of Vectors and Vector Algebra.
Magnitude of the Difference Vector and Algebraic Relations
The square of the magnitude of $\vec{a} - \vec{b}$ follows from the law of cosines and properties of the dot product: $\|\vec{a} - \vec{b}\|^2 = \|\vec{a}\|^2 + \|\vec{b}\|^2 - 2\,\vec{a} \cdot \vec{b}$. This result is essential for quantitative questions involving the angle between vectors.
Illustrative Calculations Involving Vector Subtraction
Example: Given $\vec{a} = \langle 4, -2, 3 \rangle$, $\vec{b} = \langle 1, -2, 5 \rangle$, compute $\vec{a} - \vec{b}$.
Subtract components: $4-1=3$, $-2-(-2)=0$, $3-5=-2$. Thus, $\vec{a} - \vec{b} = \langle 3, 0, -2 \rangle$.
Example: For $\vec{a} = \langle 3, 5 \rangle$, $\vec{b} = \langle 2, 6 \rangle$, evaluate $\vec{a} - \vec{b}$.
Compute: $3-2=1$, $5-6=-1$. The result is $\langle 1, -1 \rangle$.
Example: If $\vec{a}$ and $\vec{b}$ are unit vectors with angle $\theta$ between them, determine $\|\vec{a} - \vec{b}\|$ in terms of $\theta$.
$\|\vec{a} - \vec{b}\|^2 = 1 + 1 - 2\cos\theta = 2(1-\cos\theta) = 4\sin^2\left(\dfrac{\theta}{2}\right)$, so $\|\vec{a} - \vec{b}\| = 2\sin \left(\dfrac{\theta}{2}\right)$.
Example: If $\|\vec{a} + \vec{b}\| = \|\vec{a} - \vec{b}\|$, prove the vectors are orthogonal.
Square both sides: $\|\vec{a} + \vec{b}\|^2 = \|\vec{a} - \vec{b}\|^2$. So $2\vec{a} \cdot \vec{b} = -2\vec{a} \cdot \vec{b}$, implying $\vec{a} \cdot \vec{b} = 0$. Therefore, $\vec{a}$ and $\vec{b}$ are perpendicular.
Frequent Misconceptions in Vector Subtraction
Common Error: Attempting to subtract a scalar from a vector or subtract vectors of different types is undefined; subtraction applies only to vectors of the same physical nature and dimensionality.
For further operations on vectors, see Scalar Product Of Vectors and Vector Triple Product for related algebraic structure.
Componentwise subtraction, geometric visualization, and the non-commutative character of subtraction constitute essential points for problem-solving in vector algebra and System Of Linear Equations contexts.
FAQs on How to Subtract Vectors: A Simple Student Guide
1. What is the subtraction of vectors?
Subtraction of vectors is a process where one vector is removed from another by adding its negative, resulting in a new vector.
- The negative of a vector B is a vector with the same magnitude as B but in the opposite direction.
- The subtraction A - B is performed by adding vector A and the negative of vector B, written as A + (-B).
- This method uses the triangle law of vector addition.
2. How do you subtract two vectors geometrically?
Vectors are subtracted geometrically by connecting their initial and terminal points using the triangle or parallelogram method.
- Reverse the direction of the vector being subtracted (find its negative).
- Place the tail of the negative vector at the head of the first vector.
- Draw the resultant from the tail of the first vector to the head of the negative vector.
3. What is the formula for subtraction of vectors?
The formula for subtraction of vectors involves adding the negative of the second vector to the first:
- A - B = A + (-B)
- Here, -B means a vector equal in magnitude to B but opposite in direction.
4. What is the graphical representation of vector subtraction?
Graphically, vector subtraction is shown by arranging the two vectors head-to-tail and drawing the resultant.
- Draw vector A.
- At the tip of A, draw vector -B.
- The resultant vector (A - B) is drawn from the tail of A to the tip of -B.
5. How is vector subtraction different from scalar subtraction?
Vector subtraction considers both magnitude and direction, while scalar subtraction only considers magnitude.
- In vector subtraction, the direction of the vectors matters.
- Resultant vector may point in a different direction based on the input vectors.
- In scalar subtraction, you simply subtract numbers without direction.
6. Can you subtract vectors with different magnitudes and directions?
Yes, vectors of any magnitude and direction can be subtracted using graphical or analytical methods.
- Use the component method for vectors with different directions.
- Convert both vectors into components, subtract each corresponding component.
7. What is the algebraic method for subtracting vectors?
The algebraic method of vector subtraction uses components:
- If A = (Ax, Ay) and B = (Bx, By),
- Then A - B = (Ax - Bx, Ay - By)
8. Why is subtracting one vector from another important in physics?
Subtracting vectors helps calculate differences like displacement, velocity change, or force direction.
- Finds net displacement (difference between starting and ending points).
- Determines resultant velocities or forces.
- Is essential for solving many real-life physics problems.
9. How do you find the magnitude of the difference between two vectors?
To find the magnitude of the difference between two vectors:
- Subtract their respective components: (A−B).
- Apply the Pythagorean theorem if in two dimensions: |A - B| = √[(Ax-Bx)2 + (Ay-By)2].
10. Explain the triangle law of vector subtraction with an example.
The triangle law states that when two vectors are arranged head to tail, the closing side represents their sum or difference.
- To subtract vector B from vector A, draw A and then -B starting from A's head.
- The vector from the tail of A to the head of -B is A - B.
- Example: If A = 5 units east, B = 3 units north, draw A right and -B downward; join the start to the end for the resultant.
11. Is vector subtraction commutative or associative?
Vector subtraction is neither commutative nor associative.
- Commutative: A - B ≠ B - A
- Associative: (A - B) - C ≠ A - (B - C)
12. What is the physical meaning of A − B in vectors?
A − B represents the vector difference, or the change from B to A.
- It shows how much and in what direction you must move to go from B to A.
- Useful in finding relative displacement or change in velocity.
























