Understanding Pulley and Constraint Relations in Physics

A pulley imposes a mechanical constraint on the connected bodies, mathematically relating their displacements, velocities, and accelerations through the inextensibility of the string and the characteristics of the pulley system.

Formal Constraint Equation in Ideal Pulley Systems

In any ideal pulley configuration, the total length of the inextensible string remains constant. For two bodies $A$ and $B$ attached by a light, inextensible string over a frictionless, massless pulley, let $x_A$ and $x_B$ denote their respective positions relative to a fixed reference. The constraint is expressed as

$x_A + x_B = \text{constant}$

Differentiating with respect to time yields the velocity constraint:

$v_A + v_B = 0$

A further differentiation gives the acceleration relation:

$a_A + a_B = 0$

This formalizes the fundamental link between linear kinematics of the connected bodies in simple pulley systems.

Mathematical Formulation of Pulley Constraint Relations

For a system involving multiple pulleys and strings, the general constraint is obtained by accounting for all movable blocks and fixed supports. For a massless, frictionless pulley, let $l$ be the total length of the string, which remains unchanged:

$l = f(x_1, x_2, ..., x_n)$

where $x_i$ are positions of the masses and pulleys. Each segment is measured from a fixed support to a block or pulley as appropriate. This leads to a linear relation among displacements, and hence among velocities and accelerations.

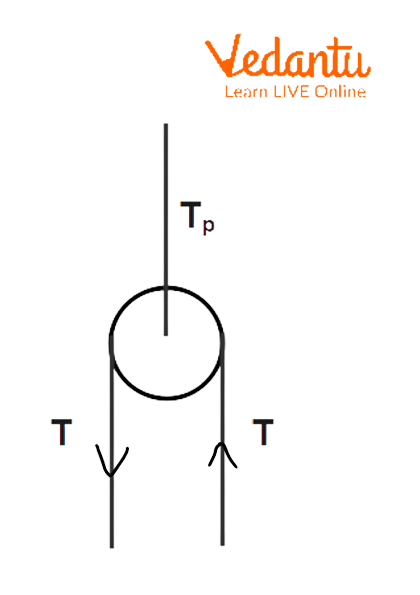
Tension Distribution in Massless Pulley Arrangements

In an ideal (massless, frictionless) pulley, the tension is the same throughout a continuous segment of the string. At a massless movable pulley supporting two symmetrical segments with tension $T$, the upward force is $2T$. If the supported mass is $m$, then at equilibrium:

$2T = m g$

Thus, the tension in each segment is $T = \frac{m g}{2}$. This result is central to analyzing Atwood's machine and other compound pulley systems.

For further exploration, see Pulley And Constraint Relations.

General Expression for Power Delivered by Tension Forces

The mechanical constraint implies that the vector sum of the power delivered by all string tensions is zero for an ideal system:

$\sum_i \vec{T}_i \cdot \vec{v}_i = 0$

On differentiating, the analogous result for accelerations is:

$\sum_i \vec{T}_i \cdot \vec{a}_i = 0$

These relations are universal for all configurations of ideal pulleys and strings.

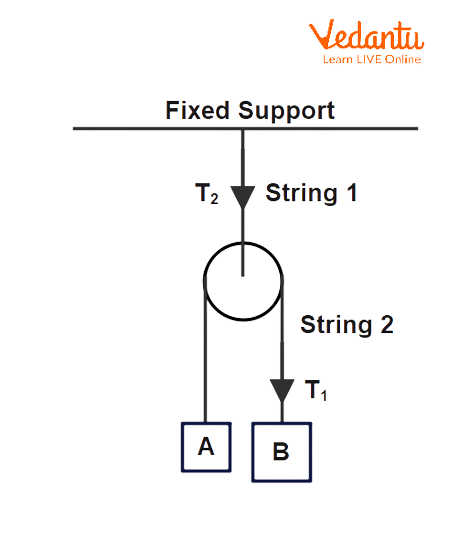
Constraint Analysis in Compound Pulley Systems

For systems involving movable pulleys, write the string-length constraint by examining the dependence of each string segment on the relevant blocks and pulleys. For example, if mass $A$ is suspended from a movable pulley and the ends of the string are attached to fixed supports, the total length equation is

$2 x_A + x_B = \text{constant}$

Here, $x_A$ is the displacement of the movable pulley (and attached body) and $x_B$ is the displacement of a second mass at the free end. Differentiation gives the velocity and acceleration relations:

$2 v_A + v_B = 0$

$2 a_A + a_B = 0$

Solved Problem: Acceleration and Tension in Two-Block Pulley System

Example. Consider two masses $m_1 = 7\,\mathrm{kg}$ and $m_2 = 9\,\mathrm{kg}$ suspended from either side of a light, frictionless pulley. Find the acceleration of the blocks and the tension in the string.

Solution.

Let $T$ be the tension, $a$ the magnitude of acceleration (down for $m_2$, up for $m_1$ by the constraint $a_1 + a_2 = 0$). Apply Newton’s second law to each block:

$T - m_1 g = m_1 a$

$m_2 g - T = m_2 a$

Add the equations:

$m_2 g - m_1 g = (m_1 + m_2)a$

Substitute $m_1 = 7$ kg, $m_2 = 9$ kg, $g = 10$ m/s$^2$ for calculation:

$a = \dfrac{(9 - 7)\times 10}{7 + 9} = \dfrac{20}{16} = 1.25\,\mathrm{m/s^2}$

Now, $T = m_1 g + m_1 a = 7 \times 10 + 7 \times 1.25 = 70 + 8.75 = 78.75\,\mathrm{N}$.

A comprehensive study of pulleys also covers tension computation, frictional corrections, and energy methods—refer to Forces On Pulleys 404 for advanced cases.

Common Pulley Systems in JEE Main Problems

• Simple Atwood machine
• Movable pulley doubling tension
• Multiple connected pulleys
• Two blocks with single/multiple pulleys
• Pulleys with fixed and movable supports
• Inclined plane systems with pulleys

Constraint Misconceptions and Exam Cautions

A frequent error is to overlook the impact of movable pulleys on the kinematic constraints. Always identify whether a pulley is fixed or movable, and count each segment of string separately when writing the constraint equation.

Compound systems may require the application of multiple constraints simultaneously. Draw all free-body diagrams carefully and label tensions and accelerations with consistent signs.