




How to Calculate the Scalar Product of Two Vectors with Examples
The scalar product, or dot product, is a fundamental binary operation defined on pairs of vectors in Euclidean space, yielding a real-valued result that encodes both magnitude and directional alignment.
Mathematical Definition and Notation of the Scalar Product
Let $\vec{a}$ and $\vec{b}$ be two vectors in $\mathbb{R}^n$. The scalar product is denoted by $\vec{a} \cdot \vec{b}$ and is defined as the sum of products of their corresponding components:
$\vec{a} = (a_1, a_2, \ldots, a_n)$, $\vec{b} = (b_1, b_2, \ldots, b_n)$
$\vec{a} \cdot \vec{b} = a_1 b_1 + a_2 b_2 + \cdots + a_n b_n = \sum_{i=1}^{n} a_i b_i$
Alternatively, in $\mathbb{R}^3$, this operation is written in terms of the standard basis as:
$\vec{a} = a_1 \hat{\imath} + a_2 \hat{\jmath} + a_3 \hat{k}$ and $\vec{b} = b_1 \hat{\imath} + b_2 \hat{\jmath} + b_3 \hat{k}$
$\vec{a} \cdot \vec{b} = a_1 b_1 + a_2 b_2 + a_3 b_3$
Geometric Representation and Angle Dependence of the Scalar Product
For any nonzero vectors $\vec{a}$ and $\vec{b}$, making an angle $\theta \in [0, \pi]$ between them, the scalar product is given by:
$\vec{a} \cdot \vec{b} = |\vec{a}|\, |\vec{b}| \cos\theta$
Here, $|\vec{a}|$ and $|\vec{b}|$ denote the Euclidean norms, and $\theta$ is the angle measured from $\vec{a}$ to $\vec{b}$.
It follows that $\vec{a} \cdot \vec{b}$ equals the product of the magnitude of one vector and the projection of the other vector onto it.
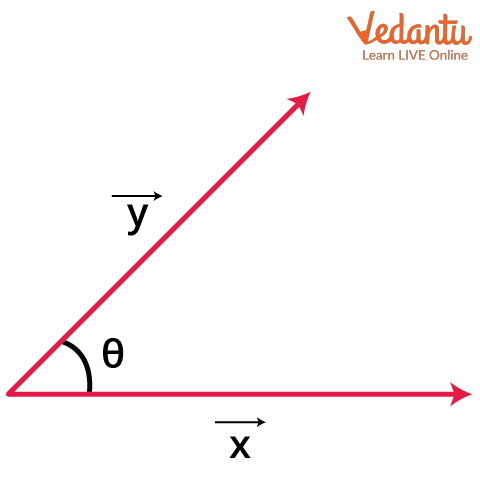
Interpretation in Terms of Projection and Orthogonality
The scalar product quantifies alignment: positive for acute angles, zero for perpendicular vectors, and negative for obtuse or antiparallel vectors.
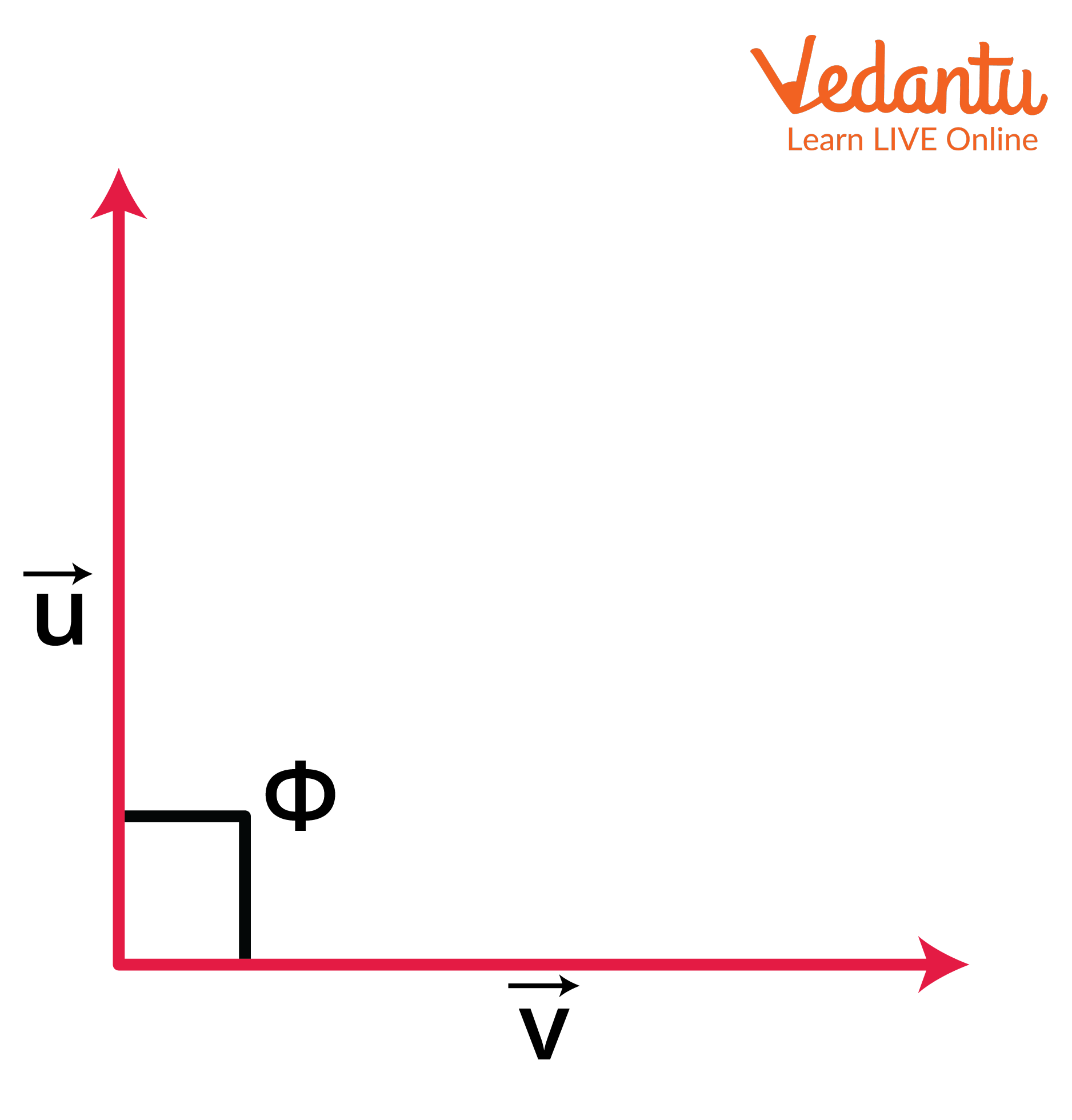

Component Evaluation and Standard Unit Vectors
The scalar products of standard basis vectors in $\mathbb{R}^3$ satisfy:
- $\hat{\imath}\cdot\hat{\imath} = \hat{\jmath}\cdot\hat{\jmath} = \hat{k}\cdot\hat{k} = 1$
- $\hat{\imath}\cdot\hat{\jmath} = \hat{\jmath}\cdot\hat{k} = \hat{k}\cdot\hat{\imath} = 0$
Hence, if two vectors are perpendicular, their dot product vanishes.
For more on foundational vector principles, refer to Vector Algebra.
Algebraic Properties Satisfied by the Scalar Product
The scalar product is symmetric and distributive over vector addition:
- Commutativity: $\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}$
- Distributivity: $\vec{a} \cdot (\vec{b} + \vec{c}) = \vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c}$
- Associativity with respect to scalar multiplication: $(\lambda\vec{a}) \cdot \vec{b} = \lambda (\vec{a}\cdot\vec{b}) = \vec{a}\cdot(\lambda\vec{b})$ for real $\lambda$
The operation is bilinear and the result is independent of coordinate system orientation.
Angle Classification Using the Scalar Product Result
| Case | $\vec{a}\cdot\vec{b}$ Value |
|---|---|
| $\theta = 0$ (Parallel, same direction) | $|\vec{a}|\,|\vec{b}|$ |
| $\theta = \pi/2$ (Perpendicular) | $0$ |
| $\theta = \pi$ (Antiparallel) | $-|\vec{a}|\,|\vec{b}|$ |
Projection of a Vector via the Scalar Product
The projection of $\vec{a}$ onto $\vec{b}$ equals:
$\mathrm{proj}_{\vec{b}}(\vec{a}) = \dfrac{\vec{a}\cdot\vec{b}}{|\vec{b}|}$
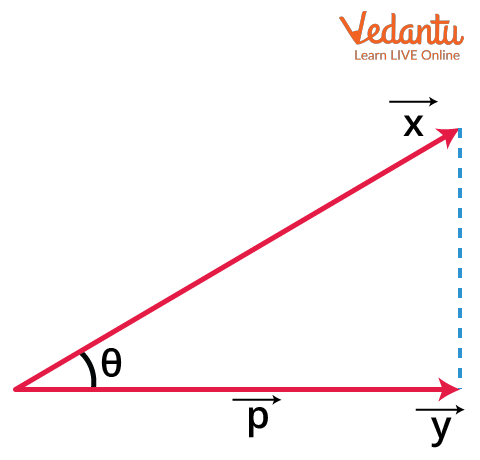
For further connection with geometric applications, see Properties of Triangle.
Evaluation of the Scalar Product: Illustrative Problems
Example 1. Given $\vec{a} = 2\hat{\imath} + 3\hat{\jmath} - 6\hat{k}$ and $\vec{b} = \hat{\imath} + 9\hat{k}$, compute $\vec{a}\cdot\vec{b}$.
Substitute components: $\vec{b} = (1, 0, 9)$
$\vec{a}\cdot\vec{b} = (2)(1) + (3)(0) + (-6)(9)$
$= 2 + 0 - 54$
Final result: $\vec{a}\cdot\vec{b} = -52$
Example 2. If $|\vec{a}| = 5$, $|\vec{b}| = 4$, and $\theta = 60^\circ$, evaluate $\vec{a}\cdot\vec{b}$.
Use definition: $\vec{a}\cdot\vec{b} = 5 \times 4 \times \cos 60^\circ$
$\cos 60^\circ = \dfrac{1}{2}$
$= 5 \times 4 \times \frac{1}{2} = 10$
Final result: $\vec{a}\cdot\vec{b} = 10$
Example 3. Show that the vectors $\vec{p} = 4\hat{\imath} + 2\hat{\jmath}$ and $\vec{q} = 2\hat{\imath} - 4\hat{\jmath}$ are not orthogonal.
$\vec{p} \cdot \vec{q} = 4 \times 2 + 2 \times (-4) = 8 - 8 = 0$
Final result: $\vec{p}$ and $\vec{q}$ are orthogonal.
Example 4. If $\vec{m} \cdot \vec{n} = 15$, $|\vec{m}| = 5$, $|\vec{n}| = 3$, find the angle between $\vec{m}$ and $\vec{n}$.
$\cos\theta = \dfrac{\vec{m}\cdot\vec{n}}{|\vec{m}|\, |\vec{n}|} = \dfrac{15}{5 \times 3} = 1$
$\implies \theta = 0^\circ$
Final result: Vectors are parallel and in the same direction.
Misconceptions and Exam Cautions Regarding the Scalar Product
- Confusing the scalar product with the vector (cross) product
- Forgetting the scalar product vanishes only for perpendicularity
- Incorrect assignment of angles outside $[0, \pi]$
- Applying dot product component formula to non-Cartesian systems
- Failure to verify the units in physical problems
For further study on advanced vector results, see the Scalar Triple Product and the Difference Between Vectors and Scalars pages.
Connections to coordinate geometry are also relevant in Geometry of Complex Numbers and Analytical Geometry.
FAQs on Understanding the Scalar Product of Vectors
1. What is the scalar product of vectors?
The scalar product of vectors, also called the dot product, is a way to multiply two vectors and obtain a scalar value. It is a fundamental operation in vector algebra used widely in physics and mathematics. The scalar product is defined as:
- A · B = |A| |B| cos θ, where θ is the angle between the vectors.
- If the vectors are perpendicular, their scalar product is zero.
- The result is a single number (scalar), not a vector.
2. How do you calculate the scalar product of two vectors?
The scalar product of two vectors can be calculated using either their magnitudes and the angle between them or their components.
Method 1: Using Magnitudes and Angle
- A · B = |A| |B| cos θ
- If A = a1i + a2j + a3k and B = b1i + b2j + b3k
- Then, A · B = a1b1 + a2b2 + a3b3
3. What are the properties of the scalar product of vectors?
The scalar product has several important properties in vector algebra:
- Commutative: A · B = B · A
- Distributive: A · (B + C) = A · B + A · C
- Scalar multiplication: (kA) · B = k(A · B)
- Zero product: The scalar product is zero if the vectors are perpendicular.
4. What is the geometric interpretation of the scalar product?
The scalar product geometrically represents the product of the magnitude of one vector and the projection of another vector onto it.
- A · B = |A| times the length of the projection of B on A.
- It measures how much one vector goes in the direction of the other.
5. When is the scalar product of two vectors zero?
The scalar product of two vectors is zero when the vectors are perpendicular (at 90° to each other).
- A · B = 0 if θ = 90°; because cos 90° = 0.
- This property helps in identifying orthogonal vectors.
- Used in exam questions involving direction cosines and geometry.
6. What is the significance of the scalar product in physics?
The scalar product is fundamental in physics for calculating work done, power, and projections.
- Work done (W) = Force · Displacement = |F| |d| cos θ
- Also helps in finding angle between vectors and resolving forces.
7. What is the difference between the scalar product and vector product?
The main difference is that the scalar product produces a scalar, while the vector product (cross product) produces a vector.
- Scalar product (dot product): A · B = |A| |B| cos θ (result is a number).
- Vector product (cross product): A × B = |A||B| sin θ n̂ (result is a vector perpendicular to both).
8. How can the scalar product be used to find the angle between two vectors?
The scalar product formula is rearranged to calculate the angle between two vectors.
- Given, A · B = |A| |B| cos θ
- θ = cos−1[(A · B)/(|A||B|)]
9. What are some examples of the scalar product of vectors in real life?
The scalar product is used in many practical situations, especially in physics.
- Calculating work done by a force.
- Finding projection of one vector onto another.
- Determining power when force and velocity are known.
10. Write the formula for the scalar (dot) product of vectors in component form.
The formula for the scalar product in component form is:
- A · B = a1b1 + a2b2 + a3b3
- Where A = a1i + a2j + a3k and B = b1i + b2j + b3k
























