How to Find the Roots of a Quadratic Equation

A quadratic equation is any equation expressible in the standard form $ax^2 + bx + c = 0$ with $a \neq 0$, where $a, b, c \in \mathbb{C}$. The values of $x$ that solve this equation are termed its roots.

Algebraic Structure and Definition of Roots for Quadratic Equations

Given $ax^2 + bx + c = 0$ ($a \neq 0$), the roots of the quadratic equation are values $\alpha, \beta \in \mathbb{C}$ such that $a\alpha^2 + b\alpha + c = 0$ and $a\beta^2 + b\beta + c = 0$.

The standard form can always be factorised (possibly over $\mathbb{C}$) as $a(x - \alpha)(x - \beta) = 0$, with both roots accounted for, potentially repeated or complex.

Derivation and Use of the Quadratic Formula

Consider $ax^2 + bx + c = 0$. Dividing through by $a$ (possible since $a \neq 0$) yields $x^2 + \frac{b}{a}x + \frac{c}{a} = 0$.

Completing the square, add and subtract $\left(\frac{b}{2a}\right)^2$ to obtain:

$x^2 + \frac{b}{a}x + \frac{b^2}{4a^2} = -\frac{c}{a} + \frac{b^2}{4a^2}$

$\left(x + \frac{b}{2a}\right)^2 = \frac{b^2 - 4ac}{4a^2}$

Taking the square root, $x + \frac{b}{2a} = \pm \frac{\sqrt{b^2 - 4ac}}{2a}$, which gives the explicit root formula:

Result: The roots are given by $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$, where $b^2 - 4ac$ is termed the discriminant.

Analysis of Root Nature via the Discriminant

Let $D = b^2 - 4ac$ be the discriminant of the quadratic equation.

• Real and unequal roots if $D > 0$
• Real and equal roots if $D = 0$
• Complex conjugate roots if $D < 0$

For $D = 0$, both roots coalesce as $x = -\frac{b}{2a}$; for $D < 0$, the two roots are complex conjugates with real part $-\frac{b}{2a}$.

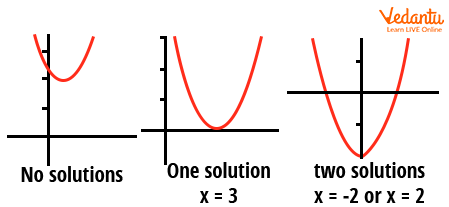
Sum and Product of Roots for Quadratic Equations

Let $\alpha$ and $\beta$ denote the roots. By direct computation:

$\alpha + \beta = \dfrac{-b}{a}$;
$\alpha \beta = \dfrac{c}{a}$.

These expressions follow from Vieta’s relations and are valid over $\mathbb{C}$ regardless of nature of roots.

A quadratic equation may always be reconstructed as $a(x^2 - (\alpha+\beta)x + \alpha\beta) = 0$ given its roots.

Primary Solution Methods for Quadratic Roots

The solution techniques for finding the roots of quadratic equations are as follows:

• Direct factorization (if factorable in the relevant domain)
• Quadratic formula (always applicable)
• Completing the square (converts to formula algebraically)
• Graphical identification (real roots via x-intercepts of the parabola)

Graphical methods are limited to real roots, while algebraic methods identify all root types.

Illustrative Solution Techniques Applied to Diverse Quadratic Equations

Example: Determine the roots of $x^2 - 7x + 10 = 0$ using all principal approaches.

(a) Factorization Method:

$x^2 - 7x + 10 = (x - 2)(x - 5) = 0$; roots are $x = 2, 5$.

(b) Quadratic Formula:

$a = 1, b = -7, c = 10$

$x = \frac{7 \pm \sqrt{(-7)^2 - 4 \times 1 \times 10}}{2}$
$= \frac{7 \pm \sqrt{9}}{2}$
$= \frac{7 \pm 3}{2} \implies x = 5, 2$

(c) Completing the Square:

$x^2 - 7x + 10 = 0$
$x^2 - 7x = -10$
$x^2 - 7x + \frac{49}{4} = -10 + \frac{49}{4}$
$(x - \frac{7}{2})^2 = \frac{9}{4}$
$x - \frac{7}{2} = \pm \frac{3}{2}$
$x = 5, 2$

Quadratic Equations Roots In Detail includes further extensions with irrational and complex examples.

Constraint-Driven Examples on Quadratic Roots

Example: Find all $k \in \mathbb{R}$ for which $3x^2 + kx + 2 = 0$ has coincident roots.

Equal roots $\Longleftrightarrow$ discriminant zero: $k^2 - 24 = 0 \implies k = \pm 2\sqrt{6}$.

Example: If $(p+1)x^2 - 2px + (q+1) = 0$ has roots $\alpha, \beta$, then $\alpha + \beta = \frac{2p}{p+1}$ and $\alpha\beta = \frac{q+1}{p+1}$.

Geometric Characterization of Quadratic Equation Roots

The graph of $y = ax^2 + bx + c$ is a parabola. Its intersection with the $x$-axis corresponds to real roots. Exam Tip: If the parabola is tangent to the $x$-axis, the roots coincide.

For further systematic exploration refer to Quadratic Equations Overview or study Quadratic Inequalities Explained for root-based inequality analysis.

Typical Errors Regarding Quadratic Roots

• Assuming all quadratics have real roots
• Incorrectly applying formula when $a = 0$
• Omitting check of discriminant for root nature
• Loss of sign in sum and product expressions
• Mistaking multiplicity for distinctness

Practice varied forms through Problems on Quadratic Equations and extend to optimization with Maxima and Minima of Quadratics.