JEE Important Chapter - Sets, Relations and Functions

In JEE Main Mathematics, Sets, Relations, and Functions are one of the most important topics as they serve as a basic building block for several other advanced concepts of Mathematics. Therefore it is a crucial chapter for students. Students can understand and solve problems based on sets, relations, and functions with the help of the solved sums, and notes PDF provided on Vedantu.

The three main concepts covered in this chapter are Functions, Sets, and Relations. Students will get a clear idea of these concepts by referring to the solutions, explanations, sets, relations, and functions notes PDF prepared by the subject matter experts at Vedantu. Also, students must learn and revise the formulas covered in this chapter thoroughly. All important concepts of this chapter will be discussed in the following sections.

JEE Main Maths Chapter-wise Solutions 2023-24 

Important Topics of Sets, Relations, and Functions

• Sets, roster and set builder form of sets

• Type of sets

• Subset, the proper and improper subset

• Power set, universal set, the union of sets, complement of sets

• De-morgan’s law

• Ordered pairs, cartesian product

• Relation and its types

• Number of relations

• The inverse of a function

Important Concepts of Sets, Relations, and Functions

What is Sets in Maths?

A set is a collection of well-defined elements or objects. The elements of a set are considered distinct.

A set of multiple sets is frequently called a family or collection of sets. For example, suppose we have a family of sets consisting of A1, A2, A3,….. up to An, that is the family {A1, A2, A3,….., An } and could be denoted as,

S = {Ai | i belongs to N and 1 ≤ i ≤ n}

Types of Sets

In set theory, there are different types of sets. Some of them are discussed below.

Singleton Set

This type of set contains only one element. For example, A = {3} and B = {pencil}. As both A and B contain only one element, they are singleton sets.

Empty Set/Null Set

An empty set is a set with no element. It is denoted by A = { } or A = ϕ.

Proper Subset

If A and B are two sets, then A is a proper subset of B if A ⊆ B, but A ≠ B, for Example: if B = {2, 3, 5} then A = {2, 5} is a proper subset of B.

Power Set

The power set is a collection of all subsets of that set. If A is the set, P(A) signifies the power set.

The number of elements contained by any power set can be calculated by n[P(A)] = 2n where n is the number of elements in set A.

For example, if A = {1, 2} then, P(A) = {∅, {1}, {2}, {1, 2}}

Number of elements in P(A) = 22 = 4

Finite Set

A set contains a finite number of elements is called Finite Set. For example: A = { 2, 4, 6, 8, 10} and B = { a, v, t}, set A has 5 objects, while set B contains 3 components. So, A and B are finite set.

Infinite Set

A set is called an infinite set if the number of elements in it is infinite. For example, N = set of whole numbers = { 0, 1, 2, 3, 4, 5, ……}

Universal Set

Any set that is a superset of all the sets being considered is called Universal set. It is commonly indicated by the letters S or U.

For example, Let P = {3, 4, 7} and Q = {1, 2, 3} then we take S = {1, 2, 3, 4, 7} as the universal set.

Equal Sets

If both P and Q are subsets of each other, they are equivalent.

Mathematically: If P ⊆ Q and Q ⊆ P then P = Q.

For example, P = {3, 6, 8} and Q = {6, 3, 8}

Here P and Q have exactly the same elements. Satisfy the conditions P ⊆ Q and Q ⊆ P.

Thus P = Q.

Operations on Sets

In Set Theory, there are basically three operations applicable to two sets.

• Union of two sets

• Intersection of two sets

• Difference of two sets

What is a Relation in Maths?

A relation in maths defines the relationship between the input and output of a function.

A subset of P X Q is a relation R that connects two non-empty sets P and Q.

For example: Let P = {a, b, c} and Q = {3, 4}

Then, R = {(a, 3), (a, 4), (b, 3), (b, 4), (c, 3), (c, 4)}

R is a subset of P x Q in this case.

So, R is a relation from P to Q.

Types of Relations

Empty Relation

There is no relation between any elements of a set is an empty relation (or void relation). For example consider, if set A = {1, 2, 3} then, one of the void relations can be R = {x, y} where, |x – y| = 8. For empty relations, R = φ ⊂ A × A.

Universal Relation

A universal (or full) relation is one in which each element of a set is related to the others. Consider set A = {a, b, c}. Now one of the universal relations will be R = {x, y} where |x – y| ≥ 0. For universal relations, R = A × A.

Identity Relation

In an identity relation, every element of a set is solely related to itself only. For example, in a set A = {a, b, c}, the identity relation will be I = {a, a}, {b, b}, {c, c}. For identity relation, I = {(a, a), a $\in$ A}.

Inverse Relation

Inverse relation is seen when a set has elements that are inverse pairs of another set. For example, consider if set A = {(a, b), (c, d)}, then the inverse relation will be R-1 = {(b, a), (d, c)}. So, for an inverse relation, R-1 = {(b, a): (a, b) $\in$ R}.

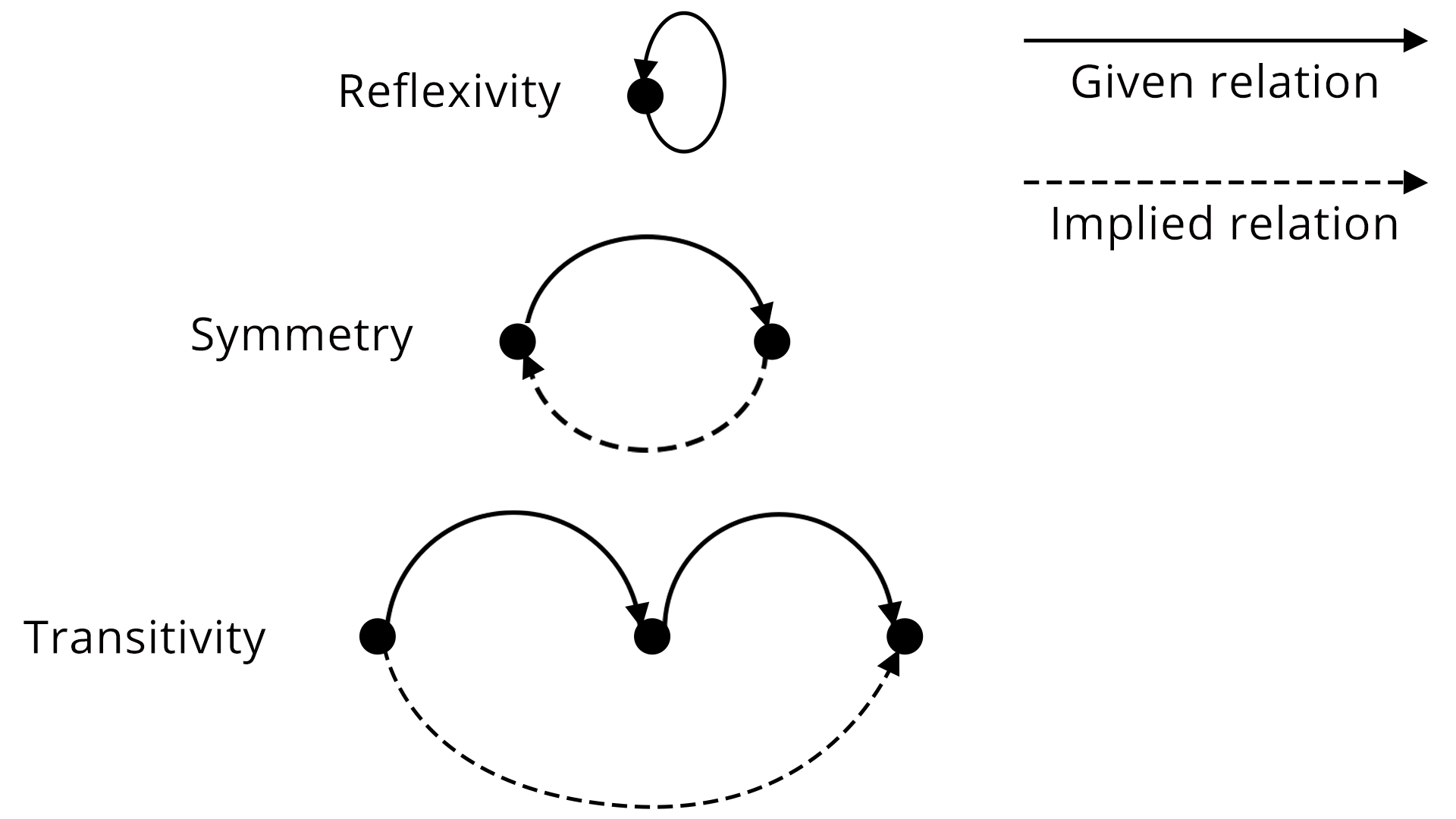
Reflexive Relation

In a reflexive relation, every element maps to itself. For example, consider a set $\text{A} = \{1, 2\}$. Now an example of reflexive relation will be $\text{R} = \{(1, 1), (2, 2), (1, 2), (2, 1)\}$. The reflexive relation is given by (a, a) $\in$ R.

Symmetric Relation

In a symmetric relation if a=b is true then b=a is also true. In other words, a relation R is symmetric only if (b, a) $\in$ R is true when (a, b) $\in$ R. An example of symmetric relation will be $\text{R}\;=\;\{(1, 2), (2, 1)\}$ for a set $\text{A}\;=\;\{1, 2\}$. So, for a symmetric relation,

aRb ⇒ bRa, ∀ a, b $\in$ A

Transitive Relation

For transitive relation, if (x, y) $\in$ R, (y, z) $\in$ R, then (x, z) $\in$ R. For a transitive relation,

aRb and bRc ⇒ aRc ∀ a, b, c $\in$ A

Equivalence Relation

If a relation is reflexive, symmetric and transitive at the same time it is known as an equivalence relation.

Domain, Co-Domain and Range of a Relation

Let A and B be two sets. In the domain, co-domain and range of a relation, if R be a relation from A to B then

• The domain of relation R (Dom(R) ) is the set of all those elements a$\in$A such that (a, b) $\in$ R for some b $\in$ B.

• If R is a relation from A to B, then B is the co-domain of R.

• Range of relation R is the set of all those elements b $\in$ B such that (a, b) $\in$ R for some a$\in$A.

In short: Domain = Dom(R) = {a : (a, b) $\in$ R} and Range (R) = {b : (a, b) $\in$ R}

Remember that Range is always a subset of co-domain.

Till now, we have learnt about Sets and Relations, now we will learn some important concepts related to Functions in maths.

Functions in Maths

A function is simply used to represent the dependence of one quantity on the other and is easily defined with the help of the concept of mapping. In simple words, a function is a relation that derives one output for each input.

A function from set P to set Q is a rule that assigns to each element of set P, one and only one element of set Q.

Mathematically: If f: A $\rightarrow$ B where y = f(x), x $\in$ P and y $\in$ Q here, y is the image of x under f.

Domain, Co-domain and Range of a Function

A function f from a set P to a set Q, represented as f: P$\rightarrow$Q, is a mapping of elements of P (domain) to elements of Q(co-domain) in such a way that each element of P is assigned to some chosen element of Q. That is every element of P must be assigned to some element of Q and only one element of Q.

Domain:

For a function, $y\;=\;f(x)$, the set of all the values of x is called the domain of the function. It refers to the set of possible input values.

Range:

The range of $y\;=\;f(x)$ is a collection of all outputs $f(x)$ corresponding to each real number in the domain. The range is the set of all the values of $\text{y}$. It refers to the set of possible output values.

For example, consider the following relation.

{(2, 3), (4, 5), (6, 7)}

Here Domain = {2, 4, 6}

Range = { 3, 5, 7}

List of Functions, Sets and Relations Formulas

Solved Sets, Relations and Functions Examples

Example 1: Find domain, co-domain and range of a Relation pRq = p divides q. If P = {3, 5, 7} and Q = {6, 12, 5, 9}.

Solution:

P = {3, 5, 7} and Q = {6, 12, 5, 9}

Since, the relation between elements of P and Q is “p divides q”, then

R = {(3, 6), (3, 12), (3, 9), (5, 5)}

Therefore, Domain(R) = {3, 5}

Co-domain of R = Q = {6, 12, 5, 9}

And, Range = {5, 6, 9, 12}

Example 2: Let a relation R be defined by R = {(4, 5); (1, 4); (4, 6); (7, 6); (3, 7)} then R−1 o R is ________.

Solution:

First, find R−1,

$R^{−1}$ = $\{(5, 4) ; (4, 1) ; (6, 4) ; (6, 7) ; (7, 3)\}$.

Obtain the elements of R−1 o R.

Pick the element of $\text{R}$ and then of $R^(-1)$.

Since (4, 5) $\in$ R and (5, 4) $\in$ R−1, we have (4, 4) $\in$ R−1 o R

Similarly, (1, 4) $\in$ R, (4, 1) $\in$ R−1 ⇒ (1, 1) $\in$ R−1 o R

(4, 6) $\in$ R, (6, 4) $\in$ R−1 ⇒ (4, 4) $\in$ R−1 o R,

(4, 6) $\in$ R, (6, 7) $\in$ R−1 ⇒ (4, 7) $\in$ R−1 o R

(7, 6) $\in$ R, (6, 4) $\in$ R−1 ⇒ (7, 4) $\in$ R−1 o R,

(7, 6) $\in$ R, (6, 7) $\in$ R−1 ⇒ (7, 7) $\in$ R−1 o R

(3, 7) $\in$ R, (7, 3) $\in$ R−1 ⇒ (3, 3) $\in$ R−1 o R,

Hence, R−1 o R = {(1, 1); (4, 4); (4, 7); (7, 4), (7, 7); (3, 3)}.

Solved Problems of Previous Year's Question Paper

Question 1: Let f, g: N→N such that f(n + 1)= f(n)+ f(1) for all n $\in$ N and g be any arbitrary function. Which of the following statements is NOT true?

1. f is one-one

2. If fog is one-one, then g is one-one

3. If g is onto, then fog is one-one

4. If f is onto, then f(n) = n for all n $\in$ N

Solution:

Answer: (c)

f(n + 1) = f(n) +f(1)

⇒ f(n + 1)- f(n)= f(1) → A.P. with common difference = f(1)

General term = Tn = f(1) + (n-1)f(1) = nf(1)

⇒f(n) = nf(1)

Clearly f(n) is one-one.

For fog to be one-one, g must be one-one.

For f to be onto, f(n) should take all the values of natural numbers.

As f(x) is increasing, f(1)=1

⇒f(n)=n

If g is many one, then fog is many one. So “if g is onto, then fog is one-one” is incorrect.

Question 2: Let R = {(P,Q)|P and Q are at the same distance from the origin} be a relation, then the equivalence class of (1,–1) is the set :

1. S = {(x, y)|x2 + y2 = 1}

2. S = {(x, y)|x2 + y2 = 4}

3. S = {(x, y)|x2 + y2 = √2}

4. S = {(x, y)|x2 + y2 = 2}

Solution:

Answer: (d)

P(a, b) , Q(c, d), OP = OQ

a2 + b2 = c2 + d2

R(x ,y), S = (1, –1) OR = OS ( equivalence class)

x2 + y2 = 2

Question 3: Let f (x) = sin-1 x and g (x) = (x2 - x - 2) / (2x2 - x - 6). If g (2) = \[\lim_{ x \to 2}\] g (x), then the domain of the function fog is:

1. (- ∞, - 2] ⋃ [- 4 / 3, ∞]

2. (- ∞, - 1] ⋃ [2, ∞)

3. (- ∞, - 2] ⋃ [- 1, ∞]

4. (- ∞, 2] ⋃ [- 3 / 2, ∞)

Solution:

Answer: (a)

g (2) = \[\lim_{ x\to 2}\] [(x - 2) (x + 1)] / [(2x + 3) (x - 2)] = 3 / 7

For the domain of f (g (x))

|(x2 - x - 2) / (2x2 - x - 6)| ≤ 1 [because of f (x) is [- 1, 1])

(x + 1)2 ≤ (2x +3)2

3x2 + 10x + 8 ≥ 0

(3x + 4) (x + 2) ≥ 0

x belongs to (- ∞, - 2] ⋃ [- 4 / 3, ∞]

Practise Problems

1. Let A = {a, b, c} and B = {1, 2}. Consider a relation R  defined from set A to set B. Then R  is equal to set:

1. A

2. B

3. $B\;\times\;A$

4. $A\;\times\;B$

2. In a class of 100 students, 55 students have passed in Mathematics and 67 students have passed in Physics. Then the number of students who have passed in Physics only is

1. 33

2. 25

3. 45

4. 10

Answers: 1 - D, 2 - C

Conclusion

Now, you will be able to answer questions about Sets, Relations, and Functions, as well as questions that ask you to use all three concepts at once. Because sets, relations, and functions are foundational concepts in calculus and a foundational concepts in many other chapters, they will aid in your understanding of many other chapters.

Study Materials for Sets, Relations and Functions:

These study materials will aid you in comprehending Sets, Relations and Functions, ensuring a solid foundation for further mathematical pursuits.

Important Links for JEE Main and Advanced 2023-24

Access a curated collection of study materials and tips to excel in JEE Main and Advanced 2023-24, helping you prepare effectively for these prestigious engineering entrance exams.