NCERT Exemplar for Class 12 Physics Chapter 1 - Electric Charges And Fields (Book Solutions)

Exercise

Multiple Choice Questions-I 

1.1 In the given figure, two positive charges $q_{2}$ and $q_{3}$ fixed along the y axis, exert a net electric force in the positive x direction on a charge $q_{1}$ fixed along the x axis.

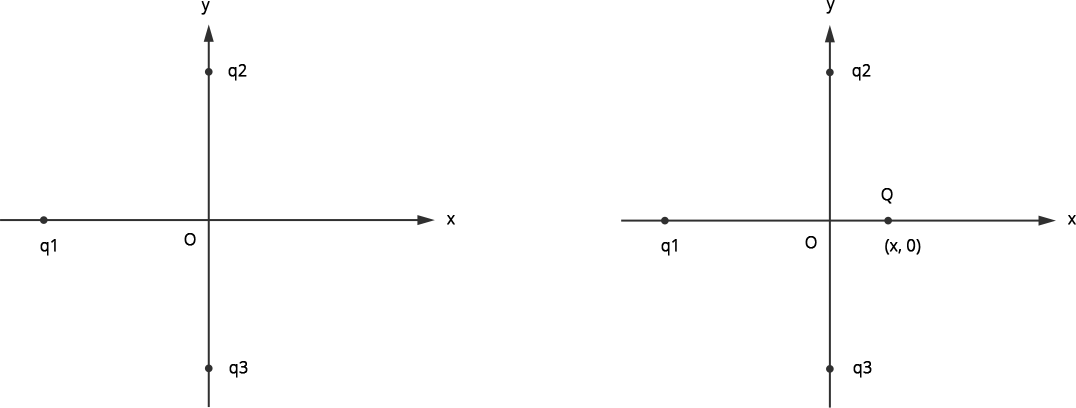
If a positive charge Q is added at (x, O), the force on $q_1$ 

(a) shall increase along the positive x-axis. 

(b) shall decrease along the positive x-axis. 

(c) shall point along the negative x-axis. 

(d) shall increase but the $q_2$ and $q_3$

Ans: option (a) 

Let the given resultant force be $R$. As $R$ is acting along positive x direction, by dividing its components along ${F_{12}}$ & ${F_{13}}$ we find that  ${F_{12}}$ & ${F_{13}}$ are acting towards ${q_2}$ & ${q_3}$ respectively.

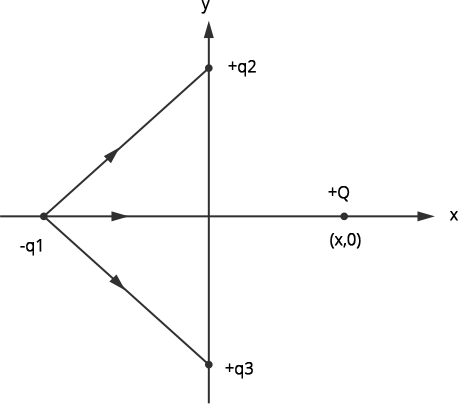
Hence, from this we conclude that  ${q_1}$ is negatively charged. As, ${q_2}$ and $ {q_3}$ are positive charges (given), when we place a positive charge Q at position (x, 0), so the force due to Q on ${q_1}$ is also along the positive x direction. Hence, the total resultant force on ${q_1}$ will increase along the positive x axis. Therefore, the correct answer is option (a).

1.2 A point positive charge is brought near an isolated conducting sphere in the given figure. The electric field is best given by

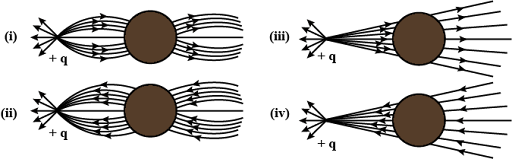
(a) Fig.(i) 

(b) Fig. (ii)

(C) Fig. (iii) 

(d) Fig. (iv)

Ans: option (a) 

When a point positive charge is brought near an isolated conducting sphere, due to the force of attraction of the point positive charge, the negative charges accumulate on the left surface of the sphere and the positive charges on the right surface. So the lines of force will be perpendicularly inward towards the left surface and perpendicularly outwards from the right surface. So the best figure, here, is (i).

1.3 The Electric flux through the surface

(a) in Fig. (iv) is the largest. 

(b) in Fig. (iii) is the least. 

(c) in Fig. (ii) is the same as Fig. (iii) but is smaller than Fig. (iv) 

(d) is the same for all the figures. 

Ans: option (d) 

As we know, according to gauss law, electric flux through a surface is given by

$\phi  = \dfrac{q}{{{\varepsilon _ \circ }}}$

Thus, electric flux is independent of the type of surface enclosing the charge. Hence, electric flux through all surfaces will be same i.e. option (d)

1.4 Five charges $q_{1}$ , $q_{2}$ , $q_{3}$ , $q_{4}$, and $q_{5}$ are fixed at their positions as shown in Figure. S is a Gaussian surface. The Gauss’s law is given by 

$\oint\limits_s {E.ds}  = \dfrac{q}{{{\varepsilon _ \circ }}}$

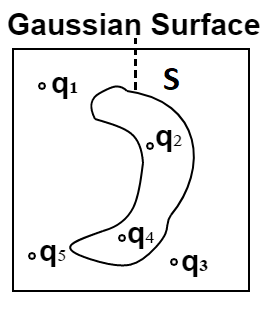
Which of the following statements is correct? 

(a) E on the L.H.S of the above equation will have a contribution from  $q_{1}$,  $q_{5}$ and  $q_{3}$ while q on the RHS will have a contribution from  $q_{2}$ and  $q_{4}$ only. 

(b) E on the L.H.S of the above equation will have a contribution from all charges while q on the R.H.S will have a contribution from  $q_{2}$ and  $q_{4}$ only. 

(c) E on the L.H.S of the above equation will have a contribution from all charges while q on the R.H.S will have a contribution from  $q_{1}$,  $q_{3}$ and  $q_{5}$ only.

(d) Both E on the L.H.S and q on the R.H.S will have contributions from  $q_{2}$ and  $q_{4}$ only.

Ans: option (b) 

From Gauss law (given) electric flux is given by,

$\phi  = \oint {E.ds = \dfrac{q}{{{\varepsilon _ \circ }}}} $

So, the q given in the RHS is the sum of all charges enclosed in the gaussian surface i.e. due to $q_2$ and $q_4$ only (from the given figure). And the electric field present in the LHS is the resultant electric field due to all the charges present inside and outside the gaussian surface. Thus, (b) is the correct option.

1.5 Figure here shows electric field lines in which an electric dipole is placed as shown. Which of the following statements is correct? 

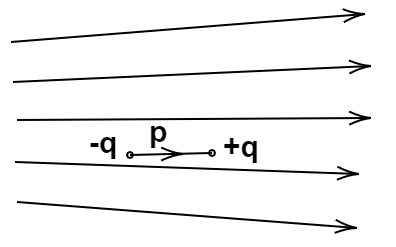
(a) The dipole will not experience any force. 

(b) The dipole will experience a force towards the right. 

(c) The dipole will experience a force towards the left. 

(d) The dipole will experience a force upwards

Ans: option (c)

According to the question, the electric field lines are non-uniform in nature denoting the decrease in intensity of field from left to right. The force on -q will be greater than the force on $+q$. The direction of force on +q is along the direction of the electric field, so force on $-q$ will be in the left direction. So, net force on the dipole will be towards the left, which verifies the answer (c).

1.6 A point charge +q, is placed at a distance ‘d’ from an isolated conducting plane. The field at a point P on the other side of the plane is 

(a) directed perpendicular to the plane and away from the plane. 

(b) directed perpendicular to the plane but towards the plane. 

(c) directed radially away from the point charge. 

(d) directed radially towards the point charge.

Ans: option (a)

Let the charge +q be positioned at the left of the given conducting plane AB which is vertical to the plane. Due to the charge +q, negative charge will accumulate on the left side of the plane and vice versa.

As, field lines due to positive charge are always perpendicularly outward in nature, so, field lines at point P will be away from the plane. Hence, (a) is the correct answer.

1.7 A hemisphere is uniformly charged positively. The electric field at a point to the diameter away from the centre is directed 

(a) perpendicular to the diameter 

(b) parallel to the diameter 

(c) at an angle tilted towards the diameter 

(d) at an angle tilted away from the diameter.

Ans: option (a)

Electric field lines are always perpendicular to the surface, and as the side of the hemisphere is a plane surface, thus, the electric field lines through the surface will also be perpendicular to the diameter. Hence, (a) is the correct answer.

Multiple choice Questions-II More than one option

1.8 If $\oint\limits_s {E.ds}  = 0$ over a surface, then 

(a) the electric field inside the surface and on it is zero. 

(b) the electric field inside the surface is necessarily uniform. 

(c) the number of flux lines entering the surface must be equal to the number of flux lines leaving it. 

(d) All charges must necessarily be outside the surface.

Ans: options (c) and (d)

According to gaussian law, flux would be zero only if all the sum or all the charges inside the surface will be zero or all the charges will be outside the surface. If the charges will be outside the surface, then the number of flux lines entering and leaving the surface will be equal, which means (c) and (d) are correct options.

1.9 The Electric field at a point is 

(a) always continuous. 

(b) continuous if there is no charge at that point. 

(c) discontinuous only if there is a negative charge at that point. 

(d) discontinuous if there is a charge at that point.

Ans: options (b) and (d)

As we know, for an isolated electric charge the electric field tends to infinity until and unless any other charges interact with the electric field of the given isolated charge. So, we can conclude that (b) and (d) are correct options.

1.10 If there were only one type of charge in the universe, then 

(a) $\oint\limits_s {E.ds}  \ne 0$ on any surface. 

(b) $\oint\limits_s {E.ds}  = 0$ if the charge is outside the surface. 

(c) $\oint\limits_s {E.ds} $ could not be defined. 

(d) $\oint\limits_s {E.ds}  = \dfrac{q}{{{\varepsilon _ \circ }}}$if charges of magnitude q were inside the surface.

Ans: options (b) and (d)

Gauss law is independent of the sign of the charge and will not change for the given conditions. Therefore, $\oint\limits_s {E.ds}  = \dfrac{q}{{{\varepsilon _ \circ }}}$ according to gauss law. And $\oint\limits_s {E.ds}  = 0$ will be only possible if the charge is outside the surface. Hence, (b) & (d) are correct options.

1.11 Consider a region inside which there are various types of charges but the total charge is zero. At points outside the region 

(a) the electric field is necessarily zero. 

(b) the electric field is due to the dipole moment of the charge distribution only. 

(c) the dominant electric field is $ \propto \dfrac{1}{{{r^3}}}$, for large ‘r’, where ‘r’ is the distance of point (outside) from an origin in this region. 

(d) the work done to move a charged particle along a closed path, away from the region, will be zero.

Ans: options (c) and (d)

Electric field at a point due to a dipole is always inversely proportional to the cube of the distance from the given point. Also, work done due to any conservative force in a closed loop is always zero. So, answer (c) and (d) are correct.

1.12 Refer to the arrangement of charges in the given figure and a Gaussian surface of radius R with Q at the centre of the surface. Then 

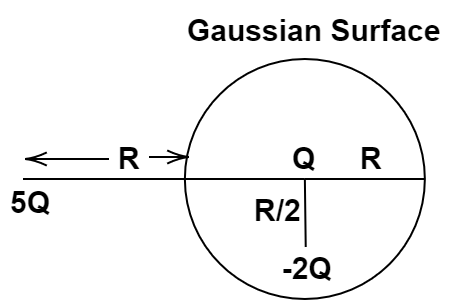
(a) total flux through the surface of the sphere is $\dfrac{{ - Q}}{{{\varepsilon _ \circ }}}$. 

(b) The field on the surface of the sphere is $\dfrac{{ - Q}}{{4\pi {\varepsilon _ \circ }{R^2}}}$. 

(c) flux through the surface of the sphere due to 5Q is zero. 

(d) field on the surface of the sphere due to -2Q is same everywhere.

Ans: options (a) and (c)

Total flux through a surface is given by

$\phi  = \dfrac{q}{{{\varepsilon _ \circ }}}$

Where, q is the total charge enclosed by the surface.

Therefore, the net charge inside the gaussian surface is $( + Q - 2Q) =  - Q$

And net flux is $\phi  = \dfrac{{ - Q}}{{{\varepsilon _ \circ }}}$

And as 5Q is outside the surface, it doesn’t contribute to the flux.

Hence (a) & (c) are correct.

1.13 A positive charge +Q is uniformly distributed along a circular ring of radius R. A small test charge q is placed at the centre of the ring (Fig.1.7). Then: 

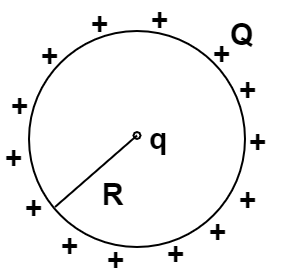
                             Fig. 1.7

(a) If $q > 0$ and is displaced away from the centre in the plane of the ring, it will be pushed back towards the centre. 

(b) If $q < 0$ and is displaced away from the centre in the plane of the ring, it will never return to the centre and will continue moving till it hits the ring. 

(c) If $q < 0$, it will perform S.H.M for small displacement along the axis. 

(d) q at the centre of the ring is in an unstable equilibrium within the plane of the ring for $q > 0$. 

Ans: options (a), (b) and (c) 

If $q<0$ then when it will be displaced the net force will increase for one side and decrease for the other. Thus, it will not be pushed back towards the centre.

When the point charge is displaced towards the axis it’ll be attracted by Q and hence will try to return back to its normal position. But due to the kinetic energy, it will cross the centre and will again experience force of attraction from Q. Hence, it’ll continue SHM.

When $q>0$, if it’ll be displaced it’ll experience repulsive force from Q on both sides which will be unequal. Hence, it’ll be pushed back towards the centre. Therefore, (a), (b) and (c) are correct options.

Very Short Answer Type Questions

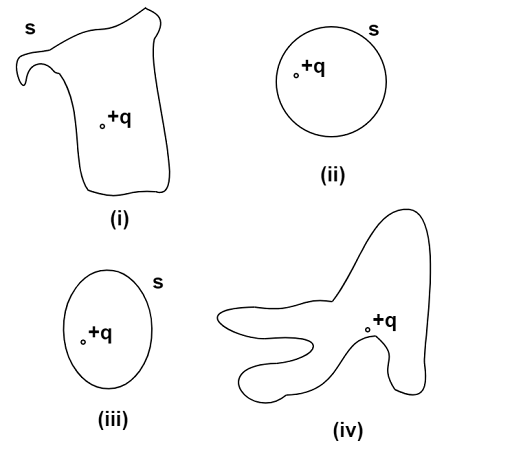
1.14 An arbitrary surface encloses a dipole. What is the electric flux through this surface?

Ans: The net charge of a dipole is always zero.

Also, according to gauss law

$\phi  = \oint\limits_s {E.ds}  = \dfrac{q}{{{\varepsilon _ \circ }}}$

As ‘$ + q - q = 0$’ is the net charge enclosed inside the gaussian surface. Therefore, the electric flux through the gaussian surface is also zero.

1.15 A metallic spherical shell has an inner radius $R_{1}$ and outer radius $R_{2}$ . A charge Q is placed at the centre of the spherical cavity. What will be surface charge density on (i) the inner surface, and (ii) the outer surface?

Ans: Due to the positive charge +Q in the centre, negative charge -Q will accumulate on the inner surface and +Q will accumulate on the outer surface.

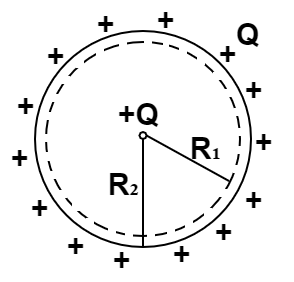
$\sigma $= Surface charge density = $\dfrac{Q}{{Area}}$

$\sigma $ on inner surface = $\dfrac{{ - Q}}{{4\pi {R_1}^2}}$

$\sigma $ on outer surface = $\dfrac{{ + Q}}{{4\pi {R_2}^2}}$

1.16 The dimensions of an atom are of the order of an Angstrom. Thus, there must be large electric fields between the protons and electrons. Why, then, is the electrostatic field inside a conductor zero?

Ans: As for an isolated conductor, the number of electrons is equal to the number of protons inside the conductor. In the absence of excess charge the electrostatic field is given by: $E = \dfrac{{kq}}{{{r^2}}}$

As $q = 0$, so the electrostatic field inside a conductor is zero.

1.17 If the total charge enclosed by a surface is zero, does it imply that the electric field everywhere on the surface is zero? Conversely, if the electric field everywhere on a surface is zero, does it imply that net charge inside is zero?

Ans: By Gauss’s law

$\oint\limits_s {E.ds}  = \dfrac{q}{{{\varepsilon _ \circ }}}$

The electric field in the above equation is independent of the charge enclosed within the gaussian surface. For example, it may be possible that two equal and opposite charges be present inside the gaussian surface and an independent charge may be present outside the gaussian surface, then the electric field by the equal and opposite charges will be zero but the independent charge will have its own influence on the net electric field. Thus, the electric field will not be zero. But conversely, if the net given electric field is zero, it is necessary that the net sum of charges will be zero.

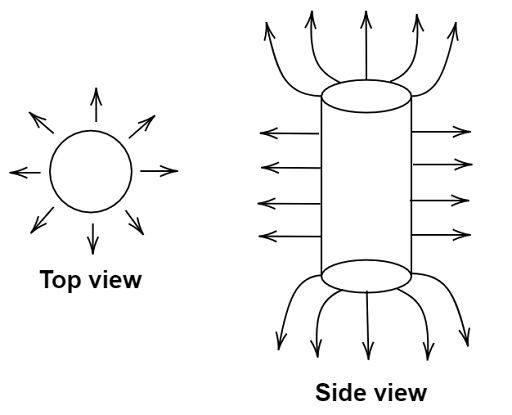
1.18 Sketch the electric field lines for a uniformly charged hollow cylinder shown in Fig 1.8.

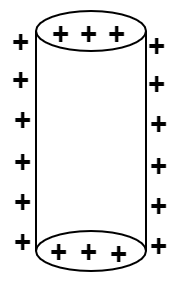
Ans: As there is only positive charge present on the surface of the cylinder the electric field lines will be perpendicular and outward in nature.

1.19 What will be the total flux through the faces of the cube $\left( {{{Fig}}.{\text{ }}{{1}}.{{9}}} \right)$with side of length if a charge $q$ is placed at

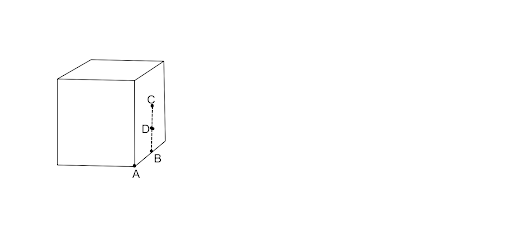
         Fig. 1.9

(a) A; a corner of the cube. 

Ans: (a) Let us assume a cube of side 2a with charge placed at the centre of the cube at A. If the cube will be divided into 8 cubes of side a, then the charge will be equally distributed among the 8 cubes Therefore, the total flux through the faces of the cube =$\dfrac{q}{{8{\varepsilon _0}}}$

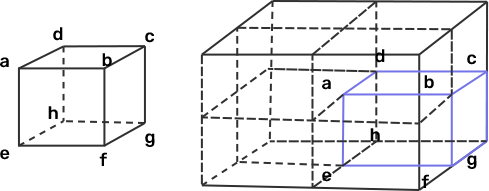
(b) B; mid-point of an edge of the cube.

Ans: According to the question the charge is placed at B, so the charge will be distributed among 4 cubes of side a. Hence, the total flux through the four faces is $\dfrac{q}{{4{\varepsilon _0}}}$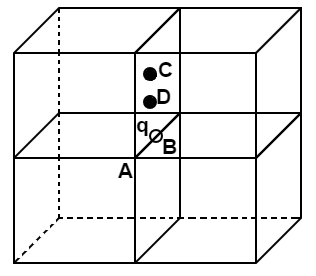

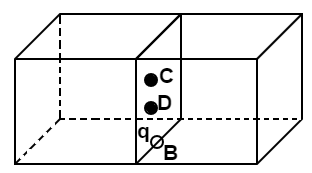
(c) C; centre of a face of the cube.

Ans: If the charge is placed at C, centre of the face of the cube , then the charge will be distributed among 2 cubes of side a, therefore the total flux will be $\dfrac{q}{{2{\varepsilon _0}}}$

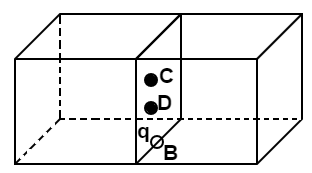
(d) D; mid-point of B and C.

Ans: If the charge is placed at D, Which is the midpoint of B and C so the charge will be distributed among two cubes of side a  and therefore, the flux through them will be $\dfrac{q}{{2{\varepsilon _0}}}$

Short Answer Type Questions

1.20 A paisa coin is made up of Al-Mg alloy and weighs $0.75g$. It has a square shape and its diagonal measures $17{\text{ }}mm$. It is electrically neutral and contains equal amounts of positive and negative charges. Treating the paisa coins made up of only Al, find the magnitude of an equal number of positive and negative charges. What conclusion do you draw from this magnitude? 

Ans: The given mass of 1 paisa coin is $0.75g$.

Molar mass of Al is $27g$.

So, the no. of moles of Al in 1 paisa coin =$\dfrac{{0.75}}{{27}}$

Now the no of atoms of Al in 1 paisa coin =$\dfrac{{0.75 \times 6.023 \times {{10}^{23}}}}{{27}}$

Now the no of electrons or protons in one Al atom = atomic no. of Al atom =$13$

no of electron in 1 paisa coin = $\dfrac{{0.75 \times 6.023 \times {{10}^{23}} \times 13}}{{27}}$

charge of one electron = $1.6 \times {10^{ - 19}}$

charge of electrons in 1 paisa coin =$\dfrac{{0.75 \times 6.023 \times {{10}^{23}} \times 13 \times 1.6 \times {{10}^{19}}}}{{27}}$

=$3.48 \times {10^4}C$

Either positive or negative charge on a coin= 34.8 KC 

It concludes that a 1 paisa coin contains an enormous amount of positive and negative charges which are equal in magnitude.

1.21 Consider a coin of Example 1.20. It is electrically neutral and contains equal amounts of positive and negative charge of magnitude 34.8 kC. Suppose that these equal charges were concentrated in two point charges separated by 

(i) 1 cm (~1/2× diagonal of one paisa coin), (ii) 100 m (~ length of a long building), and (iii) ${10^6}$ m (radius of the earth). Find the force on each such point charge in each of the three cases. What do you conclude from these results?

Ans: Each point charge is considered as separated entities and are placed in a distance according to the given question. And by coulomb’s law we define the force of attraction between two charges as :-

$F = \dfrac{{q1q2}}{{4\pi {\varepsilon _ \circ }{r^2}}}$

Where, $q_1$ and $q_2$ are two charges with magnitude $34.8\,kc$.

Now taking out force of attraction of two point charges with separation 

(i) At ${r_1} = {10^{ - 2}}$m

F=$\dfrac{{|q{|^2}}}{{4\pi {\varepsilon _ \circ }{r_1}^2}}$=$\dfrac{{34.8 \times {{10}^{ - 9}} \times 9 \times {{10}^9}}}{{{{({{10}^{ - 2}})}^2}}}$=$\;\;\;1.09 \times {10^{23}}N$

(ii) At  ${\text{ }}{r_2} = {\text{ }}100m$

F=$\dfrac{{|q{|^2}}}{{4\pi {\varepsilon _ \circ }{r_2}^2}}$=$\dfrac{{34.8 \times {{10}^{ - 9}} \times 9 \times {{10}^9}}}{{{{(100)}^2}}}$= $\;\;\;1.09 \times {10^{15}}N$

(iii) At ${r_3} = {10^6}m$

$F=\dfrac{{|q{|^2}}}{{4\pi {\varepsilon _ \circ }{r_2}^2}}=\dfrac{{34.8 \times {{10}^{ - 9}} \times 9 \times {{10}^9}}}{{{{({{10}^6})}^2}}}= 1.09 \times {10^7}N$

Therefore, we can observe that when ± charges in ordinary neutral matter are separated as point charges, they exert an enormous force. Hence, it needs a lot of force electrical neutrally of matter. And we can conclude that gravitational forces are weaker than the coulomb’s force of attraction.

1.22 Fig. shows a crystal unit of caesium chloride, CsCl. The caesium atoms, represented by open circles, are situated at the corners of a cube of 0.40nm, whereas a Chlorine atom is situated at the centre of the cube. The caesium atoms are deficient in one electron while the Cl atom carries an excess electron.

(i) What is the net electric field (force) on the Cl atom due to eight Cs atoms?

Ans: According to the question as crystal of CsCl-, caesium atoms are containing a positive charge and Cl- atom has a negative charge and magnitude of both charges are equal to e. The Cl - ion is in the middle of the crystal lattice and its separation from the Cs+ ion is equal to 

$\dfrac{1}{2}$.......(Diagonal of the cube of side $0.40nm$)

$d= \dfrac{1}{2}\sqrt {3{l^2}} $

$d = \dfrac{1}{2}\sqrt {3 \times 0.4 \times {{10}^{ - 9}} \times 0.4 \times {{10}^{ - 9}}} m$

$d =\dfrac{1}{2} \times 0.4 \times {10^{ - 9}} \times \sqrt 3 $ m

$d = 0.2\sqrt 3  \times {10^{ - 9}}m$.

The distance of Cl –  and Cs+ ion is $0.2\sqrt 3  \times {10^{ - 9}}m$

The net electric field due to each Cs+ ion forms a resultant of zero. Force component of each Cs+ ion gets cancelled due to the force component of Cs+ ion placed at the opposite corner, as each force component is equal in magnitude but opposite in direction. Hence the net electric field at the middle of the diagonal is zero.

(ii) Suppose that the Cs atom at the corner A is missing. What is the net force on the Cl atom due to seven remaining Cs atoms?

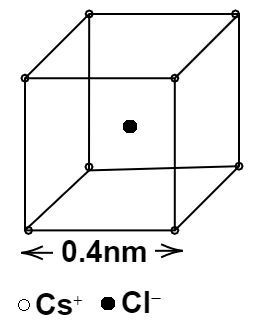
Ans: Now one of the Cs+ ions is missing so a new net electric field will appear at the middle of the diagonal. and Cl –  ion will experience some force. As Cs+ ion at A gets removed the force due to Cs+ ion at the corner opposite to corner A will appear in the net force, and the force due to the other ions gets cancelled. 

Now net force on Cl –  ion due to the Cs+ ion after Cs+ ion at corner opposite to corner A is =$\dfrac{{q_1q_2}}{{4\pi {\varepsilon _ \circ }{r^2}}}$ 

where $q_1$ and $q_2$ are charges of Cl – and Cs+ ions of equal magnitude.

Given , r= $0.2\sqrt 3  \times {10^{ - 9}}m$.|q|=$1.6 \times {10^{ - 19}}C$.

$F = \dfrac{{9 \times {{10}^9} \times 1.6 \times {{10}^{ - 19}} \times 1.6 \times {{10}^{ - 19}}}}{{0.2\sqrt 3  \times {{10}^{ - 9}} \times 0.2\sqrt 3  \times {{10}^{ - 9}}}}$

$F = \dfrac{9 \times 16 \times 16 \times {{10}^{ - 29}}}{2 \times 2 \times 3 \times {{10}^{ - 18}}}$

$F = 192 \times 10^{ - 11}$$N$

Force on Cl –  ion is 

$F = 1.92 \times {10^{ - 9}}N$

And this force acts towards $Cl^{-}$ ion.

1.23 Two charges q and –3q are placed fixed on the x-axis separated by distance ‘d’. Where should a third charge ‘2q’ be placed such that it will not experience any force?

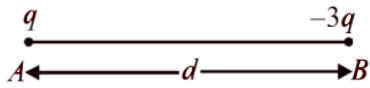
Ans: From the above question given we have three cases to look after. 

Considering the first case we find that if we place the charge $2q$ in the middle of the two charges then it will experience force in the same direction. As in the diagram, charge at A forces charge at C towards left and charge at B attracts the charge $2q$ towards left, making the net force non zero.

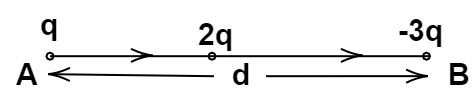
Now taking the second case in consideration, if $2q$ is placed the right side of B  

then according to coulomb’s law F=$\dfrac{{q1q2}}{{4\pi {\varepsilon _ \circ }{r^2}}}$ which implies the force of $q$ on $2q$ will decrease and the force due to $ - 3q$ increases as force is inversely proportional to distance and directly proportional to magnitude of charge.

After observing the above cases we finally come to the third case in which the 2q is placed at the left of q. 

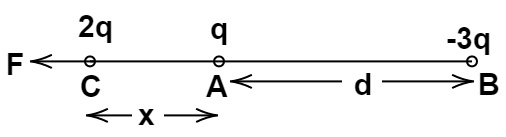
${F_{CA}} + {F_{CB}} = 0$

$\dfrac{{k{q_C}{q_A}}}{{{r^2}_{CA}}} =- \dfrac{{k{q_C}{q_B}}}{{{r^2}_{CB}}}$

$\dfrac{{2q.q}}{{{x^2}}}$=$\dfrac{{ - 2q( - 3q)}}{{{{(x + a)}^2}}}$

$\dfrac{2}{{{x^2}}}$=$\dfrac{3}{{{{(x + a)}^2}}}$

${\text{3}}{{\text{x}}^2}{\text{ = }}{{\text{x}}^2}{\text{ + }}{{\text{d}}^2}{\text{ + 2xd}}$

Now the quadratic equation is ${\text{2}}{{\text{x}}^2}{\text{ - 2xd - }}{{\text{d}}^2}{\text{ = 0}}$, by solving this equation we get,

x=$\dfrac{{ + 2a \pm \sqrt {{{( - 2d)}^2} - 4.2.( - {d^2})} }}{{2.2}}$

x=$\dfrac{{2d \pm 2d\sqrt 3 }}{4}$

Hence by simplification we can conclude that the required distance to nullify the forces is x=$\dfrac{{d \pm d\sqrt 3 }}{2}\,m$ to the left of q.

1.24 Fig. shows the electric field lines around three point charges A, B and C.

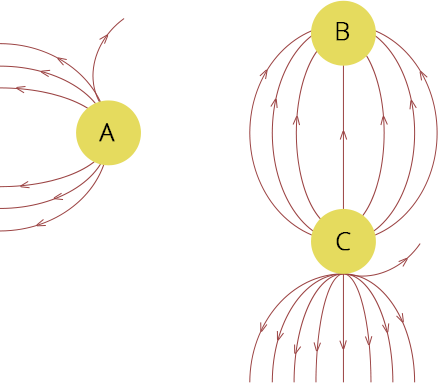
(a) Which charges are positive?

Ans: Direction of field lines denote the type of charge present, according to     convention, field lines emerge from the positive charges and merge into negative charges hence, according to the figure, charge A and charge C are positive charges.

(b) Which charge has the largest magnitude? Why?

Ans: As we know the density of field lines decides the strength of the electric field at any certain point. and by observing the figure we can conclude that field lines in charge C emerge out with highest density hence electric field due to charge C is the highest and as E is directly proportional to magnitude of charge making magnitude of charge C is maximum.

(c) In which region or regions of the picture could the electric field be zero? Justify your answer. (i) near A, (ii) near B, (iii) near C, (iv) nowhere.

Ans: Neutral point always lies between two like charges, where the electric field is zero and no electric field lines are present there. Now in the given question, only A and C are like charges and their electric field lines repel each other and form a point where electric field intensity is zero and as charge C has higher magnitude hence the neutral point lies near charge A. Thus option (i) is correct.

1.25 Five charges, q each is placed at the corners of a regular pentagon of side ‘a’ as

shown in figure.

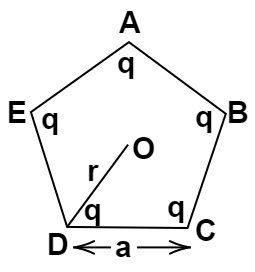
(a) (i) What will be the electric field at O, the centre of the regular pentagon?

Ans: Due to symmetry at the point O the forces due to the equal and opposite charges at the corner of regular polygon will cancel each other and make the net resultant zero.

(a)(ii) What will be the electric field at O if the charge from one of the corners (say A) is removed?

Ans: when a charge q is removed from A from one of the polygons the net electric field is due to the rest of the charges in the direction of A and equal to

$E = \dfrac{{ - q}}{{4\pi {\varepsilon _ \circ }{r^2}}}$

(a)(iii) What will be the electric field at O if the charge q at A is replaced by –q?

Ans: When the charge q at A is replaced by -q charge then the electric field at O is increased. As charge q is removed the net electric field is towards A 

${E_{}} = \dfrac{{ - q}}{{4\pi {\varepsilon _ \circ }{r^2}}}$ 

Now when a new charge -q is added at point A then the net electric field increases towards A by $\dfrac{{ - q}}{{4\pi {\varepsilon _ \circ }{r^2}}}$ making net electric field equal to

${E_1} = \dfrac{{ - q}}{{4\pi {\varepsilon _ \circ }{r^2}}} + E$

${E_1} = \dfrac{{ - 2q}}{{4\pi {\varepsilon _ \circ }{r^2}}}$ towards A.

(b) How would your answer to (a) be affected if Pentagon is replaced by the n-sided

regular polygon with charge q at each of its corners?

Ans: Now when the pentagon is replaced by the n-sided polygon.

(i) Electric field at ‘O’ will be zero again as all charge distribution about O is symmetric as in the pentagon given above the net electric field is zero.

(ii) The electric field at O will be same as in an (ii)  which will be equal to $E = \dfrac{{ - q}}{{4\pi {\varepsilon _ \circ }{r^2}}}$  , direction is towards A.

(iii)  when a new charge -q is added at point A and +q removed, then in the N sided polygon then the net electric field increases towards A by $\dfrac{{ - q}}{{4\pi {\varepsilon _ \circ }{r^2}}}$ making net electric field equal to ${E_1} = \dfrac{{ - q}}{{4\pi {\varepsilon _ \circ }{r^2}}} + E$

${E_1} = \dfrac{{ - 2q}}{{4\pi {\varepsilon _ \circ }{r^2}}}$ towards A.

Long Answer Type Questions

1.26 In 1959 Lyttleton and Bondi suggested that the expansion of the Universe could be explained if matter carried a net charge. Suppose that the Universe is made up of hydrogen atoms with a number density N, which is maintained a constant. Let the charge on the proton be: $e_{p}=-(1+y)e$ where e is the electronic charge.

(a) Find the critical value of y such that expansion may start.
Ans:(a) Let assume the universe to be spherical with radius R. Now as given in the question the universe is made of hydrogen atoms so we assume that the hydrogen atom is uniformly distributed in the universe.

Charge on proton as given in the question $ = \; - \left( {1 + y} \right)e$
So the total charge on H atom =$charge{\text{ }}of{\text{ }}electron + charge{\text{ }}of{\text{ }}proton$ = ${e_H} = {e_{P}}+e$

$ = \left( {1 + y} \right)e + e$

$ = \left[ { - 1 - y + 1} \right]e$
$ =  - ye$

So the charge of 1 hydrogen atom  $ =  - ye$
The total no. of  H atoms in the universe = $density{\text{ }} \times volume\;$=$\dfrac{4}{3}\pi {R^3}N$

The total charge in the Universe =$total{\text{ }}no{\text{ }}Of{\text{ }}H{\text{ }}atoms \times \;charge{\text{ }}of{\text{ }}a{\text{ }}H{\text{ }}atom$=$\dfrac{4}{3}\pi {R^3}N( - ye)$
Consider the Universe as Gaussian surface then by applying the  Gauss's law of electrostatics,

$\oint {zE \cdot ds = {\varepsilon _ \circ }q} $

$E.4\pi {R^2} = \dfrac{{ - 4\pi N{R^3}ye}}{{3{\varepsilon _0}}}$
$E = \dfrac{{ - 4\pi N{R^3}ye}}{{3{\varepsilon _0}4\pi {R^2}}} = \dfrac{{ - NRye}}{{3{\varepsilon _0}}}$​

Coulomb’s force due to 1 H atom  $ = {F_c} = qE$
${F_c} = \dfrac{{( - ye)( - NRye)}}{{3{\varepsilon _0}}} = \dfrac{{{y^2}eN.R}}{{3{\varepsilon _0}}}$
The force is a repulsive force as the sign is positive. The gravitational potential is given by the formula $\dfrac{{GM}}{{{R^2}}}$.

Where, $G$= universal gravitational constant, $M$= mass of the universe, $R$=radius of the universe.
Now ,gravitational force = $gravitational{\text{ }}potential{\text{ }} \times {\text{ }}mass{\text{ }}of{\text{ }}H{\text{ }}atom$
=${F_G} = \dfrac{{GM}}{{{R^2}}}{m_H}$
Mass of 1 H atom $ \approx $ mass of protons=${m_p}$
Mass of Universe(M) = No. of H atoms in Universe ×mass of 1 H atom$ = \dfrac{{4.N\pi {R^3}.{m_p}}}{3}$
Now , gravitational force = ${F_G} = \dfrac{{GM}}{{{R^2}}}{m_H}$

Putting the values, we get, ${F_G} = \dfrac{{4\pi GNRm_p^2}}{3}$

For the universe to expand the ${F_c} > {F_G}$, so for critical value of y, 

${F_c} = {F_G}$
${y^2} = 4\pi {\varepsilon _0}G{\left( {\dfrac{{{m_p}}}{e}} \right)^2}$

By putting all the values,

${y^2} = 74.1 \times {10^{ - 22}} \times {10^{ - 16}}$
$y = \sqrt {74.1 \times {{10}^{ - 38}}}  = 8.6 \times {10^{ - 19}} \simeq {10^{ - 18}}$
So, for the universe to expand, the value of y should be of the order ${10^{ - 18}}$.

(b) Show that the velocity of expansion is proportional to the distance from the Consider that the Universe is spherical with radius R made up of H atoms.

Ans: The net force experienced by the H atom is  

$F = {F_C} - {F_G} = \dfrac{{N{y^2}{e^2}R}}{{3{\varepsilon _0}}} - \dfrac{{4\pi Gm_p^2NR}}{3}$

Due to the net resultant force the H atom will experience an acceleration that is given by,
$F = {m_p}\dfrac{{{d^2}R}}{{d{t^2}}} = \left[ {\dfrac{{N{y^2}{e^2}}}{{3{\varepsilon _0}}} - \dfrac{{4\pi GNm_p^2}}{3}} \right]R$

$\dfrac{{{d^2}R}}{{d{t^2}}} = \dfrac{1}{{{m_p}}}\left[ {\dfrac{{N{y^2}{e^2}}}{{3{\varepsilon _0}}} - \dfrac{{4\pi GNm_p^2}}{3}} \right]R$

Now as the R.H.S contains most the term which is constant so we can represent it with a constant ${\alpha ^2}$

${\alpha ^2} = \dfrac{1}{{{m_p}}}\left[ {\dfrac{{N{y^2}{e^2}}}{{3{\varepsilon _0}}} - \dfrac{{4\pi GNm_p^2}}{3}} \right]$ 

So,  $\dfrac{{{d^2}R}}{{d{t^2}}} = {\alpha ^2}R$

The solution of the above equation is given by $R = A{e^{\alpha t}} + B{e^{ - \alpha t}}$

As we are dealing with expansion of the universe therefore the second term of the solution should be 0

$R = A{e^{\alpha t}}$

So, the Velocity of expansion is given by,

$v = \dfrac{{dR}}{{dt}} = A\alpha {e^{at}} = R\alpha $

Hence, $v \propto R$, i.e., velocity of expansion is proportional to the distance from the Centre.

1.27 Consider a sphere of radius R with charge density distributed as

$\rho (r) = kr$ (for$r \leqslant R)$

$\rho (r) = 0$ (for$r > R)$

(a) Find the electric field at all points r. 

Ans: Let’s take a gaussian surface of radius $r <R$. Then by applying gauss law of electrostatics,

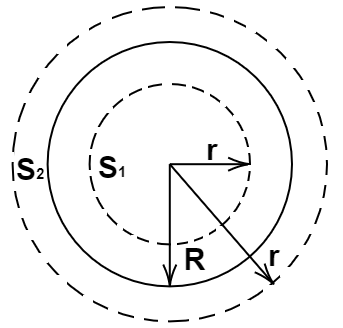
$q = density \times volume$

i.e., $q = \rho (r).\dfrac{4}{3}\pi {r^3}$

$\oint\limits_s {E.ds}  = \dfrac{1}{{{\varepsilon _ \circ }}}\rho (r).dv$

$ v = \dfrac{4}{3} \, \pi {r^3}  \\ dv = \dfrac{4}{3} \, \pi  \cdot 3{r^2}dr = 4\pi {r^2}dr  \\ $

$\rho (r) = kr$ for r < R

$\oint\limits_s {E.ds}  = \int\limits_0^r {\dfrac{{kr \cdot 4\pi {r^2}dr}}{{{\varepsilon _ \circ }}}}   \\\Rightarrow E4\pi {r^2} = \dfrac{{4\pi k}}{{{\varepsilon _ \circ }}}\int\limits_0^r {{r^3} \cdot dr}   \\ $

$ \Rightarrow E = \dfrac{{4\pi k}}{{4\pi {r^2}{\varepsilon _ \circ }}} \cdot \dfrac{{{r^4}}}{4}  \\\Rightarrow E = \dfrac{{k{r^2}}}{{4{\varepsilon _ \circ }}} $

Here, the electric field is positive, that means the direction of E is radially outward.

Case II: now we take a Gaussian surface of radius r>R(r1 in the below figure)

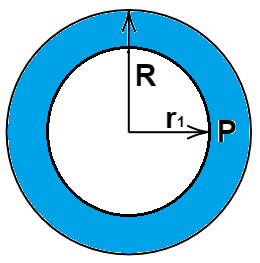
The charge still is in between r=0 to r=R .so, charge in this Gaussian surface

$q = \rho (r).dv$

$q = \int\limits_0^R {kr4 \, \pi {r^2}dr} $ because charge is present only up to radius R

By Gaussian law,

$\oint_s {E.ds}  = \dfrac{1}{{{\varepsilon _0}}}\rho (r).dv$

$\oint\limits_{ds = 4\pi {r^2}} {E.ds}  = \int\limits_0^R {\dfrac{{k \cdot 4\pi {r^3}dr}}{{{\varepsilon _ \circ }}}}   \\\Rightarrow E4\pi {r^2} = \dfrac{{4\pi k}}{{{\varepsilon _ \circ }}}\left[ {\dfrac{{{r^4}}}{4}} \right]_0^R  \\ $

$\Rightarrow E = \dfrac{{4\pi k}}{{{\varepsilon _ \circ }(4\pi {r^2})}}\left[ {\dfrac{{{R^4} - 0}}{4}} \right]  \\\Rightarrow E(r) = \dfrac{k}{{4{\varepsilon _0}}}.\dfrac{{{R^4}}}{{{r^2}}}  \\ $

The direction of the electric field is radially outwards.

(b) Suppose the total charge on the sphere is 2e where e is the electron charge. Where can two protons be embedded such that the force on each of them is zero? Assume that the introduction of the proton does not alter the negative charge distribution.

Ans: In the given sphere of radius R, a negative charge of magnitude 2e is distributed symmetrically. So, two protons must be on the opposite side equidistant from the centre. 

Charge on the sphere = $q = \rho (r).dv$

$q = \int\limits_0^R {kr \cdot 4\pi {r^2}dr}  = 4\pi k\dfrac{{{R^4}}}{4}  \\$

$2e = \pi k{R^4}$

$k = \dfrac{{2e}}{{\pi {R^4}}}$

Let the distance of the protons from the centre of the sphere O be r, Electric field due to charge distribution inside the charged sphere at r

$E = \dfrac{{k{r^2}}}{{4{\varepsilon _0}}}$

 the attractive force because of charge distribution on 1 proton is:

${F_1} =  - eE = \dfrac{{ - ek{r^2}}}{{4{\varepsilon _0}}}$

F 2=Repulsive force on proton 1 due to proton 2 according to Coulomb’s law

${F_2} = \dfrac{{{e^2}}}{{4\pi {\varepsilon _0}{{(2r)}^2}}}$

Net force on proton 1, F=F1+F2=0

${F_{}} = \dfrac{{ - ek{r^2}}}{{4{\varepsilon _0}}} + \dfrac{{{e^2}}}{{4\pi {\varepsilon _0}{{(2r)}^2}}} = 0$

$\dfrac{{ek{r^2}}}{{4{\varepsilon _0}}} = \dfrac{{{e^2}}}{{4\pi {\varepsilon _0}4{r^2}}}$

${r^4} = \dfrac{{{e^2}4{\varepsilon _0}}}{{4\pi {\varepsilon _0}4ek}}$

${r^4} = \dfrac{e}{{4\pi k}}$

${r^4} = \dfrac{{e\pi {R^4}}}{{4\pi 2e}}$          as $k = \dfrac{{2e}}{{\pi {R^4}}}$

${r^4} = \dfrac{{{R^4}}}{8}$

$r = \dfrac{R}{{8}^{¼}}$

So, protons must be embedded at a distance of $r = \dfrac{R}{{8}^{¼}}$ from the centre of the sphere of radius R.

1.28 Two fixed, identical conducting plates (α &β), each of surface area S are charged to –Q and q, respectively, where Q > q > 0. A third identical plate (γ), free to move is located on the other side of the plate with charge Q at a distance d (Fig 1.13). The third plate is released and collides with the plate β. Assume the collision is elastic and the time of collision is sufficient to redistribute charge amongst β &γ.

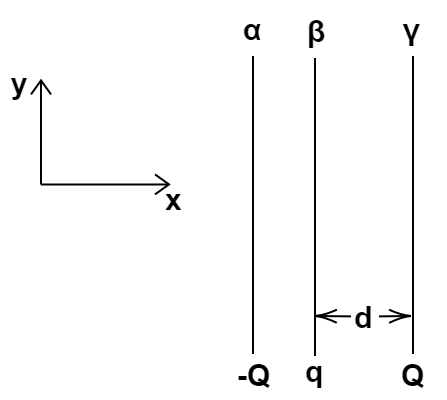
(a) Find the electric field acting on the plate γ before the collision. 

Ans: As per the question the plate γ has negative Q charge. So, electric field on plate γ due to plate α

${E_\alpha } = \dfrac{\sigma }{{2{\varepsilon _0}}} = \dfrac{{ - Q}}{{2S{\varepsilon _0}}}$

${E_\alpha } = \dfrac{{ - Q}}{{2S{\varepsilon _0}}}$ towards left

And the electric field on γ due to plate β 

=${E_\beta } = \dfrac{{ + q}}{{2S{\varepsilon _0}}}$ towards the right.

So, the resultant electric field on plate  $\gamma  = E = {F_\alpha } + {E_\beta }$

$E = \dfrac{{ - Q}}{{2S{\varepsilon _0}}} + \dfrac{q}{{2S{\varepsilon _0}}}$

${E_{}} = \dfrac{{[q - Q]}}{{2S{\varepsilon _0}}}$ 

The direction of net electric field before the collision will be ${E_{}} = \dfrac{{[q - Q]}}{{2S{\varepsilon _0}}}$  acting towards left because (Q>q)

(b) Find the charges on β and γ plates after the collision.

Ans: When plates β and γ collide, their potential becomes the same. Suppose during collision at any point P between plates β and γ the charges on β and γ plates are q1 and q2 respectively. Consider a point O in between the two plates such that the resultant electric field at O is zero.

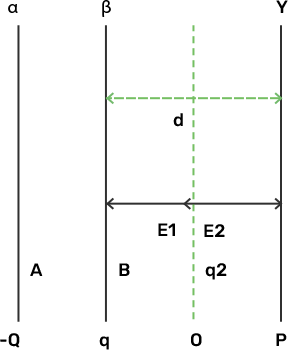
Electric field at O due to plate$\alpha $ $\;\dfrac{{ - Q}}{{2S{\varepsilon _0}}}$ (towards left)

Electric field at O due to plate β    $\dfrac{{ + {q_1}}}{{2S{\varepsilon _0}}}$ (towards right)

Electric field at O due to plate $\gamma  = \dfrac{{ - {q_2}}}{{2S{\varepsilon _0}}}$  (towards left)  $\because Q > q$

As the resultant electric field at O will be 0 so,

$E = \dfrac{{ - {q_2}}}{{2S{\varepsilon _0}}} + \dfrac{{ - Q}}{{2S{\varepsilon _0}}} + \dfrac{{ + {q_1}}}{{2S{\varepsilon _0}}}$$ = 0$

$Q = {q_1} - {q_2}$

According to law of conservation of charges there will be no loss of charges after collision,

$ + Q + q = {q_1} + {q_2}$

Subtracting both the equation

$q = 2{q_2}$

Or  ${q_2} = \dfrac{q}{2}$

So, charge on plate γ after collision ${q_2} = \dfrac{q}{2}$  unit.

Charge on plate β $ = Q + {q_2} - \dfrac{q}{2}$

(c) Find the velocity of the plate γ after the collision and at a distance d from the plate β.

Ans: After the collision the charge gets distributed among γ and β, because of this the plates start to repel each other and as the plate γ is only free to move so it will move towards its initial position. Let the velocity of plate γ after the collision at distance d be v and mass of plate be m, then gain in kinetic energy when moving from  P to B and B to P will be equal to the work done by the electric field. After collision, the electric field on plate γ at O, due to plate $\alpha $ and β.

=$\dfrac{{Q + \dfrac{q}{2}}}{{2S{\varepsilon _0}}} + \dfrac{{( - Q)}}{{2S{\varepsilon _0}}}$

${E_2}=\dfrac{\dfrac{q}{2}}{{2S{\varepsilon _0}}}$  towards right

Electric field on plate γ just before collision due to plate, $\alpha $ and β

${E_1} = \dfrac{q}{{2S{\varepsilon _0}}} + \dfrac{{( - Q)}}{{2S{\varepsilon _0}}}$

${E_1} = \dfrac{{( - Q + q)}}{{2S{\varepsilon _0}}}$

Force on plate γ just before collision =${E_1}Q$

${F_1} = \dfrac{{( - Q + q)( - Q)}}{{2S{\varepsilon _0}}} = \dfrac{{(Q - q)Q}}{{2S{\varepsilon _0}}}$

${F_2} = {E_2}\dfrac{q}{2} = \dfrac{{{{\left( {\dfrac{q}{2}} \right)}^2}}}{{2{\varepsilon _0}S}}$

$W = ({F_1} + {F_2})d$

$W = \left[ {\dfrac{{(Q - q)Q}}{{2S{\varepsilon _0}}} + \dfrac{{{{\left( {\dfrac{q}{2}} \right)}^2}}}{{2{\varepsilon _0}S}}} \right]d = \left[ {\dfrac{{{Q^2} - qQ + \dfrac{{{q^2}}}{4}}}{{2{\varepsilon _0}S}}} \right]d$

$W = \left[ \dfrac{Q^{2}-2qQ+\left(\dfrac{q}{2}\right)^{2}}{2\epsilon_0S}\right]$$\times d$

$W = \dfrac{{{{\left( {Q - \dfrac{q}{2}} \right)}^2}d}}{{2{\varepsilon _0}S}} = KE$

$\dfrac{1}{2}m{v^2} = \dfrac{{{{\left( {Q - \dfrac{q}{2}} \right)}^2}d}}{{2{\varepsilon _0}S}} = {v^2} = \dfrac{{{{\left( {Q - \dfrac{q}{2}} \right)}^2}2d}}{{2{\varepsilon _0}Sm}}$

${v^{}} = \left( {Q - \dfrac{q}{2}} \right)\sqrt {\dfrac{{^{}d}}{{{\varepsilon _0}Sm}}} $ is the velocity of plate γ at a distance d after the collision.

1.29 There is another useful system of units, besides the SI/mks. A system called the cgs (centimetre-gram-second) system. In this system Coulomb’s law is given by  $F = \dfrac{{Qq}}{{{r^2}}}\mathop r\limits^ \wedge  $where the distance r is measured in cm (= 10–2m), F in dynes (=10–5N) and the charges in electrostatic units (es units), where 1es unit of charge$ = \dfrac{1}{{\left[ 3 \right]}} \times {10^{ - 9}}C$. The number [3] actually arises from the speed of light in Vacuum which is now taken to be exactly given by c = 2.99792458 × 108m/s. An approximate value of c then is c = [3] × 108 m/s. (i) Show that the Coulomb law in cgs units yields 1 esu of charge = 1 (dyne)1/2 cm. Obtain the dimensions of units of charge in terms of mass M, length L and time T. Show that it is given in terms of fractional powers of M and L. 

Ans: $F = \dfrac{{Qq}}{{{r^2}}}\mathop r\limits^ \wedge  $

1 dyne =$\dfrac{{{{\left[ {lesu} \right]}^2}}}{{{{\left( {1cm} \right)}^2}}}$

1e.s. u=cm$\sqrt {dyne} $

1e.s.u =$L^{1}F^{\dfrac{1}{2}}=L^{1}[MLT^{-2}]^{\dfrac{1}{2}}$

1e.s. u=$M^{\dfrac{1}{2}}L^{\dfrac{3}{2}}T^{-1}$

So the dimension of 1e.s. u is $\dfrac{1}{2}$ of M,$\dfrac{3}{2}$ of L and (-1) of T.

(ii) Write 1 esu of charge = x C, where x is a dimensionless number. Show that this gives $\dfrac{1}{{4\pi \varepsilon _0^{}}} = \dfrac{{{{10}^{ - 9}}}}{{{x^2}}}\dfrac{{N{m^2}}}{{{C^2}}}$ with $ x = \dfrac{1}{{\left[ 3 \right]}} \times {10^{ - 9}} $. We have $\dfrac{1}{{4\pi \varepsilon _0^{}}} = {\left[ 3 \right]^2} \times {10^9}\dfrac{{N{m^2}}}{{{C^2}}}$ Or $\dfrac{1}{{4\pi \varepsilon _0^{}}} = {\left[ {2.99792458} \right]^2} \times {10^9}\dfrac{{N{m^2}}}{{{C^2}}}$(exactly)

Ans: 1 e.s.u = $\chi $ C[Given]

Where, $\chi $ is a dimensionless number. The  two  charges each of magnitude 1 e.s.u separated by 1 cm will have coulombic force one dyne =${10^{ - 5}}N$ which is equivalent to two charges of magnitude $\chi $C separated by ${10^{ - 2}}m$. By Coulomb’s law

$F = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{q_1}{q_2}}}{{{r^2}}}$

${q_1} = {q_2} = \chi C$

$r = 1cm = {10^2}m$

If $F=1\,dyne$,

from I,$\dfrac{1}{{4\pi {\varepsilon _0}}} = \dfrac{{1\,dyne{{(1cm)}^2}}}{{\chi \chi }} = \dfrac{{{{10}^{ - 5}}N({{10}^{ - 2}}{m^2})}}{{{\chi ^2}{C^2}}}$

$\dfrac{1}{{4\pi {\varepsilon _0}}} = \dfrac{{{{10}^{ - 9}}}}{{{\chi ^2}}}\dfrac{{N - {m^2}}}{{{C^2}}}$

$\chi  = \dfrac{1}{{3 \times {{10}^9}}}  \\ \dfrac{1}{{4\pi {\varepsilon _0}}} = {10^{ - 9}} \times {\left[ 3 \right]^2}{\left( {{{10}^9}} \right)^2}\dfrac{{N - {m^2}}}{{{C^2}}}  \\ \dfrac{1}{{4\pi {\varepsilon _0}}} = 9 \times {10^9}\dfrac{{N - {m^2}}}{{{C^2}}}  \\ $

$\dfrac{1}{{4\pi {\varepsilon _0}}} = 9 \times {10^9}N - {m^2}{C^{ - 2}}$

1.30 Two charges –each are fixed separated by distance 2d. A third charge q of

mass m placed at the mid-point is displaced slightly by x (x<<<d) perpendicular to the line joining the two fixed charges as shown in Fig. 1.14. Show that q will perform simple harmonic oscillation of time period.

$T = {\left[ {\dfrac{{8\pi {\varepsilon _ \circ }m{a^3}}}{{{q^2}}}} \right]^{\dfrac{1}{2}}}$

                            Fig 1.14

Ans: Force acting on charge q due to -q at A will be ${F_{PA}}$ along P to A.

${F_{PA}} = \dfrac{1}{{4\pi {\varepsilon _0}}}.\dfrac{{{q_1}{q_2}}}{{{r^2}}} = \dfrac{1}{{4\pi {\varepsilon _0}}}.\dfrac{{q( - q)}}{{{r^2}}}  \\ {F_{PA}} = \dfrac{{ - {q^2}}}{{4\pi {\varepsilon _ \circ }{r^2}}}  \\ {F_{PB}} = \dfrac{{ - {q^2}}}{{4\pi {\varepsilon _ \circ }{r^2}}}\left[ {\because |{F_{PA}}| = |{F_{PB}}| = F} \right]  \\ $

So, the horizontal components of FPA and FPB are equal and opposite so neutralise

Each other. The vertical components of FPA and FPB are downward and so add up.

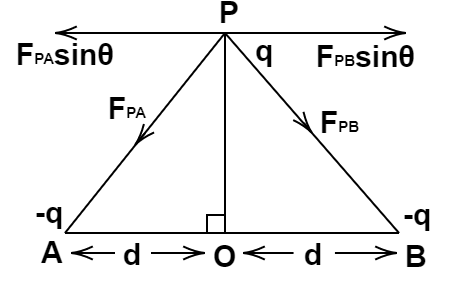
Net force on q at $P = {F_{PA}}\cos \theta  + 2F\cos \theta [\because |{F_{PA}}| = |{F_{PB}}| = F]$

$ = \dfrac{{ - 2{q^2}}}{{4\pi {\varepsilon _ \circ }{r^2}}}\cos \theta $

Force on q downwards = $\dfrac{{ - 2{q^2}}}{{4\pi {\varepsilon _ \circ }{r^2}}}.\dfrac{x}{r}$

${r^2} = {x^2} + {d^2}$ by Pythagoras theorem

$\therefore $ Force on $q = \dfrac{{ - 2{q^2}}}{{4\pi {\varepsilon _ \circ }}}.\dfrac{x}{{{{\left( {{x^2} + {d^2}} \right)}^{\dfrac{3}{2}}}}}$

$x<<<{d}$

$\therefore {x_{2}}<<< {d_{2}}$

As a negative sign shows force of attraction.

So net force on q at P downwards = $\left( {\dfrac{{ - 2{q^2}}}{{4\pi {\varepsilon _ \circ }{d^3}}}} \right)x$

So the force on q is directly proportional to the displacement from mean position O ( the midpoint of the segment joining –q and –q charges). So the motion of q about O will be S.H.M.

$F = kx$ where, $k = \dfrac{{2{q^2}}}{{4\pi {\varepsilon _ \circ }{d^3}}}$

$\therefore \omega  = \sqrt {\dfrac{k}{m}}   \\ T = \dfrac{{2\pi }}{\omega } = 2\pi \sqrt {\dfrac{m}{k}}   \\ T = 2\pi \sqrt {\dfrac{m}{{\dfrac{{2{q^2}}}{{4\pi {\varepsilon _ \circ }{d^3}}}}}}  = 2\pi \sqrt {\dfrac{{4\pi m{\varepsilon _ \circ }{d^3}}}{{2{q^2}}}}   \\ T = \left[ {\dfrac{{8\pi {\varepsilon _ \circ }m{a^3}}}{{{q^2}}}} \right]  \\$

Hence proved.

1.31 Total charge –Q is uniformly spread along the length of a ring of radius R. A small test charge +q of mass m is kept at the centre of the ring and is given a gentle push along the axis of the ring.

(a) Show that the particle executes a simple harmonic oscillation.

Ans: When the -Q charge is equally distributed along a conducting ring, the centre of ring O will be symmetric to the charge distribution. so the electric field at O will be zero. Hence force on q will be zero. Now as we displace the charge q is displaced by a small distance then about the centre O or mean position the electric field on q will not be zero so force acts on fig.

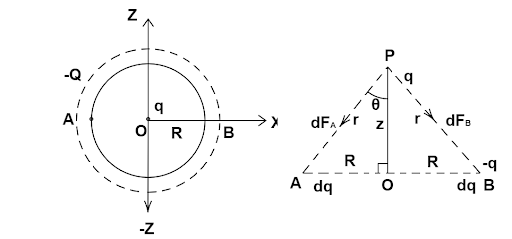
Force on q at P when z is small 

$F = {F_A} + {F_B}$

${F_y}={F_A}\cos\theta+{F_B}\cos\theta$.............(downward)

The horizontal component of FA and FB will be equal and opposite, so cancelled out.

So, the total force acting on q due to a small element dl of ring = $dF\cos \theta $

$d{F_y} = \dfrac{1}{{4\pi {\varepsilon _0}}}.\dfrac{{qdq}}{{{r^2}}}.\dfrac{z}{r}$ ($\cos \theta  = \dfrac{z}{r}$)

Charge on any small element $dl$ of ring 

$dq = \lambda dl$

$dq = \dfrac{{ - Q}}{{2\pi r}}dl$

$\therefore d{F_y} = \dfrac{{qz}}{{4\pi {\varepsilon _0}{r^3}}}.\dfrac{{\left( { - Q} \right)dl}}{{2\pi R}}$

$dF = \dfrac{{ - Qqzdl}}{{4\pi {\varepsilon _ \circ }.2\pi R{r^3}}} \\ $

Integrating both sides we get,

$\int {d{F_y}= \int\limits_0^{2\pi r} {\dfrac{{ - qQzdl}}{{4\pi {\varepsilon _ \circ }2\pi R{r^3}}}} } $

$\int {d{F_y}}  = \int\limits_0^{2\pi r} {\dfrac{{ - qQzdl}}{{4\pi {\varepsilon _0}\left( {2\pi R{r^3}} \right)}}} $

${F_y} = \dfrac{{ - qQz}}{{4\pi {\varepsilon _0}\left( {2\pi R} \right){{\left( {\sqrt {{R^2} + {z^2}} } \right)}^3}}}\int\limits_0^{2\pi r} {dl} $

Since, $r = \sqrt {{R^2} + {z^2}} $ . So, if $z <  <  < R$, ${z^2} <  <  < {R^2}$. Hence, ${z^2}$ can be neglected.

${F_y} = \dfrac{{ - qQz}}{{4\pi {\varepsilon _0}\left( {2\pi {R^4}} \right)}}\left( {2\pi R - 0} \right)$

${F_y} = \dfrac{{ - qQz}}{{4\pi {\varepsilon _0}{R^3}}}$

So, ${F_y} \propto z$

Hence, q executes SHM. 

$F =  - k{z^2}...\left[ {II} \right]$

(b) Obtain its time period.

Ans: $\therefore k = \dfrac{{Qq}}{{4\pi {\varepsilon _ \circ }{R^3}}}$............[on comparing I & II]

$\therefore T = 2 \ne \sqrt {\dfrac{m}{k}}   \\ T = 2\pi \sqrt {\dfrac{{4\pi {\varepsilon _ \circ }{R^3}}}{{Qq}}}   \\ $

Benefits of solving NCERT Exemplar Class 12 Physics Chapter 1 solutions

Students can also find NCERT intext, activities, and problems at the end of each chapter. Working on NCERT Solutions would also be extremely beneficial to students in completing their Homework and Assignments on time. Students may also download NCERT Solutions for Class 12 Physics Chapter 1 Electric Charges And Fields in PDF format. Therefore, they can access them even when they are not connected to the internet.

They can also build a strong conceptual foundation regarding this chapter and can answer questions accordingly. By studying the solutions provided by the subject matter experts, students can easily understand how a question should be answered following the CBSE guidelines and score more in the exams.

Why wait then? Clarify all your doubts about this chapter in NCERT Exemplar Physics Class 12 right away by downloading this file from Vedantu. Store it in PDF format and access it at your convenience. Complete your study material for Class 12 Physics by choosing the respective solution files for other chapters and prepare well for the board exams and competitive exams ahead.