NCERT Exemplar for Class 12 Physics - Communication Systems - Free PDF Download

Exercise

MULTIPLE CHOICE QUESTIONS-I

15.1 Three waves A, B and C of frequencies 1600 kHz, 5 MHz and 60 MHz, respectively are to be transmitted from one place to another. Which of the following is the most appropriate mode of communication:

(a) A is transmitted via space wave while B and C are transmitted via sky wave.

(b) A is transmitted via ground wave, B via sky wave and C via space wave.

(c) B and C are transmitted via ground wave while A is transmitted via sky wave.

(d) B is transmitted via ground wave while A and C are transmitted via space wave.

Ans: Option (b)

Since the range of frequencies for the ground wave propagation is 530KHz to 1710 kHz, sky wave propagation is 1710 kHz to 40 MHz, and space wave propagation is 54 MHz to 42 GHz, therefore the given waves must be transmitted by ground, sky and space waves respectively.Hence, the correct answer is (b).

15.2 A 100m long antenna is mounted on a 500m tall building. The complex can become a transmission tower for waves with λ

(a) ~400m.

(b) ~25m.

(c) ~150m.

(d) ~2400m.

Ans: Option (d)

The height of a given antenna from the ground level of earth can be given by the sum of heights of the building and the antenna. That gives us,

$ \Rightarrow l = 100 + 500$

i.e.

$ \Rightarrow l = 600m$

Now the wavelength of the wave transmitted by the antenna will be given by the formula,

$ \Rightarrow \lambda  = 4l$

That gives us,

$ \Rightarrow \lambda  = 4 \times 600$

i.e.

$ \Rightarrow \lambda  = 2400m$

Hence, the correct answer is (d).

15.3 A 1 KW signal is transmitted using a communication channel which provides attenuation at the rate of – 2dB per km. If the communication channel has a total length of 5 km, the power of the signal received is $\left[ {{\text{gain in }}dB = 10\log \left( {\dfrac{{{P_0}}}{{{P_i}}}} \right)} \right]$ .

(a) 900 W.

(b) 100 W.

(c) 990 W.

(d) 1010 W.

Ans: Option (b)

Given that, ${P_i} = 1kW = 1000W$

Rate of attenuation of signal is $ - 2dB/km$ .

Length of the communication channel is $5km$ .

Hence the gain in attenuation will be $ - 2\left( 5 \right) =  - 10$ 

But it is given that,

$ \Rightarrow {\text{gain in }}dB = 10\log \left( {\dfrac{{{P_0}}}{{{P_i}}}} \right)$

Hence, we have

$ \Rightarrow  - 10 = 10\log \left( {\dfrac{{{P_0}}}{{1000}}} \right)$

That gives,

$ \Rightarrow  - 1 = \log \left( {\dfrac{{{P_0}}}{{1000}}} \right)$

That is,

$ \Rightarrow \log 10 =  - \log \left( {\dfrac{{{P_0}}}{{1000}}} \right)$

Or,

$ \Rightarrow \log 10 = \log \left( {\dfrac{{1000}}{{{P_0}}}} \right)$

Hence,

$ \Rightarrow 10 = \dfrac{{1000}}{{{P_0}}}$

i.e.

$ \Rightarrow {P_0} = 100W$

Hence, the correct answer is (b).

15.4 A speech signal of 3 kHz is used to modulate a carrier signal of frequency 1 MHz, using amplitude modulation. The frequencies of the side bands will be

(a) 1.003 MHz and 0.997 MHz

(b) 3001 kHz and 2997 kHz.

(c) 1003 kHz and 1000 kHz.

(d) 1 MHz and 0.997 MHz.

Ans: Option (a)

Since we have, ${\omega _c} = 1MHz = {10^6}Hz$

And the frequency of the message signal is given as ${\omega _m} = 3kHz = 3000Hz$

Therefore, the frequencies of the side bands will be given by $\left( {{\omega _c} + {\omega _m}} \right)$ and $\left( {{\omega _c} - {\omega _m}} \right)$ respectively.

That is,

$ \Rightarrow \left( {{\omega _c} + {\omega _m}} \right) = {10^6} + 3000 = 1003000Hz$

And

$ \Rightarrow \left( {{\omega _c} - {\omega _m}} \right) = {10^6} - 3000 = 997000Hz$

Hence, the correct answer is (a).

15.5 A message signal of frequency ${\omega _m}$ is superposed on a carrier wave of frequency ${\omega _c}$ to get an amplitude modulated wave (AM). The frequency of the AM wave will be

(a) ${\omega _m}$

(b) ${\omega _c}$

(c) $\dfrac{{{\omega _c} + {\omega _m}}}{2}$

(d) $\dfrac{{{\omega _c} - {\omega _m}}}{2}$

Ans: Option (b)

The frequency of the amplitude modulated wave is the same as that of the carrier wave. Hence, the correct answer is (b).

15.6 I-V characteristics of four devices are shown in Fig. 15.1

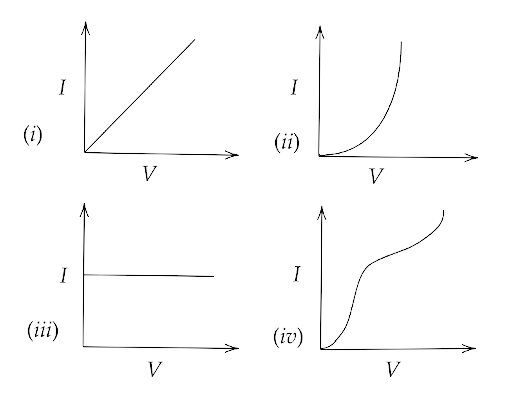
Identify devices that can be used for modulation:

(a) ‘i’ and ‘iii’.

(b) only ‘iii’.

(c) ‘ii’ and some regions of ‘iv’.

(d) All the devices can be used.

Ans: Option (c)

The devices which follow the square law are used for modulation. The graphs shown in (i) and (iii) are linear. Only the graph (ii) and some regions of graph (iv) follow the square law. Hence, the correct answer is (c).

15.7 A male voice after modulation-transmission sounds like that of a female to the receiver. The problem is due to

(a) poor selection of modulation index (selected 0 < m < 1)

(b) poor bandwidth selection of amplifiers.

(c) poor selection of carrier frequency

(d) loss of energy in transmission

Ans: Option (b)

This is happening because the frequency of the modulated signal is more than the input signal. This is possibly due to the poor bandwidth selection of the amplifiers. Hence, the correct answer is (b).

15.8 A basic communication system consists of

(A) transmitter.

(B) information source.

(C) user of information.

(D) channel.

(E) receiver.

Choose the correct sequence in which these are arranged in a basic communication system:

(a) ABCDE.

(b) BADEC.

(c) BDACE.

(d) BEADC.

Ans: Option (b)

The correct sequence in which these are arranged in a basic communication system is BADEC. In a  communication system, the information is transmitted to a channel which is then received by the user. Hence, the correct answer is (b).

15.9 Identify the mathematical expression for amplitude modulated wave:

(a) ${A_c}{\text{sin}}\left[ {\left\{ {{\omega _c} + {k_1}{v_m}\left( t \right)} \right\}t + \phi } \right]$

(b) ${A_c}{\text{sin}}\left\{ {{\omega _c}t + \phi  + {k_2}{v_m}\left( t \right)} \right\}$

(c) $\left\{ {{A_c} + {k_2}{v_m}\left( t \right)} \right\}{\text{sin}}\left( {{\omega _c}t + \phi } \right)$

(d) ${A_c}{v_m}\left( t \right){\text{sin}}\left( {{\omega _c}t + \phi } \right)$

Ans: Option (c)

Let the signal which is to be modulated be $m\left( t \right) = {A_m}\sin {\omega _m}t$ where ${A_m}$ is the amplitude of the modulated signal.

Then,

$ \Rightarrow {A_m} = {{\rm A}_c} + m\left( t \right)$

Hence,

$ \Rightarrow {A_m} = {{\rm A}_c} + {A_m}\sin {\omega _m}t$

Or,

$ \Rightarrow {A_m} = {{\rm A}_c}\left[ {1 + \dfrac{{{A_m}}}{{{{\rm A}_c}}}\sin {\omega _m}t} \right]$

That is,

$ \Rightarrow {A_m} = {{\rm A}_c} + \mu {{\rm A}_c}\sin {\omega _m}t$

Now since, ${C_m}\left( t \right) = {{\rm A}_m}\sin {\omega _c}t$

Therefore,

$ \Rightarrow {C_m}\left( t \right) = \left( {{{\rm A}_c} + \mu {{\rm A}_c}\sin {\omega _m}t} \right)\sin {\omega _c}t$

Now let $\mu {A_c} = {k_2}$ and $\sin {\omega _m}t = {v_m}\left( t \right)$

Then we can write,

$ \Rightarrow {C_m}\left( t \right) = \left( {{{\rm A}_c} + {k_2}{v_m}\left( t \right)} \right)\sin \left( {{\omega _c}t + \phi } \right)$

Hence, the correct answer is (c).

MULTIPLE CHOICE QUESTIONS-II

MORE THAN ONE OPTION

15.10 An audio signal of 15 kHz frequency cannot be transmitted over long distances without modulation because

(a) the size of the required antenna would be at least 5 km which is not convenient.

(b) the audio signal cannot be transmitted through sky waves.

(c) the size of the required antenna would be at least 20 km, which is not convenient.

(d) effective power transmitted would be very low, if the size of the antenna is less than 5 km.

Ans: Options (a), (b) and (d)

Here, the frequency of the audio signal is given as ${v_m} = 15kHz = 15 \times {10^3}Hz$

Hence, the wavelength of this signal is ${\lambda _m} = \dfrac{c}{{{v_m}}} = \dfrac{{3 \times {{10}^8}}}{{15 \times {{10}^3}}} = 0.2 \times {10^5}m$

Therefore, the size of antenna will be $h = \dfrac{\lambda }{4} = \dfrac{{20000}}{4} = 5000m = 5km$

Since the audio waves have very less frequencies, hence they can not be transmitted through sky waves otherwise they’ll be absorbed by the atmosphere. If the height of the antenna is below 5km then the effective power transmission would be very low due to the deviation from resonance of the wavelength of the signal and it’s antenna length. Hence, the correct answer is (a), (b) and (d).

15.11 Audio sine waves of 3 kHz frequency are used to amplitude modulate a carrier signal of 1.5 MHz. Which of the following statements are true?

(a) The side band frequencies are 1506 kHz and 1494 kHz.

(b) The bandwidth required for amplitude modulation is 6kHz.

(c) The bandwidth required for amplitude modulation is 3 MHz.

(d) The side band frequencies are 1503 kHz and 1497 kHz.

Ans: Options (b) and (d)

Given that, ${\omega _m} = 3kHz$ and ${\omega _c} = 1.5MHz = 1500kHz$

Hence the frequency of the side bands will be $1500 \pm 3kHz$

i.e. $1497kHz$ and $1503kHz$

Also the bandwidth of the signal is $2{\omega _m} = 6kHz$

Hence, the correct answer is (b) and (d).

15.12 A TV transmission tower has a height of 240 m. Signals broadcast from this tower will be received by LOS communication at a distance of (assume the radius of earth to be 6.4 × 106 m)

(a) 100 km.

(b) 24 km.

(c) 55 km.

(d) 50 km.

Ans: Options (b), (c) and (d)

Given that $h = 240m$ and $R = 6.4 \times {10^6}m$

Now the range of this signal is,

$ \Rightarrow d = \sqrt {2Rh} $

That is,

$ \Rightarrow d = \sqrt {2 \times 6.4 \times {{10}^6} \times 240} $

Or,

$ \Rightarrow d = 8 \times 1{0^3} \times 4\sqrt 3 $

Hence,

$ \Rightarrow d = 32000 \times 1.732$

I.e.

$ \Rightarrow d = 55424m$

Since the range of the signal is 55.424km, hence it will be received at a distance of 24km, 55km and 50km. Hence, the correct answer is (b), (c) and (d).

15.13 The frequency response curve (Fig. 15.2) for the filter circuit used for production of AM wave should be

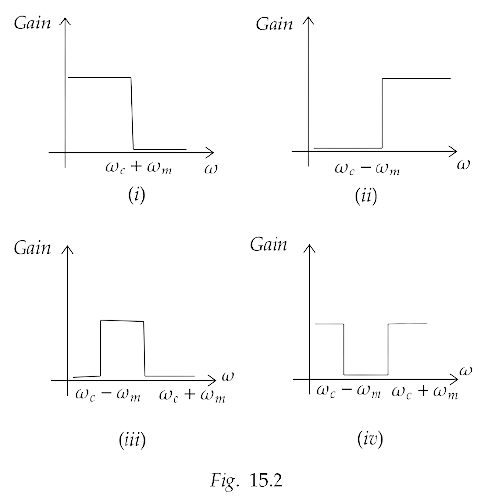
(a) (i) followed by(ii).

(b) (ii) followed by(i).

(c) (iii).

(d) (iv).

Ans: Options (a), (b) and (c)

The unwanted frequencies of the signal are cut off by the band pass filter. The frequency response of a circuit is the variation in its behaviour with changes in the input signal frequency as it shows the band of frequencies over which the output and the gain remains fairly constant. Hence, the correct answer is (a), (b) and (c).

15.14 In amplitude modulation, the modulation index m, is kept less than or equal to 1 because

(a) m > 1, will result in interference between carrier frequency and message frequency, resulting in distortion.

(b) m > 1 will result in overlapping of both side bands resulting into loss of information.

(c) m > 1 will result in change in phase between carrier signal and message signal.

(d) m > 1 indicates amplitude of message signal greater than amplitude of carrier signal resulting in distortion.

Ans: Options (b) and (d)

Since the modulation index m or $\mu $ is given by $\mu  = \dfrac{{{A_m}}}{{{A_c}}}$

Hence, we have

$ \Rightarrow \mu  = \dfrac{{\Delta {v_{\max }}}}{{{v_{m\left( {\max } \right)}}}} = \dfrac{{{\text{Frequency deviation}}}}{{{\text{Maximum frequency of modulated wave}}}}$

Now if we have $m > 1$ then it implies that $\Delta {v_{\max }} > {v_{m\left( {\max } \right)}}$ . So it will cause overlapping of both sidebands of the modulated wave which results in a loss of information. Hence, the correct answer is (b) and (d).

VERY SHORT ANSWER TYPE QUESTIONS

15.15 Which of the following would produce analogue signals and which would produce digital signals?

(i) A vibrating tuning fork.

(ii) Musical sound due to a vibrating sitar string.

(iii) Light pulse.

(iv) Output of NAND gate.

Ans: (i) A vibrating fork and the (ii) musical sound due to a vibrating sitar string will produce analogue signals whereas (iii) light pulse and (iv) output of NAND gate will produce digital signals.

15.16 Would sky waves be suitable for transmission of TV signals of 60 MHz frequency?

Ans: Sky waves are used to transmit a signal of frequency ranging between 1710 kHz to 40 MHz. The frequency of 60 MHz is beyond the range of sky waves. Hence, sky waves won’t be suitable for transmission but space waves can be used.

15.17 Two waves A and B of frequencies 2 MHz and 3 MHz, respectively, are beamed in the same direction for communication via sky waves. Which one of these is likely to travel a longer distance in the ionosphere before suffering total internal reflection?

Ans: Given that, the frequency of wave B is more than wave A which is directly proportional to their refractive indices, hence the refractive index of wave B is also greater than wave A.

Now, since refractive index is inversely proportional to the critical angle therefore it means that the critical angle of wave A is greater than wave B. Hence, it implies that wave B is more likely to travel a longer distance in the ionosphere before suffering the total internal reflection.

15.18 The maximum amplitude of an A.M. the wave is found to be 15 V while its minimum amplitude is found to be 3 V. What is the modulation index?

Ans: Given that, ${A_{\max }} = {A_c} + {A_m} = 15V$ and ${A_{\min }} = {A_c} - {A_m} = 3V$

Hence, ${A_c} = 9V$ and ${A_m} = 6V$

Now, modulation index will be given by,

$ \Rightarrow \mu  = \dfrac{{{A_m}}}{{{A_c}}} = \dfrac{6}{9} = \dfrac{2}{3} = 0.\overline 6 $

15.19 Compute the LC product of a tuned amplifier circuit required to generate a carrier wave of 1 MHz for amplitude modulation.

Ans: Given frequency is $v = 1MHz = {10^6}Hz$

Now since we know that,

$ \Rightarrow v = \dfrac{1}{{2\pi \sqrt {LC} }}$

Or,

$ \Rightarrow \sqrt {LC}  = \dfrac{1}{{2\pi v}}$

Hence,

$ \Rightarrow LC = \dfrac{1}{{4{\pi ^2}{v^2}}}$

That gives us,

$ \Rightarrow LC = \dfrac{{{{10}^{ - 12}}}}{{4{\pi ^2}}}$

i.e.

$ \Rightarrow LC = 2.54 \times {10^{ - 14}}{\sec ^2}$

15.20 Why is an AM signal likely to be more noisy than a FM signal upon transmission through a channel?

Ans: Due to the variation of the instantaneous voltage in an amplitude modulated wave, noise can be received considering it a part of the modulated signal. Moreover, The frequency of the carrier wave fluctuates as the amplitude of the modulating signal varies in frequency modulated carrier waves. As a result, the receiver does not presume noise in the FM signal.

SHORT ANSWER TYPE QUESTIONS

15.21 Figure 15.3 shows a communication system. What is the output power when the input signal is 1.01mW? $\left( {{\text{gain in }}dB = 10{{\log }_{10}}\left( {\dfrac{{{P_0}}}{{{P_i}}}} \right)} \right)$

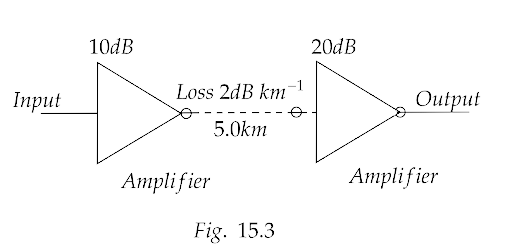
Ans: Since the loss of signal is given as 2dB per km,

Hence, total loss in 5km is $5 \times \left( { - 2} \right) =  - 10dB$

Total gain in signal in input and output amplifier is $10 + 20 = 30dB$

Hence overall output signal gained is $30 - 10 = 20dB$

Now since $\left( {{\text{gain in }}dB = 10{{\log }_{10}}\left( {\dfrac{{{P_0}}}{{{P_i}}}} \right)} \right)$

Therefore,

$ \Rightarrow 20 = 10{\log _{10}}\left( {\dfrac{{{P_0}}}{{{P_i}}}} \right)$

$ \Rightarrow 2 = {\log _{10}}\left( {\dfrac{{{P_0}}}{{{P_i}}}} \right)$

That is,

$ \Rightarrow \log {10^2} = {\log _{10}}\left( {\dfrac{{{P_0}}}{{{P_i}}}} \right)$

Hence,

$ \Rightarrow 100 = \dfrac{{{P_0}}}{{{P_i}}}$

That gives,

$ \Rightarrow {P_0} = 100 \times {P_i}$

Hence,

$ \Rightarrow {P_0} = 100 \times 1.01mW$

i.e.

$ \Rightarrow {P_0} = 101mW$

15.22 A TV transmission tower antenna is at a height of 20 m. How much service area can it cover if the receiving antenna is

(i) at ground level,

Ans: Given that, ${h_T} = 20m$ and $R = 6.4 \times {10^6}m$

(i) Range of transmission 

$ \Rightarrow {r_1} = \sqrt {2{h_T}R} $

That gives,

$ \Rightarrow {r_1} = \sqrt {2 \times 20 \times 6.4 \times {{10}^6}m} $

$ \Rightarrow {r_1} = 16000m$

Area covered is $\pi {r_1}^2 = 803.84\,k{m^2}$

(ii) at a height of 25 m? Calculate the percentage increase in area covered in case (ii) relative to case (i).

Ans: Range of transmission

$ \Rightarrow {r_2} = \sqrt {2{h_T}R}  + \sqrt {2{h_R}R} $

That gives us,

$ \Rightarrow {r_2} = \sqrt {2 \times 20 \times 6.4 \times {{10}^6}m}  + \sqrt {2 \times 25 \times 6.4 \times {{10}^6}m} $

Hence,

$ \Rightarrow {r_2} = 16000m + 4000\sqrt {20} $

i.e.

$ \Rightarrow {r_2} = 33.9km$

Area covered is $\pi {r_2}^2 = 3608.52\,k{m^2}$

Percentage increase in area is $\dfrac{{3608.52 - 803.84}}{{803.84}} \times 100 = \dfrac{{280400}}{{803.84}} = 3848.9\% $

15.23 If the whole earth is to be connected by LOS communication using space waves (no restriction of antenna size or tower height), what is the minimum number of antennas required? Calculate the tower height of these antennas in terms of earth's radius?

Ans: Let us consider the minimum number of antennas that are required to connect the earth by LOS communication. Now if we consider 1 or 2 antennas then it would be insufficient to cover the whole earth as shown in the figure below.

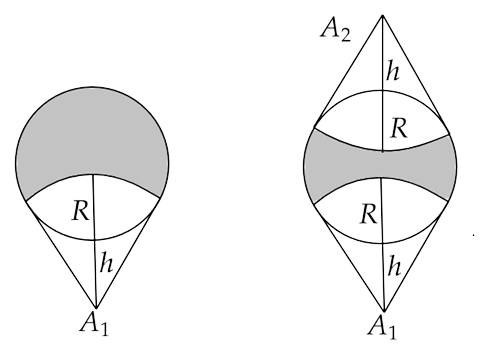
Similarly, 3 or 4 antennas will also leave a shaded region that is out of the reach of LOS communication.

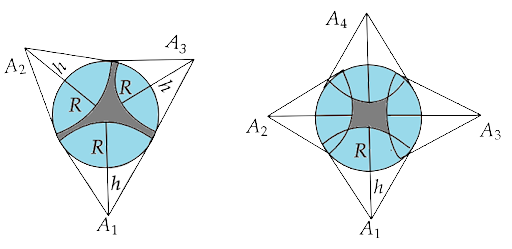
Now, if we consider 5 antennas, then it can cover the first half of the earth but it will still leave a small region on the other side that is unreachable by the LOS communication.

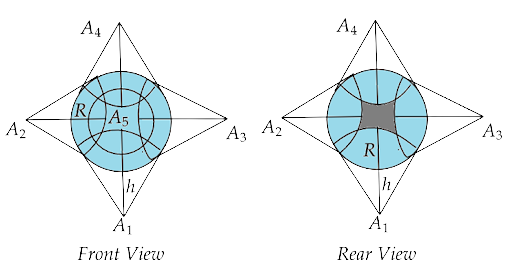
Now, from the figure we can say that only one more antenna is needed to cover the shaded region.

Now, if we consider six transmitters or towers at six equivalent positions (A, B, C, D, O and O’) on the surface of earth as represented in the figure below.

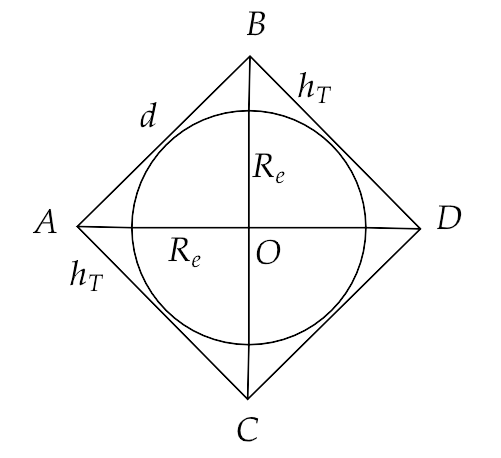
Here, the heights of transmitter and receiver towers are equal, i.e. ${h_T} = {h_R}$

Therefore, if we consider the range of signal to be $d$ then we have,

$ \Rightarrow d = \sqrt {2{h_T}{R_e}}  + \sqrt {2{h_R}{R_e}} $

i.e.

$ \Rightarrow d = \sqrt {2{h_T}{R_e}}  + \sqrt {2{h_T}{R_e}} $

Hence,

$ \Rightarrow d = 2\sqrt {2{h_T}{R_e}} $ ...(1)

Also in the triangle AOB, we have

$ \Rightarrow {d^2} = {\left( {{h_T} + {R_e}} \right)^2} + {\left( {{h_T} + {R_e}} \right)^2}$

That gives us,

$ \Rightarrow {d^2} = 2{\left( {{h_T} + {R_e}} \right)^2}$

i.e.

$ \Rightarrow d = \left( {{h_T} + {R_e}} \right)\sqrt 2 $ ...(2)

Now from equation (1) and (2), we have

$ \Rightarrow 2\sqrt {2{h_T}{R_e}}  = \left( {{h_T} + {R_e}} \right)\sqrt 2 $

Squaring both sides, gives us

$ \Rightarrow 8{h_T}{R_e} = 2{\left( {{h_T} + {R_e}} \right)^2}$

$ \Rightarrow 4{h_T}{R_e} = \left( {{h_T}^2 + {R_e}^2 + 2{h_T}{R_e}} \right)$

That can be written as,

$ \Rightarrow {h_T}^2 + {R_e}^2 - 2{h_T}{R_e} = 0$

Hence,

$ \Rightarrow {\left( {{h_T} - {R_e}} \right)^2} = 0$

That gives us,

$ \Rightarrow {h_T} = {R_e}$

Therefore, the minimum number of antennas required is six and the height of each tower of these antennas is equal to the radius of earth.

15.24 The maximum frequency for reflection of sky waves from a certain layer of the ionosphere is found to be ${f_{\max }} = 9{\left( {{N_{\max }}} \right)^{\dfrac{1}{2}}}$ , where ${N_{\max }}$ is the maximum electron density at that layer of the ionosphere. On a certain day it is observed that signals of frequencies higher than 5MHz are not received by reflection from the ${F_1}$ layer of the ionosphere while signals of frequencies higher than 8MHz are not received by reflection from the ${F_2}$ layer of the ionosphere. Estimate the maximum electron densities of the ${F_1}$ and ${F_2}$ layers on that day.

Ans: For layer ${F_1}$ , we have

$ \Rightarrow {F_{\max }} = 5 \times {10^6}Hz$

Hence,

$ \Rightarrow {N_{\max }} = \dfrac{{{{\left( {{F_{\max }}} \right)}^2}}}{{9 \times 9}}$

That gives,

$ \Rightarrow {N_{\max }} = \dfrac{{25 \times {{10}^{12}}}}{{9 \times 9}}$

$ \Rightarrow {N_{\max }} = 3.086 \times {10^{11}}e/{m^3}$

For layer ${F_2}$ , we have

$ \Rightarrow {F_{\max }} = 8 \times {10^6}Hz$

Similarly,

$ \Rightarrow {N_{\max }} = \dfrac{{{{\left( {{F_{\max }}} \right)}^2}}}{{9 \times 9}}$

$ \Rightarrow {N_{\max }} = \dfrac{{8 \times 8 \times {{10}^{12}}}}{{9 \times 9}}$

i.e.

$ \Rightarrow {N_{\max }} = 7.9 \times {10^{11}}e/{m^3}$

15.25 On radiating (sending out) an AM modulated signal, the total radiated power is due to energy carried by ${\omega _c}$ , ${\omega _c} - {\omega _m}$ & ${\omega _c} + {\omega _m}$ . Suggest ways to minimize the cost of radiation without compromising on information.

Ans: In amplitude modulated signal, only the side bands frequencies carry the information, hence sending either ${\omega _c} - {\omega _m}$ or ${\omega _c} + {\omega _m}$ or both can reduce the cost of radiation of information signals.

LONG ANSWER TYPE QUESTIONS

15.26 The intensity of a light pulse travelling along a communication channel decreases exponentially with distance x according to the relation $I = {I_0}{e^{ - \alpha x}}$ , where ${I_0}$ is the intensity at x = 0 and α is the attenuation constant.

(i)Show that the intensity reduces by 75 per cent after a distance of $\left( {\log \dfrac{4}{\alpha }} \right)$ .

Ans: Given that, $I = {I_0}{e^{ - \alpha x}}$

Also, the intensity reduces by 75% i.e. to 25%

That is, 25% of ${I_0}$ i.e. $\dfrac{{{I_0}}}{4}$ 

Now we have,

$ \Rightarrow \dfrac{{{I_0}}}{4} = {I_0}{e^{ - \alpha x}}$

$ \Rightarrow \dfrac{1}{4} = {e^{ - \alpha x}}$

That is,

$ \Rightarrow x = \dfrac{{\log 4}}{\alpha }$

Hence the intensity reduces by 75% at a distance $x = \dfrac{{\log 4}}{\alpha }$ .

(ii) Attenuation of a signal can be expressed in decibel (dB) according to the relation $dB = 10{\log _{10}}\left( {\dfrac{I}{{{I_0}}}} \right)$ . What is the attenuation in dB/km for an optical fibre in which the intensity falls by 50 per cent over a distance of 50 km?

Ans: Let the attenuation of the signal be $\beta $ .

Then we have,

$ \Rightarrow 10{\log _{10}}\left( {\dfrac{I}{{{I_0}}}} \right) =  - \beta x$

Also $x = 50km$ and $I = \dfrac{{{I_0}}}{4}$

Hence,

$ \Rightarrow 10{\log _{10}}\left( {\dfrac{1}{2}} \right) =  - 50\beta $

That is,

$ \Rightarrow \beta  = \dfrac{{10}}{{50}}{\log _{10}}2$

i.e.

$ \Rightarrow \beta  = \dfrac{{10}}{{50}} \times 0.3010$

$ \Rightarrow \beta  = 0.0602dB$

15.27 A 50 MHz sky wave takes 4.04 ms to reach a receiver via re-transmission from a satellite 600 km above earth’s surface. Assuming re-transmission time by satellite is negligible, find the distance between source and receiver. If communication between the two was to be done by Line of Sight (LOS) method, what should the size and placement of the receiving and transmitting antenna be?

Ans: Let the transmitter be at a position T and the receiver be at position R.

Let S be a satellite at a distance 600km from a point E on earth.

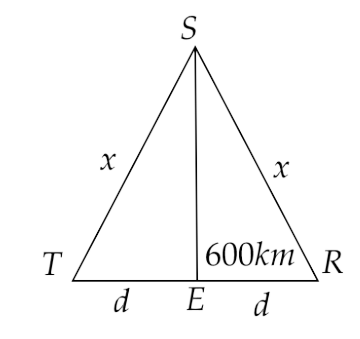
Let $TE = ER = d$ and $ST = SR = x$

By echo-method, we have $t = 4.04 \times {10^{ - 3}}s$

Therefore,

$ \Rightarrow x = \dfrac{{vt}}{2} = \dfrac{{3 \times {{10}^8} \times 4.04 \times {{10}^{ - 3}}}}{2} = 6.06 \times 1{0^5}m = 606km$

Using Pythagoras theorem, we have

$ \Rightarrow d = \sqrt {{{606}^2} - {{600}^2}} $

That is,

$ \Rightarrow d = 85.06km$

Now,

$ \Rightarrow TR = 2d = 170.12km$

For maximum distance,

$ \Rightarrow d = \sqrt {2R{h_T}}  = \sqrt {2 \times 6.4 \times {{10}^3} \times {h_T}}  = \sqrt {7236} $

That gives,

$ \Rightarrow {h_T} = \dfrac{{7236}}{{2 \times 6.4 \times {{10}^3}}}$

$ \Rightarrow {h_T} = 566m$

Hence, the height required for the antenna is 566 m.

15.28 An amplitude modulated wave is as shown in Fig. 15.4. Calculate

(i) the percentage modulation,

Ans: From the figure, the maximum and minimum voltage is given as 50 and 10 Volts respectively.

(i) The percentage modulation is $\dfrac{{50 - 10}}{{50 + 10}} \times 100\%  = \dfrac{{40}}{{60}} \times 100\%  = 66.67\% $

(ii) peak carrier voltage 

Ans: The peak carrier voltage is $\dfrac{{50 + 10}}{2} = \dfrac{{60}}{2} = 30V$

(iii) peak value of information voltage.

Ans: The peak value of information voltage is $66.67\%  \times 30V = \dfrac{{66.67}}{{100}} \times 30V = 20V$

15.29 (i) Draw the plot of amplitude versus ‘ω’ for an amplitude modulated wave whose carrier wave ( ${\omega _c}$ ) is carrying two modulating signals, ${\omega _1}$ and ${\omega _2}$ (${\omega _2} > {\omega _1}$  ).

Ans: The plot of amplitude versus ‘ω’ for an amplitude modulated wave whose carrier wave ( ${\omega _c}$ ) is carrying two modulating signals, ${\omega _1}$ and ${\omega _2}$ (${\omega _2} > {\omega _1}$  ) is shown below.

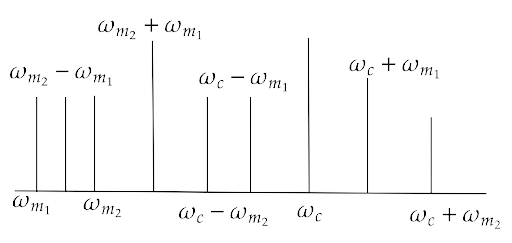
(ii) Is the plot symmetrical about ${\omega _c}$ ? Comment especially about plot in region $\omega  < \omega c$ .

Ans: No, the plot is not symmetrical about ${\omega _c}$ as many frequencies lie below and before ${\omega _c}$ .

(iii) Extrapolate and predict the problems one can expect if more waves are to be modulated.

Ans: There will be more frequency lines in the region less than which makes overlapping i.e. noise of signals if more waves are modulated.

(iv) Suggest solutions to the above problem. In the process can one understand another advantage of modulation in terms of bandwidth?

Ans: The frequency of ${\omega _c}$ as well as the bandwidth must be increased in order to accumulate more modulated signals i.e. information.

15.30 An audio signal is modulated by a carrier wave of 20MHz such that the bandwidth required for modulation is 3kHz. Could this wave be demodulated by a diode detector which has the values of R and C as

(i) R = 1 kΩ, C = 0.01μF.

Ans: Given that, ${f_c} = 20 \times {10^6}Hz$

Hence, ${\omega _c} = 2\pi {f_c} = 2\pi  \times 20 \times {10^6} = 40\pi  \times {10^6}rad/s$

Bandwidth, $2{f_m} = 3 \times {10^3}Hz$

That gives ${f_m} = 1.5 \times {10^3}Hz$

Now, demodulation by diode is possible if and only if we have the condition $\dfrac{1}{{{f_c}}} <  < RC < \dfrac{1}{f}$ satisfied.

Here, $\dfrac{1}{{{f_c}}} = \dfrac{1}{{20 \times {{10}^6}}} = 5 \times {10^{ - 8}}/Hz$

And, $\dfrac{1}{{{f_m}}} = \dfrac{1}{{1.5 \times {{10}^3}}} = 0.7 \times {10^{ - 3}}/Hz$

(i) Here $RC = 1000 \times 0.01 \times {10^{ - 6}} = {10^{ - 5}}$

Therefore, from the above condition, we have $5 \times {10^{ - 8}} <  < {10^{ - 5}} < 0.7 \times {10^{ - 3}}$ satisfied.

Hence, this wave can be demodulated.

(ii) R = 10 kΩ, C = 0.01μF.

Ans: Here, $RC = 10000 \times 0.01 \times {10^{ - 6}} = {10^{ - 4}}$

Therefore, from the above condition, we have $5 \times {10^{ - 8}} <  < {10^{ - 4}} < 0.7 \times {10^{ - 3}}$ satisfied.

Hence, this wave can be demodulated.

(iii) R = 10 kΩ, C = 0.1μF

Ans: Here, $RC = 10000 \times 0.1 \times {10^{ - 6}} = {10^{ - 8}}$

Therefore, from the above condition, we have $5 \times {10^{ - 8}} > {10^{ - 8}} < 0.7 \times {10^{ - 3}}$ 

Hence, this wave cannot be demodulated.

How Exactly Does It Happen Free PDF

How exactly does this happen? It is in the way that concepts like Amplitude, Frequency, Range, Phase, Amplification and Bandwidth are utilized in setting up Communication Systems. Don’t we use this system frequently, “I am not getting rang here!” or “My system does not have that bandwidth.” These are Examples of how we use Physics  in our day-to-day language and living. 

When you study the practical uses of a subject like Physics , it opens up your mind to new dimensions and levels of perception. You don’t view it as a theoretical subject anymore! The NCERT Exemplar Solutions helps you enhance this worldview by offering guided solutions to the most challenging Exercises in a student-friendly manner.