Thermodynamics Class 11 Notes CBSE Physics Chapter 11 (Free PDF Download)

Section-A (1 Mark Questions)

1. What is an ideal gas? Give its main characteristics.

Ans. An ideal gas is one which obeys the gas laws at all values of temperature and pressure. Its main characteristics are (i) The size of the molecules is negligibly small. (ii) There is no force of attraction or repulsion amongst its molecules.

2. Why do the gases at low temperature and high pressure show large deviations from ideal behavior?

Ans. At low temperature and high pressure. the intermolecular attractions become appreciable. Moreover, the volume occupied by the gas molecules cannot be neglected in compariAnsn to the volume of  the gas. Hence the real gases show large deviations from deal gas behaviour.

3. When an automobile travels for a long distance, the air pressure in the tyres increases slightly. Why?

Ans. Due to the friction between the tyres and the road, the tyres get heated. The temperature of air inside the tyres increases. Consequently, the air pressure in the tyres increases slightly.

4. What a gas is heated, its temperature increases. Explain it on the basis of kinetic theory of gases.

Ans. When a gas is heated, the root mean square velocity of its molecules increases. As $V_{rms}\varpropto\sqrt{T}$ , Ans the temperature of the gas increases.

5. Given a sample of 1 cm3 of hydrogen and 1 cm3 of oxygen both at S.T.P. Which sample has a larger number of molecules?

Ans. Both the samples contain the same number of molecules in accordance with Avogadro’s law.

6. Although the velocity of air molecules is nearly 0.5 kms-1, yet the smell of scent spreads at a much slower rate. Why?

Ans. The air molecules travel along a zig-zag path due to frequent collisions. As a result, their displacement per unit time is very small. Hence the smell of scent spreads very slowly.

7. State the law of equi-partition of energy.

Ans. According to law of equi partition of energy, the average kinetic energy of a molecule in each degree of freedom is same and is equal to $\dfrac{1}{2}KT$

8. What is a cyclic process? What is the change in internal energy of a system after it completes one cycle of such a process? 

Ans. Any process in which the system returns to its initial state after undergoing a series of changes is known as a cyclic process. The change in internal energy after complete cycle is zero because the system returns to its initial state.

9. When is the heat supplied to a system equal to the increase in its internal energy?

Ans. According to the first law of thermodynamics, $\Delta Q=\Delta U+P\Delta V$ . If the heat is supplied in such a manner that the volume does not change (for iAnschoric change, $\Delta V=0$ ). Then whole of the heat energy supplied to the system will increase, internal energy only.

10. When a gas in suddenly compressed, its temperature rises. Why? 

Ans. Sudden compression of a gas is an adiabatic process. The work done in compressing the gas increases ‘the internal energy of the gas. Hence the temperature of the gas rises.

Section-B (2 Marks Questions)

11. What are the limitations of first law of thermodynamics?

Ans. The limitations are

(i) There is no information about the direction in which change takes place.  

(ii) lt does not give any idea about the extent to which the change takes place

12. In a Carnot engine, the temperature of the sink is increased. What will happen to its efficiency? 

Ans. Efficiency, $\eta =1-\dfrac{T_{2}}{T_{1}}$ . If the temperature $\left ( T_{2} \right )$ of the sink is increased, the efficiency of the Carnot engine will decrease.

13. A sample of an ideal gas occupies a volume V at a pressure P and abAnsute temperature T. The mass of each molecule is m. If KB is the Boltzmann’s constant, then write the expression for the density of the gas.

Ans. According to kinetic theory of gases, $P=\dfrac{1}{3}\rho \bar{v}^{2}=\dfrac{2}{3}\dfrac{\rho }{m}\cdot \dfrac{1}{2}m\bar{v}^{2}=\dfrac{2}{3}\cdot \dfrac{\rho }{m}\cdot \dfrac{3}{2}k_{B}T$ 

∴ Density $\rho =\dfrac{P}{k_{B}T}$ .

14. Write the equation of state of 16g of O2.

Ans. Number of moles in 32g of O2 =1

∴ Number of moles in 16 g of $O_{2}=\dfrac{1}{32}\times 16=\dfrac{1}{2}$ 

As PV = nRT and $n=\dfrac{1}{2}$ Ans $PV=\dfrac{1}{2}RT$

15. A gas in a closed vessel is at the pressure P0. If the masses of all the molecules be made half and their speeds be made double, then find the resultant pressure.

Ans. $P_{0}=\dfrac{1}{3}\dfrac{mN}{V}v^{2}$

$\therefore {P}'=\dfrac{1}{3}\dfrac{m/2}{V}\left ( 2v \right )^{2}=\dfrac{2}{3}\dfrac{mN}{V}v^{2}=2P_{0}$

16. Find out the ratio between most probable velocity, average velocity and root Mean square Velocity of gas molecules?

Ans. Since,

Most Probable velocity, $v_{mp}=\sqrt{\dfrac{2KT}{m}}$ 

Average velocity, $\bar{v}=\sqrt{\dfrac{8KT}{\pi m}}$ 

Root Mean Square velocity; $v_{rms}=\sqrt{\dfrac{3KT}{m}}$ 

So, $v_{mp}:\bar{v}:v_{rms}=\sqrt{\dfrac{2KT}{m}}:\sqrt{\dfrac{3KT}{\pi m}}:\sqrt{\dfrac{3KT}{m}}$ 

$=\sqrt{2}:\sqrt{\dfrac{8}{\pi }}:\sqrt{3}$ 

PDF Summary - Class 11 Physics Thermodynamics Notes (Chapter 11)

1. THERMODYNAMICS 

It deals with the study of interactions between heat and other forms of energy.

Thermodynamic System: 

A collection of large numbers of molecules of matter (solid, liquid or gas) that are arranged in a manner such that these possess particular values of pressure, volume and temperature forms a thermodynamic system.

The parameters like pressure, volume, temperature, internal energy, etc., which determine the state or condition of a system are termed thermodynamic state variables.

In thermodynamics, we consider the thermodynamic systems as a whole and learn the interaction of heat and energy during the change of one thermodynamic state to another.

1.1 Thermal Equilibrium

The term ‘equilibrium’ in thermodynamics refers to the state when all the macroscopic variables expressing the system (\[P,\text{ }V,\text{ }T\] , mass etc.,) do not change with time. 

• Two systems when in contact with each other are said to be in thermal equilibrium when their temperatures become the same. 

• Zeroth law of thermodynamics states that when the thermodynamics systems A and B are separately in thermal equilibrium with a third thermodynamic system C, then the systems A and B are also in thermal equilibrium with each other.

1.2 Heat, Work and Internal Energy 

Internal Energy refers to the energy possessed by any system because of its molecular kinetic energy and molecular potential energy. Both these energies are considered with respect to the center of mass frame.

Internal energy is dependent entirely on the state and thus, it is a state variable. In the case of real gases, internal energy is only by virtue of their molecular motion whereas for ideal gases, it is mathematically given by

$U=\frac{nfRT}{2}$

where,

$n$ is the number of moles

$f$ is the degree of freedom

$R$ is the universal gas constant

$T$ is the temperature in kelvin

Internal Energy can be altered either by providing heat energy or by performing some work.

Heat Energy refers to the energy transformed to or from the system due to the difference in temperatures by conduction, convection or radiation.

The energy that gets transferred from one system to another by force moving its point of application in its own direction is termed work.

Mathematically, work done by the system is given by

\[W=\int{Fdx}=\int{{{P}_{s}}}Adx=\int{PdV}\]

where ${{P}_{s}}$ is the pressure of the system on the piston. 

This work done by the system is positive when the system is expanding and it is negative when the system is contracting. 

• Work and heat are path functions while internal energy is a state function. 

• Heat and work are two different terminologies even though they might look similar.

1.3 Important Thermodynamics Terms 

State Variables: \[P,\text{ }V,\text{ }T,\text{ moles}\]

State variables can be extensive or intensive.

Equation of State: The equation that relates the pressure $(P)$, the volume $(V)$ and absolute temperature $(T)$ of a gas is known as the equation of state. 

\[PV=\text{constant}\] (Boyle’s Law) 

\[\frac{V}{T}=constant\] (Charles’ Law) 

\[\Rightarrow PV=nRT\]

Thermodynamic Process: A thermodynamic process happens when a few changes occur in the state of a thermodynamic system, i.e., the thermodynamic parameters of the system get altered with time. Thermodynamic process can be isothermal, adiabatic, isobaric or isochoric. 

Quasi Static Process: A thermodynamic process that is infinitely slow is termed quasi-static process. 

• In a quasi static process, the system undergoes change with slow speed such that at every instant, the system is in both thermal and mechanical equilibrium with the surroundings.

• Quasi-static process is an ideal process. We generally consider all the processes to be quasi static unless mentioned differently.

Indicator P-V Diagram: A graph between pressure and volume of a gas under thermodynamic operation is known as a P-V diagram.

With respect to the diagram;

\[a\text{ }\to \text{ Isobaric }\] (Constant Pressure)

\[b\text{ }\to \text{ Isothermal }\] (Constant Temperature)

\[c\text{ }\to \text{Adiabatic }\] (Q= Constant)

\[d\text{ }\to \text{Isochoric}\] (Constant Volume)

Also, the area under the P-V diagram provides us the work done by a gas.

1.4 First Law of Thermodynamics

Suppose that

\[\Delta Q=\] Heat supplied to the system by the surroundings 

\[\Delta W=\] Work done by the system on the surroundings 

\[\Delta U=\] Change in internal energy of the system. 

First law of thermodynamics suggests that energy can neither be created nor be destroyed. It can only be transformed from one form to another. Thus, first law of thermodynamics states that the total amount of heat supplied to the system by the surroundings will be equal to the sum of the Work done by the system on the surroundings and the change in internal energy of the system. 

Mathematically, 

\[\Delta Q=\Delta U+\Delta W\]

Sign Conventions: 

• When heat gets supplied to the system, then \[\Delta Q\] is taken positive and when heat gets withdrawn from the system, \[\Delta Q\] is taken negative. 

• When a gas expands, work done by the gas is taken positive whereas when a gas contracts, work is taken negative.

• \[\Delta U\]is taken positive when temperature increases while \[\Delta U\] is taken negative when temperature decreases.

It is to be noted here that we always take work done by the system. In chemistry, work done on the system is considered. Hence there is another perspective to the first law of thermodynamics in chemistry. Mathematically, this can be expressed as

\[\Delta Q - \Delta W=\Delta U\] 

where \[\Delta Q\] and \[\Delta U\] have the same meanings but $W$ stands for the work done on the system.

1.5 Application of the First of Law of Thermodynamics 

Here, we observe how the first law of thermodynamics is applied to different thermodynamic processes.

1.5.1 Isothermal Process 

Description: A thermodynamic process in which the temperature remains constant.

Condition: The walls of the container should be perfectly conductive to allow free exchange of heat between the gas and its surroundings. 

The process of compression or expansion must be slow in order to provide time for exchange of heat. 

Both these conditions are considered perfectly ideal. 

Equation of State: $T=$ Constant or ${{P} {v}}=$ Constant 

Indicator Diagram:

Slope of $P-V$ at any point is equal to $-\frac{P}{V}$. 

Change in internal energy, \[\Delta U=0\]  (Temperature remains constant)

Work done is given by

$W=\int\limits_{{{v}_{1}}}^{{{v}_{2}}}{{{P}_{g}}dV}$ 

$\Rightarrow W=\int\limits_{{{v}_{1}}}^{{{v}_{2}}}{\left( \frac{nRT}{V} \right)}dV$  [Using $PV=nRT$]

$\Rightarrow W=nRT\ln \left( \frac{{{v}_{2}}}{{{v}_{1}}} \right)$

First Law of Thermodynamics:

$Q=\Delta U+W$ 

$\Rightarrow Q=nRT\ln \left( \frac{{{v}_{2}}}{{{v}_{1}}} \right)$ 

Remarks: All the heat supplied is utilized entirely to do work against external surroundings. When heat is supplied, then the gas expands whereas when heat is withdrawn, then the gas contracts.

Practical Examples: 

Melting of ice at \[0{}^\circ C\]. 

Boiling of ${{H}_{2}}O$ at \[100{}^\circ C\].

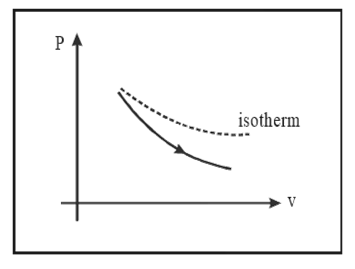
1.5.2 Adiabatic Process

Description: A thermodynamic process in which there is no heat exchange with surroundings.

Conditions: The walls of the container should be perfectly non-conducting in order to prevent any exchange of heat between the gas and its surroundings. 

The process of compression or expansion must be rapid so that there is no time for the exchange of heat. 

These conditions are ideal conditions and are difficult to achieve.

Equation of State:

\[P{{V}^{r}}=\text{constant}\] 

$\Rightarrow T{{V}^{r-1}}=\text{constant}$ 

$\Rightarrow P{{T}^{\frac{r}{1-r}}}=\text{constant}$ 

Indicator Diagram

Slope of adiabatic curve $=-r\frac{P}{V}$ 

As given in the graph, the adiabatic curve is steeper than the isothermal curve. Change in internal energy, $\Delta U=\frac{nfR\Delta T}{2}=\frac{nR\left( {{T}_{2}}-{{T}_{1}} \right)}{r-1}=\frac{{{P}_{2}}{{V}_{2}}-{{P}_{1}}{{V}_{1}}}{r-1}$. 

Work done by the gas when it adiabatically expands from ${{V}_{1}}\text{ to }{{V}_{2}}$  is given by

$W=\int\limits_{{{v}_{1}}}^{{{v}_{2}}}{\frac{dV}{{{V}^{r}}}}$ 

$\Rightarrow W=\text{constant}\int\limits_{{{v}_{1}}}^{{{v}_{2}}}{\frac{dV}{{{V}^{r}}}}$ 

$\because P{{V}^{r}}=\text{constant}$

$\Rightarrow P=\frac{\text{constant}}{{{V}^{r}}}$

\[\Rightarrow W=\text{constant}\times \left[ \frac{{{V}^{-r+1}}}{1-r} \right]_{{{v}_{1}}}^{{{v}_{2}}}\] 

$\Rightarrow W=\frac{\text{constant}}{1-r}\left[ \frac{1}{V_{2}^{r-1}}-\frac{1}{V_{1}^{r-1}} \right]$ 

Also, it is known that

${{P}_{1}}V_{1}^{r}={{P}_{2}}V_{2}^{r}=\text{constant}$ 

\[\Rightarrow W=\frac{1}{1-r}\left[ \frac{{{P}_{2}}{{V}_{2}}}{V_{2}^{r-1}}-\frac{{{P}_{1}}{{V}_{1}}}{V_{1}^{r-1}} \right]\] 

$\Rightarrow W=\frac{{{P}_{2}}{{V}_{2}}-{{P}_{1}}{{V}_{1}}}{1-r}=\frac{nR\left( {{T}_{1}}-{{T}_{2}} \right)}{r-1}$

First Law of Thermodynamics

\[Q=\Delta U+W\] 

Substituting the values 

We get \[Q=0\], as expected 

Remarks: When gas expands adiabatically, then its temp decreases and vice versa.

Practical Examples:

Propagation of sound waves in the form of compression and rarefaction. 

Spontaneous bursting of a cycle tube.

1.5.3 Isochoric Process 

Description: A thermodynamic process in which the volume remains constant.

Condition: A gas being heated or cooled inside a rigid container.

Equation of State: \[V=\text{constant or }\frac{P}{T}=\text{constant}\] 

Indicator Diagram:

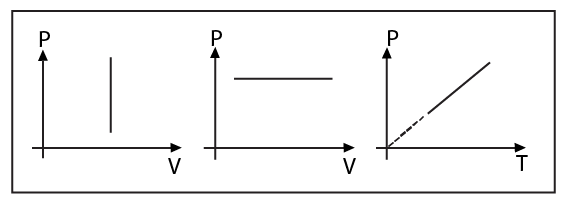
Change in internal energy is given by

$\Delta U=\frac{nfR\Delta T}{2}=\frac{nR\left( {{T}_{2}}-{{T}_{1}} \right)}{r-1}$ 

$\Rightarrow \Delta U=\frac{{{P}_{2}}{{V}_{2}}-{{P}_{1}}{{V}_{1}}}{r-1}=\frac{nR\Delta T}{r-1}$

Work done is given by $W=0$ since the gas does not expand.

First Law of thermodynamics 

\[Q=\Delta U+W\] 

\[\Rightarrow Q\text{ }=\frac{nfR\Delta T}{2}\] 

Remarks: As we have learnt that when heat is supplied to any process, its temperature increases according to relation:

$Q=nC\Delta T$ 

$\Rightarrow C=\frac{Q}{n\Delta T}$ 

Now, this $C$ is dependent on external conditions for gases. 

Here, it is referred to as ${{\left. \frac{\Delta Q}{n\Delta T} \right|}_{v}}$i.e., Molar heat capacity at constant volume. 

Mathematically, it can be derived as 

\[{{C}_{v}}=\frac{\text{ }fR}{2}\]

1.5.4 Isobaric Process 

Description: A thermodynamic process in which the pressure remains constant. 

Condition: When in a container, the piston can move freely and it is not connected by any agent.

Equation of State: 

\[P=\text{constant}\] or \[\frac{V}{T}=\text{constant}\]

Indicator Diagram:

(Image Will Be Updated Soon)

Change in internal energy, $\Delta U=\frac{nfR\Delta T}{2}$  is the same as always. 

Work done is given by

$W=\int{PdV}=P\Delta V$ 

(since pressure is constant)

$\Rightarrow W=P{{V}_{2}}-PV=nR\Delta T$

First Law of Thermodynamics 

\[Q=\Delta U+W\] 

\[\Rightarrow Q\text{ }=\frac{nfR\Delta T}{2}\text{ +}nR\Delta T\]

$\Rightarrow Q=\left[ \frac{fR}{2}+R \right]\Delta T$ 

Remarks: Just like ${{C}_{V}}$, we may define molar heat capacity at constant pressure as ${{C}_{P}}={{\left. \frac{Q}{n\Delta T} \right|}_{P}}$. 

Mathematically, it can be derived as:

${{C}_{P}}=\frac{fR}{2}+R$ 

Replacing $\frac{fR}{2}$ by ${{C}_{V}}$, we get \[{{C}_{P}}+{{C}_{V}}=R\], which known as Mayer’s Relation.

Notes:

• Just like molar specific heat at constant pressure and molar specific heat at constant volume, we may define molar specific heat for any process. 

For example: 

\[{{C}_{\text{adiabatic}}}=0\] 

\[{{C}_{\text{isothermal}}}=\infty \] 

Basically, gases do not possess unique specific heats though we have \[{{C}_{P}}\text{ and }{{C}_{V}}\] mainly.

Specific Heat at Constant Volume: It refers to the amount of heat needed to raise the temperature of $1g$ of a gas through $1{}^\circ C$, when its volume is kept constant. It is denoted by \[{{c}_{V}}\].

Specific Heat at Constant Pressure: It refers to the amount of heat needed to raise the temperature of $1g$ of a gas through $1{}^\circ C$ keeping its pressure constant. It is denoted by ${{c}_{P}}$.

• Here, it is to be noted that \[{{C}_{P}},{{C}_{V}}\] refer to molar heat capacity while \[{{c}_{P}},\text{ }{{\text{c}}_{V}}\] refer to specific heat capacity. 

• \[{{C}_{V}}=M{{c}_{V}}\text{ and }{{C}_{P\text{ }}}=M{{c}_{P}}\] where $M$ stands for molar mass of any sample.

$\Rightarrow {{c}_{P}}-{{c}_{V}}=\frac{{{C}_{P}}-{{C}_{V}}}{M}=\frac{R}{M}$

1.5.5 Melting Process 

In any case, the first law is always applicable. 

During the melting process,

Internal energy, \[Q=m{{L}_{f}}\] , as studied earlier and where \[{{L}_{f}}\] is the latent heat of fusion.

Work done, \[W=0\]. 

(In the change of state from solid to liquid, we do not consider any expansion or contraction as it is very small) 

With respect to the first law of thermodynamics, 

$\Delta U=Q-W$

$\Rightarrow \Delta U=m{{L}_{f}}$

Remark: The heat provided during melting is utilized in increasing the internal energy of any substance.

1.5.6 Boiling Process 

During the boiling process, 

Internal energy, \[Q=m{{L}_{V}}\], where \[{{L}_{V}}\] is the latent heat of vaporization.  

Work done, \[W=P\left[ {{V}_{2}}{{V}_{1}} \right]\]. 

(Pressure is constant during boiling and it is equal to atmospheric pressure) 

With respect to the first law of thermodynamics, 

$\Delta U=Q-W$ 

$\Rightarrow \Delta U=m{{L}_{f}}-P\left( {{V}_{2}}-{{V}_{1}} \right)$

1.5.7 Cyclic Process

A cyclic process refers to the process wherein the system returns to its initial stage after undergoing a series of change.

Example Indicator Diagram

Here, change in internal energy, $\Delta U=m{{L}_{V}}=0$. 

Work done, $W=$ Area under the loop. 

$\Rightarrow Q=W$ according to the first law of thermodynamics. 

Also, $W$ is positive when the cycle is clockwise whereas it is negative when the cyclic is anti-clockwise.

1.6 Limitations of the First Law of Thermodynamics 

• The first law does not provide the direction in which the change can occur. 

• The first law provides no idea on the extent of change.

• The first law of thermodynamics provides no information about the source of heat. i.e., whether it is a hot or a cold body.

1.7 Heat Engines 

Heat engine is a device which converts heat energy into mechanical energy.

Key Elements 

• A source of heat at higher temperature 

• A working substance 

• A sink of heat at lower temperature

Working

• The working substance follows a cycle consisting of several processes. 

• In some processes, it absorbs a total amount of heat \[{{Q}_{1}}\] from the source at temperature ${{T}_{1}}$. 

• In some other processes, it rejects a total amount of heat \[{{Q}_{2}}\] to the sink at a lower temperature \[{{T}_{2}}\]. 

• The work done by the system in a cycle gets transferred to the environment with the help of an arrangement.

Schematic Diagram

First Law of Thermodynamics

Since energy is always conserved, 

${{Q}_{1}}=W+{{Q}_{2}}$

Thermal Efficiency of a heat engine refers to the ratio of net work done per cycle by the engine to the total amount of heat absorbed per cycle by the working substance from the source. It is represented by $\eta $. Mathematically,

$\eta =\frac{W}{{{Q}_{1}}}$ 

Substituting for ${{Q}_{1}}$, we get 

$\Rightarrow \eta =1-\frac{{{Q}_{2}}}{{{Q}_{1}}}$ 

Ideally, engines must have efficiency $\eta =1$.

Remarks: The mechanism of conversion of heat into work varies for various heat engines: 

• The system which gets heated by an external furnace similar to a steam engine. These engines are called external combustion engines.

• The system wherein heat is produced by burning the fuel inside the main body of the engine. These engines are called internal combustion engines.

1.8 Refrigerator and Heat Pumps 

A refrigerator or heat pump is a device utilized for cooling things. 

Key Elements 

• A cold reservoir at temperature ${{T}_{2}}$ 

• A working substance 

• A hot reservoir at temperature ${{T}_{1}}$ 

Working 

• The working substance follows a cycle consisting of several processes. 

• A sudden expansion of the gas from high to low pressure cools it and converts it into a vapor-liquid mixture. 

• Absorption by the cold fluid of heat from the region to be cooled converts it into vapor. 

• The vapor gets heated up due to external work done on the working substance. 

• The heat gets released by the vapor to the surroundings bringing it to the initial state and completing the cycle.

Schematic Diagram

First Law of Thermodynamics 

\[{{Q}_{2}}+W={{Q}_{1}}\] 

Coefficient of performance of refrigerator $(\beta )$ refers to the ratio of quantity of heat removed per cycle from contents of the refrigerator $\left( {{Q}_{2}} \right)$ to the energy spent per cycle $(W)$ to remove this heat. Mathematically, 

$\beta =\frac{{{Q}_{2}}}{W}$  

Substituting for $W$, we get 

$\Rightarrow \beta =\frac{{{Q}_{2}}}{{{Q}_{1}}-{{Q}_{2}}}$ 

Ideally, heat pumps must have $\beta =\infty $.

1.9 Second Law of Thermodynamics 

There are a lot of ways in which this law can be stated.

Even though all the statements are the same with respect to their contents, the following two are the most significant. 

Kelvin Planck Statement: No process is possible whose sole result is the absorption of heat from a reservoir and the complete conversion of the heat into work. 

Clausius Statement: No process is possible whose sole result is the transfer of heat from a colder object to a hotter object. 

Significance: $100%$ efficiency in heat engines or infinite CoP in refrigerators is not possible.

1.10 Reversible and Irreversible Process 

Reversible Process: A thermodynamic process taking a system from initial state $i$ to final state $f$ is considered reversible if the process can be reversed back such that both the system and the surroundings return to their original states with no other change anywhere else in the universe. 

Conditions for reversibility: 

1. Process must proceed at an extremely slow rate, i.e., process is quasi-static so that the system is in equilibrium with surroundings at every stage. 

2. The system must be free from dissipative forces like friction, inelasticity, viscosity, etc.

Examples: No process can be considered perfectly reversible though a slow expansion of an ideal gas is approximately reversible.

Irreversible Process: A process that does not satisfy any of the conditions of a reversible process is known as an irreversible process.

Causes:

• Spontaneous process 

• Presence of friction, viscosity and other dissipative forces

Significance of Reversibility:

• Major concern of thermodynamics is the efficiency with which the heat is converted into mechanical energy. 

• Second law of thermodynamics opts out the possibility of a perfect heat engine with $100%$ efficiency. 

• It is found that heat engines based on idealized reversible processes attain the highest possible efficiency.

2.11 Carnot Engine 

Sadi Carnot devised an ideal cycle of operation for a heat engine termed the Carnot cycle. 

The engine used for realizing this ideal cycle is known as the Carnot heat engine.

Construction 

The essential sections of an ideal heat engine or Carnot heat engine are shown in the diagram below.

1. Source of heat: The source is maintained at a fixed higher temperature ${{T}_{1}}$, from which the working substance takes heat. The source is supposed to possess infinite thermal capacity and as such any amount of heat can be taken from it without altering its temperature. 

2. Sink of heat: The sink is maintained at a fixed lower temperature ${{T}_{2}}$, to which any amount of heat can be emitted by the working substance. It also has infinite thermal capacity and as such its temperature remains constant at ${{T}_{2}}$ , even when any amount of heat is emitted to it. 

3. Working substance: A perfect gas plays the role of a working substance. It is contained in a cylinder with non-conducting sides but having a perfectly conducting-base. This cylinder is fixed with a perfectly non-conducting and frictionless piston. 

Apart from these essential parts, there is also a perfectly insulating stand or pad on which the cylinder can be positioned. It provides complete isolation to the working substance from the surroundings so that the gas can undergo adiabatic changes.

Working

The Carnot cycle consists of the following four stages: 

1. Isothermal expansion 

2. Adiabatic expansion 

3. Isothermal compression 

4. Adiabatic compression

The cycle is carried out by making use of the Carnot engine as detailed below:

Consider one gram mole of an ideal gas enclosed in the cylinder. Let \[{{V}_{1}}\], \[{{P}_{1}}\] and \[{{T}_{1}}\] be the initial volume, pressure and temperature of the gas respectively. The initial state of the gas is demonstrated by point A in the above P-V diagram. We may assume that all the four processes are quasi-static and non-dissipative in nature, which are the two conditions for reversibility.

Steps 

1. Isothermal Expansion: 

The cylinder is positioned on the source and the gas is allowed to expand from $A({{V}_{1}},{{P}_{1}})$ to $B({{V}_{2}},{{P}_{2}})$ by slow outward motion of piston. As the base is perfectly conducting, the process is isothermal. 

Now, 

$\Delta {{U}_{1}}=0$; 

$\Rightarrow {{Q}_{1}}={{W}_{1}}=R{{T}_{1}}\ln \left( \frac{{{V}_{2}}}{{{V}_{1}}} \right)=Area\text{ }ABMKA$ 

where,

${{Q}_{1}}\to \text{Heat absorbed by gas}$in this process

${{W}_{1}}\to \text{Work done by gas}$ in this process

2. Adiabatic Expansion: 

The cylinder is now removed from the source and is positioned on the perfectly insulating pad. The gas is allowed to expand further from $B({{P}_{2}},{{V}_{2}})\text{ to }C({{P}_{3}},{{V}_{3}})$. As the gas is thermally insulated from all sides, the process is adiabatic. 

Here,

${{Q}_{2}}=0$;  

$\Rightarrow \Delta {{U}_{2}}={{W}_{2}}=\frac{R\left( {{T}_{2}}-{{T}_{1}} \right)}{r-1}=\text{Area BCNMB}$

3. Isothermal Compression: 

The cylinder is now removed from the insulating pad and is positioned on the sink at a temperature ${{T}_{2}}$. The piston is moved slowly so that the gas is compressed until the pressure is \[{{P}_{4}}\] and the volume is ${{V}_{4}}$.

Here,

$\Delta {{U}_{3}}=0$ 

${{W}_{3}}={{Q}_{3}}=R{{T}_{2}}\ln \left( \frac{{{V}_{4}}}{{{V}_{3}}} \right)=-\text{Area CDLNC}$

where,

${{Q}_{3}}=\text{Heat absorbed in this process}$ 

${{W}_{3}}=\text{Work done by gas in this process}$ 

4. Adiabatic Compression: 

The cylinder is again positioned on the insulating pad such that the process remains adiabatic. Here, the gas is further compressed to its initial pressure and volume. i.e., ${{P}_{1}}\text{ and }{{V}_{1}}$. 

Here,

${{Q}_{4}}=0$;

${{W}_{4}}=\Delta {{U}_{4}}=\frac{R\left( {{T}_{1}}-{{T}_{2}} \right)}{r-1}=-\text{Area DAKLD}$

Analysis:

Total work done by the engine per cycle is derived as:

\[W={{W}_{1}}+{{W}_{2}}+{{W}_{3}}+{{W}_{4}}\] 

$\Rightarrow W={{W}_{1}}+{{W}_{3}}$ 

$\Rightarrow W=R{{T}_{1}}\ln \left( \frac{{{V}_{2}}}{{{V}_{1}}} \right)+R{{T}_{2}}\ln \left( \frac{{{V}_{4}}}{{{V}_{3}}} \right)$ 

${{Q}_{1}}=\text{Total heat absorbed}=R{{T}_{1}}\ln \left( \frac{{{V}_{2}}}{{{V}_{1}}} \right)$ 

${{Q}_{2}}=\text{Total heat released}=-R{{T}_{2}}\ln \left( \frac{{{V}_{4}}}{{{V}_{3}}} \right)$

Clearly, it is seen that for a heat engine, 

$W={{Q}_{1}}-{{Q}_{2}}=\text{Area under ABCDA}$

Efficiency of Carnot Engine

Mathematically, efficiency of a Carnot engine is given by

$\eta =\frac{W}{{{Q}_{1}}}=1-\frac{{{Q}_{2}}}{{{Q}_{1}}}$

Now, considering all the adiabatic processes, we have

${{T}_{1}}V_{2}^{r-1}={{T}_{2}}V_{3}^{r-1}$ and ${{T}_{1}}V_{1}^{r-1}={{T}_{2}}V_{4}^{r-1}$

$\Rightarrow \frac{{{V}_{2}}}{{{V}_{1}}}=\frac{{{V}_{3}}}{{{V}_{4}}}$ 

Clearly,

$\Rightarrow \frac{{{Q}_{1}}}{{{Q}_{2}}}=\frac{{{T}_{1}}}{{{T}_{2}}}$

$\Rightarrow {{\eta }_{\text{Carnot}}}=1-\frac{{{T}_{2}}}{{{T}_{1}}}$

Division 

• \[{{\eta }_{\text{Carnot}}}\] is dependent only on source temperature and sink temperature. 

• \[{{\eta }_{\text{Carnot}}}=1\] only when ${{T}_{2}}=0\text{ }K\text{ or }{{T}_{1}}=\infty $, which is not possible to achieve.

• If  ${{T}_{2}}={{T}_{1}}\Rightarrow \eta =0$, heat cannot be converted to mechanical energy unless there is equal difference between the temperature of source as well as sink.

1.12 Carnot Theorem 

Statement

1. Working between two given temperatures, ${{T}_{1}}$ of hot reservoir (the source) and ${{T}_{2}}$ of cold reservoir (the sink), no engine can have efficiency more than that of the Carnot engine. 

2. The efficiency of the Carnot engine is not dependent on the nature of the working substance.

Proof

Step - 1: Consider a reversible engine R and an irreversible engine I working between the source (hot reservoir at ${{T}_{1}}$) and sink (cold reservoir at ${{T}_{2}}$). 

Step - 2: Pair up two engines in such a manner that I act like a heat engine and $R$ acts like a refrigerator. 

Step - 3: Suppose that the engine I absorbs ${{Q}_{1}}$ heat from the source; deliver a work ${{W}^{1}}$ and release the balance \[{{Q}_{1}}-{{W}^{1}}\] to the sink in a single cycle.

Step - 4: Setup $R$ such that it returns the same heat to the source, taking ${{Q}_{2}}$  from the sink and requiring a work $W={{Q}_{1}}-{{Q}_{2}}$ to be done on it. 

Step - 5: Suppose ${{\eta }_{R}}<{{\eta }_{I}}$ i.e., When $R$ were to act as an engine, it would give less work output than that of $I$.

$\Rightarrow W<{{W}^{1}}$ for a given ${{Q}_{1}}$ and $\text{ }{{Q}_{1}}-W>{{Q}_{1}}-{{W}^{1}}$

Step - 6: In totality, the I-R system extracts heat $\left( {{r}_{1}}-W \right)-\left( {{Q}_{1}}-{{W}^{1}} \right)={{W}^{1}}-W$ and delivers the same amount of work in a single cycle without any change in source or anywhere else. This contradicts the second law of thermodynamics. (Kelvin - Planck statement) 

Clearly, the assumption ${{q}_{1}}>{{q}_{R}}$ is incorrect.

A similar argument can be set up for the second statement of the Carnot theorem, i.e., Carnot efficiency is independent of the working substance. 

Thus, $\frac{{{Q}_{1}}}{{{Q}_{2}}}=\frac{{{T}_{1}}}{{{T}_{2}}}$ will always hold true for any working substance used in a Carnot engine.

2. KINETIC THEORY OF GASES 

In this topic, we would discuss the behavior of gases and how the different state variables like \[P,\text{ }V,\text{ }T,\text{ moles},\text{ }U\] are connected with each other.

2.1 Molecular Nature of Matter 

Similar to the atomic theory given by Delton, atoms are treated as the smallest constituents of elements. All the atoms of an element are identical while atoms of different elements are different. 

In solids: Atoms are tightly packed; interatomic spacing is of the order of \[\overset{o}{\mathop{A}}\,\]; interatomic force of attraction is strong. 

In liquids: Atoms are not as tightly packed as in solids; interatomic spacing is of the order of \[2\overset{o}{\mathop{A}}\,\]; interatomic force of attraction is relatively weaker.

In Gases: Atoms are free to move anywhere; interatomic spacing is of the order of \[10\overset{o}{\mathop{A}}\,\]; interatomic forces are much weaker in gases than both in solids and liquids. 

In this chapter, we would be concentrating more on gases.

2.2 Molecular Nature of Matter 

2.2.1 Ideal Gas 

Ideal gas refers to a gas that strictly obeys all the gas laws (such as Boyle’s law, Charles’ law, Gay Lussac’s law, etc.).

Characteristics 

• The size of the molecule of an ideal gas is considered to be zero.

• There would be no force of attraction or repulsion amongst the molecules of an ideal gas.

2.2.3 Ideal Gas Laws

Avogadro Hypothesis: This hypothesis suggests that Equal volumes of all gas under identical conditions of pressure and temperature would contain an equal number of molecules. 

Perfect Gas Equation: Perfect gas equation is given by

\[PV=nRT\]  

where, 

$n=$ Number of moles

$r=$ Universal Gas constant $={{N}_{A}}{{k}_{B}}$ 

${{N}_{A}}=$ Avogadro number 

${{k}_{B}}=$ Boltzmann constant 

\[R=8.314\text{ J/mol K}\]  

Boyle’s Law: When the temperature of a provided mass of gas is kept constant, its pressure varies inversely with the volume of gas. Mathematically,

\[PV=\text{constant}\] 

Charles Law: When pressure of a provided mass is kept constant, volume of the gas varies directly with the temperature of the gas. Mathematically,

\[V\propto T\] 

Dalton’s Law of Partial Pressures: The total pressure of a mixture of ideal gases is considered as the sum of partial pressures exerted by the individual gases in that mixture. Mathematically,

\[PV=\left( {{n}_{1}}+{{n}_{2}}+{{n}_{3}}+... \right)RT\] 

\[\Rightarrow P=\left( {{n}_{1}}+{{n}_{2}}+{{n}_{3}}+... \right)\frac{RT}{V}\] 

\[\Rightarrow P={{P}_{1}}+{{P}_{2}}+......\] 

where \[{{P}_{1}}=\frac{{{n}_{1}}RT}{V}\] is the partial pressure related with the gas having ${{n}_{1}}$ moles.

Deviation of Real Gas from Ideal Gas 

2.3 Kinetic Theory Postulates 

1. A gas consists of a very large number of molecules (of the order of Avogadro’s number, ${{10}^{23}}$), which are perfect elastic spheres. For a given gas, they are identical in all respects but for different gases, they are different. 

2. The molecules of a gas are in a state of incessant random motion. They move in all directions with different speeds, (of the order of $500\text{ m/s}$) and obey Newton’s laws of motion. 

3. The size of the gas molecules is very small as compared to the distance between them. If typical size of molecule is \[2\overset{o}{\mathop{A}}\,\], average distance between the molecules is \[\ge 20\overset{o}{\mathop{A}}\,\]. Thus, the volume occupied by the molecules is negligible when compared to the volume of the gas. 

4. The molecules do not exert any force of attraction or repulsion on each other except during collision. 

5. The collisions of the molecules with themselves and with the walls of the vessel are perfectly elastic. Also, that momentum and the kinetic energy of the molecules are conserved during collisions even though their individual velocities change.

6. There is no concentration of the molecules at any point inside the container i.e., molecular density is uniform throughout the gas. 

7. A molecule moves along a straight line between two successive collisions and the average straight distance covered between two successive collisions is termed the mean free path of the molecules. 

8. The collisions are almost instantaneous, i.e., the time of collision of two molecules is negligible as compared to the time interval between two successive collisions.

2.4 Pressure of an Ideal Gas and its expression 

Pressure exerted by the gas is because of continuous bombardment of gas molecules against the walls of the container. 

Expression:

Suppose that a gas is enclosed in a cube of side $1$. Consider the axes to be parallel to the sides of the cube, as shown in figure. A molecule with velocity $\left( {{v}_{x}},{{v}_{y}},{{v}_{z}} \right)$ hits the planar wall parallel to $yz-$plane of area $A\left( ={{l}^{2}} \right)$. As the collision is elastic, the molecule rebounds with the same velocity; its $y\text{ and }z$ components of velocity do not change in the collision but the x-component reverses with respect to its sign. That is, the velocity after collision is $\left( -{{v}_{x}},{{v}_{y}},{{v}_{z}} \right)$. The change in momentum of the molecule is given by $-m{{v}_{x}}-\left( m{{v}_{x}} \right)=-2m{{v}_{x}}$. Considering the principle of conservation of momentum, the momentum imparted to the wall in the collision $=2m{{v}_{x}}$. 

To calculate the force (and pressure) on the wall, we are to calculate momentum imparted to the wall per unit time, when it is within the distance ${{v}_{x}}\Delta t$ from the wall. That is, the total number of molecules within the volume $A{{v}_{x}}\Delta t$ which can hit the wall in time $\Delta T$ is $\frac{1}{2}A{{v}_{x}}\Delta tn$; where $n$ is the number of molecules per unit volume. Clearly, the total momentum transferred to the wall by these molecules in time $\Delta t$ is given by 

$Q=\left( 2m{{v}_{x}} \right)\left( \frac{1}{2}nA{{v}_{x}}\Delta t \right)$ 

The force on the wall refers to the rate of momentum transfer \[\frac{Q}{\Delta t}\] and pressure refers to the force per unit area: 

\[P=\frac{Q}{\left( A\Delta t \right)}=nmv_{x}^{2}\] 

In fact, all molecules in a gas do not have the same velocity; there is a distribution in velocities. The above equation therefore stands for pressure due to the group of molecules with speed ${{v}_{x}}$ in the $x-$direction and n stands for the number density of that group of molecules. The total pressure is obtained by summing over the contribution due to all groups: 

\[P=nm\bar{v}_{x}^{2}\] 

where \[\bar{v}_{x}^{2}\] is the average of \[v_{x}^{2}\]. 

Now the gas is isotropic, i.e., there is no preferred direction of velocity of the molecules in the vessel. Clearly, by symmetry, 

\[\bar{v}_{x}^{2}=\bar{v}_{y}^{2}=\bar{v}_{z}^{2}=\left( \frac{1}{3} \right)\left[ \bar{v}_{x}^{2}+\bar{v}_{y}^{2}+\bar{v}_{z}^{2} \right]=\frac{1}{3}{{\bar{v}}^{2}}\] 

Where, $v$ is the speed and \[{{\bar{v}}^{2}}\] denotes the mean of the squared speed. Thus, 

$P=\left( \frac{1}{3} \right)nm{{\bar{v}}^{2}}$ 

$\Rightarrow P=\frac{1}{3}mn{{\bar{v}}^{2}}=\frac{1}{3}\left( \frac{M}{V} \right){{\bar{v}}^{2}}=\frac{1}{3}\rho {{\bar{v}}^{2}}$ 

$M=\text{Total mass of gas molecules}$ 

$V=\text{Total volume of gas molecules}$

$\rho =$Total density of the gas molecules

2.4.1 Relation between Pressure and KE of Gas Molecules 

It is known that $P=\frac{1}{3}\left( \frac{M}{V} \right){{\bar{v}}^{2}}=\frac{1}{3}\rho {{\bar{v}}^{2}}$

Clearly, 

$P=\frac{2}{3}E$, where E is the mean kinetic energy of gas molecules

Thus, pressure exerted by an ideal gas is numerically equal to two thirds of mean kinetic energy of gas molecules.

2.4.2 Average KE per molecule of the Gas 

It is known that 

$P=\frac{1}{3}\left( \frac{M}{V} \right){{\bar{v}}^{2}}$

$\Rightarrow PV=\frac{1}{3}M{{\bar{v}}^{2}}$ 

Relating this with the Ideal gas equation; 

$nRT=\frac{1}{3}M{{\bar{v}}^{2}}$

$\Rightarrow nRT=\frac{1}{3}Nm{{\bar{v}}^{2}}$

$\Rightarrow \frac{3nRT}{2N}=\frac{1}{2}m{{\bar{v}}^{2}}$ 

Also, $N=n{{N}_{A}}$

$\Rightarrow \frac{3RT}{2{{N}_{A}}}=\frac{1}{2}m{{\bar{v}}^{2}}=\frac{3}{2}{{k}_{B}}T\left( \because R=N{{k}_{B}} \right)$ 

Clearly, the average kinetic energy of translation per molecule of the gas is$\frac{3}{2}{{k}_{B}}T$.

2.5 Kinetic Interpretation of Temperature 

From the above expressions, it can easily be seen that kinetic energy of one molecule is only dependent upon its temperature. Clearly, kinetic energy would cease when the temperature of the gas molecule becomes absolute zero.

Thus, absolute zero of a temperature is defined as the temperature at which the root mean square velocity of the gas molecule reduces to zero.

2.6 Derivation of Gas Laws from Kinetic Theory 

2.6.1 Boyle’s Law 

It is known that $PV=\frac{2}{3}N\bar{K}$

where $\bar{K}$ is the average kinetic energy of translation per gas molecule at constant temperature. 

$\bar{K}$ is constant for a provided mass of the gas. $N$ is also constant. Thus, $PV=$ constant for a provided mass of gas at constant temperature, which is known as the Boyle’s Law.

2.6.2 Charles’ Law 

It is known that \[PV=\frac{2}{3}N\bar{K}\] 

For a provided mass of gas, $N$ is constant.

As \[\bar{K}=\frac{3}{2}{{k}_{B}}T\Rightarrow \bar{K}\propto T\] and thus, $PV\propto T$, which is nothing but the Charles’ law.

2.6.3 Constant Volume Law

It is known that $PV=\frac{2}{3}N\bar{K}$

For a provided mass of gas, $N$ is constant. 

As \[\bar{K}=\frac{3}{2}{{k}_{B}}T\Rightarrow \bar{K}\propto T\]

Clearly, $PV\propto T$

Now, when $V$ is constant, $P\propto T$, which is nothing but the constant volume law.

2.6.4 Ideal Gas Equation 

Since $PV=\frac{2}{3}N\bar{K}$ and \[\bar{K}=\frac{3}{2}{{k}_{B}}T\]

\[\Rightarrow PV=\frac{2}{3}N\left( \frac{3}{2}{{k}_{B}}T \right)\] or \[PV=N{{k}_{B}}T\]

which is nothing but the ideal gas equation.

2.6.5 Avogadro’s Law

Consider two gases \[1\text{ and 2}\]. We may write: 

${{P}_{1}}{{V}_{1}}=\frac{2}{3}{{N}_{1}}{{\bar{K}}_{1}};{{P}_{2}}{{V}_{2}}=\frac{2}{3}{{N}_{2}}{{\bar{K}}_{2}}$ 

Suppose their pressures, volumes and temperatures are the same, then 

${{P}_{1}}={{P}_{2}};{{V}_{1}}={{V}_{2}};{{\bar{K}}_{1}}={{\bar{K}}_{2}}$ 

Clearly, ${{N}_{1}}={{N}_{2}}$ 

Thus, equal volumes of all ideal gases existing under the same conditions of temperature and pressure contain equal number of molecules, which is Avogadro’s Law or hypothesis. 

Alternatively, since \[PV=N{{k}_{B}}T\Rightarrow N=\frac{PV}{{{k}_{B}}T}\]

Now, when  \[P,V,\text{ and }T\] are constants, \[N\] also turns out to be constant.

2.6.6 Graham’s Law of Diffusion 

The rate \[(r)\] of diffusion of a gas through a porous pot or into another gas is evaluated by the rms speed of its molecules, i.e., 

$r\propto {{v}_{\text{rms}}}$ 

However, as ${{v}_{rms}}=\sqrt{\frac{3P}{\rho }}\Rightarrow r\propto \sqrt{\frac{3P}{\rho }}\Rightarrow r\propto \frac{1}{\sqrt{\rho }}$ 

Thus, if ${{r}_{1}}\text{ and }{{r}_{2}}$ are the rates of diffusion of two gases of densities ${{\rho }_{1}}\text{ and }{{\rho }_{2}}$ respectively, then,

$\frac{{{r}_{1}}}{{{r}_{2}}}=\frac{{{\rho }_{1}}}{{{\rho }_{2}}}$ 

Clearly, the rates of diffusion of two gases are inversely proportional to the square roots of their densities, which is nothing but Graham’s law of diffusion.

2.6.7 Dalton’s Law of Partial Pressures 

The kinetic theory of gases talks about the gas pressure as a cause of the bombardment of the walls of the containing vessel by molecules. In a mixture of ideal gases, we might therefore expect the total pressure $P$ to be the sum of the partial pressures $\left( {{P}_{1}},{{P}_{2}},.... \right)$ due to each gas, i.e., 

$P={{P}_{1}}+{{P}_{2}}+...=\frac{2}{3}\frac{{{N}_{1}}}{{{V}_{1}}}{{\bar{K}}_{1}}+\frac{2}{3}\frac{{{N}_{2}}}{{{V}_{2}}}{{\bar{K}}_{2}}+...$ 

\[\Rightarrow P=\frac{2}{3}\left( \frac{{{N}_{1}}}{{{V}_{1}}}{{{\bar{K}}}_{1}}+\frac{{{N}_{2}}}{{{V}_{2}}}{{{\bar{K}}}_{2}}+... \right)\]

In equilibrium, the average kinetic energy of the molecules of various gases will be equal, i.e., 

\[{{\bar{K}}_{1}}={{\bar{K}}_{2}}=\bar{K}=\frac{3}{2}{{k}_{B}}T\] 

Thus, 

\[\Rightarrow P=\frac{2}{3}\left( {{n}_{1}}+{{n}_{2}}+... \right)\left( \frac{3}{2}{{k}_{B}}T \right)=\left( {{n}_{1}}+{{n}_{2}}+... \right){{k}_{B}}T\]

Where, \[{{n}_{1}}=\frac{{{N}_{1}}}{{{V}_{1}}};{{n}_{2}}=\frac{{{N}_{2}}}{{{V}_{2}}},.....\] 

This represents Dalton's Law of partial pressures which suggests that the resultant pressure exerted by a mixture of gases or vapors which do not interact in any way is equal to the sum of their individual (i.e., partial) pressures. 

The following figure demonstrates a model explaining kinetic theory of gases. It is constructed in accordance with theory on one hand and real experimental observations on the other hand.

The above piece of information is tempting but false. Even though the equation in box IV is useful, it does not suggest anything new, since it results from combining equations in boxes II and III.

2.7 Internal Energy 

As already learnt in thermodynamics, internal Energy of any substance is the combination of potential energies and kinetic energies of all molecules inside a provided gas. 

• For real gases, 

\[\text{Internal energy}=\text{P}\text{.E of molecules}+\text{K}\text{.E of molecules}\] 

• For an ideal gas 

\[\text{Internal energy}=\text{K}\text{.E of molecules}\] 

Here, potential energy of molecules is zero as considered in kinetic theory postulates. There is no interaction between the molecules and thus, its interactional energy is zero.

2.8 Degree of Freedom 

The number of degrees of freedom of a dynamical system refers to the total number of co-ordinates or independent quantities required to describe completely the position and configuration of a system.

Examples: 

• A particle traveling in a straight line, say along the $X-$ axis needs only the $x$ coordinate to define itself. It has only one degree of freedom. 

• A particle in a plane needs $2$ coordinates, hence has $2$ degrees of freedom. 

Generally, when 

$A=$ number of particles in the system 

$R=$ number of independent relations among the particles 

$N=$ number of degrees of freedom of the system 

\[\Rightarrow N=3AR\]

2.8.1 Monoatomic Gases 

The molecules of a monatomic gas (like neon, argon, helium, etc.) consist only of one atom

\[A=1;R=0\Rightarrow N=3\] 

Here, for translational motion, there are 3 degrees of freedom.

2.8.2 Diatomic Gases

The molecules of a diatomic gas consist of two atoms.

$A=2$; 

If the distance between the two molecules is assumed fixed, then $R=1$.  

\[\Rightarrow N=5\] 

Here, there are $5$ degrees of freedom, which is a combination of $3$ translational energies and $2$ rotational energies.

When vibrational motion is also considered, then (only at very high temperatures);

$N=7$, in which $3$ accounts for translational, $2$ for rotational and $2$ for vibrational energy.

2.8.3 Triatomic Gas

The molecules of a triatomic gas consist of three atoms.

Case: Linear 

Here,

$A=3;R=2\Rightarrow \Rightarrow N=7$

Case: Non-Linear

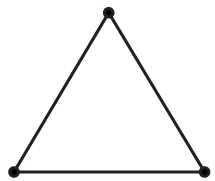
Here, 

$A=3;R=2\Rightarrow N=6$ 

Here again, vibrational energy is ignored.

2.8.4 Polyatomic Gas 

A polyatomic gas has \[3\] translational and \[3\] rotational degrees of freedom. Apart from them, when there are \[V\] vibrational modes, then there would be an additional \[2V\] vibrational degrees of freedom. Thus, total degrees of freedom is given by

\[N=3+3+2V=6+2V\]

2.9 Law of Equipartition of Energy 

Statement: For any dynamical system in thermal equilibrium, the total energy is distributed equally amongst all the degrees of freedom, and the energy associated with each molecule per degree of freedom is equal to \[\frac{1}{2}{{k}_{B}}T\], where \[{{k}_{B}}\] is Boltzmann constant and \[T\] is temperature of the system.

Application: $U=f\left( \frac{{{k}_{B}}T}{2} \right)$, where $f=$ total degrees of freedom. 

This law is very helpful in computing the total internal energy of any system, be it monoatomic, diatomic or any polyatomic. Once the internal energy is known, we can easily predict \[{{C}_{v}}\text{ and }{{C}_{P}}\] for such systems.

Remark: In case vibrational motion is also there in any system, say for a diatomic molecule, then there must be energy due to vibration as well, given by 

${{E}_{v}}=\frac{1}{2}m{{\left( \frac{dy}{dt} \right)}^{2}}+\frac{1}{2}k{{y}^{2}}$  

where, 

$\frac{dy}{dt}=$ Vibrational velocity 

$\frac{k{{y}^{2}}}{2}=$ Energy due to configuration 

Now, according to the law of equipartition, 

Energy per degree of freedom \[=\frac{1}{2}{{k}_{B}}T\].

$\Rightarrow TE=\frac{1}{2}{{k}_{B}}T+\frac{1}{2}{{k}_{B}}T={{k}_{B}}T$ is the total energy for one complete vibrational mode.

2.10 Specific Heat Capacity

With the information from the law of equipartition, we can predict the heat capacity of various gases.

2.10.1 Monoatomic Gas 

Here, degrees of freedom $=3$ 

Average energy of a molecule at temperature T is given by 

\[E=3\left( \frac{1}{2}{{k}_{B}}T \right)\] 

Energy for one mole $=E\times {{N}_{A}}$ 

$\Rightarrow U=\frac{3}{2}\left( {{k}_{B}}{{N}_{A}} \right)T$ 

$\Rightarrow U=\frac{3}{2}RT$

In thermodynamics, we have learnt that 

${{C}_{V}}={{\left. \frac{\Delta Q}{\Delta T} \right|}_{V}}=\frac{\Delta U}{\Delta T}$  [$\because W=0$ for constant $V$]

\[\Rightarrow {{C}_{V}}=\frac{3R}{2}\]

$\Rightarrow {{C}_{P}}=\frac{5R}{2}$ and $r=\frac{{{C}_{P}}}{{{C}_{V}}}=\frac{5}{3}$

2.10.2 Diatomic Gases 

When there is no vibration; 

Degrees of freedom $=5$  

Average energy for one mole $=\frac{5}{2}RT$

\[\Rightarrow {{C}_{V}}=\frac{\Delta U}{\Delta T}=\frac{5}{2}R\]

$\Rightarrow {{C}_{P}}=\frac{7R}{2}$

\[\Rightarrow r=\frac{{{C}_{P}}}{{{C}_{V}}}=\frac{7}{5}\]

On the other hand, when vibration is present; 

There is only one mode of vibration between $2$ molecules. 

Clearly, the degrees of freedom $=7$.

$\Rightarrow U=\frac{7}{2}RT$

$\Rightarrow {{C}_{V}}=\frac{7R}{2}$

$\Rightarrow {{C}_{P}}=\frac{9R}{2}$

$\Rightarrow r=\frac{9}{7}$

2.10.3 Polyatomic Gases 

Here, the degrees of freedom 

$=3$ for translational; 

$=3$ for rotational; 

$=2V$ for vibrational 

$\Rightarrow N=6+2V$ 

Where, $V=$ Number of vibrational modes 

$\Rightarrow U=(6+2V)K\frac{RT}{2}$ 

$\Rightarrow {{C}_{V}}=(3+V)R$ 

$\Rightarrow {{C}_{P}}=(4+V)R$ 

$\Rightarrow r=\frac{4+V}{3+V}$

2.10.4 Specific heat capacity of solids 

• In solids, there is very little difference between heat capacity at constant pressure or at constant volume. Thus, we do not differentiate between \[{{C}_{P}}\text{ and }{{C}_{V}}\] for solids. 

$\Rightarrow C=\frac{\Delta Q}{\Delta T}=\frac{\Delta U}{\Delta T}$ 

(As solids hardly expand)

Now, in solids, the atoms are arranged in array structures and they are not free to move independently like the atoms in gases. Clearly, the atoms in solids do not possess any translational or rotational degree of freedom.

However, the molecules do possess vibrational motion along the $3$ mutually perpendicular directions. 

Thus, for $1$ mole of a solid, there are ${{N}_{A}}$ number of atoms and the energy associated with every molecule $=3\left[ 2\times \frac{1}{2}{{k}_{B}}T \right]=3{{k}_{B}}T$. 

\[\Rightarrow U=3RT\] for one mole

$\Rightarrow C=\frac{\Delta Q}{\Delta T}=\frac{\Delta U}{\Delta T}=3R$ 

• The above equation is known as the law of Dulong and Petit.

• At low temperatures, the vibrational mode might not be that active and thus, heat capacity is low at low temperatures for solids.

2.10.5 Specific heat capacity of Water 

Consider water like a solid.

Water has three atoms, $2$ of hydrogen and one of oxygen.

The total degrees of freedom for every atom \[=3\times 2=6\]. 

Thus, the total degrees of freedom for every water molecule \[=3\times 2=18\].

$\Rightarrow C=\frac{\Delta Q}{\Delta T}=\frac{\Delta U}{\Delta T}=\frac{\left( 18\times \frac{1}{2}R\Delta T \right)}{\Delta T}$

$\Rightarrow C=9R$

2.11 Maxwell Law of Distribution of Molecules

Assumptions of Maxwell Distribution 

• Molecules of all velocities between $0\text{ to }\infty $ are present. 

• Velocity of one molecule continuously changes, though the fraction of molecules in one range of velocities is constant.

Result 

$N=4\pi N{{\left( \frac{M}{2\pi {{k}_{B}}T} \right)}^{\frac{3}{2}}}{{V}^{2}}{{e}^{-\frac{m{{V}^{2}}}{2{{k}_{B}}T}}}$ 

Where,

$N=\frac{dN}{dV}$ 

$dV=change\text{ }in\text{ }speed$ 

$dN=\text{Total number of molecules with speeds between V and V+dV}$ 

With respect to this, we define three types of speeds for molecules of gas. 

\[{{V}_{\text{rms}}}={{\left( {{{\bar{V}}}^{2}} \right)}^{\frac{1}{2}}}={{\left[ \frac{1}{N}\int{{{V}^{2}}dN(V)} \right]}^{\frac{1}{2}}}\] 

$\Rightarrow {{V}_{\text{rms}}}=\sqrt{\frac{3RT}{M}}$ 

Where, $M=\text{Molecular mass of gas}$ 

• Similarly,

\[{{V}_{\text{av}}}=\bar{V}=\frac{1}{N}\int{VdN}=\sqrt{\frac{8RT}{\pi M}}\]

• However, ${{V}_{MP}}$ is the velocity at which $\frac{dN}{dV}=0$. 

• Physically, ${{V}_{MP}}$ refers to the velocity possessed by the maximum number of molecules. 

Remarks: ${{V}_{\text{rms}}}>{{V}_{\text{av}}}>{{V}_{MP}}$

2.12 Mean Free Path 

The path traversed by a molecule between two successive collisions with another molecule is termed the free path. Mathematically, 

$\bar{l}=\frac{\text{Total distance travelled by a molecule }}{\text{Number of collisions it makes with other molecules}}$

Expression: 

Mean Free Path

Consider spherical molecules of a gas of diameter $d$. Concentrate on a single molecule with the average speed $<v>$. It would suffer collision with any molecule that comes within a distance $d$ between the centers. In a time period $\Delta t$, it sweeps a volume $\pi {{d}^{2}}<v>\Delta t$, wherein any other molecule would collide with it (as shown in figure). If n is the number of molecules per unit volume, the molecule suffers $n\pi {{d}^{2}}<v>\Delta t$ collisions in time $\Delta t$. Therefore, the rate of collisions is $n\pi {{d}^{2}}<v>$ or the time between two successive collisions is on the average.

$\Rightarrow \tau =\frac{1}{\left( n\pi <v>{{d}^{2}} \right)}$ 

The average distance between two successive collisions, termed the mean free path $\bar{1}$ is given by 

$\bar{1}=<v>\tau =\frac{1}{\left( n\pi {{d}^{2}} \right)}$

In this derivation, we considered the other molecules to be at rest. But in fact, all molecules are moving and the collision rate is computed by the average relative velocity of the molecules. Clearly, we need to replace $<v>$ by $<vr>$ in the above expression for a more exact treatment as follows: 

$\Rightarrow \bar{1}=\frac{1}{\left( \sqrt{2}n\pi {{d}^{2}} \right)}$

Result 

$\bar{1}=\frac{1}{\left( \sqrt{2}n\pi {{d}^{2}} \right)}$

Remark: Mean free path is dependent inversely on the number density and size of a molecule.

2.13 Brownian Motion 

The irregular movement of suspended particles like tiny dust particles or pollen grains in a liquid is termed Brownian motion.

Class 11 Physics Revision Notes for Chapter 11 - Thermodynamics

Students of class 11 can rely on Vedantu who are studying under the CBSE board for the preparation of questions and notes for their examination.

In Vedantu, CBSE Class 11 students are provided with an outstanding educational instrument in the form of NCERT solutions helping as the definitive guide for all the problems covered in the textbook.

Thermodynamics Class 11 Physics Notes

According to the CBSE syllabus, Class 11 Physics Revision Notes for the subject Thermodynamics is prepared. It consists of all the significant theories, along with their explanations. Thermodynamics is related to a very important chapter in physics.

(Image to be added soon)

As per the mass reviews, many students take this chapter as the most difficult to understand. We are here with the solution, and we are providing the CBSE Class 11 Physics Revision Notes for the chapter Thermodynamics. 

The preparation of this subject is taken care of by our experts. All the theories and questions are explained in detail for students’ easy understanding.

Class 11 Physics Chapter 11 Notes

Let’s discuss the Laws of Thermodynamics.

The laws of thermodynamics can be said as important physical quantities. They are just like energy, and temperature. Also, Entropy is the physical quantity that describes thermodynamic systems at thermal equilibrium.

There Are Four Laws of Thermodynamics, Such As:

Zeroth Law of Thermodynamics 

Zeroth law of thermodynamics explains the two systems that are in thermal equilibrium with the third system (the third system is not a part of the two systems) are in equilibrium with one another.

First Law of Thermodynamics

The first law of thermodynamics says that when we apply the law of conservation of energy to a system, then the energy transfer in that system occurs away or nearby the system with the help of heat and work.

From this law, we can manipulate the relationship between the change in the internal energy of the system, the work is done by the system, and heat supplied to the system.

Second Law of Thermodynamics

From the Second Law of thermodynamics, we obtain that it is impossible to find a system in which the absorption of heat from the reservoir is the total conversion of heat into work.

Third Law Of Thermodynamics 

According to the Third Law of thermodynamics, the system holds minimum energy at an absolute zero temperature.

Notes Of Chapter Thermodynamics Class 11 Physics

Sub-topics of Class 11 Physics Chapter 11 Thermodynamics

1. Introduction to thermodynamics

2. Thermal equilibrium

3. Heat, internal energy, and work

4. Zeroth law of Thermodynamics

5. Specific heat capacity

6. The first law of thermodynamics

7. The equation of state and Thermodynamic state variables 

8. Heat engines

9. Refrigerators and heat pumps

10. Thermodynamic processes

11. The second law of thermodynamics

12. Carnot Engine

13. Reversible and irreversible processes

CBSE Class 11 Physics Notes Chapter 11 Thermodynamics

What Do You Mean by Enthalpy?

According to thermodynamics, the measurement of energy is known as enthalpy. The total content of the heat of a system signifies the quantity of enthalpy. Enthalpy is the sum of the internal energy of the system and the product of volume and pressure.

Mathematically, H = E + PV

H = Enthalpy

E = Internal energy

P = Pressure of the system

V = Volume of the system

Download CBSE Class 11 Physics Notes Thermodynamics PDF

Interested students can download the physics notes of thermodynamics for Class 11 NCERT Notes PDF files from our website. The link is specified below.

Why Choose Vedantu for CBSE Class 11 Physics Notes?

Vedantu has provided some excellent features on the CBSE class 11 Physics delivered. The subsequent opinions can certainly give you a noble idea to pick the Vedantu as your study program partner.

1. Vedantu appoints many specialists who are best in a range of subjects. They do their hard work to prepare the CBSE class 11 Physics notes. This feature can also benefit the students very much.

2. The Vedantu has uploaded the pdf files on their website that comprise the CBSE class 11 Physics notes of the thermodynamics chapter. These notes are arranged in a systematic order and supportive of learning.

3. We are engaging the students to practice on the model papers of the CBSE class 11 Physics notes regularly. It can give them the ability to secure the best marks in their board exams.

4. In the Vedantu learning app, the CBSE class 11 Physics Pdf files contain many mathematical problems along with the proper concepts. All these questions are responded precisely by giving perfect clarification to each of them.