Physics Notes for Chapter 13 Oscillations Class 11 - FREE PDF Download
FAQs on Oscillations Class 11 Physics Chapter 13 CBSE Notes - 2025-26
1. What are the key concepts covered in Class 11 Physics Chapter 13 Oscillations Revision Notes?
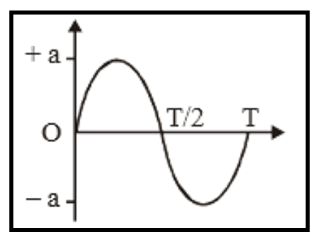
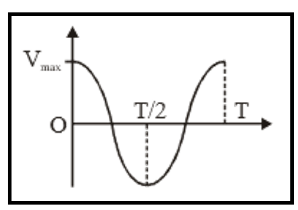
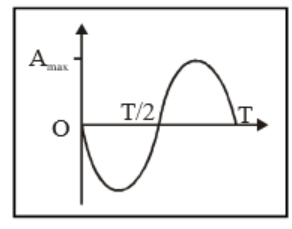
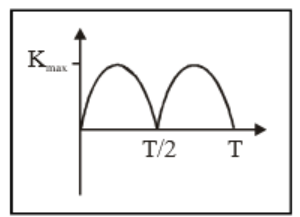
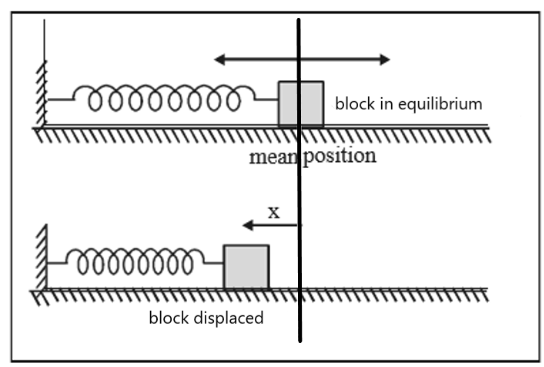
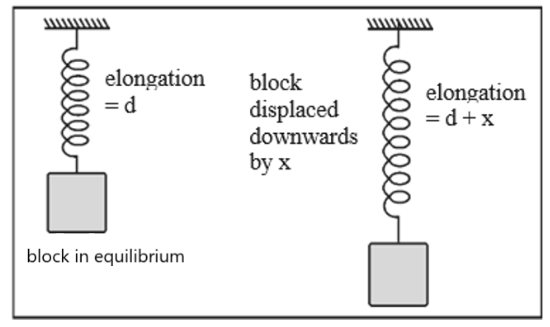
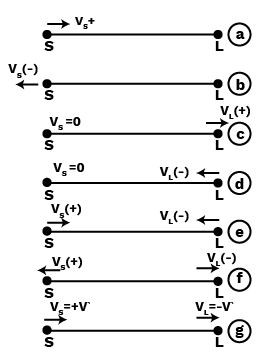
The Oscillations Class 11 Notes summarise core concepts such as periodic and oscillatory motion, simple harmonic motion (SHM), the mathematical equation of SHM, amplitude, frequency, time period, energy in SHM, and distinctions between damped and undamped oscillations. These notes also connect oscillatory motion to real-world systems like springs and pendulums and provide essential formulas for quick revision.
2. How can students use revision notes effectively for Physics Chapter 13 Oscillations?
To revise efficiently, students should:
- Begin by reviewing essential definitions and formulas highlighted in the notes.
- Use diagrams and concept maps to visualise relationships between amplitude, frequency, and phase.
- Solve illustrative examples and review solved problems to understand applications of formulas.
- Summarise main concepts after each section for last-minute recap.
- Regularly test themselves with concept checks or short questions to reinforce memory.
3. What is the revision order recommended for mastering the concepts in Oscillations?
The optimal order to revise Class 11 Physics Chapter 13 is:
- Start with periodic and oscillatory motions to build core understanding.
- Move to simple harmonic motion and its mathematical formulation.
- Study key terms: amplitude, time period, frequency, and phase.
- Review energy changes in SHM (kinetic & potential energy).
- Understand types of oscillations: damped vs. undamped, and practical examples like pendulums and springs.
- Lastly, connect oscillations to related advanced concepts (such as waves) for a holistic grasp.
4. How do revision notes help in connecting the topics within Chapter 13 and other chapters?
Revision notes for Oscillations highlight conceptual links between periodic motion, SHM, and subsequent topics like mechanical waves. By summarising relationships (such as between SHM and uniform circular motion), they help students see pattern recognition and formula similarities, making it easier to apply the knowledge to chapters like Waves and Sound.
5. What are the most important formulas and terms to include in a quick revision for Oscillations?
Essential revision items are:
- SHM Equation: x(t) = A cos(ωt + φ)
- Angular Frequency: ω = √(k/m)
- Time Period: T = 2π√(m/k)
- Frequency: f = 1/T
- Maximum Velocity: vmax = Aω
- Maximum Acceleration: amax = Aω2
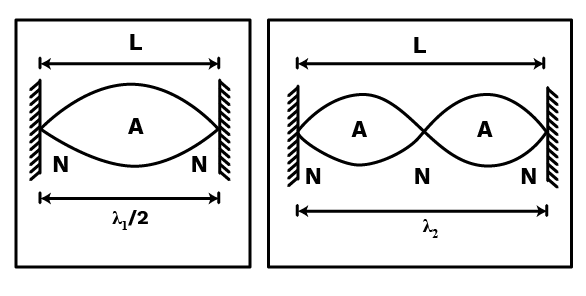
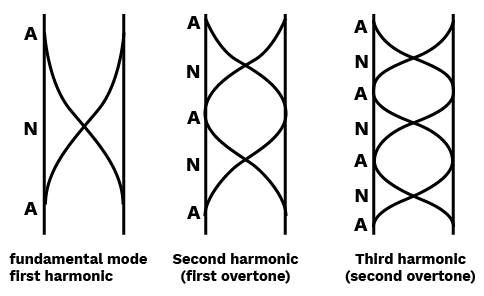
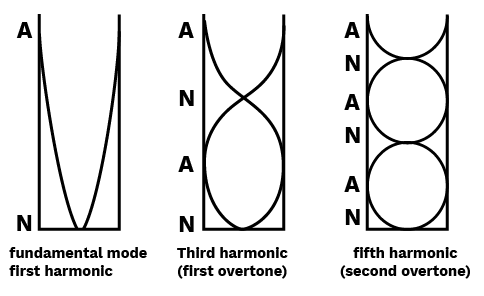
- Definitions: Amplitude, displacement, phase, restoring force, node, antinode.
6. What are common misconceptions students should avoid while revising Oscillations?
Students often confuse periodic motion with simple harmonic motion – not all periodic motions are SHM. Another misconception is assuming the time period depends on amplitude in SHM (it doesn't). Clarifying these in the notes prevents errors in understanding and problem-solving.
7. How does the concept map help in revising Oscillations?
A concept map visually organises definitions, formulas, relationships between motion types, and practical examples. Using it during quick revision ensures all major points are covered and shows how each idea connects, aiding long-term retention before exams.
8. Which revision strategies are most effective to prepare for conceptual questions on Oscillations?
Using short summaries for each concept, practicing with HOTS (Higher Order Thinking Skills) questions, comparing different oscillatory systems, and self-testing with derivations or graphs, all help in gaining conceptual mastery required for exams.
9. Why is it important to summarise solved examples in your revision notes for Physics Chapter 13?
Summarising key solved examples consolidates problem-solving patterns and clarifies how core formulas are applied to practical situations. This fast-tracks last-minute revision and enhances readiness for a wide range of exam questions.
10. What types of questions are best included in a rapid revision session for Oscillations?
Focus on:
- Definition and formula recall
- Short conceptual application questions
- Comparisons (such as damped vs. undamped oscillations)
- Quick numerical problems (e.g., finding time period, frequency, maximum speed or acceleration)
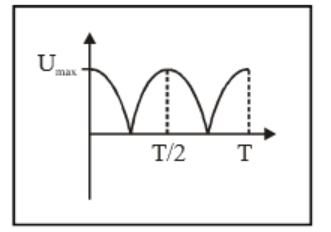
- Graph interpretation tasks