NCERT Exemplar for Class 11 Physics Chapter 12 - Thermodynamics (Book Solutions)

Exercise

MULTIPLE CHOICE QUESTIONS-I

1. An ideal gas undergoes four different processes from the same initial state (Figure 12.1). Four processes are adiabatic, isothermal, isobaric and isochoric. Out of 1, 2, 3 and 4, which one is adiabatic?

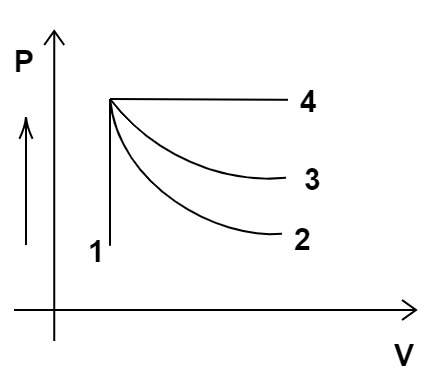
(a) 4

(b) 3

(c) 2

(d) 1

Ans: Option (c)

Graph represents that volume remains constant in process 1 and pressure remains constant in process 4. So, process 4 is isobaric and process 1 is isochoric. Now, out of processes 2 and 3, process 2 has more slope. Adiabatic process has more slope than the isothermal process. Hence, process 2 is an adiabatic process. 

2. If an average person jogs, he produces $14.5 \times {10^3}\dfrac{{cal}}{{\min }}$. This is removed by the evaporation of sweat. The amount of sweat evaporated per minute (assuming $1kg$ requires $580 \times {10^3}cal$ for evaporation).

(a) $0.025kg$

(b) $2.25kg$

(c) $0.05kg$

(d) $0.20kg$

Ans: Option (a) 

We are given that $1kg$ of sweat requires $580 \times {10^3}cal$ for evaporation. So, we will follow a unitary method to find the amount of sweat evaporated per minute from the body.

So, $1cal$ will produce sweat $ = \dfrac{1}{{580 \times {{10}^3}}}kg$

Now, $14.5 \times {10^3}cal$ will produce sweat $ = \dfrac{{14.5 \times {{10}^3}}}{{580 \times {{10}^3}}}kg$

$ = \dfrac{1}{{40}}kg = 0.025kg$

So, the amount of sweat evaporated per minute is $0.025kg$.

3. Consider the P-V diagram for an ideal gas shown in Figure 12.2.

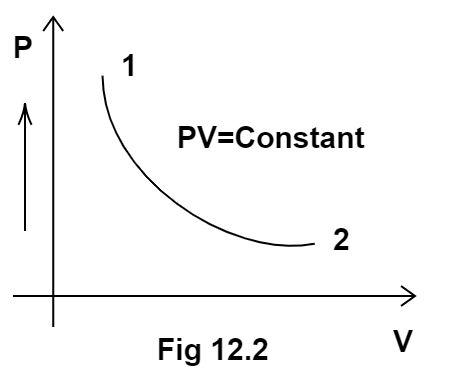
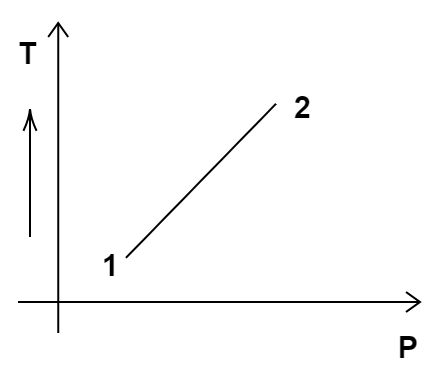
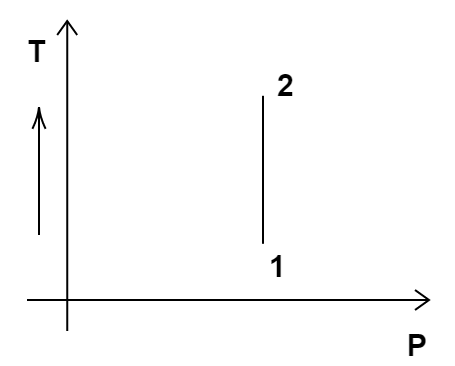
Out of the following diagrams (Figure), which represents the T-P diagram?

(i)

(ii)

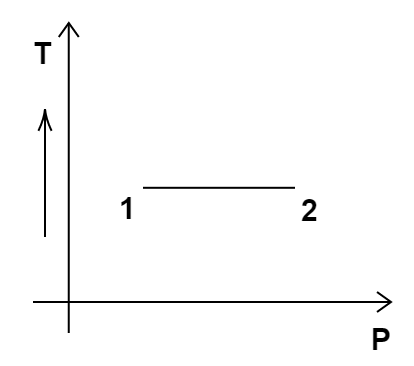
(iii)

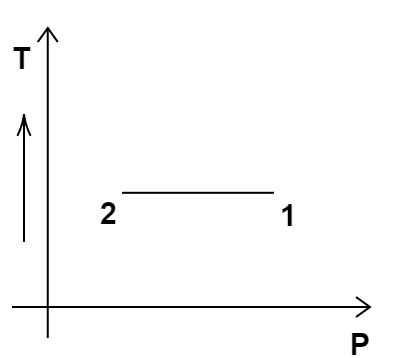
(iv)

(a) (i)

(b) (ii)

(c) (iii)

(d) (iv)

Ans: option (c) 

According to the P-V diagram provided in the question, P increases as V decreases at constant temperature. So, it is Boyle's law. So, temperature will remain constant in the TP graph and pressure will be higher at stage 1 than at stage 2. So, we get the option (c) as the correct answer. 

4. An ideal gas undergoes a cyclic process ABCDA as shown in the given PV diagram. The amount of work done by the gas is:

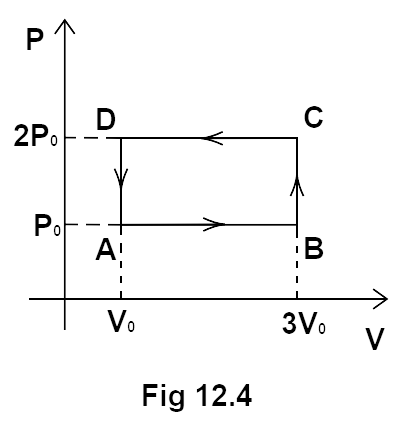
(a) $6{P_0}{V_0}$

(b) $ - 2{P_0}{V_0}$

(c) $2{P_0}{V_0}$

(d) $4{P_0}{V_0}$

Ans: option (b) 

We can calculate the magnitude of the work done by calculating the area of the rectangle formed in the graph. 

So, we get,

Area of loop $ = \left( {2{P_0} - {P_0}} \right)\left( {3{V_0} - {V_0}} \right)$

\[ =  - 2{P_0}{V_0}\]

Since, the direction of arrows is anticlockwise. This means that the work done is negative. 

Hence, option (b) is the correct answer. 

5. Consider two containers A and B containing identical gases at the same pressure, volume and temperature. The gas in container A is compressed to half of its original volume isothermally while the gas in container B is compressed to half of its original value adiabatically. The ratio of final pressure of gas in B to that of gas in A is:

(a) ${2^{\gamma  - 1}}$

(b) ${\left( {\dfrac{1}{2}} \right)^{\gamma  - 1}}$

(c) ${\left( {\dfrac{1}{{1 - \gamma }}} \right)^2}$

(d) $ - {\left( {\dfrac{1}{{\gamma  - 1}}} \right)^2}$

Ans: option (a) 

In the processes taking place in containers A and B, gas is being compressed from the same initial stage through two different paths. 

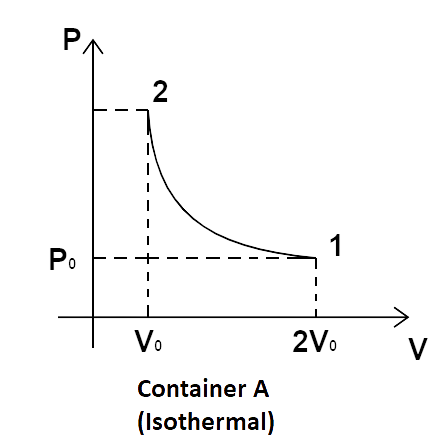
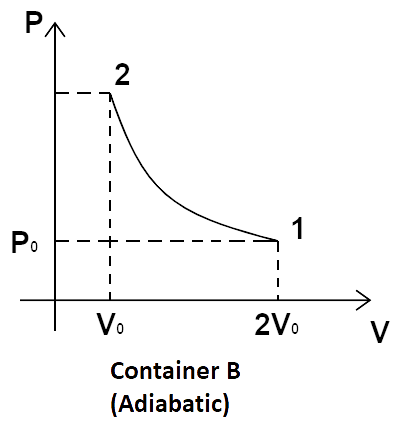
Now, for the isothermal process in container A, we have, ${P_1}{V_1} = {P_2}{V_2}$.

So, we get, \[{P_0}\left( {2{V_0}} \right) = {P_2}{V_0}\]

\[ \Rightarrow {P_2} = 2{P_0}\]

Now, for adiabatic processes, \[{P_1}{V_1}^\gamma  = {P_2}{V_2}^\gamma \].

Now, substituting the known values, we get,

\[{P_0}{\left( {2{V_0}} \right)^\gamma } = {P_2}{\left( {{V_0}} \right)^\gamma }\]

\[ \Rightarrow {P_2} = {\left( {\dfrac{{2{V_0}}}{{{V_0}}}} \right)^\gamma }{P_0} = {2^\gamma }{P_0}\]

So, \[\dfrac{{{{\left( {{P_2}} \right)}_B}}}{{{{\left( {{P_2}} \right)}_A}}} = \dfrac{{{2^\gamma }{P_0}}}{{2{P_0}}} = {2^{\gamma  - 1}}{P_0}\]

Hence, option a is the correct answer. 

6. Three copper blocks of masses \[{M_1}\], \[{M_2}\] and \[{M_3}\] kg respectively are brought into thermal contact till they reach equilibrium. Before contact, they were at ${T_1}$, \[{T_2}\], and \[{T_3}\]\[\left( {{T_1} > {T_2} > {T_3}} \right)\].Assuming there is no heat loss to the surroundings, the equilibrium temperature T is (s is specific heat of copper)

(a) $T = \dfrac{{{T_1} + {T_2} + {T_3}}}{3}$

(b) $T = \dfrac{{{M_1}{T_1} + {M_2}{T_2} + {M_3}{T_3}}}{{{M_1} + {M_2} + {M_3}}}$

(c) $T = \dfrac{{{M_1}{T_1} + {M_2}{T_2} + {M_3}{T_3}}}{{3\left( {{M_1} + {M_2} + {M_3}} \right)}}$

(d) $T = \dfrac{{{M_1}T{s_1} + {M_2}{T_2}s + {M_3}{T_3}s}}{{{M_1} + {M_2} + {M_3}}}$

Ans: Option (b) 

Let the equilibrium temperature to be found be T.Now, we considerT to be greater than${T_1}$ and \[{T_2}\] but smaller than \[{T_3}\].

Since there is no loss of heat energy. Hence, we get,

Heat lost by \[{M_3}\]$ = $ Heat regained by \[{M_1}\]$ + $ Heat regained by \[{M_2}\]

So, we get, 

\[ \Rightarrow {M_3}s\left( {{T_3} - T} \right) = {M_1}s\left( {T - {T_1}} \right) + {M_2}s\left( {T - {T_2}} \right)\]

Dividing both sides by s, we get,

\[ \Rightarrow {M_3}\left( {{T_3} - T} \right) = {M_1}\left( {T - {T_1}} \right) + {M_2}\left( {T - {T_2}} \right)\]

Opening the brackets and solving for T, we get,

\[ \Rightarrow {M_3}{T_3} - {M_3}T = {M_1}T - {M_1}{T_1} + {M_2}T - {M_2}{T_2}\]

\[ \Rightarrow {M_3}{T_3} + {M_1}{T_1} + {M_2}{T_2} = {M_1}T + {M_2}T + {M_3}T\]

\[ \Rightarrow T = \dfrac{{{M_1}{T_1} + {M_2}{T_2} + {M_3}{T_3}}}{{{M_1} + {M_2} + {M_3}}}\]

Hence, b is the correct option. 

MULTIPLE CHOICE QUESTIONS-II

7. Which of the processes described below are irreversible? 

(a) The increase in temperature of an iron rod by hammering it. 

(b) A gas in a small container at a temperature T1 is brought in contact with a big reservoir at a higher temperature T2 which increases the temperature of the gas. 

(c) A quasi-static isothermal expansion of an ideal gas in a cylinder fitted with a frictionless piston. 

(d) An ideal gas is enclosed in a piston cylinder arrangement with adiabatic walls. A weight W is added to the piston, resulting in compression of gas.

Ans: options (a), (b) and (d) 

(a) When we hammer an iron rod, the work done on the rod is converted into heat energy. We cannot convert this heat energy back into work. Hence, the process is irreversible. 

(b) The heat flows from the bigger container to the smaller container till the system reaches an equilibrium and the temperature of both become equal. But we cannot transfer the heat energy from the smaller container to the bigger container as heat flows from higher temperature to lower temperature. Hence, the process is irreversible. 

(c) The expansion of an ideal gas in quasi-static isothermal conditions can be reversed. Hence, it is not an irreversible process.

(d) The volume of the gas is decreased and the pressure is increased as we add weight to the piston. So, it can be reversed on its own. Hence, it is an irreversible process. 

Therefore, options a, b and d are irreversible processes. 

8. An ideal gas undergoes isothermal process from some initial state i to final state f. Choose the correct alternatives.

(a) $dU = 0$

(b) $dQ = 0$

(c) $dU = dQ$

(d) $dW = dQ$

Ans: options (a) and (d) 

Since the gas under consideration is ideal in nature and the process followed is isothermal. So, we have, $\Delta T = 0$.

So, T remains constant for the process. 

Now, $dU = n{C_v}dT = 0$

Also, $dQ = dU + dW$

$ \Rightarrow dQ = dW$

Hence, options (a) and (d) are correct choices. 

9. 

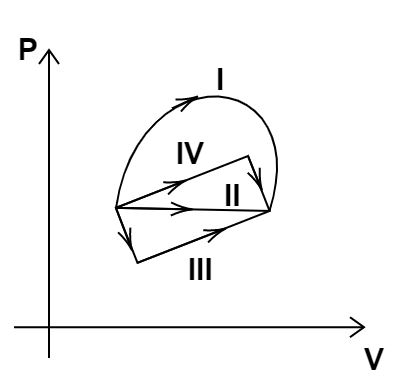
(a) Change in internal energy is same in IV and III cases, but not in I and II. 

(b) Change in internal energy is the same in all the four cases. 

(c) Work done is maximum in case I 

(d) Work done is minimum in case II

Ans: options (b) and (c) 

Change in internal energy depends only upon the initial and final positions and not on the path followed. Hence, change in internal energy is the same for all the cases. The work done is dependent upon the path followed. Work done is the area enclosed by the path with the x axis. Since path I encloses the maximum area with x axis, the work done is maximum in case I. 

Hence, options (b) and (c) are the correct answers. 

10. Consider a cycle followed by an engine see (Figure). 

1 to 2 is isothermal 

2 to 3 is adiabatic 

3 to 1 is adiabatic

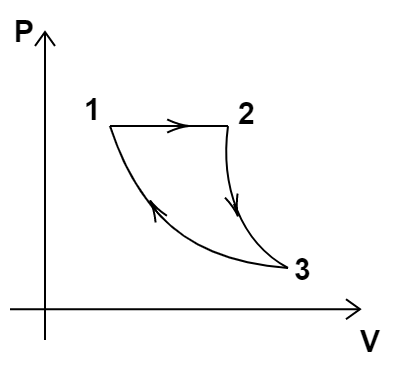
Such a process does not exist because 

(a) Heat is completely converted to mechanical energy in such a process, which is not possible. 

(b) Mechanical energy is completely converted to heat in this process, which is not possible. 

(c) Curves representing two adiabatic processes don’t intersect. 

(d) Curves representing an adiabatic process and an isothermal process don’t intersect.

Ans: option (a) 

The entire cyclic process starts with an initial position as 1 and ends up at the same position. This means that there is no change in the internal energy as it depends only upon the initial and final positions. 

Now, $dU = 0$

So, $dQ = dU + dW$

$ \Rightarrow dQ = dW$

This shows that all the heat energy gets converted into mechanical energy which is not in accordance with the second law of thermodynamics. 

Hence, option (a) is the correct answer. 

11. Consider a heat engine as shown in Figure, \[{Q_1}\] and \[{Q_2}\] are heat added to heat bath \[{T_1}\] and heat taken from \[{T_2}\] in one cycle of engine. W is the mechanical work done on the engine.

If $W > 0$, then the possibilities are: 

(a) ${Q_1} > {Q_2} > 0$

(b) ${Q_2} > {Q_1} > 0$

(c) \[{Q_2} < {Q_1} < 0\]

(d) ${Q_1} < 0$ and \[{Q_2} > 0\]

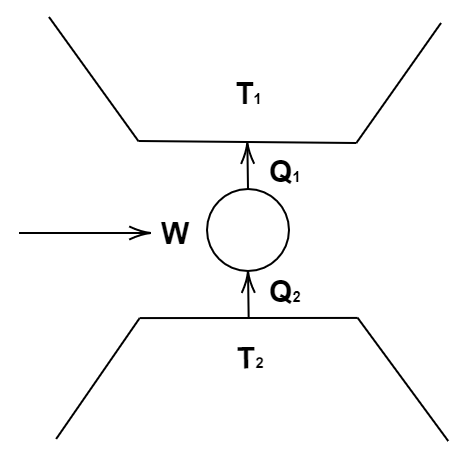
Ans: options (a) and (c) 

Now, according to the conservation of heat energy, we have, ${Q_1} = W + {Q_2}$. 

Now, $W > 0$. So, we have, ${Q_1} - {Q_2}$ as positive. 

This can be possible when \[{Q_1} > {Q_2}\] if both of them are positive. So, we have, ${Q_1} > {Q_2} > 0$. 

Also, this can be possible if both of them are negative as \[{Q_2} < {Q_1} < 0\].

Hence, options (a) and (c) are the correct answers. 

12. Can a system be heated and its temperature remains constant?

Ans: If the system utilises the entire heat energy supplied in doing the work against the surroundings, then there will be no change in the internal energy of the system and the temperature will remain constant. 

13. A system goes from P to Q by two different paths in the P-V diagram as shown in Figure. Heat given to the system in path 1 is\[1000J\]. The work done by the system along path 1 is more than path 2 by \[100J\]. What is the heat exchanged by the system in path 2?

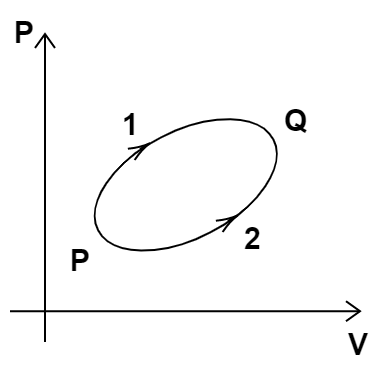
Ans: Since the initial and final positions of both the paths are the same. Hence, the change in internal energy for both the processes will be the same.

Now, we are given that \[{Q_1} = 1000J\] and \[{W_1} - {W_2} = 100J\].

$\Delta U$ will be the same for both paths. 

We calculate the internal energy change in path 1.

So, \[{Q_1} = \Delta {U_1} + {W_1}\]

Substituting the known values, we get,

\[ \Rightarrow 1000J = \Delta {U_1} + {W_1}\]

Now, we calculate the heat energy exchanged in path 2. So, we get, 

\[{Q_2} = \Delta {U_2} + {W_2}\]

Now, using $\Delta {U_1} = \Delta {U_2}$ and \[{W_1} - 100{J_2} = {W_2}\], we get,

\[ \Rightarrow {Q_2} = \Delta {U_2} + {W_1} - 100J\]

\[ \Rightarrow {Q_2} = 1000J - 100J = 900J\]

14. If a refrigerator’s door is kept open, will the room become cool or hot? Explain.

Ans: The temperature of the room will increase and the room will become hot if a refrigerator’s door is left open. This is because the refrigerator, being a heat engine, extracts the heat from lower temperature and transfers to higher temperature. If a refrigerator’s door is kept open, the refrigerator will transfer more heat inside the room than earlier. 

15. Is it possible to increase the temperature of a gas without adding heat to it? Explain.

Ans: In the process of compressing the gas adiabatically there is a rise in temperature while no heat is transferred to the system. This is because the negative work done is balanced by the change in internal energy which makes the temperature of the gas rise. 

16. Air pressure in a car tyre increases during driving. Explain.

Ans: During driving, the temperature of the gas inside the tyres increases due to the application of the reaction force on the tyres. But the volume of gas inside the tyre is constant. So, according to the Charles law$P \propto T$, the air pressure of car tyres increases.

SHORT ANSWER TYPE QUESTIONS

17. Consider a Carnot’s cycle operating between \[{T_1} = 500K\] and \[{T_2} = 300K\] producing \[1\,kJ\] of mechanical work per cycle. Find the heat transferred to the engine by the reservoirs.

Ans: efficiency of a Carnot engine is calculated as \[\mu  = \left( {1 - \dfrac{{{T_2}}}{{{T_1}}}} \right)\].

Substituting the known values into the formula, we get,

\[ \Rightarrow \mu  = \left( {1 - \dfrac{{300}}{{500}}} \right)\]

\[ \Rightarrow \mu  = \left( {1 - \dfrac{3}{5}} \right) = \dfrac{2}{5}\]

Now, we know that efficiency of the engine $ = \left( {\dfrac{{{\text{Output work}}}}{{{\text{Input work}}}}} \right)$.

Also, we are given output work as \[1\,kJ = 1000J\].

So, we get, 

$\dfrac{2}{5} = \left( {\dfrac{{{\text{1000J}}}}{{{\text{Input work}}}}} \right)$

So, ${\text{Input work}} = {\text{2500J}}$

Hence, heat transferred to the engine by the reservoir is ${\text{2500J}}$.

18. A person of mass \[60\] kg wants to lose $5$kg by going up and down a \[10m\] high stairs. Assume he burns twice as much fat while going up than coming down. If $1$ kg of fat is burnt on expending $7000Kcal$, how many times must he go up and down to reduce his weight by $5$ kg?

Ans) Potential energy gained in going up 10m high stairs $ = mgh = 60 \times 10 \times 10J = 6000J$

So, energy consumed to go up one time $ = 6000J$

Energy consumed to go down one time $ = \dfrac{{6000}}{2}J = 3000J$

Hence, energy consumed in going up and down the stairs once $ = 9000J$

Now, we convert the energy from joules to calories. Hence, we get,

Energy consumed in going up and down the stairs once in calories $ = \dfrac{{9000}}{{4.2}}cal$

Energy to be consumed or burning $1$ kg fat is $7000Kcal$.

So, energy to be consumed for burning $5$kg fat $ = 5 \times 7000Kcal = 35000Kcal$

Now, let the number of times the person has to go up and down the stairs to burn $5$kg fat be x. Then, we get,

$ \Rightarrow \left( x \right) \times \dfrac{{9000}}{{4.2}}cal = 35000 \times {10^3}cal$

$ \Rightarrow x = 35000 \times \dfrac{{4.2}}{9}$

$ \Rightarrow x = 16333.33$

Rounding off to the next integer, the person will have to go up and win the stairs $16334$ times.

19. Consider a cycle tyre being filled with air by a pump. Let V be the volume of the tyre (fixed) and at each stroke of the pump $\Delta V$ of air is transferred to the tube adiabatically. What is the work done when the pressure in the tube is increased from ${P_1}$ to ${P_2}$?

Ans: Since the process is adiabatic. So, we have, ${P_1}{V_1}^\gamma  = {P_2}{V_2}^\gamma $.

Now, let volume of the tyre after pumping one stroke is $V + dV$ and pressure is increased by $dP$. So, we get,

$P{\left( {V + dV} \right)^\gamma } = \left( {P + dP} \right){V^\gamma }$

$ \Rightarrow P{V^\gamma }{\left( {1 + \dfrac{{dV}}{V}} \right)^\gamma } = \left( {P + dP} \right){V^\gamma }$

$ \Rightarrow P{\left( {1 + \dfrac{{dV}}{V}} \right)^\gamma } = \left( {P + dP} \right)$

Neglecting the higher power terms as $dV <  < V$. Hence, we get,

$ \Rightarrow P\left( {1 + \gamma \dfrac{{dV}}{V}} \right) = P\left( {1 + \dfrac{{dP}}{P}} \right)$

$ \Rightarrow \left( {1 + \gamma \dfrac{{dV}}{V}} \right) = \left( {1 + \dfrac{{dP}}{P}} \right)$

$ \Rightarrow dV = \dfrac{{VdP}}{{\gamma P}}$

We know that work done is $\int {PdV} $. So, we get,

$ \Rightarrow \int {dW}  = \int {\dfrac{{VdP}}{\gamma }} $

Since the volume of the tire is constant. So, we get,

$ \Rightarrow W = \dfrac{V}{\gamma }\left( {{P_2} - {P_1}} \right)$

20. In a refrigerator one removes heat from a lower temperature and deposits to the surroundings at a higher temperature. In this process, mechanical work has to be done, which is provided by an electric motor. If the motor is of \[1kW\] power, and heat is transferred \[ - {3^ \circ }C\] to \[{27^ \circ }C\], find the heat taken out of the refrigerator per second assuming its efficiency is $50\% $ of a perfect engine.

Ans: So, Temperature of the source $ = {T_1} =  - {3^ \circ }C = \left( {273 - 3} \right)K = 270K$

Temperature of surroundings $ = {T_2} = {27^ \circ }C = \left( {273 + 27} \right)K = 300K$

We first find the efficiency of a perfect Carnot engine functioning at the temperatures given in the question. So, we have, 

Efficiency $ = \mu  = 1 - \dfrac{{{T_2}}}{{{T_1}}} = 1 - \dfrac{{270}}{{300}} = \dfrac{{30}}{{300}} = \dfrac{1}{{10}}$

Now, we are given that the refrigerator works at $50\% $efficiency of a perfect engine. So, we get the efficiency of the refrigerator as $50\% $of$\dfrac{1}{{10}}$$ = \eta  = \dfrac{{50}}{{100}} \times \dfrac{1}{{10}} = \dfrac{1}{{20}} = 0.05$.

Now, we calculate the coefficient of performance to find the work converted into heat taken out of the refrigerator per second. 

Hence, we have, $\beta  = \dfrac{{1 - \eta }}{\eta } = \dfrac{{1 - 0.05}}{{0.05}} = 19$

This means that $19$ percent of the work done by motor is converted to energy.

Hence, heat taken out of the refrigerator per second$ = 19 \times 1kW = 19\dfrac{{kJ}}{s}$.

21. If the coefficient of performance of a refrigerator is 5 and operates at the room temperature \[{27^ \circ }C\], find the temperature inside the refrigerator.

Ans: So, temperature of surroundings \[ = {T_1} = \left( {27 + 273} \right)K = 300K\]

We have the formula for the coefficient of performance as \[\beta  = \dfrac{{{T_2}}}{{{T_1} - {T_2}}}\].

So, substituting the known values, we get,

\[ \Rightarrow 5 = \dfrac{{{T_2}}}{{300K - {T_2}}}\]

\[ \Rightarrow 1500K = 6{T_2}\]

\[ \Rightarrow {T_2} = 250K\]

Hence, temperature inside the refrigerator \[ = {T_2} = 250K = {\left( {250 - 273} \right)^ \circ }C =  - {23^ \circ }C\]

22. The initial state of a certain gas is$\left( {{P_i},{V_i},{T_i}} \right)$ It undergoes expansion till its volume becomes ${V_f}$. Consider the following two cases:

(a) The expansion takes place at constant temperature. 

Ans: The temperature remains constant in case (a) as the gas expands from volume ${V_i}$ to volume ${V_f}$. Hence, we have, ${P_i}{V_i} = {P_f}{V_f}$ using the ideal gas equation $PV = nRT$. 

(b) The expansion takes place at constant pressure. Plot the P-V diagram for each case. In which of the two cases, is the work done by the gas more?

Ans: The expansion takes place at constant pressure. So, the process is isobaric and the PV graph will be parallel to the volume axis till the volume becomes ${V_f}$. The PV diagram for both the cases are as follows:

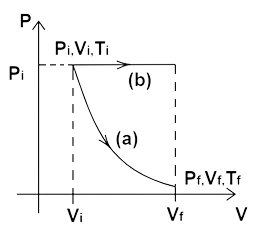
Also, the area under the PV diagram of case (b) is more. Hence, more work is done in process (b) than in process (a). 

LONG ANSWER TYPE QUESTIONS

23. Consider a P-V diagram in which the path followed by one mole of perfect gas in a cylindrical container is shown in Figure.

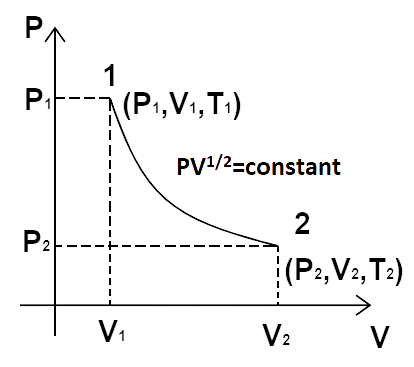
(a) Find the work done when the gas is taken from state $1$ to state $2$. 

Ans: We have, $P{V^{\dfrac{1}{2}}}$ = constant = $K$ or ${P_1}V_1^{\dfrac{1}{2}} = {P_2}V_2^{\dfrac{1}{2}} = K$ and $P = \dfrac{K}{{{V^{\dfrac{1}{2}}}}}$ 

Work done for process from $1$ to $2$ 

$ \Rightarrow WD = \int\limits_{{V_1}}^{{V_2}} {P.dV} $ 

$ \Rightarrow WD = \int\limits_{{V_1}}^{{V_2}} {\dfrac{K}{{{V^{\dfrac{1}{2}}}}}.dV} $

$ \Rightarrow WD = K\int\limits_{{V_1}}^{{V_2}} {{V^{ - \dfrac{1}{2}}}.dV} $

$ \Rightarrow WD = K\left[ {\dfrac{{\dfrac{{{V^{\dfrac{1}{2}}}}}{1}}}{2}} \right]_{{V_1}}^{{V_2}}$

$ \Rightarrow WD = 2K\left[ {\sqrt {{V_2}}  - \sqrt {{V_1}} } \right]$

Work done from ${V_1}$ to ${V_2}$, i.e., $dW = 2{P_1}V_1^{\dfrac{1}{2}}\left[ {\sqrt {{V_2}}  - \sqrt {{V_1}} } \right]$ 

$ = 2{P_2}V_2^{\dfrac{1}{2}}\left[ {\sqrt {{V_2}}  - \sqrt {{V_1}} } \right]$

(b) What is the ratio of temperature $\dfrac{{{T_1}}}{{{T_2}}}$ if ${V_2} = 2{V_1}$? 

Ans: From gas equation of ideal gas, we have $PV = nRT$ 

$ \Rightarrow T = \dfrac{{PV}}{{nR}}$ 

$ \Rightarrow T = \dfrac{{P\sqrt V \sqrt V }}{{nR}}$

$ \Rightarrow T = \dfrac{{K\sqrt V }}{{nR}}$

$ \Rightarrow {T_1} = \dfrac{{K\sqrt {{V_1}} }}{{nR}}$ and ${T_2} = \dfrac{{K\sqrt {{V_2}} }}{{nR}}$

$ \Rightarrow \dfrac{{{T_1}}}{{{T_2}}} = \dfrac{{\dfrac{{K\sqrt {{V_1}} }}{{nR}}}}{{\dfrac{{K\sqrt {{V_2}} }}{{nR}}}}$

$ \Rightarrow \dfrac{{{T_1}}}{{{T_2}}} = \dfrac{{\sqrt {{V_1}} }}{{\sqrt {{V_2}} }}$

Given that, ${V_2} = 2{V_1}$. Therefore, we get

$ \Rightarrow \dfrac{{{T_1}}}{{{T_2}}} = \dfrac{{\sqrt {{V_1}} }}{{\sqrt {2{V_1}} }}$

$ \Rightarrow \dfrac{{{T_1}}}{{{T_2}}} = \dfrac{1}{{\sqrt 2 }}.....\left( {ii} \right)$

Thus, the required ratio is $1:\sqrt 2 $ 

(c) Given the internal energy for one mole of gas at temperature T is$\dfrac{3}{2}RT$, find the heat supplied to the gas when it is taken from state (1) to (2) with ${V_2} = 2{V_1}$.

Ans: Given that, internal energy $U$ of gas is $U = \dfrac{3}{2}RT$ 

$ \Rightarrow \Delta U = \dfrac{3}{2}RdT$

$ \Rightarrow \Delta U = \dfrac{3}{2}R\left( {{T_2} - {T_1}} \right)$

From part (b), we have ${T_2} = \sqrt 2 {T_1}$.

$ \Rightarrow \Delta U = \dfrac{3}{2}R\left( {\sqrt 2 {T_1} - {T_1}} \right)$

$ \Rightarrow \Delta U = \dfrac{3}{2}R{T_1}\left( {\sqrt 2  - 1} \right)$

From part (a), we have $dW = 2{P_1}V_1^{\dfrac{1}{2}}\left[ {\sqrt {{V_2}}  - \sqrt {{V_1}} } \right]$

Given that, ${V_2} = 2{V_1}$. Therefore, we get

$ \Rightarrow \sqrt {{V_2}}  = \sqrt 2 \sqrt {{V_1}} $

$ \Rightarrow dW = 2{P_1}V_1^{\dfrac{1}{2}}\left[ {\sqrt 2 \sqrt {{V_1}}  - \sqrt {{V_1}} } \right]$

$ \Rightarrow dW = 2{P_1}V_1^{\dfrac{1}{2}}\sqrt {{V_1}} \left[ {\sqrt 2  - 1} \right]$

$ \Rightarrow dW = 2{P_1}{V_1}\left[ {\sqrt 2  - 1} \right]$

We know that ${P_1}{V_1} = nR{T_1}$. Therefore, we get

$ \Rightarrow dW = 2nR{T_1}\left[ {\sqrt 2  - 1} \right]$

Given that, $n = 1$. Therefore, we get

$ \Rightarrow dW = 2R{T_1}\left( {\sqrt 2  - 1} \right)$

$\therefore dQ = dW + dU$ 

$ \Rightarrow dQ = 2R{T_1}\left( {\sqrt 2  - 1} \right) + \dfrac{3}{2}R{T_1}\left( {\sqrt 2  - 1} \right)$

$ \Rightarrow dQ = R{T_1}\left( {\sqrt 2  - 1} \right)\left( {2 + \dfrac{3}{2}} \right)$

$ \Rightarrow dQ = R{T_1}\left( {\sqrt 2  - 1} \right)\left( {\dfrac{{4 + 3}}{2}} \right)$

$ \Rightarrow dQ = \dfrac{7}{2}R{T_1}\left( {\sqrt 2  - 1} \right)$

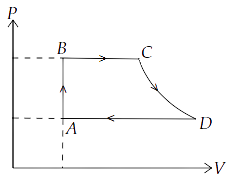
24. A cycle followed by an engine (made of one mole of perfect gas in a cylinder with a piston) is shown in Figure.

A to B: volume constant

B to C: adiabatic

C to D: volume constant

D to A: adiabatic

${V_C} = {V_D} = 2{V_A} = 2{V_B}$ 

(a) In which part of the cycle heat is supplied to the engine from outside?

Ans: Heat is supplied to the engine in part AB, in which $dV = 0$.

We know that $dW = P.dV$. Therefore, we get

$ \Rightarrow dW = P.0$

$ \Rightarrow dW = 0$

By first law of thermodynamics, $dQ = dU + dW$ 

$ \Rightarrow dQ = dU + 0$ or $dQ = dU$

The internal energy, $dU$ of the gas or system is increased as heat energy supplied to the system doesn’t work.

$\therefore P = \dfrac{{nRT}}{V}$  ( $V$ = constant)

$\therefore P\alpha T$

When pressure is increased at constant volume, temperature also increases i.e. internal energy increases.

(b) In which part of the cycle heat is being given to the surrounding by the engine?

Ans: Heat is given out to the surrounding by the system in part CD. This case is the inverse of AB. In part CD, $dV = 0$, pressure decreases so temperature also decreases because $P\alpha T$, i.e. energy is given out by the system to the surrounding.

(c) What is the work done by the engine in one cycle? Write your answer in 

of \[{P_A}\], ${P_B}$, ${V_A}$.

Ans: Work done by system = $\int\limits_A^B {PdV}  + \int\limits_B^C {PdV}  + \int\limits_C^D {PdV}  + \int\limits_D^A {PdV} $ 

In A to B and C to D $dV = 0$ 

I.e., $\int\limits_A^B {PdV}  = 0$ and $\int\limits_C^D {PdV}  = 0$

For adiabatic change $P{V^\gamma } = K......\left( i \right)$ 

$ \Rightarrow P = \dfrac{K}{{{V^\gamma }}}$

$ \Rightarrow \int\limits_B^C {PdV}  = \int\limits_{{V_B}}^{{V_C}} {\dfrac{K}{{{V^\gamma }}}} dV$

$ \Rightarrow \int\limits_B^C {PdV}  = K\int\limits_{{V_B}}^{{V_C}} {{V^{ - \gamma }}} dV$

$ \Rightarrow \int\limits_B^C {PdV}  = K\left[ {\dfrac{{{V^{ - \gamma  + 1}}}}{{1 - \gamma }}} \right]_{{V_B}}^{{V_C}}$

\[ \Rightarrow \int\limits_B^C {PdV}  = \dfrac{K}{{1 - \gamma }}\left[ {V_C^{1 - \gamma } - V_B^{1 - \gamma }} \right]......\left( {ii} \right)\]

Similarly, D to A is also adiabatic so

$ \Rightarrow \int\limits_D^A {PdV}  = K\dfrac{{\left( {V_A^{1 - \gamma } - V_D^{1 - \gamma }} \right)}}{{1 - \gamma }}$ 

$ \Rightarrow \int\limits_D^A {PdV}  = \dfrac{{KV_A^{1 - \gamma } - KV_D^{1 - \gamma }}}{{1 - \gamma }}$

From $\left( i \right)$, we have $P{V^\gamma } = K$. Therefore, we get

$ \Rightarrow \int\limits_D^A {PdV}  = \dfrac{{{P_A}V_A^\gamma V_A^{1 - \gamma } - {P_D}V_D^\gamma V_D^{1 - \gamma }}}{{1 - \gamma }}$

$ \Rightarrow \int\limits_D^A {PdV}  = \dfrac{{{P_A}{V_A} - {P_D}{V_D}}}{{1 - \gamma }}$

Similarly,

$ \Rightarrow \int\limits_B^C {PdV}  = \dfrac{{{P_C}{V_C} - {P_B}{V_B}}}{{1 - \gamma }}$

Therefore, total work done = $0 + \dfrac{{{P_C}{V_C} - {P_B}{V_B}}}{{1 - \gamma }} + 0 + \dfrac{{{P_A}{V_A} - {P_D}{V_D}}}{{1 - \gamma }}$ 

$ \Rightarrow WD = \dfrac{1}{{1 - \gamma }}\left[ {{P_C}{V_C} - {P_B}{V_B} + {P_A}{V_A} - {P_D}{V_D}} \right]$ 

For adiabatic change, ${P_B}V_B^\gamma  = {P_C}V_C^\gamma $ 

$ \Rightarrow {P_C} = \dfrac{{{P_B}V_B^\gamma }}{{V_C^\gamma }}$

$ \Rightarrow {P_C} = {P_B}{\left( {\dfrac{{{V_B}}}{{{V_C}}}} \right)^\gamma }$

$ \Rightarrow {P_C} = {P_B}{\left( {\dfrac{{{V_B}}}{{2{V_B}}}} \right)^\gamma }$

$ \Rightarrow {P_C} = {P_B}\dfrac{1}{{{2^\gamma }}} = {P_B}{2^{ - \gamma }}$

Similarly,

$ \Rightarrow {P_D} = {P_A}{2^{ - \gamma }}$

Therefore, net $WD = \dfrac{1}{{1 - \gamma }}\left[ {{P_B}{V_C}{2^{ - \gamma }} - {P_B}{V_B} + {P_A}{V_A} - {P_A}{V_D}{2^{ - \gamma }}} \right]$

$ \Rightarrow WD = \dfrac{1}{{1 - \gamma }}\left[ {{P_B}2{V_B}{2^{ - \gamma }} - {P_B}{V_B} + {P_A}{V_A} - {P_A}2{V_A}{2^{ - \gamma }}} \right]$

$ \Rightarrow WD = \dfrac{1}{{1 - \gamma }}\left[ { - {P_B}{V_B}\left[ { - {2^{1 - \gamma }} + 1} \right] + {P_A}{V_A}\left[ {1 - {2^{1 - \gamma }}} \right]} \right]$

$ \Rightarrow WD = \dfrac{1}{{1 - \gamma }}\left[ { - {2^{1 - \gamma }} + 1} \right]\left[ { - {P_B}{V_B} + {P_A}{V_A}} \right]$

We have, $2{V_A} = 2{V_B}$ 

$ \Rightarrow {V_A} = {V_B}$

$ \Rightarrow WD = \dfrac{1}{{1 - \gamma }}\left[ { - {2^{1 - \gamma }} + 1} \right]\left[ { - {P_B}{V_A} + {P_A}{V_A}} \right]$

$ \Rightarrow WD = \dfrac{1}{{1 - \dfrac{5}{3}}}\left[ { - {2^{1 - \dfrac{5}{3}}} + 1} \right]\left[ { - {P_B} + {P_A}} \right]{V_A}$

$ \Rightarrow WD =  - \dfrac{3}{2}\left[ { - {2^{ - \dfrac{3}{2}}} + 1} \right]\left[ { - {P_B} + {P_A}} \right]{V_A}$

$ \Rightarrow WD = \dfrac{3}{2}\left[ {1 - {{\left( {\dfrac{1}{2}} \right)}^{\dfrac{2}{3}}}} \right]\left[ {{P_B} - {P_A}} \right]{V_A}$

(d) What is the efficiency of the engine?

\[\left[ {\gamma  = \dfrac{5}{3}{\text{ for the gas}}} \right]\], \[\left[ {{C_\upsilon } = \dfrac{3}{2}{\text{ for one mole}}} \right]\]

Ans: Heat $\left( Q \right)$ is supplied to the engine only during  $A \to B$. Therefore,

$ \Rightarrow Q = {Q_{AB}} = \Delta {U_{AB}} = n{C_V}\Delta T$ 

\[ \Rightarrow Q = \dfrac{3}{2}R\left( {{T_B} - {T_A}} \right)\]

We know that $PV = nRT$. Here, $n = 1$. Therefore, we get

\[ \Rightarrow Q = \dfrac{3}{2}\left( {{P_B}{V_B} - {P_A}{V_A}} \right)\]

We have, $2{V_A} = 2{V_B}$ 

$ \Rightarrow {V_A} = {V_B}$

\[ \Rightarrow Q = \dfrac{3}{2}\left( {{P_B}{V_A} - {P_A}{V_A}} \right)\]

\[ \Rightarrow Q = \dfrac{3}{2}\left( {{P_B} - {P_A}} \right){V_A}\]

Efficiency of the engine, $\eta  = \dfrac{W}{Q}$ 

$ \Rightarrow \eta  = \dfrac{{\dfrac{3}{2}\left[ {1 - {{\left( {\dfrac{1}{2}} \right)}^{\dfrac{2}{3}}}} \right]\left[ {{P_B} - {P_A}} \right]{V_A}}}{{\dfrac{3}{2}\left[ {{P_B} - {P_A}} \right]{V_A}}}$ 

$ \Rightarrow \eta  = \left[ {1 - {{\left( {\dfrac{1}{2}} \right)}^{\dfrac{2}{3}}}} \right]$

25. A cycle followed by an engine (made of one mole of an ideal gas in a cylinder with a piston) is shown in Figure. Find heat exchanged by the engine, with the surroundings for each section of the cycle. $\left( {{C_V} = \left( {\dfrac{3}{2}} \right)R} \right)$ 

(a) AB : constant volume

Ans: For $A \to B$, $dV = 0$ 

We know that, $dW = \int {P.dV} $ 

\[ \Rightarrow dW = \int {P.0} \]

\[ \Rightarrow dW = 0\]

By first law of thermodynamics, $dQ = dU + dW$

$ \Rightarrow dQ = dU + 0$

$ \Rightarrow dQ = dU$

We know that $dQ = n{C_V}dT$. Given that, $n = 1$ and ${C_V} = \left( {\dfrac{3}{2}} \right)R$. Therefore, we get

$ \Rightarrow dQ = 1 \times \left( {\dfrac{3}{2}} \right)R \times dT$

$ \Rightarrow dQ = 1 \times \left( {\dfrac{3}{2}} \right)R \times \left( {{T_B} - {T_A}} \right)$

$ \Rightarrow dQ = 1 \times \left( {\dfrac{3}{2}} \right)R \times \left( {{T_B} - {T_A}} \right)......\left( i \right)$

$ \Rightarrow dQ = \left( {\dfrac{3}{2}} \right)\left( {R{T_B} - R{T_A}} \right)$

$ \Rightarrow dQ = \left( {\dfrac{3}{2}} \right)\left( {{P_B}{V_B} - {P_A}{V_A}} \right)$

Hence, we get

$ \Rightarrow dU = dQ = \left( {\dfrac{3}{2}} \right)\left( {{P_B}{V_B} - {P_A}{V_A}} \right)$

Therefore, heat exchange to system,

$ \Rightarrow d{Q_1} = \left( {\dfrac{3}{2}} \right)\left( {{P_B}{V_B} - {P_A}{V_A}} \right)$

(b) BC : constant pressure

Ans: For $B \to C$, $\Delta P = 0$ and $n = 1$ 

$ \Rightarrow dQ = dU + dW$ 

$ \Rightarrow dQ = {C_V}\left( {dT} \right) + {P_B}dV$

$ \Rightarrow d{Q_2} = \left( {\dfrac{3}{2}} \right)R\left( {{T_C} - {T_B}} \right) + {P_B}\left( {{V_C} - {V_B}} \right)$

$ \Rightarrow d{Q_2} = \dfrac{3}{2}R{T_C} - \dfrac{3}{2}R{T_B} + {P_B}{V_C} - {P_B}{V_B}$

$ \Rightarrow d{Q_2} = \dfrac{3}{2}{P_C}{V_C} - \dfrac{3}{2}{P_B}{V_B} + {P_B}{V_C} - {P_B}{V_B}$

${V_A} = {V_B}$ and ${P_B} = {P_C}$ 

\[\therefore d{Q_2} = \dfrac{3}{2}{P_B}{V_C} - \dfrac{3}{2}{P_B}{V_A} + {P_B}{V_C} - {P_B}{V_A}\]

\[ \Rightarrow d{Q_2} = \dfrac{5}{2}{P_B}{V_C} - \dfrac{5}{2}{P_B}{V_A}\]

\[\therefore d{Q_2} = \dfrac{5}{2}{P_B}\left( {{V_C} - {V_A}} \right)\]

(c) CD : adiabatic

Ans: For $C \to D$, adiabatic change

\[\therefore dQ = 0\] (No exchange of heat)

(d) DA : constant pressure

Ans: For $D \to A$, $\Delta P = 0$

Compression of gas from volume ${V_D}$ to ${V_A}$ at constant pressure. Therefore, heat exchange is similar to part (b).

\[\therefore d{Q_3} = \dfrac{5}{2}{P_A}\left( {{V_A} - {V_D}} \right)\]

26. Consider that an ideal gas ($n$ moles) is expanding in a process given by $P = f\left( V \right)$, which passes through a point $\left( {{V_0},{P_0}} \right)$. Show that the gas is absorbing heat at $\left( {{P_0},{V_0}} \right)$ if the slope of the curve $P = f\left( V \right)$ is larger than the slope of the adiabat passing through $\left( {{P_0},{V_0}} \right)$. 

Ans: Slope of the graph at $\left( {{V_0},{P_0}} \right)$ = ${\left( {\dfrac{{dP}}{{dV}}} \right)_{\left( {{V_0},{P_0}} \right)}}$ 

We know that for adiabatic process $P{V^\gamma } = K$

$ \Rightarrow P = \dfrac{K}{{{V^\gamma }}}$

$ \Rightarrow \dfrac{{dP}}{{dV}} = K\left( { - \gamma } \right){V^{ - \gamma  - 1}}$

$ \Rightarrow \dfrac{{dP}}{{dV}} =  - \gamma P{V^\gamma }{V^{ - \gamma }}{V^{ - 1}}$

$ \Rightarrow \dfrac{{dP}}{{dV}} = \dfrac{{ - \gamma P}}{V}$

$ \Rightarrow {\left( {\dfrac{{dP}}{{dV}}} \right)_{\left( {{V_0},{P_0}} \right)}} = \dfrac{{ - \gamma {P_0}}}{{{V_0}}}$

Now, heat absorbed in the process $P = f\left( V \right)$,

$\therefore dQ = dU + dW$ 

\[ \Rightarrow dQ = n{C_V}dT + PdV.....\left( i \right)\]

We know that $PV = nRT$. Therefore, we get

$ \Rightarrow T = \dfrac{{PV}}{{nR}}$ 

$ \Rightarrow T = \dfrac{V}{{nR}}f\left( V \right)$ (Given, $P = f\left( V \right)$ )

$ \Rightarrow \dfrac{{dT}}{{dV}} = \dfrac{1}{{nR}}\left[ {f\left( V \right) + Vf'\left( V \right)} \right]$

Now, continue solving equation $\left( i \right)$ 

\[ \Rightarrow \dfrac{{dQ}}{{dV}} = n{C_V}\dfrac{{dT}}{{dV}} + P\dfrac{{dV}}{{dV}}\]

\[ \Rightarrow \dfrac{{dQ}}{{dV}} = \dfrac{{n{C_V}}}{{nR}}\left[ {f\left( V \right) + Vf'\left( V \right)} \right] + P\]

\[ \Rightarrow {\left( {\dfrac{{dQ}}{{dV}}} \right)_{V = {V_0}}} = \dfrac{{{C_V}}}{R}\left[ {f\left( {{V_0}} \right) + {V_0}f'\left( {{V_0}} \right)} \right] + f\left( {{V_0}} \right)\]

\[ \Rightarrow {\left( {\dfrac{{dQ}}{{dV}}} \right)_{V = {V_0}}} = f\left( {{V_0}} \right)\left[ {\dfrac{{{C_V}}}{R} + 1} \right] + {V_0}f'\left( {{V_0}} \right)\dfrac{{{C_V}}}{R}\]

We know that ${C_P} - {C_V} = R$

$ \Rightarrow \dfrac{{{C_P}}}{{{C_V}}} - 1 = \dfrac{R}{{{C_V}}}$

$ \Rightarrow \gamma  - 1 = \dfrac{R}{{{C_V}}}$

$ \Rightarrow {C_V} = \dfrac{R}{{\gamma  - 1}}$

$ \Rightarrow \dfrac{{{C_V}}}{R} = \dfrac{1}{{\gamma  - 1}}$

\[ \Rightarrow {\left( {\dfrac{{dQ}}{{dV}}} \right)_{V = {V_0}}} = f\left( {{V_0}} \right)\left[ {\dfrac{1}{{\gamma  - 1}} + 1} \right] + {V_0}f'\left( {{V_0}} \right)\dfrac{1}{{\gamma  - 1}}\]

\[ \Rightarrow {\left( {\dfrac{{dQ}}{{dV}}} \right)_{V = {V_0}}} = f\left( {{V_0}} \right)\left[ {\dfrac{{1 + \gamma  - 1}}{{\gamma  - 1}}} \right] + \dfrac{{{V_0}f'\left( {{V_0}} \right)}}{{\gamma  - 1}}\]

\[ \Rightarrow {\left( {\dfrac{{dQ}}{{dV}}} \right)_{V = {V_0}}} = \dfrac{\gamma }{{\left( {\gamma  - 1} \right)}}f\left( {{V_0}} \right) + {V_0}\dfrac{{f'\left( {{V_0}} \right)}}{{\gamma  - 1}}\]

\[ \Rightarrow {\left( {\dfrac{{dQ}}{{dV}}} \right)_{V = {V_0}}} = \dfrac{1}{{\left( {\gamma  - 1} \right)}}\left[ {\gamma f\left( {{V_0}} \right) + {V_0}f'\left( {{V_0}} \right)} \right]\]

\[ \Rightarrow {\left( {\dfrac{{dQ}}{{dV}}} \right)_{V = {V_0}}} = \dfrac{1}{{\left( {\gamma  - 1} \right)}}\left[ {\gamma {P_0} + {V_0}f'\left( {{V_0}} \right)} \right]\] ( $\because f\left( {{V_0}} \right) = {P_0}$ )

If $\gamma  > 1$,so $\left( {\dfrac{1}{{\gamma  - 1}}} \right)$ is positive.

Then, heat is absorbed where \[{\left( {\dfrac{{dQ}}{{dV}}} \right)_{V = {V_0}}} > 0\] when gas expands.

Hence, \[\gamma {P_0} + {V_0}f'\left( {{V_0}} \right) > 0\] 

$ \Rightarrow {V_0}f'\left( {{V_0}} \right) > \left( { - \gamma {P_0}} \right)$ 

$ \Rightarrow f'\left( {{V_0}} \right) > \left( {\dfrac{{ - \gamma {P_0}}}{{{V_0}}}} \right)$

27. Consider one mole of perfect gas in a cylinder of unit cross section with a piston attached. A spring (spring constant $k$ ) is attached (unstretched length $L$ ) to the piston and to the bottom of the cylinder. Initially the spring is unstretched and the gas is in equilibrium. A certain amount of heat $Q$ is supplied to the gas causing an increase of volume from ${V_0}$ to ${V_1}$.

(a) What is the initial pressure of the system?

Ans: It is considered that piston mass is less. Piston is balanced by atmospheric pressure ${P_a}$.

Thus, initial pressure of the system = ${P_a}$

(b) What is the final pressure of the system?

Ans: On supply of heat $Q$, volume of gas increases from ${V_0}$ to ${V_1}$ and spring gets stretched also.

Therefore, increase in volume = ${V_1} - {V_0}$ 

Let $x$ be the displacement of piston, then volume increase in cylinder 

= Area of base × height

$ = A \times x$ 

$ \Rightarrow A \times x = {V_1} - {V_0}$

$\therefore x = \dfrac{{{V_1} - {V_0}}}{A}$

Force exerted by spring ${F_S} = Kx = \dfrac{{K\left( {{V_1} - {V_0}} \right)}}{A}$ 

Given that, the cylinder is of unit cross section area. Therefore, $A = 1$ 

$ \Rightarrow {F_S} = K\left( {{V_1} - {V_0}} \right)$

Final total pressure on gas ${P_f} = {P_a} + K\left( {{V_1} - {V_0}} \right)$ 

(c) Using the first law of thermodynamics, write down a relation between $Q$, ${P_a}$, $V$, ${V_0}$ and $k$.

Ans: By first law of thermodynamics, $dQ = dU + dW$ 

$dU = {C_V}\left( {T - {T_0}} \right)$ 

$T$ is final temperature of gas

${T_0}$ is initial temperature of gas

$n = 1$ 

$\therefore T = \dfrac{{{P_f}{V_f}}}{R} = \dfrac{{{P_a} + K\left( {{V_1} - {V_0}} \right){V_1}}}{R}$ 

Work done = $P.dV$ + increase in potential energy of spring

$ \Rightarrow dW = {P_a}\left( {{V_1} - {V_0}} \right) + \dfrac{1}{2}k{x^2}$ 

Now, $dQ = dU + dW$

$ \Rightarrow dQ = {C_V}\left( {T - {T_0}} \right) + {P_a}\left( {{V_1} - {V_0}} \right) + \dfrac{1}{2}k{x^2}$

$\therefore dQ = {C_V}\left( {T - {T_0}} \right) + {P_a}\left( {{V_1} - {V_0}} \right) + \dfrac{1}{2}k{\left( {{V_1} - {V_0}} \right)^2}$

This is our required equation.

Benefits of Referring to Solution Books

• Since the concept of Thermodynamics may seem to be difficult to understand, the students might need a guidebook that explains the significance of these laws and their applications in our day-to-day lives. The NCERT Exemplar Solutions books include just the right amount of explanation and step-by-step analysis of the formulation of these laws.

• The questions that are of prime importance are also included in the practice set. 

• It is important for the students to learn the concepts at first before they start solving the questions. But, since it is the world of competition, they need to focus on repairing strategically so that they can score more in the Examination. 

• For that, getting familiarised with the pattern of questions and the mark division for each and every question is also very important. Consulting these books will immensely help them to get an idea of what kind of questions can be there in their question papers.

• The concept is very new to the students and they may face some kind of difficulties while answering the questions. The solutions provided in the books will help them to re-verify their answers and will also explain why they need to follow a certain method while answering.

• Due to this pandemic, the students cannot directly communicate with the trainers and their mentors. The solutions will help them to get prepared for their Examinations as they are solved by efficient trainers.