
Let $f:R \to R$ be a function defined by $f(x) = \left\{ k - 2x,{\text{ if }}x \leqslant - 1 \\
2x + 3,{\text{ if }}x > - 1 \\
\right.$ , of $f$has a local minimum at $x = - 1$, then possible values of $k$is.
A. $1$
B. $0$
C. $ - \dfrac{1}{2}$
D. $ - 1$
Answer
232.8k+ views
Hint: Here, we have to find out the possible values of $k$. In this question we, have to take limits to find out the value of $k$. Firstly, we take the function $f(x) > - 1$ and take the limit of this function and find out the $f(x)$.
Secondly, we take the function $f(x) \leqslant - 1$and take a limit of the function and calculate the value of $f(x)$in terms of $k$.We are given the local minimum at $x = - 1$.Now these three conditions and find the value of .
Complete step by step solution:
We have;
$f(x) = \left\{
k - 2x,{\text{ if }}x \leqslant - 1 \\
2x + 3,{\text{ if }}x > - 1 \\
\right.$
Let us take the limit of a function $f(x) > - 1$ we get;
$
\mathop {\lim }\limits_{x \to - {1^ + }} f(x) = \mathop {\lim }\limits_{x \to - {1^ + }} (2x + 3) \\
\Rightarrow \mathop {\lim }\limits_{x \to - {1^ + }} f(x) = 2( - 1) + 3 \\
\Rightarrow \mathop {\lim }\limits_{x \to - {1^ + }} f(x) = - 2 + 3 \\
\Rightarrow \mathop {\lim }\limits_{x \to - {1^ + }} f(x) = + 1 \\
$
Similarly, take the function with limit $f(x) \leqslant - 1$ we have,
$
\mathop {\lim }\limits_{x \to - {1^ - }} f(x) = \mathop {\lim }\limits_{x \to - {1^ - }} (k - 2x) \\
\Rightarrow \mathop {\lim }\limits_{x \to - {1^ - }} f(x) = k - 2( - 1) \\
\Rightarrow \mathop {\lim }\limits_{x \to - {1^ - }} f(x) = k + 2 \\
$
Here we are having the local minimum of function $f(x)$at $x = - 1$.
Therefore, we can write the function as follows:
$f( - {1^ + }) \geqslant f( - 1) \geqslant f( - {1^ - })$
Putting all the values we get;
$1 \geqslant k + 2$
Subtract from both sides we get;
$
1 - 2 \geqslant k + 2 - 2 \\
\Rightarrow - 1 \geqslant k \\
\Rightarrow k \leqslant - 1 \\
$
Therefore, according to the local minimum of the function, we can take the possible value of $k$ is taken as$ - 1$.
Option ‘D’ is correct
Note: In this type of question, we must consider the conditions for each function we have given, and we must determine the limit of the given variable based on the conditions. Always keep an eye out for signs of inequity in the questions, such as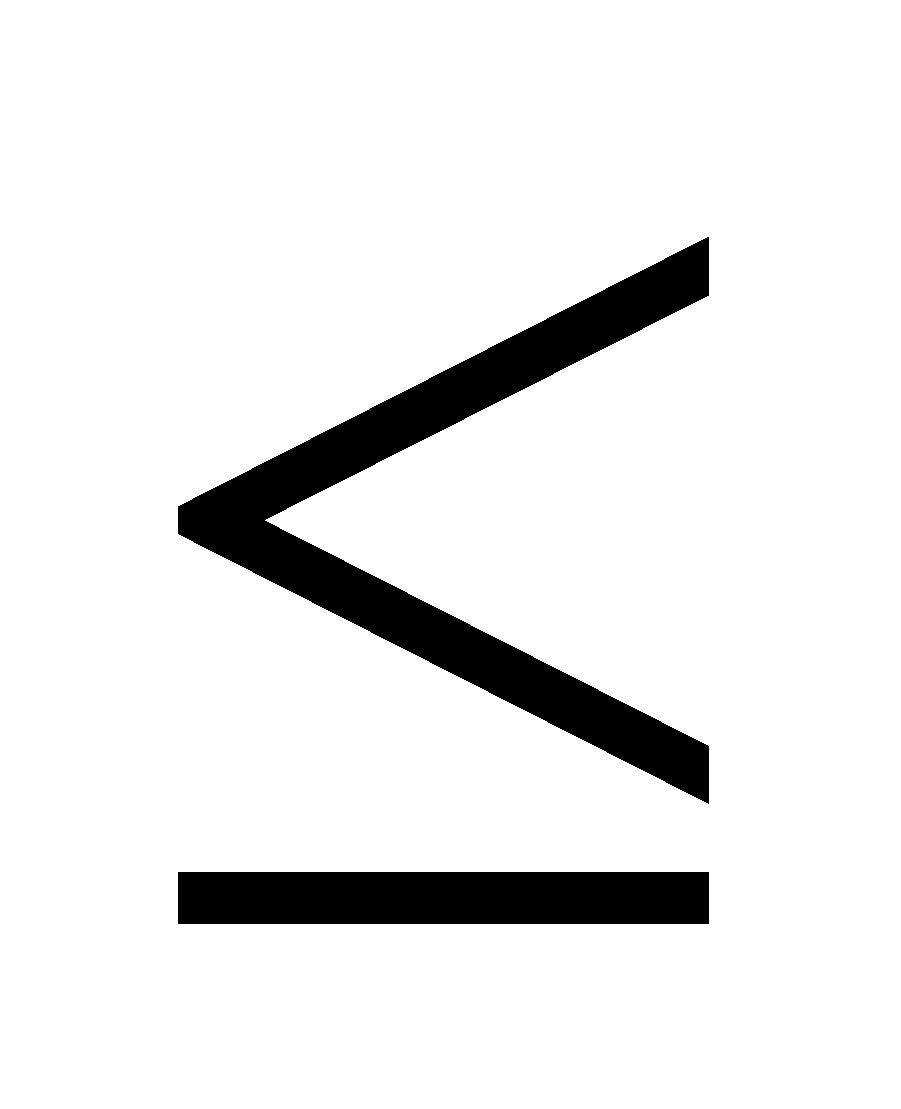 (less than equal to),
(less than equal to),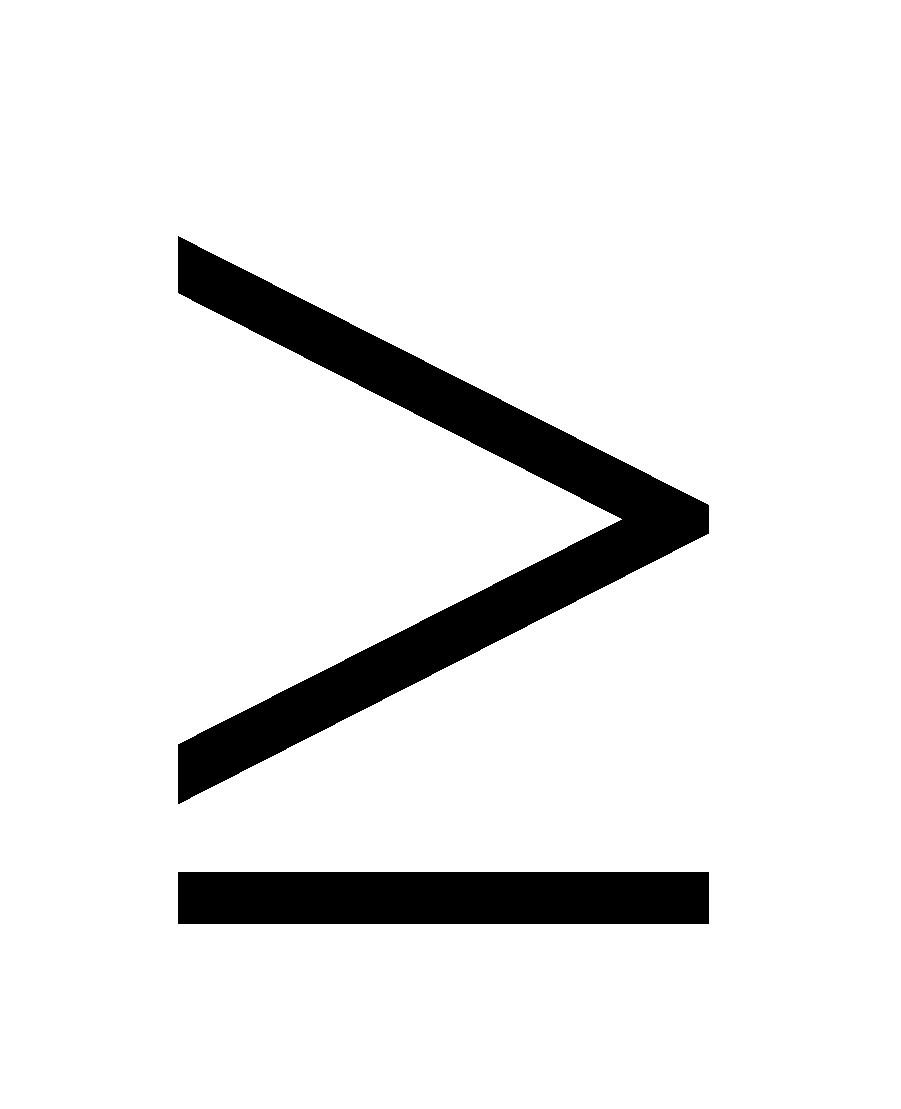 (greater than equal to),
(greater than equal to), (less than),
(less than),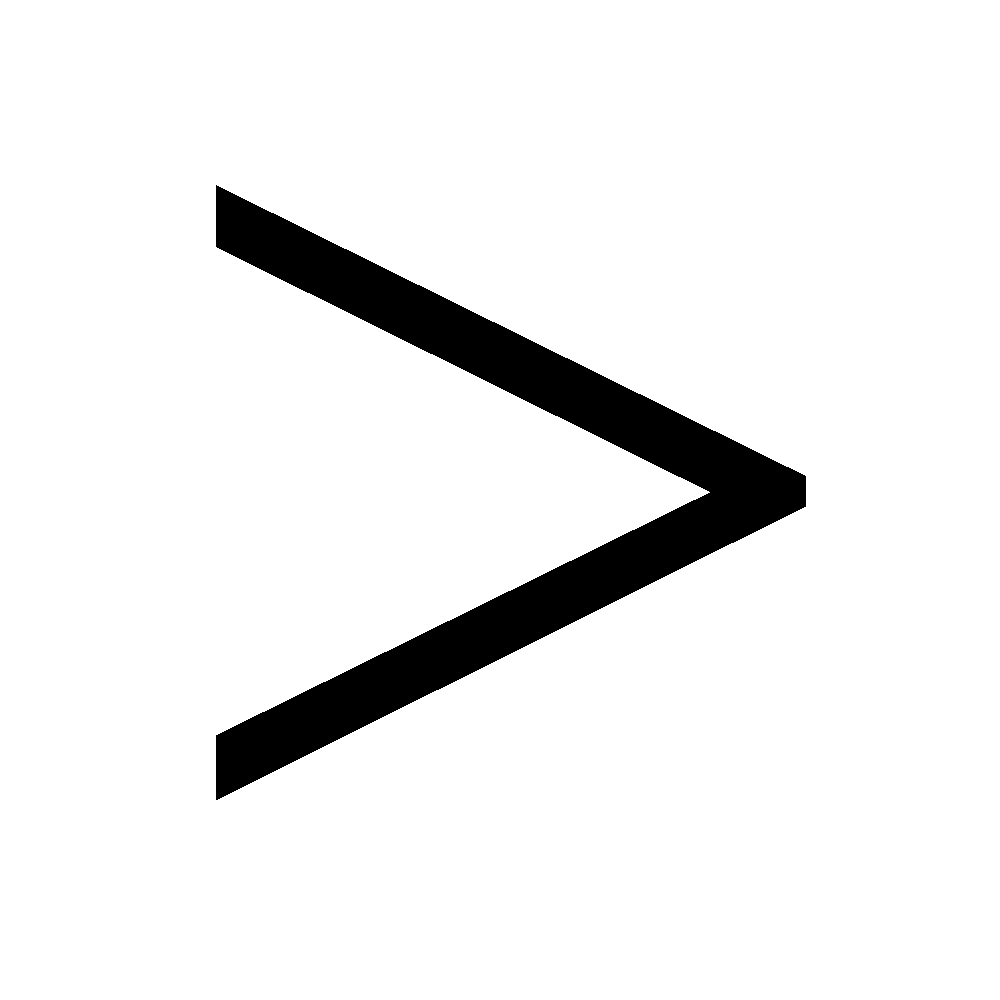 and (greater than). If we took 'x' conditions in a function. Always solve inequalities by adding, subtracting, multiplying, or dividing both sides until the variable is left alone. Do not attempt to solve it directly.
and (greater than). If we took 'x' conditions in a function. Always solve inequalities by adding, subtracting, multiplying, or dividing both sides until the variable is left alone. Do not attempt to solve it directly.
Secondly, we take the function $f(x) \leqslant - 1$and take a limit of the function and calculate the value of $f(x)$in terms of $k$.We are given the local minimum at $x = - 1$.Now these three conditions and find the value of .
Complete step by step solution:
We have;
$f(x) = \left\{
k - 2x,{\text{ if }}x \leqslant - 1 \\
2x + 3,{\text{ if }}x > - 1 \\
\right.$
Let us take the limit of a function $f(x) > - 1$ we get;
$
\mathop {\lim }\limits_{x \to - {1^ + }} f(x) = \mathop {\lim }\limits_{x \to - {1^ + }} (2x + 3) \\
\Rightarrow \mathop {\lim }\limits_{x \to - {1^ + }} f(x) = 2( - 1) + 3 \\
\Rightarrow \mathop {\lim }\limits_{x \to - {1^ + }} f(x) = - 2 + 3 \\
\Rightarrow \mathop {\lim }\limits_{x \to - {1^ + }} f(x) = + 1 \\
$
Similarly, take the function with limit $f(x) \leqslant - 1$ we have,
$
\mathop {\lim }\limits_{x \to - {1^ - }} f(x) = \mathop {\lim }\limits_{x \to - {1^ - }} (k - 2x) \\
\Rightarrow \mathop {\lim }\limits_{x \to - {1^ - }} f(x) = k - 2( - 1) \\
\Rightarrow \mathop {\lim }\limits_{x \to - {1^ - }} f(x) = k + 2 \\
$
Here we are having the local minimum of function $f(x)$at $x = - 1$.
Therefore, we can write the function as follows:
$f( - {1^ + }) \geqslant f( - 1) \geqslant f( - {1^ - })$
Putting all the values we get;
$1 \geqslant k + 2$
Subtract from both sides we get;
$
1 - 2 \geqslant k + 2 - 2 \\
\Rightarrow - 1 \geqslant k \\
\Rightarrow k \leqslant - 1 \\
$
Therefore, according to the local minimum of the function, we can take the possible value of $k$ is taken as$ - 1$.
Option ‘D’ is correct
Note: In this type of question, we must consider the conditions for each function we have given, and we must determine the limit of the given variable based on the conditions. Always keep an eye out for signs of inequity in the questions, such as
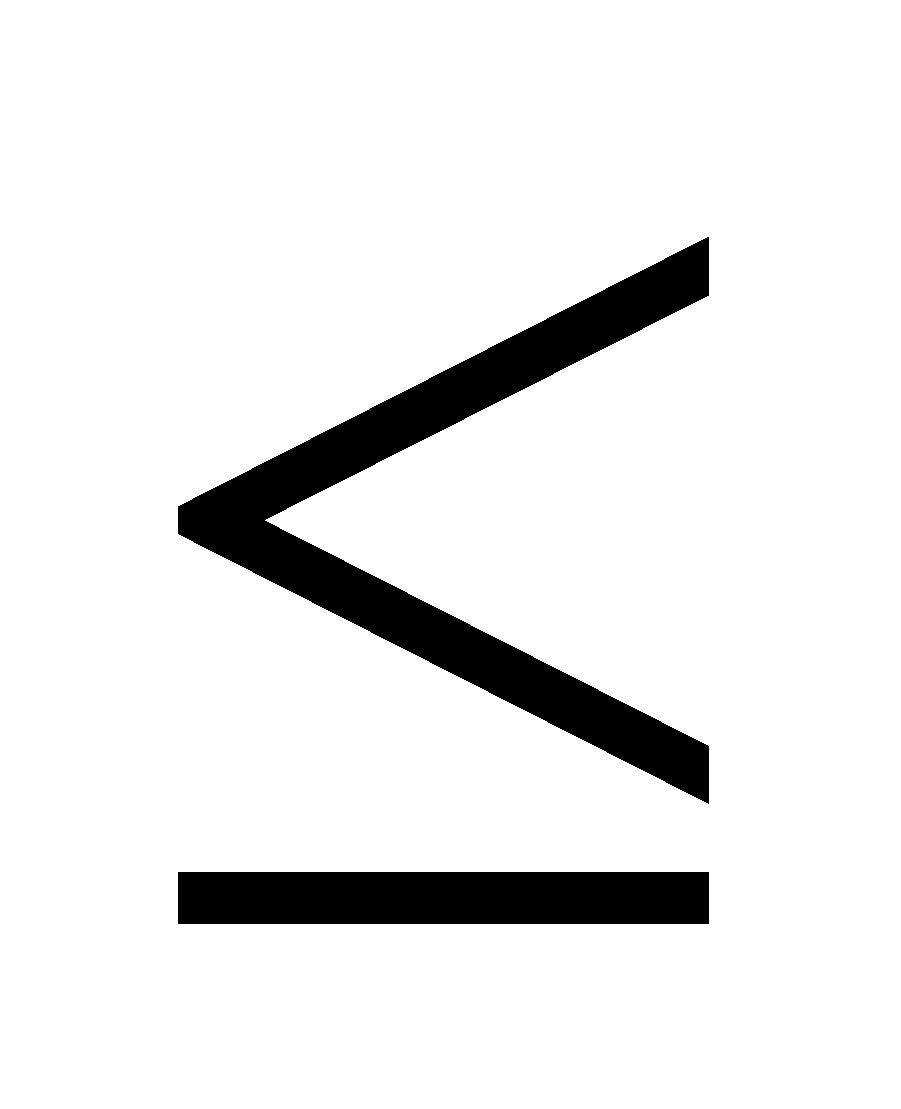 (less than equal to),
(less than equal to), (greater than equal to),
(greater than equal to), (less than),
(less than), and (greater than). If we took 'x' conditions in a function. Always solve inequalities by adding, subtracting, multiplying, or dividing both sides until the variable is left alone. Do not attempt to solve it directly.
and (greater than). If we took 'x' conditions in a function. Always solve inequalities by adding, subtracting, multiplying, or dividing both sides until the variable is left alone. Do not attempt to solve it directly.Recently Updated Pages
Alpha, Beta, and Gamma Decay Explained

Atomic Structure Explained: Key Concepts for Students

Collision: Meaning, Types & Real-Life Examples

Elastic Collisions in One Dimension Explained

Ideal and Non-Ideal Solutions: Differences, Examples & Table

Average and RMS Value Explained: Formulas & Examples

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

JEE Main Marking Scheme 2026- Paper-Wise Marks Distribution and Negative Marking Details

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Understanding the Electric Field of a Uniformly Charged Ring

Derivation of Equation of Trajectory Explained for Students

Understanding Electromagnetic Waves and Their Importance

Inductive Effect and Its Role in Acidic Strength

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry




