




How to Calculate Average and RMS Value with Simple Examples
Average and RMS (Root Mean Square) values are essential concepts in the analysis of alternating current (AC) waveforms. They allow precise measurement of the effective value and average behavior of time-varying currents and voltages, which is critical for both theoretical and applied physics, especially in AC circuit study for JEE Main.
Definition and Physical Meaning of Average and RMS Values
The average value of an alternating quantity represents the arithmetic mean of all its instantaneous values over a specified period, typically a half-cycle for symmetric waveforms, as the average over a full cycle becomes zero due to symmetry.
The RMS value quantifies the equivalent direct current (DC) or voltage that would produce the same amount of heat energy in a resistor as the actual AC does over one complete cycle. It is key for determining the effective power delivered by AC sources.
Mathematical Formulation and Common Waveforms
For a time-varying current $I(t)$ with period $T$, the average and RMS values are given by:
Average value: $I_{\text{avg}} = \dfrac{1}{T} \int_0^T I(t) \, dt$
RMS value: $I_{\text{rms}} = \sqrt{ \dfrac{1}{T} \int_0^T [I(t)]^2 \, dt }$
For symmetric AC waveforms like sine and triangular waves, the average is calculated over a half-cycle. For full-wave rectified signals and square waves, the calculations differ due to waveform properties.
Average and RMS Value for Standard AC Waveforms
For sinusoidal currents or voltages of the form $I(t) = I_0 \sin \omega t$:
Average value (half-cycle): $I_{\text{avg}} = \dfrac{2I_0}{\pi}$
RMS value (full cycle): $I_{\text{rms}} = \dfrac{I_0}{\sqrt{2}}$
For a square wave of peak value $I_0$, both average and RMS values are $I_0$. Rectifier circuits and triangular waves have characteristic calculations based on their waveform shapes.
For detailed study on average values in varied contexts, refer to Average Velocity Formula.
Derivation: Sine Wave Average and RMS Values
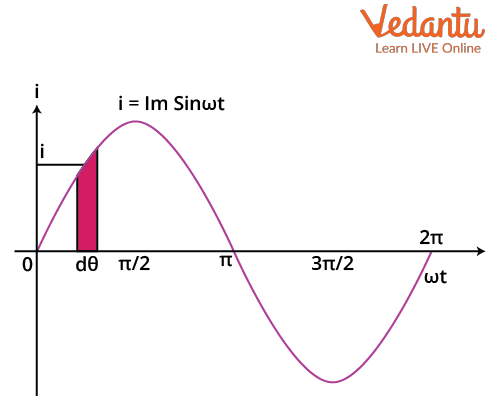
Consider a sinusoidal current: $I = I_0 \sin \omega t$. The average value over one half-cycle ($0$ to $\pi$) is:
$I_{\text{avg}} = \dfrac{1}{\pi} \int_0^{\pi} I_0 \sin \theta \, d\theta = \dfrac{2 I_0}{\pi}$
The RMS value over one complete cycle is:
$I_{\text{rms}} = \sqrt{\dfrac{1}{2\pi} \int_0^{2\pi} I_0^2 \sin^2 \theta \, d\theta} = \dfrac{I_0}{\sqrt{2}}$
Average and RMS Values in Rectifier Circuits
Rectifiers convert alternating to unidirectional current. For a half-wave rectifier, the average and RMS currents are $I_{\text{avg}} = \dfrac{I_0}{\pi}$ and $I_{\text{rms}} = \dfrac{I_0}{2}$, respectively. For a full-wave rectifier, these become $I_{\text{avg}} = \dfrac{2I_0}{\pi}$ and $I_{\text{rms}} = \dfrac{I_0}{\sqrt{2}}$.
Rectified signals are vital in practical circuits where only one current direction is desired. Understanding these values facilitates solving questions about heating effects and average DC output.
Further insight into power calculations can be explored at Work, Energy and Power.
Key Formulas for Average and RMS Values
| Waveform | Average / RMS Value |
|---|---|
| Sine wave | $I_{\text{avg}} = 0.637 I_0$, $I_{\text{rms}} = 0.707 I_0$ |
| Half-wave rectified sine | $I_{\text{avg}} = 0.318 I_0$, $I_{\text{rms}} = 0.5 I_0$ |
| Full-wave rectified sine | $I_{\text{avg}} = 0.637 I_0$, $I_{\text{rms}} = 0.707 I_0$ |
| Square wave | $I_{\text{avg}} = I_0$, $I_{\text{rms}} = I_0$ |
| Triangular wave | $I_{\text{avg}} = I_0$, $I_{\text{rms}} = \dfrac{I_0}{\sqrt{3}}$ |
Applications and Significance in Physics
The average value is significant for rectifiers and circuits where the mean output matters. RMS values are used for calculating the heating effect, power delivered, and to specify ratings of electrical devices, such as the 230 V AC household supply, which refers to RMS value.
Instrument readings, such as moving coil meters, use RMS values since they relate to the actual ability of an AC signal to do work over time.
Solving Problems Involving Average and RMS Values
To solve problems involving effective value or power, RMS values must be used, especially for heating or electrical energy calculations. Average values are more relevant for computing net flow or rectified outputs.
For example, a 10 A peak sine current has $I_{\text{avg}} = 6.37$ A and $I_{\text{rms}} = 7.07$ A. Always match the requirement of the question to the correct value type.
Further concepts on force averages are available at Average Force Formula.
Key Differences: Average Value vs. RMS Value
| Characteristic | Average Value vs. RMS Value |
|---|---|
| Physical meaning | Average gives mean output; RMS gives effective DC |
| Full-cycle symmetry | Average over full cycle is zero for pure sine |
| Use in power calculation | RMS alone is used for power/heating effects |
| Application | Average for rectifiers; RMS for AC ratings |
| Numeric relation (sine) | RMS = 1.11 × Average for sine waves |
Form Factor and Ratio of RMS to Average Value
The form factor, defined as the ratio of RMS value to average value, is significant in waveform analysis. For a sine wave, it is 1.11, indicating $I_{\text{rms}}$ is 11% higher than $I_{\text{avg}}$.
For square waves, the form factor is 1.0. For half-wave rectified sine, it is approximately 1.57. This concept assists in rapid calculation and comparison of signal effectiveness.
Typical JEE Mistakes and Important Points
- RMS value is always used for power and heating calculations
- Avoid using average over a full cycle for AC; it is zero
- Do not mix up peak, average, and RMS values
- For rectifiers, choose formulas as per half-wave or full-wave specification
- Carefully convert between SI units of ampere and volt
- Always reference correct form factor for waveform type
Further Context and Related Concepts
The concept of RMS and average values extends to alternating voltage, current, and even non-electrical waveforms such as those seen in mechanical oscillations. Deeper understanding of these principles assists in analyzing energy, power, and response in various physical systems.
To reinforce the principles of energy associated with these values, see Understanding Energy.
A clear grasp of waveform analysis, including average and RMS calculations, strengthens preparation for advanced topics, such as electromagnetic induction and AC circuit response. For foundational ideas on mirror reflections related to wave motion, refer to Velocity of Image in Plane Mirror.
Potential energy concepts relevant to oscillating systems align with average and RMS understanding. For more, visit Elastic Potential Energy.
FAQs on Understanding Average and RMS Value in Electrical Circuits
1. What is the average value of an alternating current (AC)?
The average value of an AC waveform is the average of all instantaneous values of current (or voltage) over one half-cycle.
Key points:
- For a pure sinusoidal AC, Average Value = (2/π) × Maximum Value (Im)
- Represents the equivalent steady DC value in half a cycle
- For full cycle, the average value is zero (due to symmetry)
2. What is the RMS value in AC circuits?
The RMS (Root Mean Square) value of an alternating current represents the effective value, producing the same heating effect as a corresponding DC value.
Important points:
- RMS Value = 0.707 × Maximum Value (Im) for a sinusoidal current
- Also called the effective or virtual value
- Used in electrical ratings and calculations
3. How do you calculate the average value of a sinusoidal current?
To calculate the average value of a sinusoidal alternating current, use the formula:
- Average value = (2/π) × Maximum current (Im)
- Formula: Iavg = (2/π) × Im
- Applies only over one half-cycle for pure sine waves
4. What is the relation between average value and RMS value?
The RMS value of AC is always greater than its average value in a sinusoidal waveform.
Relation:
- RMS Value ≈ 1.11 × Average Value for sine waves
- RMS expresses the effective or heating value, average gives mean over half-cycle
5. Why is the RMS value important in electrical engineering?
RMS value is important because it measures the effective power of alternating current, essential for sizing electrical components.
Applications include:
- Rating household electrical appliances (like bulbs)
- Calculating power consumption
- Ensuring safety and efficiency in circuit design
6. Explain the significance of average value in AC analysis.
The average value in AC analysis helps determine the direct equivalent value of AC for one half-cycle.
- Used in designing rectifiers and analyzing half-wave circuits
- Helps to compare AC with DC values
7. What is the formula for RMS value of a sinusoidal alternating current?
The formula for RMS value of a sinusoidal AC is:
- Irms = (Im)/√2 = 0.707 × Im
- Im = maximum (peak) value of current
- This value gives equivalent DC for same power dissipation
8. What is the average and rms value of a symmetrical square wave?
For a symmetrical square wave of amplitude Im:
- Average value = Im
- RMS value = Im
- Both values are equal, as the waveform maintains constant amplitude
9. What is the physical meaning of RMS and average values for AC?
RMS value describes the heating/effective value of AC, while average value reflects the mean over a half-cycle.
- RMS: Actual work/power equivalence to DC
- Average: DC value producing same net charge transfer over half-cycle
10. How do average and RMS values affect power calculation in AC circuits?
Power calculation in AC circuits uses the RMS value, not the average value.
- Active power (P) = VRMS × IRMS × cos(ϕ)
- Using average value would underestimate real power
11. What is the RMS value of a half-wave rectified sine wave?
The RMS value for a half-wave rectified sine wave is:
- Irms = Im/2
- Im = maximum value of input current
- Less than full sine wave due to missing negative half
12. Why is the average value of AC over a full cycle zero?
The average value of AC over a full cycle is zero because the positive and negative halves cancel out.
- This reflects the symmetry of sinusoidal waves
- Only half-cycle is used for practical average calculations


































