
If a triangle \[ABC\] has vertices \[A\left( { - 1,7} \right)\], \[B\left( { - 7,1} \right)\], and \[C\left( {5, - 5} \right)\]. What is the coordinate orthocentre of the triangle?
A. (-3,3)
B. \[\left( { - \dfrac{3}{5},\dfrac{3}{5}} \right)\]
C. \[\left( {\dfrac{3}{5}, - \dfrac{3}{5}} \right)\]
D. (3,-3)
Answer
232.8k+ views
Hint We will apply the formula of the product of slopes of perpendicular lines to find the equation line perpendicular to \[BC\] and passes through the point \[A\]. Again, we will apply the formula of the product of slopes of perpendicular lines to find the equation line perpendicular to \[AC\] and passes through the point \[B\]. The intersection point of the lines is the orthocentre of triangle \[ABC\].
Formula used
The product of slopes of two perpendicular lines is -1.
The formula for the slope of the line passes through the points \[\left( {{x_1},{y_1}} \right)\] and \[\left( {{x_2},{y_2}} \right)\] is \[\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\].
Complete step by step solution:
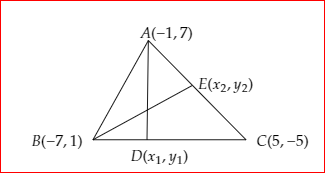
Image: Triangle \[ABC\]
Let \[D\left( {{x_1},{y_1}} \right)\] be a point on \[BC\] and \[AD\] is perpendicular to \[BC\].
Let \[E\left( {{x_2},{y_2}} \right)\] be a point on \[AC\] and \[BE\] is perpendicular to \[AC\].
Now we will find the slopes of \[BC\], \[AD\], \[BE\], and \[AC\].
The slope of the line \[BC\] is \[\dfrac{{ - 5 - 1}}{{5 + 7}} = \dfrac{{ - 6}}{{12}} = - \dfrac{1}{2}\].
The slope of the line \[AD\] is \[\dfrac{{{y_1} - 7}}{{{x_1} + 1}}\].
The slope of the line \[AC\] is \[\dfrac{{ - 5 - 7}}{{5 + 1}} = \dfrac{{ - 12}}{6} = - 2\].
The slope of the line \[AD\] is \[\dfrac{{{y_2} - 1}}{{{x_2} + 7}}\].
Since \[AD\] is perpendicular to \[BC\].
\[\dfrac{{{y_1} - 7}}{{{x_1} + 1}} \cdot \left( { - \dfrac{1}{2}} \right) = - 1\]
\[ \Rightarrow {y_1} - 7 = 2\left( {{x_1} + 1} \right)\]
Replace \[{x_1}\] by \[x\] and \[{y_1}\] by \[y\] to find the equation \[AD\]
\[ \Rightarrow y - 7 = 2\left( {x + 1} \right)\]
\[ \Rightarrow y - 7 = 2x + 2\]
\[ \Rightarrow 2x - y + 9 = 0\] ….(i)
Since \[BE\] is perpendicular to \[AC\].
\[\dfrac{{{y_2} - 1}}{{{x_2} + 7}} \cdot \left( { - 2} \right) = - 1\]
\[ \Rightarrow 2\left( {{y_2} - 1} \right) = \left( {{x_2} + 7} \right)\]
Replace \[{x_2}\] by \[x\] and \[{y_2}\] by \[y\] to find the equation \[AD\]
\[ \Rightarrow 2\left( {y - 1} \right) = x + 7\]
\[ \Rightarrow 2y - 2 = x + 7\]
\[ \Rightarrow x - 2y + 9 = 0\] ….(ii)
Now multiply 2 with equation (ii) and subtract (i) from it
\[2x - 4y + 18 = 0\]
\[2x - y + 9 = 0\]
\[\overline {\,\,\,\, - 3y + 9 = 0} \]
\[ \Rightarrow 3y = 9\]
\[ \Rightarrow y = 3\]
Substitute \[y = 3\] in equation (i)
\[2x - 3 + 9 = 0\]
\[ \Rightarrow 2x = - 6\]
\[ \Rightarrow x = - 3\]
The coordinate of the orthocentre is \[\left( { - 3,3} \right)\]
Hence option A is the correct option.
Note: An orthocentre is a point that is an intersection point of perpendicular lines which are drawn from a vertex to the opposite side.
Sometimes students take midpoint of \[BC\] to calculate perpendicular line on \[BC\] through the vertex \[A\]. This is an incorrect way. The perpendicular line may not pass through the midpoint. Thus we will assume the coordinate of point \[D\] and \[E\] on the lines \[BC\] and \[AC\] respectively.
Formula used
The product of slopes of two perpendicular lines is -1.
The formula for the slope of the line passes through the points \[\left( {{x_1},{y_1}} \right)\] and \[\left( {{x_2},{y_2}} \right)\] is \[\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\].
Complete step by step solution:

Image: Triangle \[ABC\]
Let \[D\left( {{x_1},{y_1}} \right)\] be a point on \[BC\] and \[AD\] is perpendicular to \[BC\].
Let \[E\left( {{x_2},{y_2}} \right)\] be a point on \[AC\] and \[BE\] is perpendicular to \[AC\].
Now we will find the slopes of \[BC\], \[AD\], \[BE\], and \[AC\].
The slope of the line \[BC\] is \[\dfrac{{ - 5 - 1}}{{5 + 7}} = \dfrac{{ - 6}}{{12}} = - \dfrac{1}{2}\].
The slope of the line \[AD\] is \[\dfrac{{{y_1} - 7}}{{{x_1} + 1}}\].
The slope of the line \[AC\] is \[\dfrac{{ - 5 - 7}}{{5 + 1}} = \dfrac{{ - 12}}{6} = - 2\].
The slope of the line \[AD\] is \[\dfrac{{{y_2} - 1}}{{{x_2} + 7}}\].
Since \[AD\] is perpendicular to \[BC\].
\[\dfrac{{{y_1} - 7}}{{{x_1} + 1}} \cdot \left( { - \dfrac{1}{2}} \right) = - 1\]
\[ \Rightarrow {y_1} - 7 = 2\left( {{x_1} + 1} \right)\]
Replace \[{x_1}\] by \[x\] and \[{y_1}\] by \[y\] to find the equation \[AD\]
\[ \Rightarrow y - 7 = 2\left( {x + 1} \right)\]
\[ \Rightarrow y - 7 = 2x + 2\]
\[ \Rightarrow 2x - y + 9 = 0\] ….(i)
Since \[BE\] is perpendicular to \[AC\].
\[\dfrac{{{y_2} - 1}}{{{x_2} + 7}} \cdot \left( { - 2} \right) = - 1\]
\[ \Rightarrow 2\left( {{y_2} - 1} \right) = \left( {{x_2} + 7} \right)\]
Replace \[{x_2}\] by \[x\] and \[{y_2}\] by \[y\] to find the equation \[AD\]
\[ \Rightarrow 2\left( {y - 1} \right) = x + 7\]
\[ \Rightarrow 2y - 2 = x + 7\]
\[ \Rightarrow x - 2y + 9 = 0\] ….(ii)
Now multiply 2 with equation (ii) and subtract (i) from it
\[2x - 4y + 18 = 0\]
\[2x - y + 9 = 0\]
\[\overline {\,\,\,\, - 3y + 9 = 0} \]
\[ \Rightarrow 3y = 9\]
\[ \Rightarrow y = 3\]
Substitute \[y = 3\] in equation (i)
\[2x - 3 + 9 = 0\]
\[ \Rightarrow 2x = - 6\]
\[ \Rightarrow x = - 3\]
The coordinate of the orthocentre is \[\left( { - 3,3} \right)\]
Hence option A is the correct option.
Note: An orthocentre is a point that is an intersection point of perpendicular lines which are drawn from a vertex to the opposite side.
Sometimes students take midpoint of \[BC\] to calculate perpendicular line on \[BC\] through the vertex \[A\]. This is an incorrect way. The perpendicular line may not pass through the midpoint. Thus we will assume the coordinate of point \[D\] and \[E\] on the lines \[BC\] and \[AC\] respectively.
Recently Updated Pages
Geometry of Complex Numbers Explained

JEE General Topics in Chemistry Important Concepts and Tips

JEE Extractive Metallurgy Important Concepts and Tips for Exam Preparation

JEE Amino Acids and Peptides Important Concepts and Tips for Exam Preparation

JEE Atomic Structure and Chemical Bonding important Concepts and Tips

Electricity and Magnetism Explained: Key Concepts & Applications

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

JEE Main Marking Scheme 2026- Paper-Wise Marks Distribution and Negative Marking Details

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

NCERT Solutions For Class 11 Maths Chapter 12 Limits and Derivatives (2025-26)

NCERT Solutions For Class 11 Maths Chapter 10 Conic Sections (2025-26)

Understanding the Electric Field of a Uniformly Charged Ring

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

Derivation of Equation of Trajectory Explained for Students




