




Introduction to Atomic Structure and Chemical Bonding
In this chapter, we'll look at the structure of atoms, as well as the subatomic particles that make up atoms. To comprehend bond formation, one must first understand the overall characteristics of atoms' electronic structure, or the arrangement of electrons around the central nucleus.
This chapter is one of the most significant for competitive tests like JEE, and mastering it will help you score well on the exams.
Important Topics of Atomic Structure and Chemical Bonding
Structure of Atom
Subatomic Particles
Electron
Discovery of Protons and Neutrons
Charge to Mass Ratio of an Electron
Electron and Electron Charge
Atomic Number and Mass Number, Isotopes and Isobars
Rutherford Atomic Theory
VSEPR Theory
Fajan’s rule
Bohr’s Atomic Model
Important Definitions of Atomic Structure and Chemical Bonding:
Subatomic Particles and Their Properties
An atom is made up of three subatomic or fundamental particles which are electrons, protons, and neutrons.
Table: Properties of subatomic particles
Rutherford's Nuclear Model of Atom
In Rutherford's $\alpha$-particle scattering experiment, a thin foil of gold is bombarded with $\alpha$ particles. The majority of the $\alpha$ particles passed undeflected and very few were deflected with small angles. The observations on the basis of deflection are as follows:
Mostly, the $\alpha$ particles passed through the gold foil, undeflected.
The small fraction of $\alpha$ particles were deflected by small angles.
Very few $\alpha$ particles deflected back (i.e. 180oC).
Conclusion of Rutherford's nuclear model of the atom
The positively charged and densely concentrated very small particle is present at the centre which is called the nucleus.
The electrons revolve around the nucleus at high speed in circular paths known as orbits.
Electrons and nucleus are held together by the electrostatic force of attraction.
Limitations of Rutherford's nuclear model of the atom
The stability of the atom could not be explained by Rutherford’s model.
It also could not tell about the electronic distribution around the nucleus and the energies of these electrons.
Wave Nature of Electromagnetic Radiation
Electromagnetic radiation is the continuous emission of energy from a source in the form of a wave of the electric and magnetic field, oscillating perpendicular to each other and perpendicular to the direction of propagation of the wave.
Electromagnetic radiations arranged in the increasing order of their wavelengths or decreasing order of frequencies are known as the electromagnetic spectrum. A small portion of the electromagnetic spectrum is visible to give a visible spectrum.
Electromagnetic radiations, in a vacuum, travel with the speed of light (c) i.e. 3 X 108 ms-1 and the frequency ($\nu$), wavelength ($\lambda$), and speed of light are related by the equation:
c = $\nu\lambda$
Particle Nature of Electromagnetic Radiation
Plank’s Quantum Theory: Quantum is the smallest discontinuous packet of energy emitted or absorbed by the electromagnetic radiation which is given as:
E = h $\nu$
where h : Planck’s constant has value 6.626 X 10-34 Js
$\nu$ : frequency
Total energy emitted or absorbed is given by E = nh$\nu$
Photoelectric Effect: When the radiation of a certain minimum frequency ($\nu$0) strikes the surface of a metal and ejects the electron. The minimum energy (h$\nu$0) is called the wave function. The ejected electron ejects with some kinetic energy having velocity v.
h$\nu$ = (h$\nu$0) + ½ mev2
where me: Mass of electron
h: Planck’s constant
$\nu$0 : Threshold frequency
Line Spectrum of Hydrogen
Johannes Rydberg gave the formula to find the wavenumber of all series of the line spectrum of hydrogen or hydrogen-like species.
⊽ = RH $\left(\dfrac{1}{n_{1}^{2}} - \dfrac{1}{n_{2}^{2}}\right)$
where ⊽ : Wave number
RH: Rydberg’s constant = 109677 cm-1
Table: n1, n2, and the spectral region corresponding to the series of transition
Bohr’s Model for Hydrogen Atom
Postulates of Bohr’s model of hydrogen atom
The electron in a hydrogen atom revolves around the nucleus in a fixed circular path with fixed energy and radius. These circular paths are known as orbits.
In a specific orbit, the energy of electrons remains constant.
The electron moves from a lower energy state to a higher energy state by absorbing energy whereas the electron moves from a higher energy state to a lower energy state by emission of energy.
The frequency of radiation emitted or absorbed is given by Bohr as:
v = $\dfrac{\Delta E}{h}$ = $\dfrac{ E_2 - E_1}{h}$
where E2 and E1 are the higher energy state and lower energy state, respectively, and the expression is known as Bohr's frequency rule.
Angular momentum of an electron in a particular stationary orbit is represented by the equation:
mevr = n $\dfrac {h}{2\pi}$
where n is an integer and known as the principal quantum number. The expression implies that the electron can move only in those orbits which have an integral multiple of angular momentum.
Bohr’s equations:
Energy of the stationary state:
En = - 2.18 X 10 -18 X Z2 X $\left(\dfrac{1}{n^{2}} \right)$ J
En = - 13.6 X Z2 X $\left(\dfrac{1}{n^{2}} \right)$ eV
Radius of orbit:
rn = ao $\left(\dfrac{n^{2}}{Z} \right)$ pm
ao: Bohr’s radius = 52.9 pm
Velocity of electron:
Vn = 2.165 X 106 X $\left(\dfrac{Z}{n} \right)$ ms-1
Dual Behaviour of Particle
According to de Broglie, every moving object has a wave character but the wavelength associated with some objects is so short that the wave character cannot be detected. The wavelength (λ) can be calculated by the expression given by de Broglie as:
λ = $\dfrac{h}{p}$ = $\dfrac{h}{mv}$
Where p: momentum
Heisenberg's Uncertainty Principle
According to Heisenberg's Uncertainty Principle, it is impossible to measure the exact position and momentum or velocity of a particle simultaneously. There is a mathematical expression to measure the uncertainty of position and uncertainty of velocity as:
Δx . Δp ≥ $\dfrac{h}{4\pi}$
Δx . Δv ≥ $\dfrac{h}{4m \pi}$
This shows that the product of the uncertainty in position (Δx) and uncertainty in momentum (Δp) is always greater than and equal to a constant which is h/4π.
Quantum Mechanical Model of Atom
It deals with the study of the motion or the position of microscopic objects which have both wave character and particle character. The basic equation of quantum mechanics was developed by Schrodinger and the equation is simply written as:
H Ψ = E Ψ
where H is an operator known as a Hamiltonian operator, Ψ is the wavefunction, and E is the energy eigenvalue for the system.
Quantum Numbers
Quantum numbers are the set of numbers which give the complete information about the position of electrons in the atom. There is a set of four quantum numbers, which are:
Principal Quantum Number(n) : It tells about the size of the orbital and the energy of the shell in which an electron is present. Principal quantum number (n) can have integral values such as 1, 2, 3……. and the maximum number of electrons present in the nth shell is 2n2.
Azimuthal Quantum Number(l): It determines the shape of the subshell and the number of subshells present in the shell. Azimuthal quantum number also known as the angular momentum and its value ranges from (l) = 0,1,2…… (n - 1) to denote the number of subshells present in the principal shell.
Table: Azimuthal quantum number: Number of subshells and the subshell corresponding to the particular value of I
Magnetic Quantum Number (ml): It determines the number of orbitals present in the subshells and gives information about the orientation of each orbital. The value of magnetic quantum number (ml) ranges from -l to +l for a given value of l, so the total number of allowed values of magnetic quantum number is 2l + 1. For, l = 2; ml values will be -2, -1, 0, 1, 2.
Table: The number of orbitals corresponding to the given value of l.
Spin Quantum Number (ms): It tells about the spinning motion of electrons which can be clockwise or anti-clockwise. The value for the clockwise motion of electrons is + ½ and for anti-clockwise motion, it is -½ and these are known as two spin states of electrons.
Shapes of Atomic Orbitals
The shape of the orbital can be determined by the probability (ψ2) of finding the electron in the region of the orbital. There are regions in the orbital where the probability of finding electrons is zero and these regions are known as the nodes. The total number of nodes for the nth shell is (n - 1) of which angular or planar nodes are l and radial or spherical nodes are n - l -1.
Rules for Filling of Electrons in Orbitals
The electron in the orbitals of different atoms is filled according to the following rules and principles:
Aufbau Principle: The energy of the orbital is given by the sum of n + l. This principle states that “In the ground state of the atom, the orbitals are filled in the increasing order of energy”. For the same value of n + l , the energy will be lower for which the value of n is lower.
The increasing order of energy and hence the order of filling of electron in the orbital is as follows:
1s < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d < 5p < 6s < 4f < 5d < 6p < 7s
(n + l) : 1 2 3 3 4 4 5 5 5 6 6 6 7 7 7 7
value
Hund's Rule of Maximum Multiplicity: It states that “pairing of electrons in the orbital of the same subshell does not take place until each orbital of that subshell is singly occupied. ”
Pauli Exclusion Principle: It states that “no two electrons in an atom can have the same set of all the four quantum numbers. ”
Electronic Configuration of Atom
It is the distribution of electrons in the orbitals of the shell according to the increasing order of energy level as shown below:
O : 1s2, 2s2, 2p4
where the electron in the outer same shells are known as valence electrons such as in oxygen the valence electron in the outer shell (n = 2) is 2+4 = 6
Octet Rule
According to octet rule, the atoms can combine by transfer of electrons or by sharing of electrons to complete their octet i.e. to have 8 electrons in their outermost shell or valence shell.
Covalent Bond
The bond is formed by sharing of electrons between two or more atoms to attain the outer shell noble gas configuration i.e. to complete octet of valence shell.
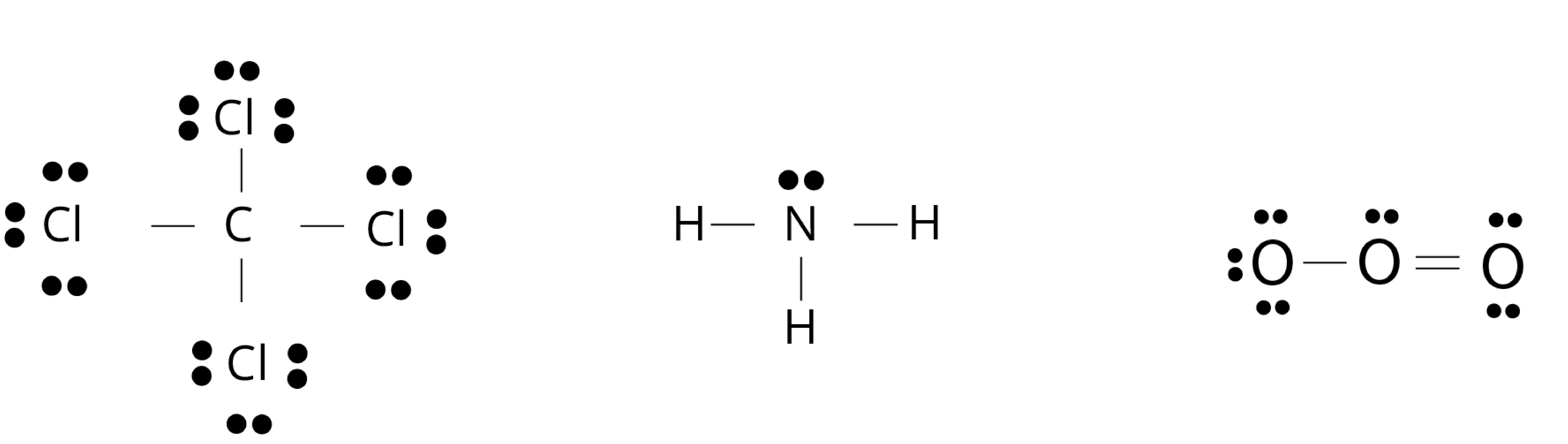
Lewis Dot Structure
The Lewis dot structure of a molecule shows bonding between the atoms of a molecule along with lone pair (s) of electrons. In the Lewis dot structure, the electrons are represented by dots around the atoms.
Conditions of the representation of lewis dot structure of molecule:
A bond is formed by the sharing of electron pair(s) between the two atoms of a molecule.
At least one electron is contributed to the shared electron pair by each combining atom.
The sharing of electrons is such that the combining atom attains the nearest noble gas configuration or complete octet of the valence shell.
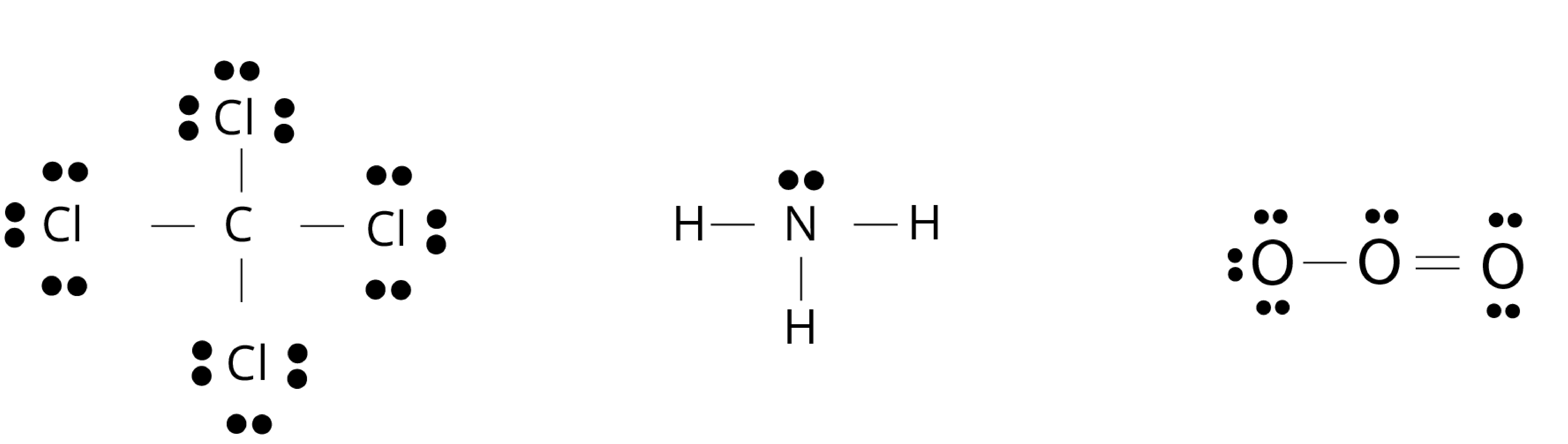
Fig: Lewis dot structure of carbon tetrachloride(CCl4), ammonia (NH3), and ozone (O3) molecule, the bond is formed by sharing of electrons from each atom for molecules.
Ionic or Electrovalent Bond
Ionic bond is formed by the transfer of electrons from one atom to another atom to form ionic bonds. The atoms lose or gain electrons to form positively charged ions (cations) or negatively charged ions (anions), respectively. There is a strong force of attraction between cations and anions due to the formation of ionic bonds.
Lattice Energy: Lattice energy of an ionic compound is the energy required to completely separate the one mole of the crystalline ionic compound into its gaseous constituents of ions.
Fajan’s Rule
It states that the covalent bond has some partial ionic character whereas the ionic bonds have partial covalent character. The partial covalent character in the ionic bond can be measured in terms of the following Fajan’s rule:
The smaller the size of the cation and the greater the size of the anion, the more will be the covalent character in the ionic bond.
The cations with greater charge contribute to the more covalent character in the ionic bond.
Transition metal cations are more polarising than the cation with noble gas configuration with the same charge and size as that of transition metal cation.
Valence Shell Electron Pair Repulsion (VSEPR) theory
This theory helps in determining the shape of the molecule of covalent compounds on the basis of the repulsion of the lone pair and bond pairs in the free spatial arrangement around the central atom of the molecule. The postulates of the VSEPR are as follows:
Only valence shell electron pairs around the central atom contribute to the shape of the molecule.
The electron pair repels each other as these are negatively charged due to their negatively charged electron cloud.
Electron pairs occupy the spherical space around the central atom such that they are at maximum distance from each other and have minimum repulsion between them.
Multiple bonds are treated as a single electron pair.
The repulsion order of bond pair(bp) and lone pair(lp) is:
lp-lp > lp-bp > bp-bp
Solved Examples from the Chapter
Example 1: The radius of the second Bohr orbit for the hydrogen atom is :
(a) 1.65 Å
(b) 4.76 Å
(c) 0.529 Å
(d) 2.12 Å
Solution: (a) We know the Bohr radius, rn is:
rn = 52.9 $\left(\dfrac{n^{2}}{Z} \right)$ pm = 0.529 $\left(\dfrac{n^{2}}{Z} \right)$ Å
Z = 1 for hydrogen atom and n= 2 for second Bohr orbit
∴ The radius of second Bohr orbit for hydrogen atom
r2 = 0.529 $\left(\dfrac{2^{2}}{1} \right)$ Å = 0.529 $\left(\dfrac{2^{2}}{1} \right)$ Å
= 0.529 X 4 ≈ 2.12 Å
Key points: Bohr’s radius, rn = 0.529 $\left(\dfrac{n^{2}}{Z} \right)$ Å
Example 2: Among the following, the maximum covalent character is shown by the compound :
(a) AlCl3
(b) MgCl2
(c) FeCl2
(d) SnCl2
Solution: (a) AlCl3 has the maximum covalent character in the given ionic compounds, due to maximum charge Al3+ while all other cations have +2 charge.
Key points: According to Fajan’s rule of covalent character in ionic bond, the cation with small size and greater charge has the maximum covalent character.
Solved Questions from the Previous Year Question Papers
Question 1: A certain orbital has no angular nodes and two radial nodes. The orbital is
2s
3s
3p
2p
Solution: (b) As the angular node is zero, l = 0, also radial nodes is two, n - l - 1 = 2
So, n - 0 - 1 = 2
n = 3
So, the orbital is 3 s [as n = 3 and l = 0].
Question 2: What is the work function of the metal if the light of wavelength 4000 Å generates photoelectrons of velocity 6 x 105 ms-1 from it ? (Mass of electron = 9 x 10-31 kg; Velocity of light = 3 x 108 ms-1; Planck's constant = 6.626 x 10-34 Js; Charge of electron = 1.6 x10-19 JeV-1)
4.0 eV
0.9 eV
2.1 eV
3.1 eV
Solution: (c) We know,
h$\nu$ = (h$\nu$0) + ½ mev2
Given, me = 9 x 10-31 kg
v = 6 x 105 ms-1
h = 6.626 x 10-34 Js
c = 3 x 108 ms-1
λ = 4000 Å
e = 1.6 x10-19 JeV-1
Work function (h$\nu$0) = ?
Now, we know that, ν = c / λ = 3 x 108 / 4000 X 10 -10 = ¾ X 1015
Now, putting the value of ν in above equation we get,
6.626 X 10-34 X ¾ X 1015 = (h$\nu$0) + ½ (9 x 10-31) ( 6 x 105 )2
h$\nu$0 = 3.35 X 10 -19 J
h$\nu$0 (in eV) = 3.35 X 10 -19 J / e = 3.35 X 10 -19 J / 1.6 x10-19 JeV-1 ≅ 2.1 eV
Question 3: The shape or structure of [XeF5]– and XeO3F2, respectively, are
Pentagonal planar and trigonal bipyramidal
Trigonal bipyramidal and pentagonal planar
Octahedral and square pyramidal
Trigonal bipyramidal and trigonal bipyramidal
Solution: (a) [XeF5]– : 5 bond pairs + 2 lone pairs ⟶ sp3d3 hybridisation ⇒ Pentagonal planar shape
XeO3F2: 5 bond pairs + 0 lone pairs ⟶ sp3d hybridisation ⇒ Trigonal bipyramidal shape
Practice Questions
Question 1: The isoelectronic set of ions is :
F-ー , Li+, Na+ and Mg2+
Li+, Na+, O2- and Fー
N3ー, O2ー, Fー and Na+
N3ー, Li+, Mg2+ and O2-
Answer: (c) N3ー, O2ー, Fー, and Na+
Question 2: The ground state energy of the hydrogen atom is -13.6 eV. The energy of the second excited state of He+ ion in eV is
-6.04
-54.4
-27.2
-3.4
Answer: (a) -6.04
Conclusion
It is concluded from various theories that the structure of atoms contains the negatively charged electron arranged in the orbital of the shell. These electrons revolve around the nucleus which contains neutrons and protons. The structure of atoms is the basis for the formation of bonds in the molecule. The valence shell electrons participate in the bond formation either by sharing electrons or transfer of electrons. The covalent bond which is formed by sharing electrons has some ionic character whereas the ionic bond which is formed by electron transfer has some covalent character which can be measured by Fajan’s rule.
Atomic structure and chemical bonding are collectively an important topic for the JEE competitive examination. One can find all types of questions easy, medium, and difficult from this chapter for the examination. This article covers all the major and important topics from the examination point of view.
FAQs on JEE Important Chapter - Atomic Structure and Chemical Bonding
1. Is atomic structure important for JEE?
Atomic structure is one of the important topics for competitive exams. This chapter is one of the easiest chapters as well as scoring. In the JEE examination, at least 2-3 questions of easy level in terms of difficulty level come in the examination.
2. What is the weightage of atomic structure in JEE Main?
In JEE main, the atomic structure is the one of the easiest chapters and at least 2-3 questions cover 8-12 marks and has 6-7% weightage in the JEE Main competitive examination paper.
3. Is the chemical bonding chapter important for JEE?
Yes, chemical bonding is an important chapter for JEE exam as the questions appearing in the examination paper are of easy level in terms of difficulty. The 2-3 questions from this chapter come in the exam papers.























