
Find the equation of the circle which touches both axes in the first quadrant and whose radius is a
A )$\quad x^{2}+y^{2}-2 a x-2 a y+a^{2}=0$
B )$\quad x^{2}+y^{2}-2 a x+2 a y-a^{2}=0$
C )$\quad x^{2}+y^{2}+2 a x-2 a y+a^{2}=0$
D ) None of the above
Answer
232.8k+ views
Hint:We have the general equation of circle. And it is given that the circle touches both axes in the first quadrant. So we can find the general equation of the given circle by substituting the a value. The radius of a circle is one of its most important features It is the separation between a point on a circle's edge and its center.
Complete step by step Solution:
Given,
In the first quadrant, a circle with radius a contacts both axes, hence its center will be $(a, a)$.
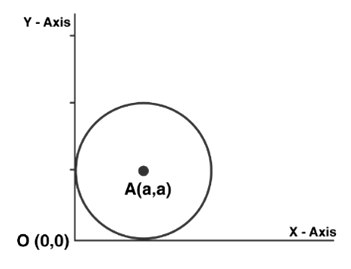
Therefore the required equation is
$\Rightarrow(x-a)^{2}+(y-a)^{2}=a^{2}$
$\Rightarrow x^{2}+a^{2}-2 a x+y^{2}+a^{2}-2 a y=a^{2}$
$\Rightarrow x^{2}+y^{2}-2 a x-2 a y+2 a^{2}-a^{2}=0$
$\Rightarrow {{x}^{2}}+{{y}^{2}}-2ax-2ay+{{a}^{2}}=0$
Therefore, the correct option is A.
Additional information:
The radius of a circle is the length of the straight line that connects the center to any point on its circumference. Because a circle's circumference can contain an endless number of points, a circle can have more than one radius. This indicates that a circle has an endless number of radii and that each radius is equally spaced from the circle's center. When the radius's length varies, the circle's size also changes.
Note: The equation for a circle has the generic form: ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$. The coordinates of the circle's center and radius are found using this general form, where g, f, and c are constants. The general form of the equation of a circle makes it difficult to identify any significant properties about any specific circle, in contrast to the standard form, which is simpler to comprehend. So, to quickly change from the generic form to the standard form, we will use the completing square formula.
Complete step by step Solution:
Given,
In the first quadrant, a circle with radius a contacts both axes, hence its center will be $(a, a)$.

Therefore the required equation is
$\Rightarrow(x-a)^{2}+(y-a)^{2}=a^{2}$
$\Rightarrow x^{2}+a^{2}-2 a x+y^{2}+a^{2}-2 a y=a^{2}$
$\Rightarrow x^{2}+y^{2}-2 a x-2 a y+2 a^{2}-a^{2}=0$
$\Rightarrow {{x}^{2}}+{{y}^{2}}-2ax-2ay+{{a}^{2}}=0$
Therefore, the correct option is A.
Additional information:
The radius of a circle is the length of the straight line that connects the center to any point on its circumference. Because a circle's circumference can contain an endless number of points, a circle can have more than one radius. This indicates that a circle has an endless number of radii and that each radius is equally spaced from the circle's center. When the radius's length varies, the circle's size also changes.
Note: The equation for a circle has the generic form: ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$. The coordinates of the circle's center and radius are found using this general form, where g, f, and c are constants. The general form of the equation of a circle makes it difficult to identify any significant properties about any specific circle, in contrast to the standard form, which is simpler to comprehend. So, to quickly change from the generic form to the standard form, we will use the completing square formula.
Recently Updated Pages
Geometry of Complex Numbers Explained

JEE General Topics in Chemistry Important Concepts and Tips

JEE Extractive Metallurgy Important Concepts and Tips for Exam Preparation

JEE Amino Acids and Peptides Important Concepts and Tips for Exam Preparation

JEE Atomic Structure and Chemical Bonding important Concepts and Tips

Electricity and Magnetism Explained: Key Concepts & Applications

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

JEE Main Marking Scheme 2026- Paper-Wise Marks Distribution and Negative Marking Details

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

NCERT Solutions For Class 11 Maths Chapter 12 Limits and Derivatives (2025-26)

NCERT Solutions For Class 11 Maths Chapter 10 Conic Sections (2025-26)

Understanding the Electric Field of a Uniformly Charged Ring

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

Derivation of Equation of Trajectory Explained for Students




