Question

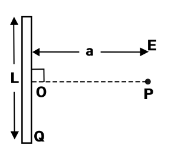
Find the electric field \[E\] at point \[P\] (as shown in the figure) on the perpendicular bisector of a uniformly charged thin wire of length \[L\] carrying a charge \[Q\]. The distance of the point \[P\] from the center of the rod is \[a = \left( {\frac{{\sqrt 3 }}{2}} \right)L\]

A. \[\frac{Q}{{2\sqrt 3 \pi {\varepsilon _o}{L^2}}}\]
B. \[\frac{{\sqrt 3 Q}}{{4\pi {\varepsilon _0}{L^2}}}\]
C. \[\frac{Q}{{3\pi {\varepsilon _o}{L^2}}}\]
D. \[\frac{Q}{{4\pi {\varepsilon _o}{L^2}}}\]

Answer 1

Hint: Write down the potential resulting from a point charge first. To determine the potential at point \[P\], integration on the line charge must be done. Therefore, choose a wire element \[\left( {dx} \right)\] and calculate its potential using the same methods as for a point charge.

Formula Used:
\[{{\rm{E}}_{{\rm{net }}}} = \frac{{{\rm{K}}\lambda }}{{\rm{r}}}\left( {\sin {\theta _1} + \sin {\theta _2}} \right)\]
Where \[{\theta _1},{\theta _2}\] are angle making with point \[{\rm{P}}\] from end.
Charge per unit length is \[\lambda \]

Complete answer:
We have been given in the question that,
Length of the wire \[ = L\]
Charge in the wire \[ = Q\]
Distance of the point \[P\] from the center of the rod is \[a = \left( {\frac{{\sqrt 3 }}{2}} \right)L\]

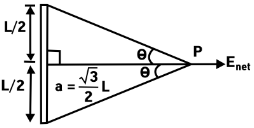
From the above diagram, we get
\[\tan \theta = \frac{{{\rm{ Perpendicular }}}}{{{\rm{ Base }}}}\]
Now, we have to observe the diagram and write the values in the above formula, we obtain\[\tan \theta = \frac{{\frac{L}{2}}}{{\frac{{\sqrt 3 }}{2}L}} = \frac{1}{{\sqrt 3 }}\]
On solving the above equation, we get
\[\theta = {30^\circ }\]
Now, we have to find electric field \[E\] at point \[P\]
Now,
\[{E_{net}} = \left( {\frac{{kQ}}{{\frac{{\sqrt 3 {L^2}}}{2}}}} \right)\left( {\sin {{30}^\circ } + \sin {{30}^\circ }} \right)\]
On solving the above equation by multiplying the terms inside the parentheses, we get
\[ = \left( {\frac{{2kQ}}{{\sqrt 3 {L^2}}}} \right)\left( {\frac{1}{2} + \frac{1}{2}} \right)\]
Now, we have to simplify the resultant equation, we have
\[ = \frac{1}{{4\pi {\varepsilon _0}}}\left( {\frac{{2Q}}{{\sqrt 3 {L^2}}}} \right)\]
On canceling the similar terms in the above expression, we get
\[ = \frac{Q}{{2\sqrt 3 \pi {\varepsilon _0}{L^2}}}\]
Where: The net electric field is \[{\rm{E}}\].
The constant is \[{\rm{K}}\].
The charge in the wire is \[{\rm{Q}}\].
The wire's length is \[{\rm{L}}\].
Absolute permittivity is \[{\varepsilon _0}\].
Therefore, the electric field \[E\] at point \[P\] (as shown in the figure) on the perpendicular bisector of a uniformly charged thin wire of length \[L\] carrying a charge \[Q\] is \[\frac{Q}{{2\sqrt 3 \pi {\varepsilon _0}{L^2}}}\].

Hence, the option A is correct.

Note: Students are likely to make mistake in these types of problems. In a brief, it can be claimed that because electric potential is a scalar number, it is zero at all points along the perpendicular bisector. The position of the force on a positive test charge is assumed to equal the position of the field.