Question

Equivalent capacitance between $A$ and $B$ in the figure is

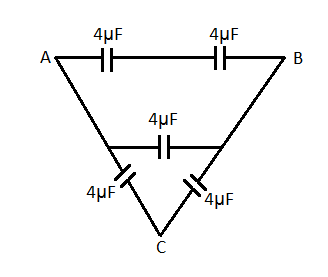
$A)\text{ }20\mu F$
$B)\text{ }8\mu F$
$C)\text{ }12\mu F$
$D)\text{ }16\mu F$

Answer 1

Hint: This problem can be solved by identifying which capacitors are in series and which sets are in parallel. By using the formulas for the equivalent capacitances for series and parallel combinations, we can get the equivalent capacitance between the required points.

Formula used:
${{C}_{equivalent,parallel}}=\sum\limits_{i=1}^{k}{{{C}_{i}}}$
$\dfrac{1}{{{C}_{equivalent,series}}}=\sum\limits_{i=1}^{k}{\dfrac{1}{{{C}_{i}}}}$

Complete step by step answer:
We will solve this problem by identifying which sets of capacitors are in parallel and which are in series and apply the respective formulas for the equivalent capacitances.
First let us draw a diagram wherein we name all the capacitors.

As we can see, ${{C}_{1}},{{C}_{2}}$ and ${{C}_{4}},{{C}_{5}}$ are in series respectively, whereas $\left( {{C}_{1}},{{C}_{2}} \right),{{C}_{3}},\left( {{C}_{4}},{{C}_{5}} \right)$ are three parallel branches.
Hence, let the equivalent capacitance of the series combination of ${{C}_{1}},{{C}_{2}}$ be ${{C}_{series-1}}$.
Similarly, let the equivalent capacitance of the series combination of ${{C}_{4}},{{C}_{5}}$ be ${{C}_{series-2}}$.
The equivalent capacitance between $A$ and $B$ will be ${{C}_{series-1}}||{{C}_{3}}||{{C}_{series-2}}$, that is the equivalent capacitance of the parallel combination of ${{C}_{series-1}}$,${{C}_{3}}$ and ${{C}_{series-2}}$.
Let this required capacitance be $C$.
Now, as given in the question the capacitance value of
${{C}_{1}}={{C}_{2}}={{C}_{3}}={{C}_{4}}={{C}_{5}}=4\mu F$.
Hence, let us find ${{C}_{series-1}}$ and ${{C}_{series-2}}$.
The equivalent capacitance ${{C}_{equivalent,series}}$ of $k$ capacitors of individual capacitances ${{C}_{i}}\left( i=\left[ 1,k \right] \right)$ is given by
$\dfrac{1}{{{C}_{equivalent,series}}}=\sum\limits_{i=1}^{k}{\dfrac{1}{{{C}_{i}}}}$ --(1)
Hence, using (1), we get,
$\dfrac{1}{{{C}_{series-1}}}=\dfrac{1}{{{C}_{1}}}+\dfrac{1}{{{C}_{2}}}=\dfrac{1}{4}+\dfrac{1}{4}=\dfrac{1}{2}\mu F$
$\therefore {{C}_{series-1}}=2\mu F$ --(2)
Similarly, using (1), we get,
$\dfrac{1}{{{C}_{series-2}}}=\dfrac{1}{{{C}_{4}}}+\dfrac{1}{{{C}_{5}}}=\dfrac{1}{4}+\dfrac{1}{4}=\dfrac{1}{2}\mu F$
$\therefore {{C}_{series-2}}=2\mu F$ --(3)
Now, the equivalent capacitance ${{C}_{equiva\operatorname{l}ent,parallel}}$ of $k$ capacitors of individual capacitances ${{C}_{i}}\left( i=\left[ 1,k \right] \right)$ is given by
${{C}_{equivalent,parallel}}=\sum\limits_{i=1}^{k}{{{C}_{i}}}$ --(4)
Now, since the required equivalent capacitance is the parallel combination of ${{C}_{series-1}}$,${{C}_{3}}$ and ${{C}_{series-2}}$ as explained above,
using (4), we get
$C={{C}_{series-1}}+{{C}_{3}}+{{C}_{series-2}}$
Using (2) and (3), we get,
$C=2+4+2=8\mu F$
Hence, the required equivalent capacitance between $A$ and $B$ is $8\mu F$.
Hence, the correct option is $B)\text{ }8\mu F$.

Note: Students must carefully see and determine across which two points the equivalent capacitance of the circuit is being asked. This is because in general, the equivalent capacitance of the circuit is different for different sets of terminals or points. Questions are sometimes purposely set in such a way so that the figure looks as if one has to find out the equivalent capacitance across one set of terminals but actually the question requires the equivalent capacitance across a completely different set. This is done predominantly to confuse students and tempt them into making a silly mistake.