Chemical Kinetics Class 12 Notes NEET Chemistry (Free PDF Download)

Kinetics 

(Kinesis: Movement) 

Kinetics is the branch of chemistry that studies the rates of chemical reactions, the factors that influence the rates of the reactions, and the mechanism by which the reactions occur.

Classification of Reactions: 

In terms of rates:

• Rapid reactions, such as the precipitation of AgCl

• Very slow reactions, such as iron rusting

• Reactions occur at a moderate rate. For example, hydrolysis of starch.

Rate of a Chemical Reaction 

A reaction's rate is defined as the change in concentration of a reactant or product per unit of time.

Average Rate 

The average rate of a reaction is the rate of reaction measured over a specific time interval. Consider the following hypothetical reaction:

${\rm{R}} \to {\rm{P}}$  

$\begin{array}{*{20}{l}}{{\rm{Average rate of reaction  =  }}\dfrac{{\left( {{\rm{Decrease in concentration of R}}} \right){\rm{ }}}}{{\left( {{\rm{Time taken}}} \right)}}}\\{{\rm{ =  }}\dfrac{{\left[ {\Delta {\rm{R}}} \right]}}{{\Delta{\rm{t}}}}}\\{\rm{\;}}\\\begin{array}{l}{\rm{Or}}\\{\rm{Average rate of reaction  =  }}\dfrac{{\left( {{\rm{Increase in concentration of P}}} \right){\rm{ }}}}{{\left( {{\rm{Time taken}}} \right)}}\\{\rm{ =  }}\dfrac{{\left[ {\Delta {\rm{P}}} \right]}}{{\Delta {\rm{t}}}}\end{array}\end{array}$ 

Instantaneous Rate 

The rate of change in concentration of any of the reactants or products at that specific instant of time is referred to as instantaneous rate.

As 

$\begin{array}{l}{\rm{\Delta t}} \to {\rm{0 }}\\{\rm{or }}\\{{\rm{r}}_{{\rm{inst}}}}{\rm{ =  }}\dfrac{{{\rm{ - d}}\left[ {\rm{R}} \right]}}{{{\rm{dt}}}}{\rm{ =  }}\dfrac{{{\rm{d}}\left[ {\rm{P}} \right]{\rm{\;}}}}{{{\rm{dt}}}}\end{array}$ 

Important: 

The reaction rate is always positive. Because [R] is a negative quantity (as the concentration of reactants decreases), it is multiplied by –1 to make the rate of the reaction positive.

Units of Rate of a Reaction: 

The units of rate are concentration time^–1 .

e.g. ${\rm{mol }}{{\rm{L}}^{{\rm{-1}}}}{\rm{s}}{{\rm{ }}^{{\rm{-1}}}}{\rm{; atm }}{{\rm{s}}^{{\rm{-1}}}}$  (for gaseous reactions) 

Overall Rate of a Reaction 

When there are multiple reactants and products, the individual rates of the various components may differ due to stoichiometric coefficients.

For a reaction, 

${\rm{A  +  2B }} \to {\rm{3C  +  4D}}$  

Rate of disappearance of B = 2 × Rate of disappearance of A (2:1) 

Rate of formation of C = 3 × Rate of disappearance of A 

(3:1) 

Rate of formation of D = 4 × Rate of disappearance of A 

(4:1) 

We divide the individual rates by the respective coefficients and equate their signs to define a unique value for the overall rate of the reaction.

$\begin{array}{l}{\rm{Overall Rate  =  - A / t  =  }}\left( {{\rm{-1/2}}} \right){\rm{ B/ t  =  }}\left( {{\rm{ + 1/3}}} \right){\rm{ C/ t }}\\{\rm{ =  }}\left( {{\rm{ + 1/4}}} \right){\rm{ D / t}}\end{array}$ 

Dependence of Rate on Concentration 

Concentration of reactants (pressure in the case of gases), temperature, and catalyst are all factors that influence the rate of a reaction.

Dependence on Concentration: 

Rate law 

Consider a general reaction 

${\rm{aA  +  bB }} \to {\rm{cC  +  dD}}$ 

The rate expression for this reaction is 

${\rm{Rate }} \propto {\rm{ }}{\left[ {\rm{A}} \right]^x}{\rm{ }}{\left[ {\rm{B}} \right]^y}$ 

where exponents x and y may or may not be equal to the stoichiometric coefficients (a and b) of the reactants. 

$\begin{array}{l}{\rm{Rate  = }}k{\left[ {\rm{A}} \right]^x}{\rm{ }}{\left[ {\rm{B}} \right]^y}\\ - d\left[ R \right]/dt = k{\left[ {\rm{A}} \right]^x}{\rm{ }}{\left[ {\rm{B}} \right]^y}\end{array}$
Above equation is known as differential rate equation, k is a proportionality constant called rate constant. 

In a balanced chemical equation, the rate law is the expression in which the reaction rate is given in terms of molar concentration of reactants, with each term raised to some power, which may or may not be the same as the stoichiometric coefficient of the reacting species.

Important 

The rate law for any reaction cannot be predicted theoretically by simply looking at the balanced chemical equation, but must be determined experimentally.

$\begin{array}{l}{\rm{2NO}}\left( {\rm{g}} \right){\rm{  +  }}{{\rm{O}}_{\rm{2}}}{\rm{ }}\left( {\rm{g}} \right) \to {\rm{\;2N}}{{\rm{O}}_{\rm{2}}}{\rm{ }}\left( {\rm{g}} \right){\rm{ Rate  =  k }}{\left[ {{\rm{NO}}} \right]^{\rm{2}}}\left[ {{{\rm{O}}_{\rm{2}}}} \right]{\rm{ }}\\{\rm{CHC}}{{\rm{l}}_{\rm{3}}}{\rm{  +  C}}{{\rm{l}}_{\rm{2}}} \to {\rm{CC}}{{\rm{l}}_{\rm{4}}}{\rm{  +  HCl        Rate  =  k }}\left[ {{\rm{CHC}}{{\rm{l}}_{\rm{3}}}} \right]{\left[ {{\rm{C}}{{\rm{l}}_{\rm{2}}}} \right]^{\dfrac{1}{2}}}\end{array}$ 

Order of a Reaction 

${\rm{aA  +  bB }} \to {\rm{cC  +  dD}}$  

${\rm{Rate}} = k{\left[ {\rm{A}} \right]^x}{\left[ {\rm{B}} \right]^y}$ 

The sum of these exponents, x + y, represents the overall order of a reaction, where x and y represent the order with respect to reactants A and B, respectively. As a result, the order of that chemical reaction is defined as the sum of powers of the concentration of the reactants in the rate law expression.

Order of a reaction can be 0, 1, 2, 3 and even a fraction. 

Units of Rate Constant 

${\rm{Rate}} = k{\left[ {\rm{A}} \right]^x}{\left[ {\rm{B}} \right]^y}$ 

$k = \dfrac{{{\rm{Rate}}}}{{{{\left[ {\rm{A}} \right]}^x}{{\left[ {\rm{B}} \right]}^y}}} = \dfrac{{{\rm{concentration}}}}{{{\rm{time}}}} \times \dfrac{1}{{{{\left( {{\rm{concentration}}} \right)}^n}}}$ 

Integrated Rate Equations 

Zero Order Reaction:

The rate of the reaction is proportional to the zero power of the reactant concentration.$\begin{array}{l}{\rm{R}} \to {\rm{P}}\\{\rm{Rate  =   - }}\dfrac{{\left[ {d{\rm{R}}} \right]}}{{dt}} = k{\rm{R}}^\circ \end{array}$

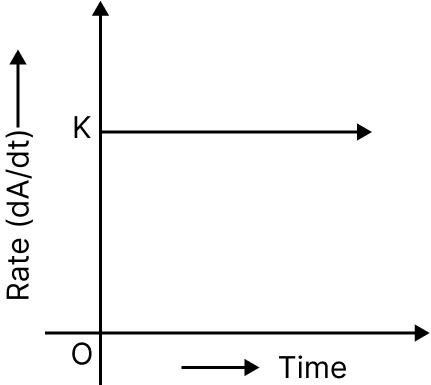
Zero Order Reaction

Consider the reaction, 

$\begin{array}{l}{\rm{R}} \to {\rm{P}}\\{\rm{Rate}} =  - \dfrac{{d\left[ {\rm{R}} \right]}}{{dt}}{\rm{  =  }}k{\left[ {\rm{R}} \right]^{\rm{^\circ }}}\;\\{\rm{Rate}} =  - \dfrac{{d\left[ {\rm{R}} \right]}}{{dt}}{\rm{  =  }}k \times 1\\\;d\left[ {\rm{R}} \right]{\rm{ }} = -{\rm{ }}kdt\end{array}$ 

Integrating both sides 

$\left[ {\rm{R}} \right] = -{\rm{ }}kt + {\rm{I}}$ 

where, I is the constant of integration. 

At t = 0, the concentration of the reactant R = [R]0, where [R]0 is initial concentration of the reactant. 

Substituting in equation 

$\begin{array}{*{20}{l}}{{{\left[ {\rm{R}} \right]}_{\rm{0}}}{\rm{  =  - k  \times  0  +  I}}}\\{{{\left[ {\rm{R}} \right]}_{\rm{0}}}{\rm{  =  I}}}\end{array}$ 

Substituting the value of I in the equation 

$\left[ {\rm{R}} \right]{\rm{  =  -kt  +  }}{\left[ {\rm{R}} \right]_{\rm{0}}}$ 

${\rm{k}} = \dfrac{{\left( {{{\left[ {\rm{R}} \right]}_0}} \right) - \left( {\left[ {\rm{R}} \right]} \right)}}{t}$ 

First Order:

The rate of the reaction is directly related to the first power of the concentration of the reactant R.

$\begin{array}{c}{\rm{R}} \to {\rm{P}}\\{\rm{Rate  =  }}\dfrac{{{\rm{ - d}}\left[ {\rm{R}} \right]}}{{{\rm{dt}}}} = k\left[ {\rm{R}} \right]\\\dfrac{{{\rm{ - d}}\left[ {\rm{R}} \right]}}{{\left[ {\rm{R}} \right]}} = k{\rm{dt}}\end{array}$ 

Integrating this equation, we get 

${\rm{ln }}\left[ {\rm{R}} \right]{\rm{  =  -kt  +  I }}........{\rm{ }}\left( {\rm{1}} \right)$ 

Again, I is the constant of integration and its value can be determined easily.

When ${\rm{t  =  0, R  =  }}{\left[ {\rm{R}} \right]_{\rm{0}}}{\rm{,}}$ where ${\left[ {\rm{R}} \right]_{\rm{0}}}$  is the initial concentration of the reactant. 

Therefore, equation can be written as 

$\begin{array}{*{20}{l}}{{\rm{ln }}{{\left[ {\rm{R}} \right]}_{\rm{0}}}{\rm{  =  - k  \times  0  +  I}}}\\{{\rm{ln }}{{\left[ {\rm{R}} \right]}_{\rm{0}}}{\rm{  =  I}}}\end{array}$ 

Substituting the value of I in equation 

${\rm{ln }}\left[ {\rm{R}} \right]{\rm{  =  -kt  +  ln }}{\left[ {\rm{R}} \right]_{\rm{0}}}{\rm{ }}.........{\rm{ }}\left( {\rm{2}} \right)$ 

Rearranging this equation 

$\begin{array}{l}\ln \dfrac{{\left[ {\rm{R}} \right]}}{{{{\left[ {\rm{R}} \right]}_0}}} =  - kt\\{\rm{or}}\\k = \dfrac{1}{t}\ln \dfrac{{{{\left[ {\rm{R}} \right]}_0}}}{{\left[ {\rm{R}} \right]}} \cdots  \cdots \left( 3 \right)\end{array}$ 

At time t1 from equation (2) 

${\rm{ln }}{\left[ {\rm{R}} \right]_1}{\rm{  =  -k}}{{\rm{t}}_1}{\rm{  +  ln }}{\left[ {\rm{R}} \right]_{\rm{0}}}$ 

At time t2 

${\rm{ln }}{\left[ {\rm{R}} \right]_2}{\rm{  =  -k}}{{\rm{t}}_2}{\rm{  +  ln }}{\left[ {\rm{R}} \right]_{\rm{0}}}$ 

where, ${\left[ {\rm{R}} \right]_{\rm{1}}}{\rm{and }}{\left[ {\rm{R}} \right]_{\rm{2}}}$ are the concentrations of the reactants at time ${{\rm{t}}_{\rm{1}}}{\rm{ and }}{{\rm{t}}_{\rm{2}}}$  respectively. 

Subtracting 

$\begin{array}{l}{\rm{ln }}{\left[ {\rm{R}} \right]_{\rm{1}}}{\rm{- ln}}{\left[ {\rm{R}} \right]_{\rm{2}}}{\rm{  =  - k}}{{\rm{t}}_{\rm{1}}}{\rm{ - }}\left( {{\rm{-k}}{{\rm{t}}_{\rm{2}}}} \right)\\{\rm{ln }}\dfrac{{{{\left[ {\rm{R}} \right]}_{\rm{1}}}}}{{{{\left[ {\rm{R}} \right]}_{\rm{2}}}}} = {\rm{k}}\left( {{{\rm{t}}_{\rm{2}}}{\rm{ - }}{{\rm{t}}_{\rm{1}}}} \right)\end{array}$ 

${\rm{k}} = \dfrac{1}{{\left( {{{\rm{t}}_{\rm{2}}}{\rm{ - }}{{\rm{t}}_{\rm{1}}}} \right)}}{\rm{ln }}\dfrac{{{{\left[ {\rm{R}} \right]}_{\rm{1}}}}}{{{{\left[ {\rm{R}} \right]}_{\rm{2}}}}}$ 

Comparing equation (2) with y = mx + c, if we plot In [R] against t, we get a straight line with slope = –k and intercept equal to ln [R]0

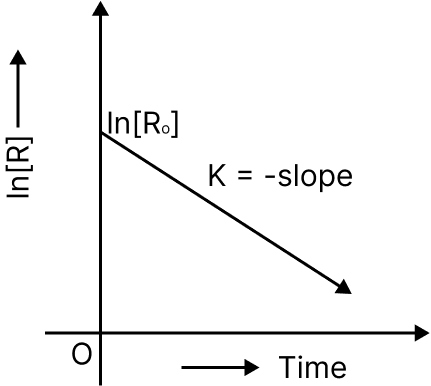
First Order

The first order rate equation (3) can also be written in the form

$\begin{array}{l}k = \dfrac{{2.303}}{t}\log \dfrac{{{{\left[ {\rm{R}} \right]}_0}}}{{\left[ {\rm{R}} \right]}}\\\log \dfrac{{{{\left[ {\rm{R}} \right]}_0}}}{{\left[ {\rm{R}} \right]}} = \dfrac{{kt}}{{2.303}}\end{array}$ 

Half-Life of a Reaction 

A reaction's half-life is the time it takes for the concentration of a reactant to be reduced to one-half of its initial concentration.

It is represented as ${t_{\dfrac{1}{2}}}$

 For a zero order reaction, rate constant is given by equation.

$k = \dfrac{{{{\left[ {\text{R}} \right]}_0} - \left[ {\text{R}} \right]}}{t}$

At $t = {t_{\dfrac{1}{2}}},{\text{ }}\left[ {\text{R}} \right] = \dfrac{1}{2}{\left[ {\text{R}} \right]_0}$

The rate constant at ${t_{\dfrac{1}{2}}}$ becomes

$k = \dfrac{{{{\left[ {\text{R}} \right]}_0} - \dfrac{1}{2}{{\left[ {\text{R}} \right]}_0}}}{{{t_{\dfrac{1}{2}}}}}$

${t_{\dfrac{1}{2}}} = \dfrac{{{{\left[ {\text{R}} \right]}_0}}}{{2k}}$

 For the first order reaction,

$k = \dfrac{{2.303}}{t}\log \dfrac{{{{\left[ {\rm{R}} \right]}_0}}}{{\left[ {\rm{R}} \right]}}$ 

At half time, $\left[ {\rm{R}} \right] = \dfrac{{{{\left[ {\rm{R}} \right]}_0}}}{2}$ 

So, the above equation becomes

$k = \dfrac{{2.303}}{{{t_{\dfrac{1}{2}}}}}\log \dfrac{{{{\left[ {\text{R}} \right]}_0}}}{{\dfrac{{\left[ {\text{R}} \right]}}{2}}}$

Or

${t_{\dfrac{1}{2}}} = \dfrac{{2.303}}{k}\log 2$

${t_{\dfrac{1}{2}}} = \dfrac{{2.303}}{k} \times 0.301$

${t_{\dfrac{1}{2}}} = \dfrac{{0.693}}{k}$

Pseudo First Order Reactions 

• Reactions that are not truly of the first order but become so under certain conditions. e.g.

• During the reaction, the concentration of water does not change significantly.

• So, in the rate equation the term $\left[ {{{\rm{H}}_{\rm{2}}}{\rm{O}}} \right]$  can be taken as constant.

Molecularity and Mechanism 

Molecularity: 

The number of reacting species (atoms, ions, or molecules) in an elementary reaction that must collide simultaneously in order to produce a chemical reaction is referred to as the molecularity of a reaction. Reaction classification based on molecularity:

• Unimolecular reactions: when only one reacting species is involved, such as ammonium nitrite decomposition

${\rm{N}}{{\rm{H}}_{\rm{4}}}{\rm{N}}{{\rm{O}}_{\rm{2}}} \to {\rm{\;}}{{\rm{N}}_{\rm{2}}}{\rm{  +  2}}{{\rm{H}}_{\rm{2}}}{\rm{O}}$ 

• Bimolecular reactions: It entails the simultaneous collision of two species, such as the dissociation of hydrogen iodide.

${\rm{2HI\;}} \to {{\rm{H}}_{\rm{2}}}{\rm{  +  }}{{\rm{I}}_{\rm{2}}}$ 

• Trimolecular or termolecular reactions: It entails the simultaneous collision of three reacting species, for example, 

${\rm{2NO  +  }}{{\rm{O}}_{\rm{2}}} \to {\rm{\;2N}}{{\rm{O}}_{\rm{2}}}$ 

• Reactions with molecularity greater than three are very rare. 

Mechanism 

The reactions that occur in a single step are referred to as elementary reactions. When a series of elementary reactions (referred to as a mechanism) produces the products, the reactions are referred to as complex reactions. The mechanism of the reaction refers to the various steps that occur during the complex reaction.

Rate Determining Step: 

The slowest step in a reaction, known as the rate determining step, controls the overall rate of the reaction. A complex reaction can be depicted as a series of simple steps.

As an example,

${\rm{2N}}{{\rm{O}}_{\rm{2}}}\left( {\rm{g}} \right){\rm{ +  }}{{\rm{F}}_{\rm{2}}}\left( {\rm{g}} \right){\rm{\;}} \to {\rm{2N}}{{\rm{O}}_{\rm{2}}}{\rm{F}}\left( {\rm{g}} \right)$ 

Experimentally, Rate of reaction ${\rm{ =  k}}\left[ {{\rm{N}}{{\rm{O}}_{\rm{2}}}} \right]\left[ {{{\rm{F}}_{\rm{2}}}} \right]$  

Probable mechanism: 

Step-1: 

${\rm{N}}{{\rm{O}}_{\rm{2}}}{\rm{  +  N}}{{\rm{O}}_{\rm{2}}} \to {\rm{\;NO  +  N}}{{\rm{O}}_{\rm{3}}}{\rm{ }}\left( {{\rm{slow}}} \right)$ 

Step-2: 

${\rm{N}}{{\rm{O}}_{\rm{3}}}{\rm{  +  CO}} \to {\rm{\;N}}{{\rm{O}}_{\rm{2}}}{\rm{  +  C}}{{\rm{O}}_{\rm{2}}}\left( {{\rm{fast}}} \right)$ 

Slow step: bimolecular 

Hence, a bimolecular reaction.

Reaction Intermediates: 

Some species are formed during the course of the reaction but do not appear in the final product. They are referred to as reaction intermediates.

e.g. NO3 in the above example. 

Difference Between Order and Molecularity of a Reaction:

Order 

1. In the rate law expression, order is the sum of the powers of the concentration of the reactants.

2. It can be zero or a fraction.

3. It is applicable to both simple and complex reactions.

4. It can only be determined experimentally and not calculated.

5. In a complex reaction, the order is determined by the slowest step.

Molecularity 

1. Molecularity is the number of reacting species in an elementary reaction that must collide at the same time in order for a chemical reaction to occur.

2. It can't be zero or anything else that isn't an integer.

3. It is only applicable to simple reactions. Molecularity has no meaning in a complex reaction.

4. It is simple to calculate by adding the molecules of the slowest step.

5. In general, the molecularity of the slowest step is the same as the overall reaction order.

Temperature Dependence 

Activation Energy 

• According to collision theory, a reaction occurs when reactant molecules collide with one another. 

• The minimum energy that colliding molecules must have in order for the collision to be effective is referred to as the threshold energy. 

• The activation energy is the smallest amount of extra energy absorbed by reactant molecules in order for their energy to equal the threshold value.

• Threshold energy = activation energy + the energy of the reactants

• The faster the reaction, the lower the activation energy. 

• In order for the reactants to become products, they must first cross an energy barrier (corresponding to threshold energy). 

• Reactant molecules absorb energy and form an intermediate known as an activated complex, which dissociates immediately to form the products.
  
  

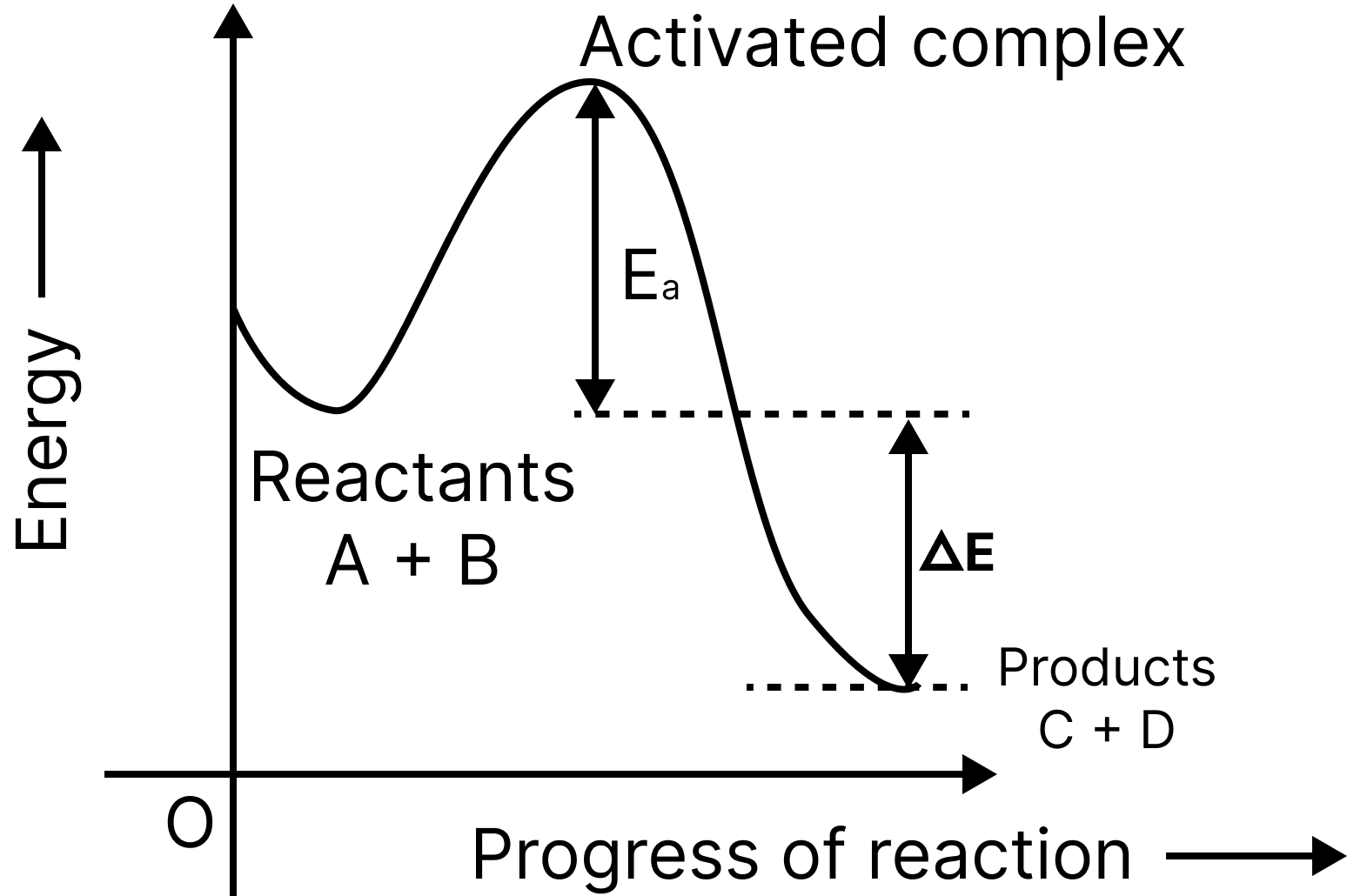
Exo-Reaction Pathway

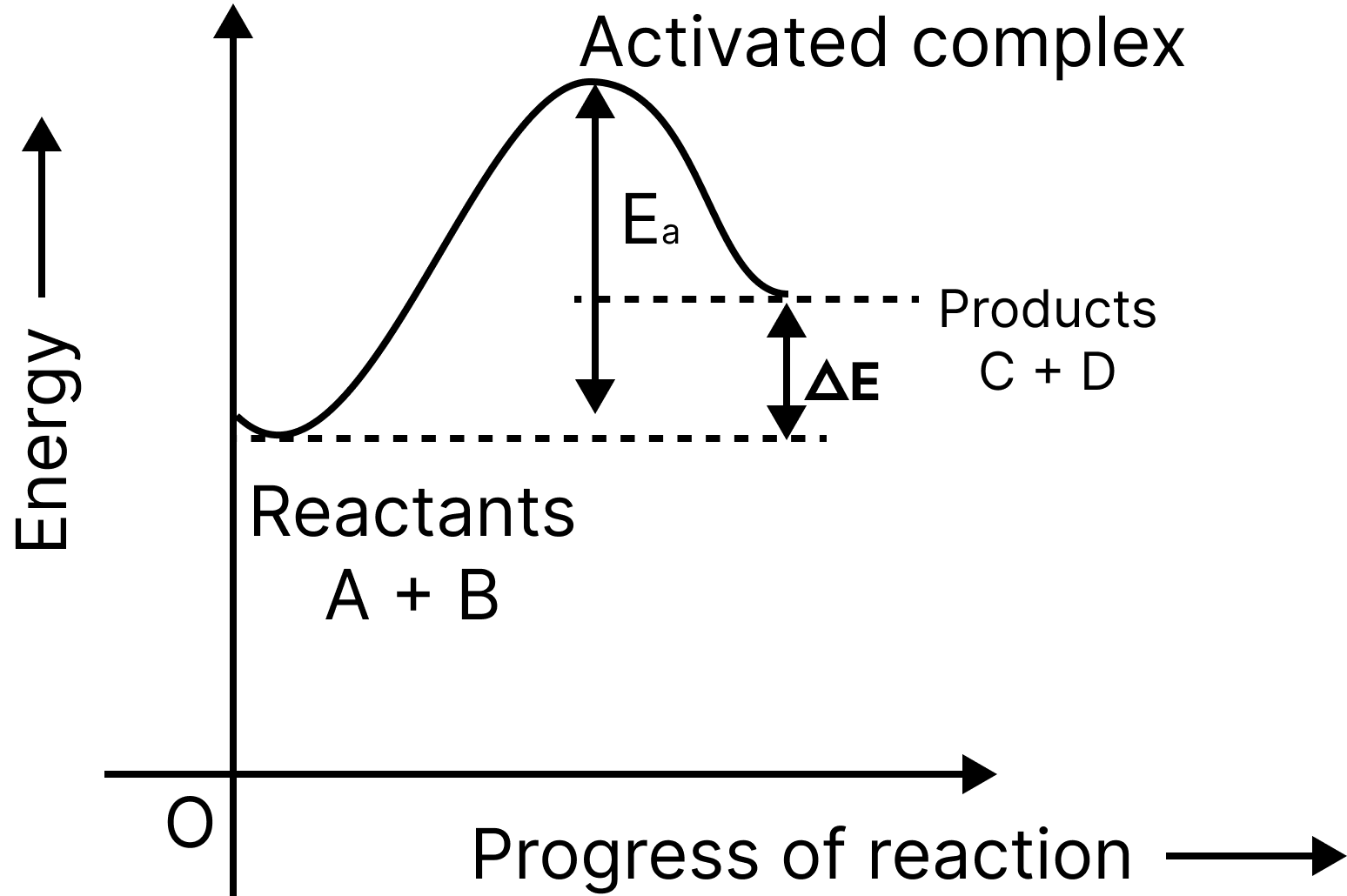
Endo-Reaction Pathway

Temperature Dependence of the Rate of a Reaction 

The rate constant of a chemical reaction nearly doubles when the temperature rises by 10⁰. 

Temperature coefficient = (Rate constant at T + 10⁰) / (Rate constant at T⁰) 

Arrhenius Equation 

The Arrhenius equation can quantitatively explain the temperature dependence of the rate of a chemical reaction.

$k = A{e^{ - {E_a}/RT}}$ 

Here, A is the Arrhenius factor or the frequency factor or the pre-exponential factor. R is gas constant and E_a is activation energy measured in joules/mole. 

The factor ${e^{ - {E_a}/RT}}$  represents the proportion of molecules with kinetic energy greater than Ea. As a result of the Arrhenius equation, it has been discovered that increasing the temperature or decreasing the activation energy results in an increase in the rate of the reaction and an exponential increase in the rate constant.

Effect of Catalyst 

A catalyst is a substance that changes the rate of a reaction without undergoing permanent chemical change.

Action of the Catalyst 

According to the intermediate complex theory, reactants first combine with the catalyst to form the intermediate complex, which then decomposes to form the products while also regenerating the catalyst.

Effect of Catalyst On Activation Energy

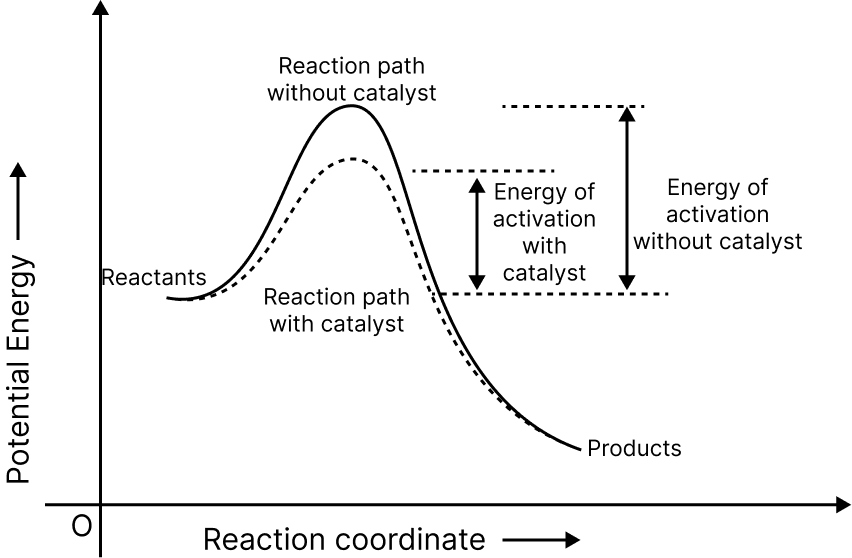
Effect of Catalyst

By lowering the activation energy between reactants and products and thus lowering the potential energy barrier, catalysts provide an alternate pathway.

Important Characteristics of Catalyst:

• It includes the ability of a small amount of catalyst to catalyze a large amount of reactants.

• A catalyst has no effect on the Gibbs energy, G, of a reaction.

• It catalyzes spontaneous reactions, but not non-spontaneous reactions.

• A catalyst does not change the equilibrium constant of a reaction; rather, it speeds up the process of reaching equilibrium.

Collision Theory of Chemical Reactions:

According to this theory, the reactant molecules are assumed to be hard spheres, and the reaction is thought to occur when the molecules collide. The rate of reaction is determined by the number of effective collisions, which is determined by:

(i) Energy factor: colliding molecules must have more energy than the threshold energy.

(ii) Steric or probability factor (P): colliding molecules must be oriented correctly at the time of the collision.

Examples:

1. In the presence of a catalyst, the heat evolved or absorbed during the reaction _____.

(A) increases

(B) decreases

(C) remains unchanged

(D) may increase or decrease

Correct Answer: Option (C)

Explanation:

A catalyst is a substance that enables a chemical reaction to proceed at a usually faster rate or under different conditions. So, a catalyst alters the enthalpy change i.e., heat of the reaction. So, in the presence of the reaction the enthalpy is not changed, which is it remains constant and there is no heat evolved or absorbed. Therefore, the correct option is C.

2. Activation energy of a chemical reaction can be determined by ________.

(A) determining the rate constant at standard temperature

(B) determining the rate constants at two temperatures

(C) determining probability of collision

(D) using catalyst

Correct Answer: (B)

Explanation:

Activation on energy of a chemical reaction can determined with the help of Arrhenius equation. This determines the rate constants at two temperatures.

$2.303\log \dfrac{{{K_2}}}{{{K_1}}} = \dfrac{{{E_a}}}{R}\left[ {\dfrac{{{T_2} - {T_1}}}{{{T_1}{T_2}}}} \right]$ 

Therefore, the correct option is B.

3. Consider a first order gas-phase decomposition reaction given below:

The initial pressure of the system before decomposition of A was${p_t}$  . After lapse of time ‘$t$ ’, total pressure of the system increased by $x$  units and became ‘$t$ ’ the rate constant $k$  for the reaction is given as _________.

(A) $k = \dfrac{{2.303}}{t}\log \dfrac{{{p_t}}}{{{p_t} - x}}$ 

(B) $k = \dfrac{{2.303}}{t}\log \dfrac{{{p_t}}}{{2{p_t} - {p_t}}}$ 

(C) $k = \dfrac{{2.303}}{t}\log \dfrac{{{p_t}}}{{2{p_t} + {p_t}}}$ 

(D) $k = \dfrac{{2.303}}{t}\log \dfrac{{{p_t}}}{{2{p_t} + x}}$ 

Correct answer: Option (B)

Explanation

Given: 

${p_i} =$Initial pressure

(Time) $t = 0$ 

 ${p_i} \to {0_{atm}} + {0_{atm}}$ 

$t,({p_i} - x)atm$ 

${p_t}_{} = ({p_{i}} - x)atm + x + x = {p_{i}} + x$ 

${p_A} = ({p_i} - x)$ 

On substitution the value of x becomes

${p_A} = {p_i} - ({p_t} - {p_i}) = 2{p_i} - {p_t}$ 

$K = \dfrac{{2.303}}{t}\log \dfrac{{{p_i}}}{{2{p_i} - {p_t}}}$ 

Therefore, the correct option is B. 

Importance of Chemical Kinetics

This chapter is of utmost importance in the Chemistry syllabus for NEET. It introduces how a chemical reaction proceeds to attain equilibrium considering all the factors influencing the reaction. Every subtopic under the topics will be explained with proper illustration and scientific derivations.

Students will also learn the definitions, meaning, and implications of new terms in this chapter such as instantaneous rate, how to measure the rate of reaction, and how the rate depends on various factors. They will learn how the rate of a chemical reaction can be controlled by altering specific conditions such as concentration, temperature, pressure, etc.

This chapter will explain how the outcome of a chemical reaction can be intentionally driven to get a particular outcome. All these explanations will be given based on laws, theories, and scientific principles with proper mathematical derivations.

Students will also learn how to determine the order of a reaction. The examples shown in this chapter will explain what the order of a chemical reaction is and how to determine one. The use of Chemical Kinetics notes will enable students to understand the implications of all the scientific terms taught in this chapter.

This chapter is an important part of the physical chemistry syllabus that teaches how to measure the rate of a reaction and how to control it.

Benefits of Chemical Kinetics Notes for NEET

• These revision notes have been designed to offer a consolidated version of all the concepts and their specific descriptions as covered in this chapter. Students will find the scientific principles defined, derived, and explained using specific examples and mathematical expressions. Hence, these notes will be the ideal study material for revising the concepts.

• The concise format of these notes will enable NEET aspirants to revise this chapter faster before the exam.

• The easy-to-comprehend format of these notes will enable students to recall what they have studied after they are done preparing this chapter from the textbooks. It means that a NEET aspirant will be able to recall the fundamental concepts to answer a conceptual question asked in the NEET exam accurately.

Download Free Chemical Kinetics Notes PDF

These revision notes can be downloaded for free from Vedantu. You can use them as the perfect study guide to revise what you have studied in this chapter. Download and refer to the Chemical Kinetics notes for NEET PDF anytime you want to revise the chapter and resolve doubts on your own.

Other Important Links Related to NEET Chemical Kinetics

NEET Chemistry Revision Notes - Chapter Pages