NEET Chapter - Chemical Kinetics

Chemical Kinetics is a branch of chemistry concerned with the study of chemical reaction rates, as well as the factors that influence reaction rates and the process by which reactions occur. The rate of a reaction is affected by parameters such as concentration, temperature, pressure, and catalyst. At the macroscopic level, for kinetics, we are  concerned with the quantities reacted or created, as well as the speeds at which they were consumed or formed. 

This chapter is one of the easiest, most significant and scoring chapters for competitive tests like NEET, and mastering it will help you score well in the exams.

Important Topics of  Chemical Kinetics:

• Reaction Rate

• Rate Law

• Half-Life of a Reaction

• Order of Reaction

• Pseudo First Order Reaction 

• Arrhenius Equation Derivation

Important Definitions of  Chemical Kinetics:

Rate of a Chemical Reaction:

The change in concentration of a reactant or product per unit time is referred to as the rate of a reaction.

• The Average Rate of a Reaction: 

The change in the concentration of reactant or product over a definite time interval is called the average rate of reaction (rav).

For an hypothetical reaction such as:

R $\longrightarrow$ P 

Average rate of reaction (rav) = $\dfrac{Decrease~in~concentration~of~R}{Time~taken}$ 

= - $\dfrac{\Delta [R]}{\Delta t}$   

Or

= $\dfrac{Increase~in~concentration~of~P}{Time~taken}$ 

= $\dfrac{\Delta [P]}{\Delta t}$

• Instantaneous Rate of a Reaction: 

The rate of change of concentration of the reactants or products at a particular instant of time is called instantaneous rate of reaction (rinst). 

Instantaneous rate of reaction (rinst) = - $\dfrac{d [R]}{dt}$ =  $\dfrac{d [P]}{dt}$

Note:  Negative sign on the rate reaction of reactant shows decrease or disappearance of concentration of reactant.

• Unit of Rate of Reaction:

Unit of rate of reaction : concentration-1 time  =  mol L-1 s-1   or  atm s-1  

• Overall Rate of Reaction:

For a reaction:

A  +  2B  $\longrightarrow$  3C  +  4 D

Rate of reaction = - $\dfrac{\Delta [A]}{\Delta t}$  =  - $\dfrac{1}{2}$ $\dfrac{\Delta [B]}{\Delta t}$  =    $\dfrac{1}{3}$ $\dfrac{\Delta [C]}{\Delta t}$  =    - $\dfrac{1}{4}$ $\dfrac{\Delta [D]}{\Delta t}$

Factors Affecting Rate of Reaction:

Factors on which rate of reaction depends are:

• Concentration of Reactant: Rate of reaction is directly proportional to the concentration (or pressure of gas) of reactant.

• Temperature: The rate of reaction increases with the increase in temperature.

• Catalyst: There are some catalysts that increase the rate of reaction whereas there are some inhibitor catalysts that decrease the rate of reaction.

• Surface Area: The substance with greater surface area (or small size) increases the rate of reaction.

Rate Law:

As the concentration of reactants decreases, the rate of a reaction also decreases with time. Rates, on the other hand, tend to increase as the reactant concentration increases. As a result, the rate of a reaction is determined by the concentration of reactants.             

Consider a reaction:

aA  +  bB  $\longrightarrow$   cC   + dD

According to rate law,

Rate  ∝  $\left[A\right]$x $\left[B\right]$y

where, x and y may or may not be equal to stoichiometric coefficients of reactants A (a) and B i.e a and b. 

Rate = k  $\left[A\right]$x $\left[B\right]$y

- $\dfrac{d [R]}{dt}$  = k  $\left[A\right]$x $\left[B\right]$y

This equation is a differential rate equation and k is the constant of proportionality which is called the rate constant. 

In a balanced chemical equation, rate law is an expression in which reaction rate is expressed in terms of molar concentration of reactants with each term raised to a power, which may or may not be the same as the stoichiometric coefficient of the reacting species. Rate law can be determined experimentally not theoretically.

Order of a Reaction: 

For a balanced chemical reaction,

aA + bB $\longrightarrow$  cC + dD

Rate = $\left[A\right]$x $\left[B\right]$y

Order of reaction = x + y

Order of a chemical reaction is the sum of powers of the concentration of the reactants in the rate law expression. Order of reaction can be 0, 1, 2, 3…… and can be fractions too.

Unit of Rate Constant:

k  = R /  $\left[A\right]$x$\left[B\right]$y

= $\dfrac{Concentration}{time}$   X   $\dfrac{1}{(Concentration)^n}$

where, n = x + y

Integrated Rate Equation: 

• Zero Order Reaction:

For zero order reaction, the rate of the reaction is proportional to the zeroth power of concentration of reactant.

Consider the reaction,

R $\longrightarrow$ P

Rate =  - $\dfrac{d [R]}{dt}$  = k R0

Rate =  - $\dfrac{d [R]}{dt}$  = k (1)

d$\left[R\right]$  = - kdt

Integrating both sides we get,

$\left[R\right]$  =  - kt  +  I

where, I is the integration constant,

Let $\left[R\right]$0 is the initial concentration of reactant,

At t = 0,

$\left[R\right]$0  =  -k(0)  +  I

$\left[R\right]$0  =  I

By substituting the value of I in the above equation we get,

$\left[R\right]$  =  -kt  +  $\left[R\right]$0

Comparing the above equation with,

y = mx +c

y = concentration of R; slope, m = -k;  x = t;  c = $\left[R\right]$0 

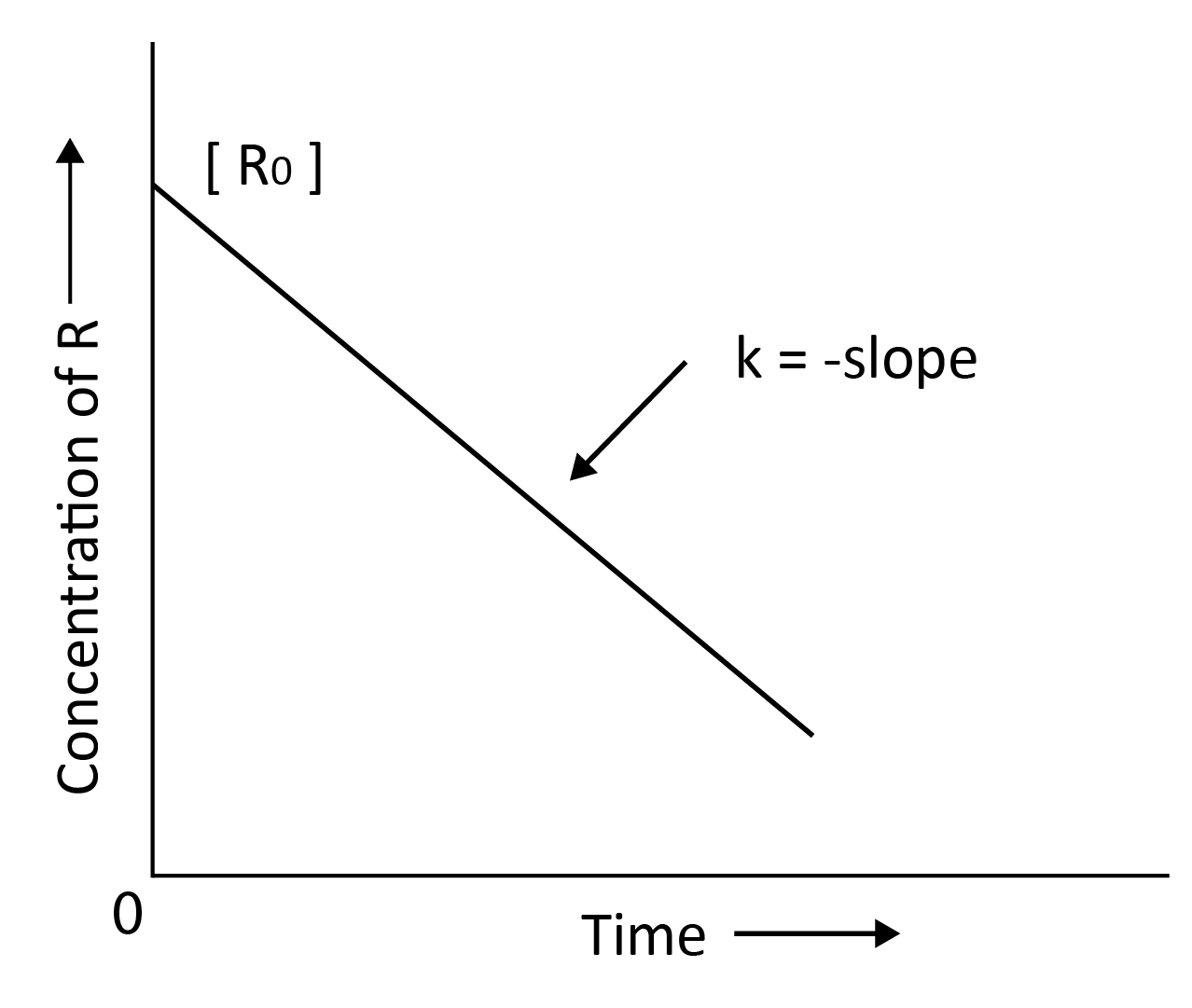
k  =  $\dfrac{[R]_0 - [R]}{t}$

Example of zero order reaction: 

• At high pressure, decomposition of gaseous ammonia on the Pt surface.

• Thermochemical breakdown of HI on gold.

• First Order Reaction:

For the first order reaction, the reaction rate is proportional to the first power of the reactant concentration.

Consider the reaction,

R $\longrightarrow$ P

Rate =  - $\dfrac{d [R]}{dt}$  = k R1

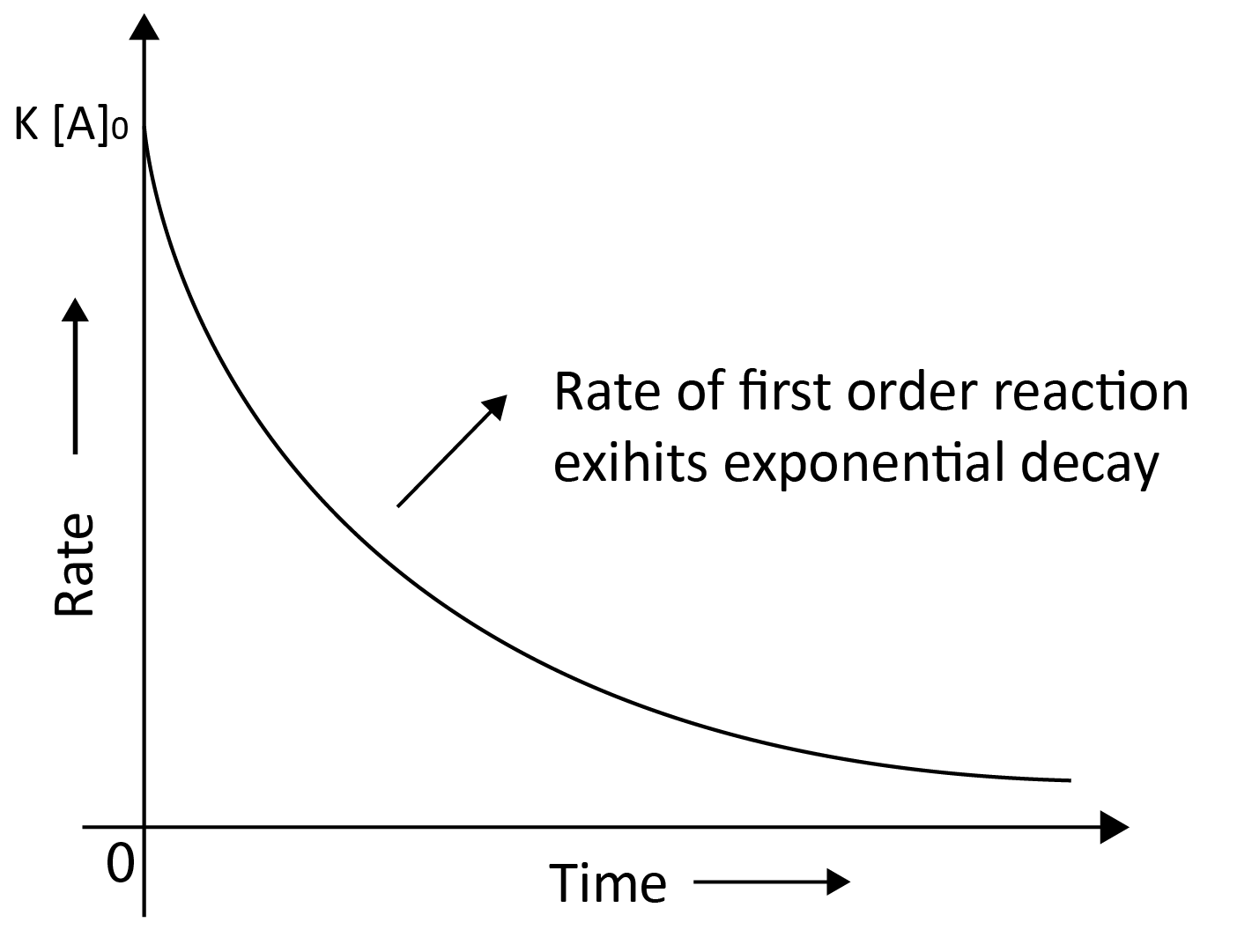
Rate =  - $\dfrac{d [R]}{dt}$  = k ($\left[R\right]$)

$\dfrac{d [R]}{[R]}$  = - kdt

Integrating both sides we get,

ln $\left[R\right]$  =  - kt  +  I

where, I is the integration constant,

Let [R]0 is the initial concentration of reactant,

At t = 0,

ln$\left[R\right]$0  =  -k(0)  +  I

ln$\left[R\right]$0  =  I

By substituting the value of I in the above equation we get,

ln$\left[R\right]$  =  -kt  +  ln$\left[R\right]$0

Comparing the above equation with,

y = mx +c

y = ln$\left[R\right]$ ; slope, m = -k;  x = t;  c = ln$\left[R\right]$0 

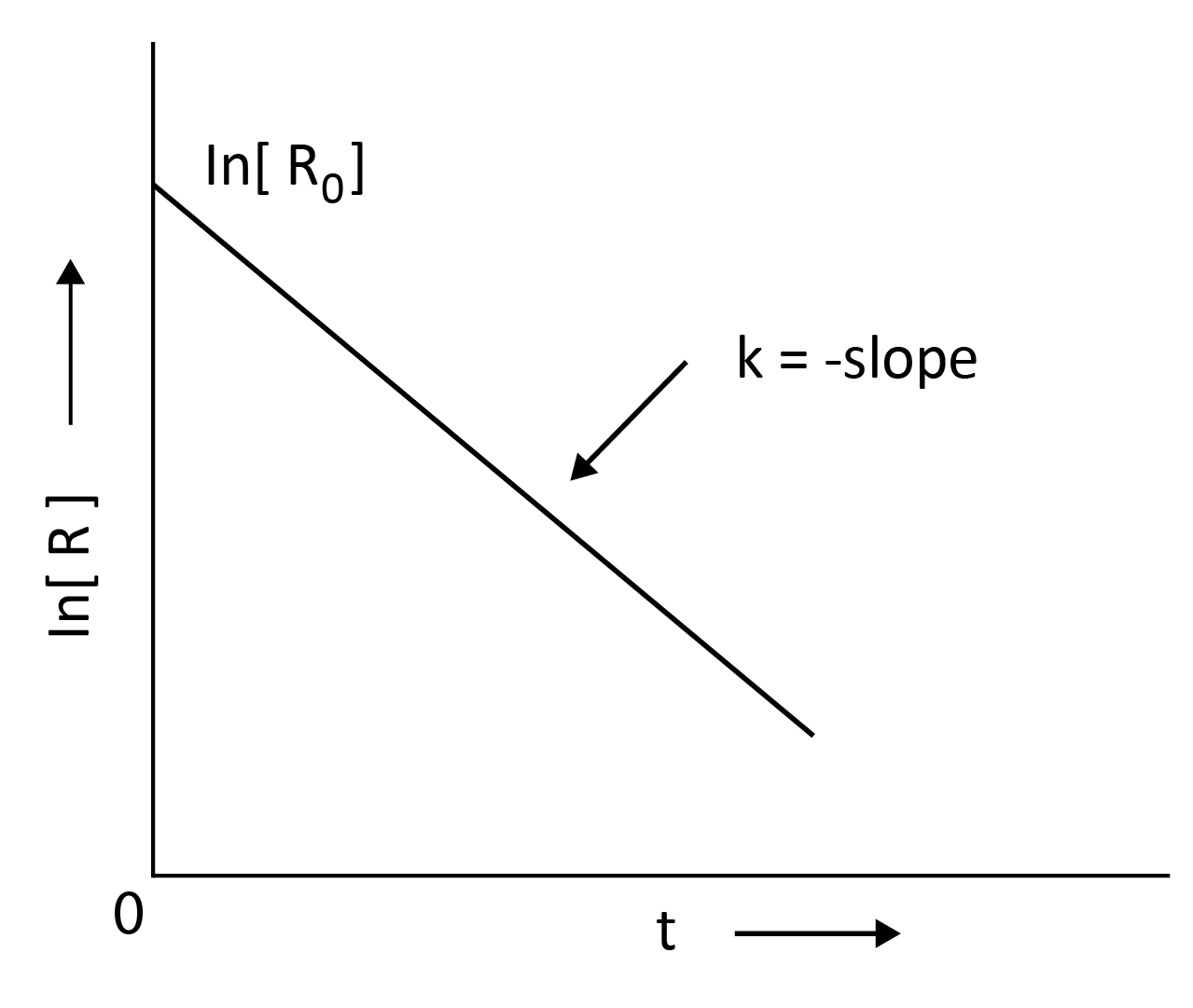
k  =  $\dfrac{ln[R]_0 - ln[R]}{t}$

k  =   $\dfrac{1}{t}$ $ln\dfrac{[R]_0 }{[R]}$

Also, 

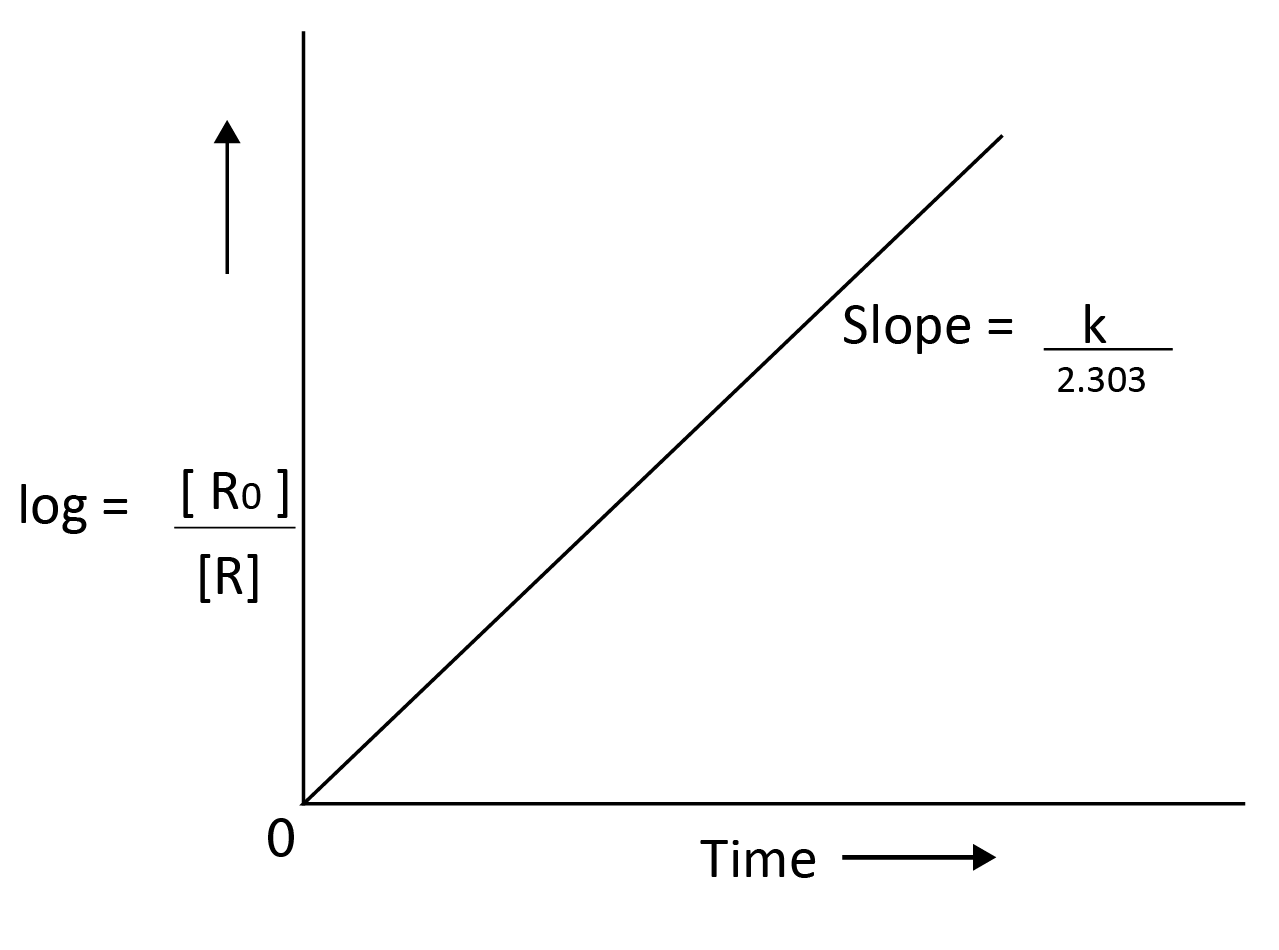
$log\dfrac{[R]_0 }{[R]}$  =   $\dfrac{kt}{2.303}$  

y = mx

y = $log\dfrac{[R]_0 }{[R]}$; slope,m = $\dfrac{k}{2.303}$ ; x = t  

Example of first order reaction: 

• Hydrogenation of ethene 

• Radioactive (artificial or natural) decay.

• Decomposition of N2O5 and NO2

Half Life:

Half life of a reaction is considered the time it takes for a reactant's concentration to reduce to half of its initial concentration. It is represent by t1/2  

• Zero Order Reaction:  

$\left[R\right]$  =  -kt  + $\left[R\right]$0

k  =   $\dfrac{[R]_0 - [R] }{t}$

At t = t ½

$\left[R\right]$ =$\left[R\right]$0/2

Therefore, 

k  =   $\dfrac{[R]_0 - ½ [R]_0 }{t_1/2}$   

t1/2 =   $\dfrac{[R]_0 - ½ [R]_0 }{k}$    =   $\dfrac{[R]_0}{2k}$

• First Order Reaction:

k   =  $\dfrac{2.303}{t}$  $log\dfrac{[R]_0 }{[R]}$  

At t = t1/2

$\left[R\right]$ = $\left[R\right]$0/2

t1/2   =  $\dfrac{2.303}{k}$  $log\dfrac{[R]_0 }{[R]_0/2}$  

t1/2   =  $\dfrac{2.303}{k}$  $log 2$  

t1/2   =  $\dfrac{2.303}{k}$  X  0.301

t1/2   =  $\dfrac{0.693}{k}$             

Conclusion of Derivations:

• For zero order reaction , t1/2  is proportional to $\left[R\right]$0 whereas for first order reaction, t1/2 is independent of $\left[R\right]$0.

• The order of reaction can be determined by the equation,

t1/2 ∝ $\left[R\right]$0n-1

where, n is the order of reaction.

Pseudo First Order Reactions: 

Under certain conditions, reactions which aren't actually first-order become first-order reactions are known as pseudo first order reactions.

Example:

• Hydrolysis of ethyl acetate with water is a pseudo first order reaction as the large amount of water required for hydrolysis, the concentration of water does not change significantly during the process. As a result, only the concentration of ethyl acetate affects the rate of the reaction. 

•  The reaction for the inversion of cane sugar is also a pseudo-first-order reaction. 

Practical Analysis of First Order Reaction:

When the components are in gaseous phase, pressure is taken instead of concentration.

Let pi be the initial pressure, x atm pressure be the decrease in the pressure of reactant A  at t time of the given reaction.

Total pressure, pt =    pi - x   +  x  +  x  =  pi + x 

x = pt - pi

pA  =  pi - x  =  pi - (pt - pi)  =  2pi - pt

The rate constant for first order reaction, for gaseous components,

k   =  $\dfrac{2.303}{t}$  $log\dfrac{p_i}{p_A}$   

k   =  $\dfrac{2.303}{t}$  $log\dfrac{p_i}{2p_i - p_t}$   

Molecularity of a Reaction:

The molecularity of a reaction refers to the number of reacting species (atoms, ions, or molecules) involved in an elementary reaction that must collide together to produce a chemical reaction.

Classification of reactions on the basis of Molecularity: 

• Unimolecular Reactions: When only one reacting species is involved in the reaction then the reaction is a unimolecular reaction.

Example: Decomposition of ammonium nitrate.

NH4NO2  $\longrightarrow$    N2  +  2 H2O

• Bimolecular Reactions: When two reacting species are involved in the reaction then the reaction is a bimolecular reaction.

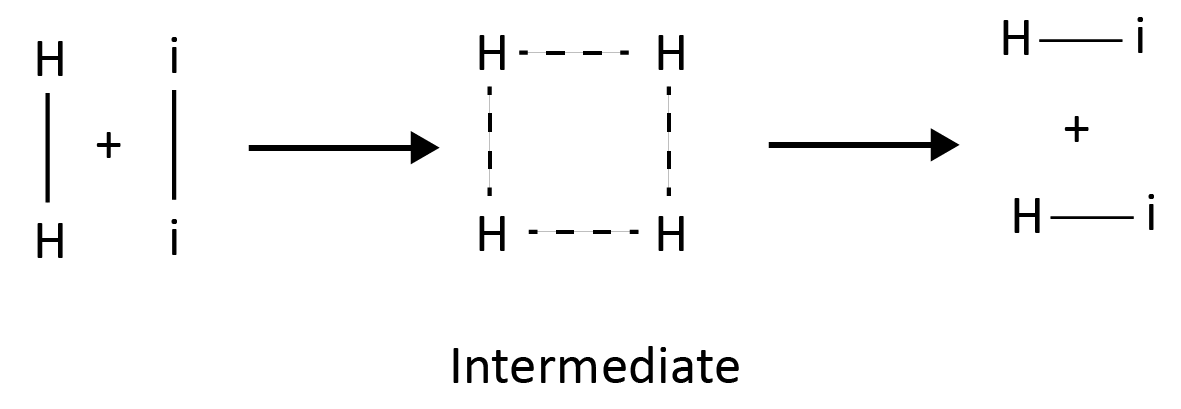
Example: Dissociation of HI involves the collision of 2 species together.

2 HI $\longrightarrow$    H2  +  I2

• Trimolecular Reactions: When three reacting species are involved in the reaction then the reaction is a trimolecular reaction.

Example: Oxidation of NO involves the collision of 3 species together.

2NO   +  O2  $\longrightarrow$    2NO2

Difference between the Order of Reaction and Molecularity of Reaction:

The overall rate of reaction is determined by the slowest step known as the rate-determining step. For the complex reaction, the order is given by the rate-determining step. The Molecularity of the slowest step is the same as the order of the overall reaction.

Temperature Dependence of Rate of Reaction:

The rate constant approximately doubles for a chemical reaction when the temperature rises by 10°.

Explanation:

If fractions of molecules are plotted against corresponding kinetic energies at a given temperature, a graph similar to the one shown is obtained. The most probable kinetic energy is represented by the peak of the curve, which indicates the kinetic energy possessed by the maximum fraction of molecules.

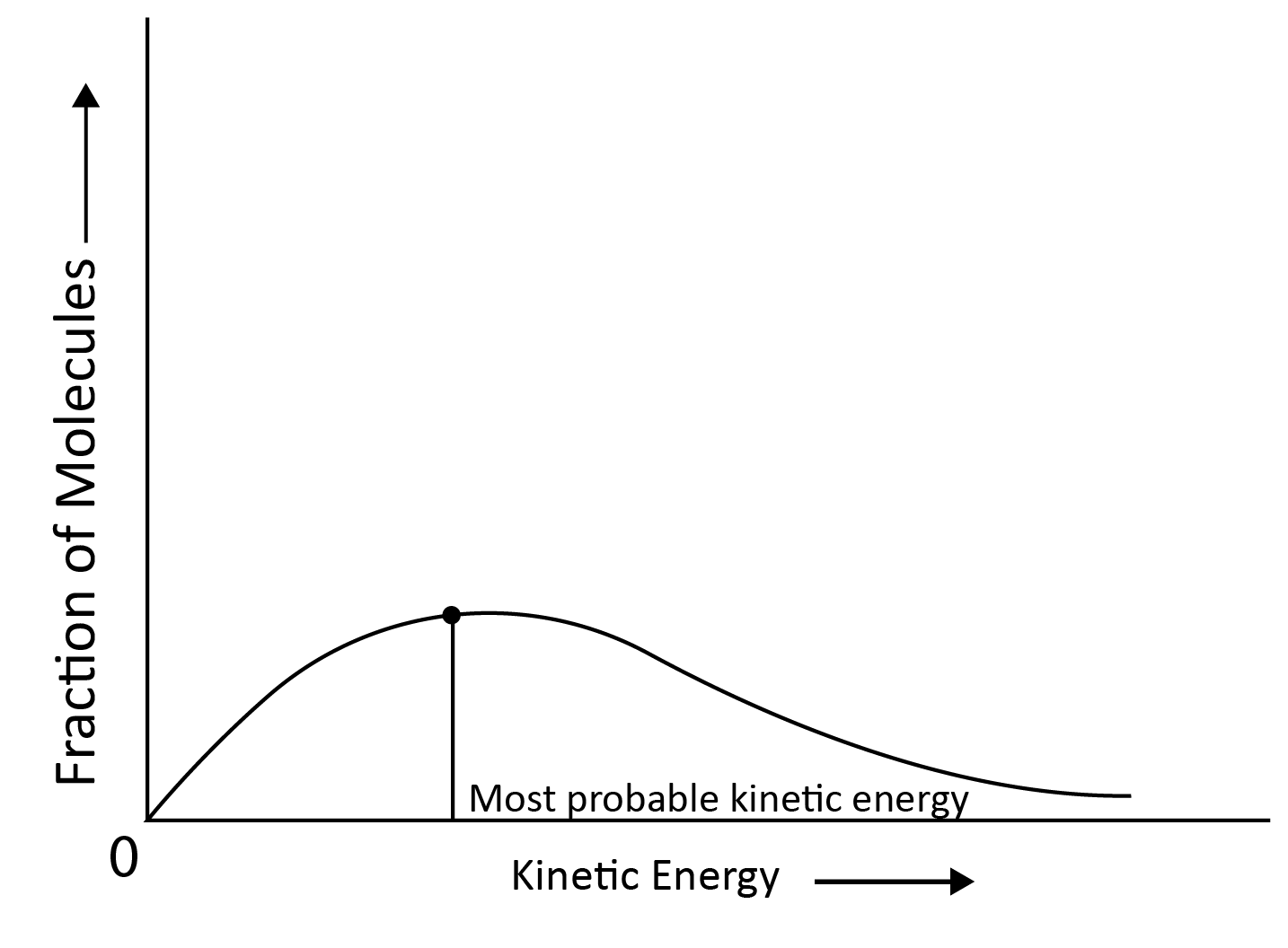
When the Temperature is Increased:

• The maximum of the curve shifts to a higher energy value, indicating that the most probable kinetic energy increases.

• The curve shifts to the right, indicating that there are more molecules with significantly higher energies.

• Since total probability must always be one, the area under the curve remains constant.

• At (t + 10) the area representing the percentage of molecules with energy equal to or greater than activation energy doubles, resulting in a reaction rate doubled.

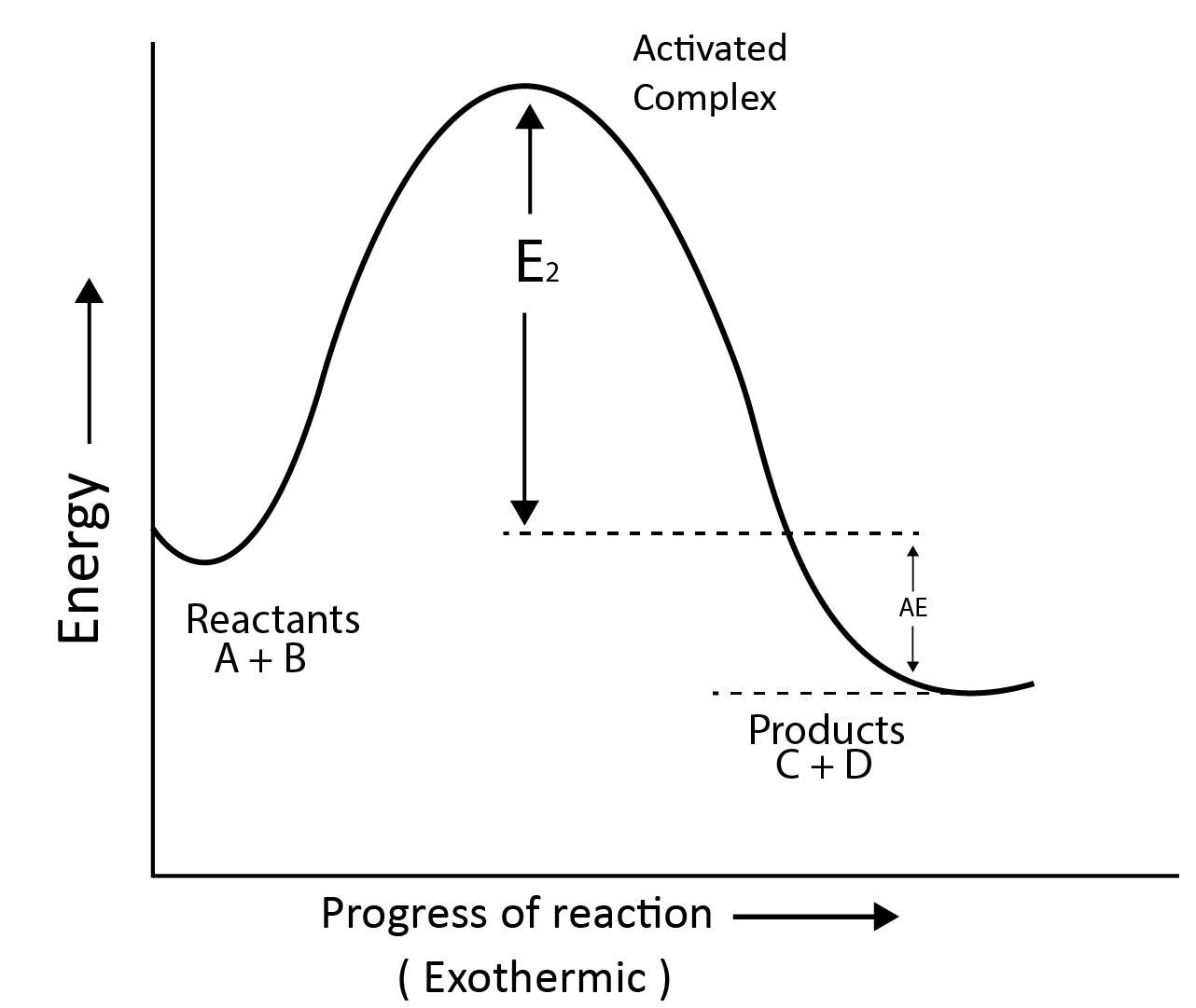
Activation Energy:  

• According to collision theory, the molecules collide with each other to carry out the reaction.

• The least amount of energy that colliding molecules must have in order for the collision to be effective is called the threshold energy.

• The activation energy is the lowest additional amount of energy absorbed by the reactant molecules so that their energy becomes equal to the threshold value.

Threshold Energy   =   Activation Energy   +   Energy possessed by reactants

Example:  

Reaction Profile for Exothermic Reactions:

A + B  $\longrightarrow$  C  + D

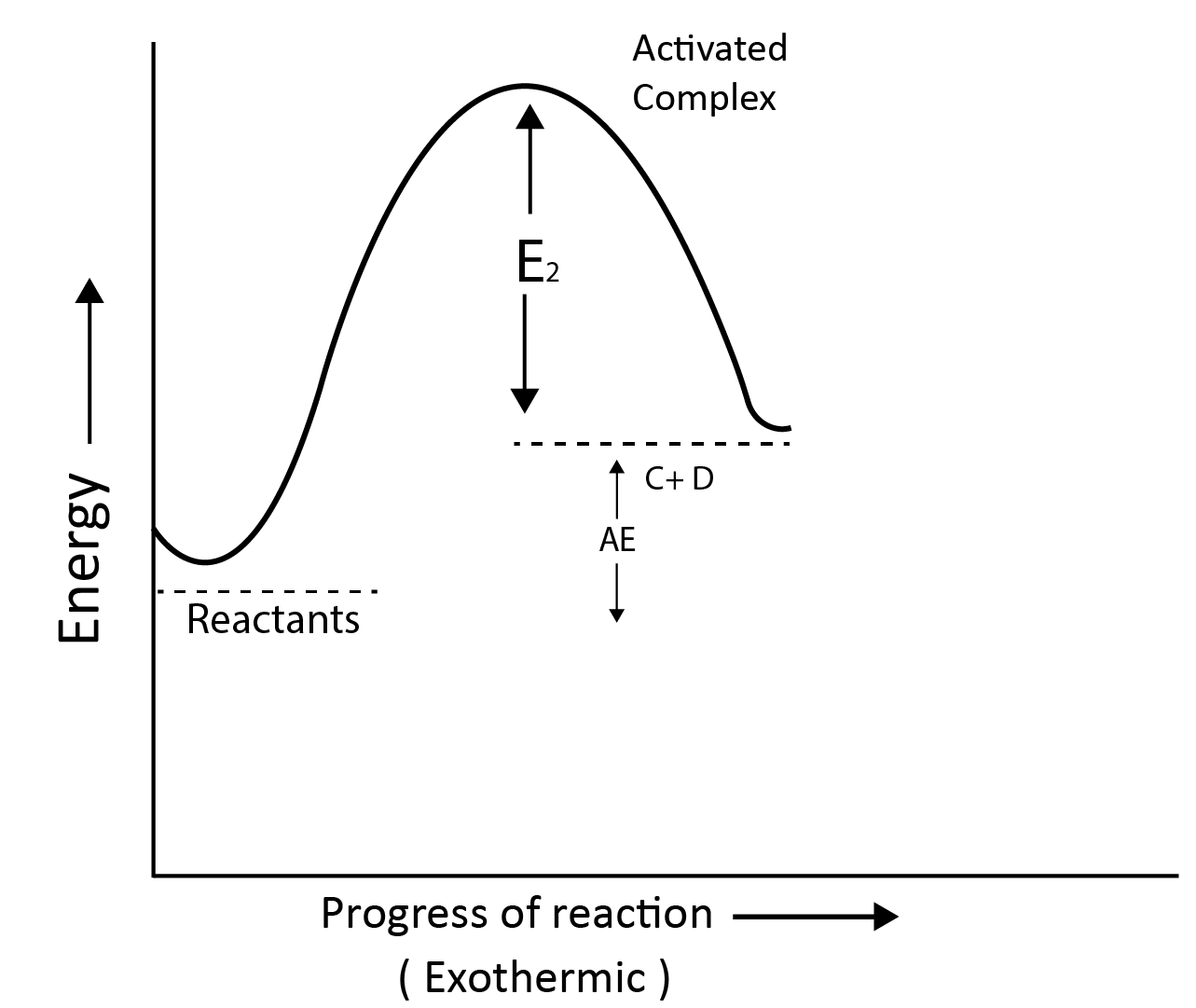
Reaction profile for endothermic reactions:

A + B  $\longrightarrow$  C  + D

• Arrhenius Equation: The Arrhenius equation can quantitatively explain the temperature dependency of the rate of a chemical process.

k = A e-Ea/RT

where,  A: Arrhenius factor or pre-exponential factor or frequency factor

R: Gas constant

Ea: Activation energy

By the Arrhenius equation, it has been observed that increasing the temperature or decreasing the activation energy causes an increase in the reaction rate and an exponential increase in the rate constant.

By taking the natural log of Arrhenius equation

ln k  =   -$\dfrac{Ea}{RT}$   +  ln A

At temperature, T(1):

ln k(1)  =   -$\dfrac{Ea}{RT(1)}$   +  ln A

ln k(2)  =   -$\dfrac{Ea}{RT(2)}$   +  ln A

Now,

ln k(2)- ln k(1)  =   $\dfrac{Ea}{RT(1)}$  -  $\dfrac{Ea}{RT(2)}$ 

$\ln\dfrac{k(2)}{k(1)}$    =    $\dfrac{Ea}{R}$ $\left[ \dfrac{1}{T(1)} -  \dfrac{1}{T(2)} \right]$

$\log\dfrac{k(2)}{k(1)}$    =    $\dfrac{Ea}{2.303R}$ $\left[ \dfrac{1}{T(1)} -  \dfrac{1}{T(2)} \right]$

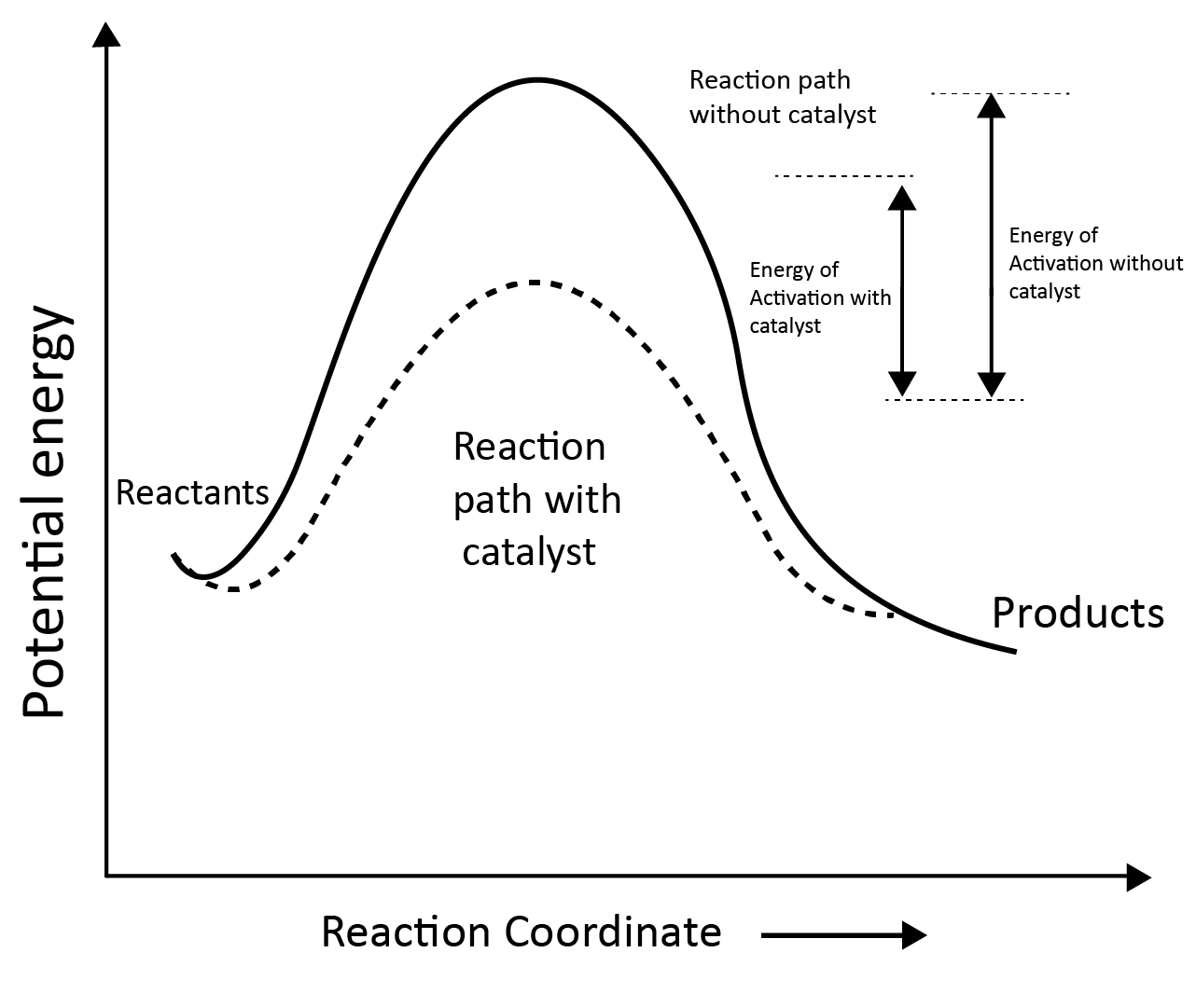
Effect of Catalyst:

According to the intermediate complex theory, reactants first react with the catalyst to generate an intermediate complex, which subsequently decomposes into products, regenerating the catalyst.

Effect of catalyst on activation energy: 

Catalysts give an alternative pathway by lowering the potential energy barrier by reducing the activation energy between reactants and products.

Solved Examples from the Chapter

Example 1: NO2 required for a reaction is produced by the decomposition of N2O5 in CCI4 as per the equation, 

2N2O5(g)   $\longrightarrow$   4NO2(g) + O2(g). 

The initial concentration of N2O5 is 3.00 mol L-1 and it is 2.75 mol L-1 after 30 minutes.

The rate of formation of NO2 is :  : 

1. 2.083  X 10 -3 mol L-1 min-1

2. 8.333  X 10 -3 mol L-1 min-1

3. 4.167  X 10 -3 mol L-1 min-1

4. 1.667  X 10 -2 mol L-1 min-1

Solution: (d) Rate of disappearance of N2O5 =  - $\dfrac{\Delta [N_2O_5]}{\Delta t}$                                                                 =   -  $\dfrac{2.75 -3}{30}$  =   $\dfrac{1}{120}$  mol L-1 min-1

Rate of formation of NO2:   

-$\dfrac{1}{2}$ $\dfrac{\Delta [N_2O_5]}{\Delta t}$    =   $\dfrac{1}{4}$ $\dfrac{\Delta [NO_2]}{\Delta t}$  

⇒                            $\dfrac{\Delta [NO_2]}{\Delta t}$   =   $\dfrac{1}{120}$   X  $\dfrac{4}{2}$   =   0.01667  =   1.667  X  10 -2 mol L-1 min-1

Key points: For a reaction:

A  +  2B  $\longrightarrow$  3C  +  4 D

Rate of reaction = - $\dfrac{\Delta [A]}{\Delta t}$  =  - $\dfrac{1}{2}$ $\dfrac{\Delta [B]}{\Delta t}$  =    $\dfrac{1}{3}$ $\dfrac{\Delta [C]}{\Delta t}$  =    - $\dfrac{1}{4}$ $\dfrac{\Delta [D]}{\Delta t}$

Example 2: For the reaction of H2 with I2, the rate constant is 2.5 x 10-4 dm3 mol-1s-1 at 327°C and 1.0 dm3 mol-1 at 527°C. The activation energy for the reaction, in kJ mol-1 is : (R = 8.314 J K-1 mol-1 ) 

1. 59

2. 166

3. 72

4. 150

Solution:  (b)Given,   T(1)  =  327 + 273  = 600 K

T(2)  =  527 +  273 =  800 K

k(1)    =   2.5 x 10-4 dm3 mol-1s-1

k(2)    =   1 dm3 mol-1s-1

We know, $\log\dfrac{k(2)}{k(1)}$    =    $\dfrac{Ea}{2.303R}$ $\left[ \dfrac{1}{T(1)} -  \dfrac{1}{T(2)} \right]$

$\log\dfrac{1}{2.5 \times 10^{-4}}$    =    $\dfrac{Ea}{2.303 \times 8.314}$ $\left[ \dfrac{1}{600} -  \dfrac{1}{800} \right]$

Ea = 166 KJ mol-1

Key points: 

$\log\dfrac{k(2)}{k(1)}$    =    $\dfrac{Ea}{2.303R}$ $\left[ \dfrac{1}{T(1)} -  \dfrac{1}{T(2)} \right]$

Solved Questions from the Previous Year Question Papers

Question 1: When initial concentration of the reactant is doubled, the half-life period of a zero order reaction 

1. is halved 

2. is doubled 

3. is tripled 

4. remains unchanged. 

Solution: (b)  is doubled 

We know that, for zero order reaction,

t1/2   =  $\dfrac{[R]_0}{2k}$

t1/2    ∝ $\left[R\right]$0

As the  initial concentration of the reactant is doubled, the half-life period of a zero order reaction is also doubled.

Question 2: The rate constant for a first order reaction is 4.606 x 10-3 s-1. The time required to reduce 2.0 g of the reactant to 0.2 g is : 

1. 200 s 

2. 500 s 

3. 1000 s 

4. 100 s 

Solution: (a) 

Given, k   =   4.606 x 10-3 s-1

$\left[R\right]$0    =  2 g

$\left[R\right]$   =    0.2 g

We know of first order reaction,

k    =    $\dfrac{2.303}{t}$ $log\dfrac{[R]_0 }{[R]}$  

4.606 x 10-3  =   $\dfrac{2.303}{t}$ $log\dfrac{2}{0.2}$  

t    =    500 s

Question 3: For the chemical reaction N2(g) + 3H2(g) ⇌  2NH3(g) the correct option is:

(a) -$\dfrac{d [N_2]}{d t}$  =   $2 \dfrac{d[NH_3]}{dt}$ 

(b) -$\dfrac{d [N_2]}{d t}$  =  $\dfrac{1}{2}$   $\dfrac{d[NH_3]}{dt}$ 

(c) $3\dfrac{d [H_2]}{d t}$  = 2   $\dfrac{d[NH_3]}{dt}$ 

(d) -$\dfrac{1}{3}$ $\dfrac{d [H_2]}{d t}$  =  -$\dfrac{1}{2}$   $\dfrac{d[NH_3]}{dt}$ 

Solution:  (b) -$\dfrac{d [N_2]}{d t}$  =  $\dfrac{1}{2}$   $\dfrac{d[NH_3]}{dt}$ 

For, chemical reaction,

N2(g) + 3H2(g) ⇌  2NH3(g) 

Rate of reaction will be,

Rate   =   - $\dfrac{d [N_2]}{d t}$  =  -$\dfrac{1}{3}$   $\dfrac{d[H_2]}{dt}$   =  $\dfrac{1}{2}$   $\dfrac{d[NH_3]}{dt}$ 

Practice Questions

Question 1: For a reaction of order n, the unit of the rate constant is : 

1. mol 1-n  L 1- n s 

2. mol 1-n  L 2n s -1

3. mol 1-n  L n-1 s -1

4. mol 1-n  L 1- n s-1 

Answer: (c) mol 1-n  L n-1 s -1

Question 2: The rate of a certain biochemical reaction at physiological temperature (T) occurs 106 times faster with enzyme than without. The change in the activation energy upon adding enzyme is :

1. + 6 RT

2. - 6(2.303) RT

3. - 6 RT

4. + 6(2.303) RT

Answer: (b)  - 6(2.303) RT

Conclusion:

In this article, we get to know how to know the rate at which the reaction is carried out. The factors that affect the rate of reaction and how to increase or decrease the rate of reaction. In this article, the conditions such as the time at which half of the reactant is achieved. The graphs based on the order of the reaction is also presented in the article which helps the student to work with the practical or mathematical derived equations.