Revision Notes on Some Basic Concepts of Chemistry for NEET 2024

Physical quantities and SI units

The use of the international system of units was proposed during the 11th general conference of weights and measures in 1960. SI Units is an abbreviation for Standard International Units (after the French expression La System International de units).

Fundamental units:

The SI system has seven basic physical units, which are as follows:

Derived Units: Derivative units are those that are created by combining basic units, such as velocity, which is expressed as distance/time. As a result, the unit is m/s or ${\rm{m}}{{\rm{s}}^{{\rm{-1}}}}{\rm{.}}$

The following are some examples of derived units:

Precision and Accuracy:

Precision: It's the similarity of different measurements for the same quantity.

Accuracy: It is the agreement between a given value and the true value.

Assume that a substance's real weight is 3.00g. The following are the measurements reported by three students:

• Case of A student: It is precision but no accuracy because measurements one close but not accurate.

• Case of B student: Measurements are close (precision) and accurate (accuracy).

• Case of C student: Measurement are not close (no precision) and not accurate (no accuracy)

Stoichiometry: It is the measurement of reactant and product masses or volumes in a chemically balanced reaction. Consider the reaction of ammonia formation.

All of the gases are denoted by a letter (g), and the stoichiometric coefficients are 3 for ${{\rm{H}}_{\rm{2}}}$ and 2 for ${\rm{N}}{{\rm{H}}_{\rm{3}}}{\rm{.}}$ Ammonia formation can be viewed in a variety of ways:

• Two moles of ${\rm{N}}{{\rm{H}}_{{\rm{3}}\left( g \right)}}$ are formed when one mole of ${{\rm{N}}_{{\rm{2}}\left( g \right)}}$ interacts with three moles of ${{\rm{H}}_{{\rm{2}}\left( g \right)}}.$

• 28g of ${{\rm{N}}_{{\rm{2}}\left( g \right)}}$ combines with 6 g of ${{\rm{H}}_{{\rm{2}}\left( g \right)}}$ to produce 34 g of ${\rm{N}}{{\rm{H}}_{{\rm{3}}\left( g \right)}}.$

• 22.4 litres of ${{\rm{N}}_{{\rm{2}}\left( g \right)}}$ react with 67.2 litres of ${{\rm{H}}_{{\rm{2}}\left( g \right)}}$ to produce 44.8 litres of ${\rm{N}}{{\rm{H}}_{{\rm{3}}\left( g \right)}}.$

Significant figures:

A substance's weight of 7.52g implies that it is accurate to the hundredth of a gram and can be represented as $7.52{\rm{ }} \pm {\rm{ }}0.01.$ It signifies that the tiniest deviation may occur at the second decimal point, or that the uncertainty is ${\rm{ \pm  0}}{\rm{.01 g}}{\rm{.}}$

Consider the mass of 6.4234 g. $6.4234 \pm 0.001{\rm{ g}}$is the right representation.

In the first situation, the weight has three significant numbers, whereas in the second case, the weight has five significant figures.

1. Significance of Zero: It is not a significant quantity if zero is used to find the decimal point. As a result, there are only two significant digits in 0.0072, whereas there are four significant figures in 70.40 since zero comes after four. Again, there are two significant figures in 0.0070, because zero after 7 is significant because it has a significance in exponentials. When we compare ${\rm{7}}{\rm{.0}} \times {\rm{1}}{{\rm{0}}^{{\rm{--3}}}}{\rm{ and 7}} \times {\rm{1}}{{\rm{0}}^{{\rm{--3}}}}{\rm{,}}$  the first has a one-in-seventy uncertainty and the second has a one-in-seven uncertainty. The number of significant figures is not increased by the exponential term.

2. Addition and Subtraction of Quantities: In this scenario, the result's uncertainty is equal to the sum of the individual quantities' uncertainties.

3. Multiplication and Division: In this scenario, the result's uncertainty is equal to the total of the individual uncertainties' percentages.

4. Rounding Off: The following guidelines are followed:

• If the digit following the last digit to be kept is less than 5, the last digit is kept. 1.752 = 1.75, for example (2 is less than 5).

• If the digit after the final number to be kept is greater than 5, the digit to be kept is increased by one. For example, 1.756 = 1.76. (6 is more than 5).

• If the digit after the last digit to be kept equals 5, the last digit is kept if it is even and increased by one if it is odd.

5. Calculations Involving Addition and Subtraction: 

When adding and subtracting, the final result should have the same number of decimal places as the number with the least number of decimal places.

6. Calculations Involving Multiplication and Division: 

The final result should have the same number of significant digits as the number with the least significant digits in this example.

Matter and Its Nature:

Matter is defined as anything that has mass and occupies space. There are three states of matter as shown below,

1. Solid

2. Liquid

3. Gas

Solid and Its Basic Properties

The following are the properties of solids:

• It has a definite shape (rigid) and definite volume.

• Particles are vibrated along set axes.

Liquid and Its Basic Properties

The following are the properties of liquids:

• There is no particular shape (takes the shape of its container)

• It has a specific volume.

• Although particles are free to move over one another, they remain attracted to one another.

Gas and Its Basic Properties

The following are the properties of gases:

• There is no particular shape (takes the shape of its container).

• There is no definite volume.

• Highly compressible particles travel at random with little or no attraction to one another.

Comparison of Gases, Liquids and Solids

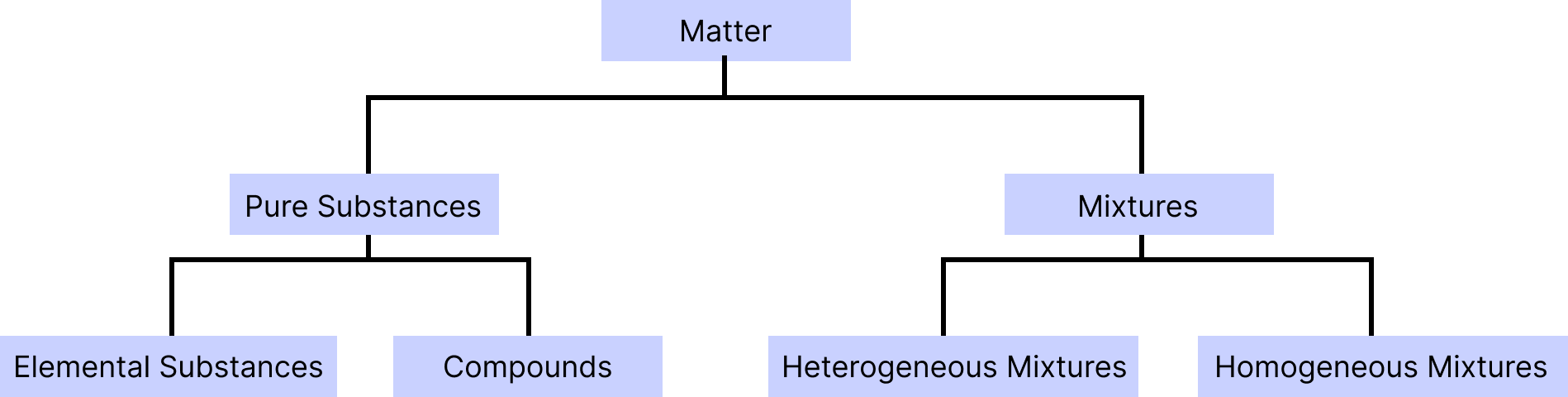
Matter

Pure substances: Matter with an invariant chemical composition and distinct properties is termed as pure substance. For example, glucose, gold and water. It is classified into two forms: elements and compounds.

1. Element: It is one of the most fundamental compounds, consisting of only one type of atom and incapable of being split into smaller substances by conventional chemical methods. For example: hydrogen, carbon etc.

2. Compound: When two or more than two atoms of different elements are combined together by chemical bonds in a definite proportion, a chemical compound is formed. For example, NaCl and baking soda.

Mixture: When a material is made up of two or more different pure substances, which may be present in it in any ratio in the form of suspension, solution or colloid is known as mixture. For example, tea and sugar solution.

1. Homogenous Mixture: The components of the mixture are uniform throughout. They have the same properties and composition. For example, salt in water.

2. Heterogenous Mixture: A heterogeneous mixture is a non-uniform combination having two or more elements with big enough quantities of each component to be detected, though magnification may be required. For example: oil and water mixture and soils.

Separation of Mixtures: The following method can be used to separate mixtures into constituents:

• Filtration can separate mixtures in which one component is soluble in one solvent but not in another.

• Distillation is a technique for separating elements of mixtures with various boiling points.

• Extraction dissolves one of the mixture's components.

• The process of crystallization is the separation of solids with varying solubilities in a given solvent.

• Volatile solids that sublime when heated are separated from non-volatile solids through sublimation.

• Chromatography is a technique for separating constituents of a mixture that makes use of the property of adsorption difference on a certain adsorbent.

• Different densities of constituents are separated via gravity separation.

• Magnetic separation can be used to separate magnetic and non-magnetic components.

Physical and Chemical Change: A physical change is one that does not affect chemical composition or molecular structure, while a chemical change is one that alters chemical composition and molecular structure.

1. Chemical combination is the reaction of two or more elements or compounds to produce a single product.

2. Displacement refers to the substitution of one chemical species for another.

3. Decomposition is the process of breaking down a chemical into two or more components.

${\rm{CaC}}{{\rm{O}}_{\rm{3}}} \to {\rm{CaO}} + {\rm{C}}{{\rm{O}}_{\rm{2}}}$

4. A complete and rapid oxidation of a substance is referred to as combustion.

5. Neutralisation is the reaction between an acid and a base that results in the formation of a salt.

${\rm{HCl}} + {\rm{NaOH}} \to {\rm{NaCl}} + {{\rm{H}}_{\rm{2}}}{\rm{O}}$

6. Polymerisation is the process of combining molecules of the same or distinct substances to form a single polymer molecule.

7. In the presence of visible or ultraviolet light, photochemical reactions occur.

8. When two salt solutions are mixed, double breakdown or metathesis occurs, resulting in the exchange of oppositely charged ions.

9. Hydrolysis is the process of combining salts and water to produce acidic or basic solutions.

Laws of Chemical Combinations

The quantitative study of chemical changes reveals that the chemical combination of components to produce compounds is governed by a set of basic laws known as chemical combination laws.

Law of Conservation of Mass: 

• During a chemical reaction, this law establishes the relationship between the masses of reactants and products. A. Lavoisier proposed this law in 1750.

• According to this law, "the total mass of the products during any physical or chemical change is equal to the total mass of the reactants." 

• In other words, the mass is neither created nor destroyed during a chemical reaction in an isolated system. It can only be transformed from one form to another. 

• Burning of wood is an example of conservation of mass. 

Law of Definite Proportions:

• Joseph Proust, a French chemist, stated this law. 

• According to this law, "a sample of a pure chemical compound always consists of the same elements combined together in the same definite proportions by mass, regardless of its source."

• For example, water analysis (taken from various locations such as rivers, falls, and wells) reveals that the ratio of hydrogen to oxygen in each sample of water is 2: 16 or 1: 8 by mass.

Law of Multiple Proportions:

John Dalton proposed this law. “An element may form more than one compound with another element,” it says. The masses of other elements (in two or more compounds) come in the ratio of small integers for a given mass of an element.”

For example, in ammonia $\left( {{\rm{N}}{{\rm{H}}_{\rm{3}}}} \right),$14 g of nitrogen requires 3 g of hydrogen and in hydrazine $\left( {{{\rm{N}}_{\rm{2}}}{{\rm{H}}_{\rm{4}}}} \right),$14 g of nitrogen requires 2 g of hydrogen.

As a result, a fixed mass of nitrogen necessitated 3 : 2 hydrogen in two distinct compounds (3 : 2 is a simple ratio). As a result, this follows from the "law of multiple proportions."

Law of Reciprocal Proportions:

Richter proposed this law in 1972. This is referred to as the law of equivalent proportions or the law of combining weights. According to this law, "when two different elements combine separately with the same weight of a third element, the ratio in which they combine will be the same or some simple multiple of the ratio in which they combine."

For example: Carbon dioxide $\left( {{\rm{C}}{{\rm{O}}_{\rm{2}}}} \right)$ and sulfur dioxide $\left( {{\rm{S}}{{\rm{O}}_{\rm{2}}}} \right)$ is produced when carbon and sulfur react separately with oxygen (the third element).

Also, they react together to form carbon disulfide $\left( {{\rm{C}}{{\rm{S}}_{\rm{2}}}} \right).$

Now, in carbon dioxide, 12 parts of carbon are combined with 32 parts of oxygen, and in sulphur dioxide, 32 parts of sulphur are combined with 32 parts of oxygen. The mass ratio of carbon and sulfur when combined with a fixed mass (32 parts) of oxygen is 12 : 32, that is, 3 : 8. Whereas in carbon disulphide,12 parts of carbon react with 64 parts of sulphur. As a result, the mass ratio of carbon and sulfur that combines to form carbon disulfide is 12 : 64, that is, 3 : 16.

Both the ratios are related together as follows,

3 : 8 and 3 : 16, that is, 3 : 3 and 8 : 16 or 1 : 2

This shows the law of reciprocal proportions.

Gay Lussac’s Law of Combining Volumes: 

Gay-Lussac proposed this legislation. This law governs the relationship between reactant and product volumes during chemical reactions.

This law states that "whenever gases react together under the same conditions of temperature and pressure, the volume of the reacting gases as well as products bears a simple whole number ratio."

In a chemical reaction, when gases combine, the ratio between the volume of reactants and products can be expressed in the simplest whole number. For example, when hydrogen reacts with chlorine, it produces hydrogen chloride. 

$\mathrm{H}_{2}+\mathrm{Cl}_{2} \rightarrow 2 \mathrm{HCl}$

1vol.   1vol.   2vol.

So, the ratio between the volume of hydrogen, chlorine and hydrogen chloride is 1 : 1 : 2, respectively.

Avogadro's Law:

"Equal quantities of all gases, at equivalent temperatures and pressures, contain an equal number of molecules," it says. 

The following are some examples of applications: 

• Deducing the atomicity of elementary gases.

• Determining the link between molecular mass and vapour density. 

• Determining the formula of substances. 

• Determining the molecular weight of a gas.

Atom

An atom is the smallest particle of an element that can participate in a chemical reaction.

The radius of an atom is measured in nanometers.

$\operatorname{lnm}=\dfrac{1}{10^{9} \mathrm{~m}}$

$1 \mathrm{~m}=10^{9} \mathrm{~nm}$

The hydrogen atom is the tiniest of all atoms. The radius of the hydrogen atom is ${\rm{0}}{\rm{.037}} \times {\rm{1}}{{\rm{0}}^{{\rm{ - 9}}}}{\rm{.}}$

Molecule:

Molecules are the tiniest particles of a substance that can exist on their own. It can be further classified as:

1. Homoatomic Molecules: These are molecules of the same element, and can be further classified monoatomic, diatomic, and polyatomic molecules, depending on the number of atoms. 

For example,${\rm{He, }}{{\rm{O}}_{\rm{2}}}{\rm{, }}{{\rm{P}}_{\rm{4}}}$ and so on.

2. Heteroatomic Molecule: Compound molecules are heteroatomic molecules. They come in two varieties: diatomic and polyatomic. 

For example: ${{\rm{H}}_{\rm{2}}}{\rm{O, PC}}{{\rm{l}}_{\rm{5}}}{\rm{, }}{{\rm{H}}_{\rm{2}}}{\rm{S}}{{\rm{O}}_{\rm{4}}}{\rm{, NO,}}$ and so on.

Atomic Mass Unit:

A mass equal to one twelfth the mass of a carbon-12 atom is defined as an atomic mass unit.

Average Atomic Mass:

The sum of the masses of isotopes of an element multiplied by their respective natural abundances is known as average atomic mass. The average atomic mass is formulated as:

${\rm{Average atomic mass}} = \sum\limits_{i = 1}^n {\left( {{\rm{mas}}{{\rm{s}}_i}} \right)} \left( {{\rm{abundanc}}{{\rm{e}}_i}} \right)$

Molecular Mass:

The total of the atomic masses of the atoms in a molecule is the molecule's molecular mass.

Gram Atomic Mass:

The mass of one mole of atoms of a certain element is defined as the gram atomic mass of that element.

${\rm{No}}{\rm{. of Gm}} - {\rm{atoms of element}} = \dfrac{{{\rm{Mass of element in gram}}}}{{{\rm{Gram atomic mass of element}}}}$

Gram Molecular Mass:

That amount of substance whose mass in grams is equal to its molecular mass or the equivalently molecular mass of a substance expressed in grams is called gram molecular mass. Gram molecular mass is also called one gram molecule. Thus

${\rm{No}}{\rm{. of Gm}} - {\rm{molecules of element}} = \dfrac{{{\rm{Mass of element in gram}}}}{{{\rm{Gram molecular mass of element}}}}$

Percentage Composition:

The ratio of each element's amount to the total amount of individual components contained in the compound multiplied by 100 is the percentage composition of a compound. The quantity is expressed in grams of the various elements present.

Percentage Composition of Elements in the Molecule:

${\rm{Mass \%  of element  =  }}\dfrac{{{\rm{Mass of that element}}}}{{{\rm{Molar mass of compound}}}} \times 100$

Empirical and Molecular Formulae

• Definition of Empirical Formula: It is defined as the positive integer ratio of atoms present in the compound. For instance, nitrogen dioxide has an empirical formula of ${\rm{N}}{{\rm{O}}_{\rm{2}}}$.

• Definition of Molecular Formula: The molecular formula specifies the number of different sorts of atoms in a compound’s molecule. For example: the molecular formula of nitrogen dioxide is ${{\rm{N}}_{\rm{2}}}{{\rm{O}}_{\rm{4}}}$.

Relation Between Empirical Formula and Molecular Formula

The relation between empirical formula and molecular formula can be represented as,

${\rm{Molecular formula }} = {\rm{ }}n{\rm{ }} \times {\rm{Empirical formula}}$

Calculation of Empirical Formula From Percentage Composition

Take the percentages of the atoms and divide them by the atomic mass of the atoms. You will get the values after dividing. Divide all of the values by the lowest one and you will get a ratio which is the empirical formula.

Calculation of Molecular Formula From Percentage Composition

Take the percentages of the atoms and divide them by the atomic mass of the atoms. You will get the values after dividing. Divide all of the values by the lowest one and you will get a ratio which is the empirical formula. Now, use the relation between empirical formula and molecular formula in order to calculate the molecular formula.

Chemical Equation:

It's the equation that represents chemical change in terms of reactant and product formulas.

1. A skeleton equation is an equation that has not been equalised in terms of the number of atoms in the reactants and products.

2. A balanced equation has the same amount of atoms of different sorts on both sides.

Important Terms:

1. Mass Percentage (%w/w): 

“It denotes the mass of a component in 100 g of solution.”

${\rm{Mass \%  of a component}} = \dfrac{{{\rm{ Mass of component in the sol}}{\rm{. }}}}{{{\rm{ Total Mass of sol}}{\rm{. }}}} \times 100$

2. Volume Percentage (%v/v): 

"It represents the volume of a component in a solution of $100\;{\rm{ mL}}{\rm{.}}$"

${\rm{Volume \%  of a component}} = \dfrac{{{\rm{ Volume of component }}}}{{{\rm{ Total Volume of sol}}{\rm{. }}}} \times 100$

3. Mass by Volume Percentage (% w / v): "It denotes the mass of the solute in grams in $100\;{\rm{mL of solution}}$."

${\rm{Mass by vol}}{\rm{. percent}} = \dfrac{{{\rm{ Mass of solute in g}}}}{{{\rm{ Vol}}{\rm{. of sol}}{\rm{. in mL}}}} \times 100$

4. Parts Per Million (ppm): 

${\rm{Parts per million}} = \dfrac{{{\rm{ No}}{\rm{. of parts of the component }}}}{{{\rm{ Total no}}{\rm{. of all the components of sol}}{\rm{. }}}} \times {10^6}$

Mass to mass, volume to volume, and mass to volume are all ways to express concentration in parts per million.

5. Mole Fraction (x): 

"It denotes the number of moles of a solute in one mole of solution."

${\rm{Mole fraction}} = \dfrac{{{\rm{ No}}{\rm{. of molos of the component }}}}{{{\rm{ Total no}}{\rm{. of moles all the components }}}}$

If the amount of moles of A and B in a binary mixture is ${n_{\left\{ {\rm{A}} \right\}}}{\rm{ and }}{n_{\left\{ {\rm{B}} \right\}}},$ respectively, the mole fraction of ${\rm{A}}$ will be

${x_A} = \dfrac{{{n_A}}}{{{n_A} + {n_B}}}$

6. Molarity, M: 

"It represents the number of moles of solute in 1 litre of solution."

${\rm{Molarity}},M = \dfrac{{{\rm{ Moles of solute }}}}{{{\rm{ Vol}}{\rm{. of sol in L}}}}$

Molarity is measured in milligrams per litre and is denoted by the letters ‘${\rm{M}}$' or 'Molar.' 

"The density of a solution is its mass per unit volume."

Density, $d=\dfrac{\text { Mass of sol. }}{\text { Vol. of sol. }}$

$d=\dfrac{m}{V}$

7. Molality, m: 

“It denotes the number of moles of solute present per kilogram of solvent.”

${\rm{ Molality, }}m = \dfrac{{{\rm{ Moles of solute }}}}{{{\rm{ Mass of solvent in kg}}}}$

Molality is measured in mol/kg, which can also be written as 'm' or 'molal.'

8. Normality, N: 

It denotes the number of solute equivalents in 1 litre of solution.

$\text { Normality, } N=\dfrac{\text { No. of Equivalents of solute }}{\text { Vol. of sol. in L }}$

$\text { No. of equivalents, eq }=\dfrac{\text { Weight }(W)}{\text { Equivalent weight }(E)}$

$\left.E=\dfrac{M}{z} \text { (Z is the valency factor }\right)$

9. Formality, F:

It is defined as the number of gram formula mass of ionic solute divided by the volume of solution in 1 litre.

${\rm{Formality}} = \dfrac{{{\rm{Mass of solute}}\left( {\rm{g}} \right)}}{{{\rm{Volume of solution}}\left( {{\rm{litre}}} \right) \times {\rm{gram formula mass of solute}}}}$

Importance of Some Basic Concepts of Chemistry

This chapter explains the terms related to atomic structure, the periodic table, elements, compounds, and mixtures. They will also recall the physical quantities and their units of measurement. These units will be elaborately used to define other physical quantities and to solve questions related to physical chemistry.

Students will recall what fundamental and derived units are and how their dimensions are recognized. They will proceed to revise and recall the mathematical interpretations and operations of chemical equations used to solve the problems related to physical chemistry.

They will recall what the scientific terms and their definitions are. They will learn the various mathematical operations done to calculate the answers to the fundamental questions in chemistry.

This chapter will also explain the fundamental laws taught such as laws of chemical combination and the conservation of mass in a chemical reaction. It will explain what atomic mass, atomic number, mass number, etc are.

As you can see, this chapter is very important to study and remember the previous concepts and to strengthen your base of knowledge. This base will help you study the vast NEET chemistry syllabus. Refer to Some Basic Concepts of Chemistry Class 11 notes to get more help and add convenience to your study sessions.

Benefits of Some Basic Concepts of Chemistry Class 11 Notes

• These notes are prepared to offer a simpler medium to comprehend and remember the concepts related to Chemistry you studied in the previous years. It will become a lot easier to remember what you have studied and complete preparing this chapter faster.

• Some Basic Concepts of Chemistry notes for NEET will help you to get a simpler version of the definitions, derivations, and mathematical expressions of the formulas. You will become more capable of understanding the basic concepts related to physical chemistry.

• You will also be able to correlate the physical quantities and laws in this chapter and proceed to study the following chapters perfectly. You can use the concise format of these notes to reduce your revision time considerably.

Download Some Basic Concepts of Chemistry Notes PDF

This chapter is of utmost importance as it helps you recall the previous laws, definitions, derivations, and fundamental concepts of chemistry. To make this chapter easier to study and revise, download the Some Basic Concepts of Chemistry NEET notes PDF for free. Make your study sessions more productive using the concise format of these notes.

NEET Chemistry Revision Notes - Chapter Pages

Other Important Links Related to NEET Some Basic Concepts of Chemistry