Class 12 Chemistry Solutions Revision Notes for NEET Preparation
A solution is a type of mixture of two or more components that are mixed homogeneously. In a solution, one of the components remains more in volume than the rest. It is called a solvent and the rest are called solutes. The chapter Solutions describes more concepts related to solutions and solubility. It explains the types of solutions along with their examples. Download and refer to the Solutions Class 12 notes for free from Vedantu.
The subject matter experts have consolidated the concepts and theories related to solutions in this chapter and composed these revision notes. The concise notes will help students preparing for NEET, to learn the definitions, formulas, and descriptions of terms and laws in this chapter.
Note: 👉Get a Head Start on Your Medical Career with the NEET Rank and College Predictor 2025.
NEET Chemistry Revision Notes - Chapter Pages
NEET Chemistry Chapter-wise Revision Notes | |
Classification of Elements and Periodicity in Properties Notes | |
Solutions Notes | |
Access NEET Revision Notes Chemistry Solution
Definition
A solution is a homogeneous mixture of two or more components.
For example the presence of ordinary salt in water.
Classification
Binary solutions are those that have two components. Components are the substances used to create a solution.
The component with the highest concentration is solvent. The solvent determines the physical state of a solution.
A solute is a component of a solution that is present in smaller amounts.
Each element can be solid, liquid, or gaseous.
Types of Solution | Solute | Solvent | Common Examples |
Gaseous Solutions | Gas | Gas | Oxygen and nitrogen gas mixture |
Liquid | Gas | a mixture of chloroform and nitrogen gas | |
Solid | Gas | nitrogen gas with camphor | |
Liquid Solutions | Gas | Liquid | Water with oxygen dissolved in it |
Liquid | Liquid | Ethanol is a liquid that can be dissolved in water. | |
Solid | Liquid | Glucose that has been dissolved in water | |
Solid Solutions | Gas | Solid | Hydrogen solution in palladium |
Liquid | Solid | Mercury and sodium amalgam | |
Solid | Solid | dissolving copper in gold |
Strength of Solutions:
The amount of solute dissolved per unit of solution or solvent is referred to as solution strength. There are several methods for determining a solution's strength.
1. Mass Percentage (%w/w):
“It denotes the mass of a component in 100 g of solution.”
${\rm{Mass \% of \ a \ component}} = \dfrac{{{\rm{ Mass \ of \ component \ in \ the \ sol}}{\rm{. }}}}{{{\rm{ Total \ Mass \ of \ sol}}{\rm{. }}}} \times 100$
2. Volume Percentage (%v/v):
"It represents the volume of a component in a solution of $100{\rm{ mL}}{\rm{.}}$ "
${\rm{Volume \% \ of \ a component}} = \dfrac{{{\rm{ Volume \ of \ component }}}}{{{\rm{ Total \ Volume \ of \ sol}}{\rm{. }}}} \times 100$
3. Mass by Volume Percentage (% w / v):
"It denotes the mass of the solute in grams in $100{\rm{mL of solution}}$ ."
${\rm{Mass \ by \ vol}}{\rm{. percent}} = \dfrac{{{\rm{ Mass \ of \ solute in g}}}}{{{\rm{ Vol}}{\rm{. of \ sol}}{\rm{. in \ mL}}}} \times 100$
4. Parts Per Million (ppm):
Parts per million $ = \dfrac{{{\rm{ No}}{\rm{. of \ parts \ of \ the \ component }}}}{{{\rm{ Total no}}{\rm{. of \ all \ the \ components \ of \ sol}}{\rm{. }}}} \times {10^6}$
Mass to mass, volume to volume, and mass to volume are all ways to express concentration in parts per million.
5. Mole Fraction (x):
"It denotes the number of moles of a solute in one mole of solution."
${\rm{Mole \ fraction}} = \dfrac{{{\rm{ No}}{\rm{. of \ molos \ of \ the \ component }}}}{{{\rm{ Total no}}{\rm{. of \ moles \ all \ the \ components }}}}$
If the amount of moles of A and B in a binary mixture is ${n_{\left\{ {\rm{A}} \right\}}}{\rm{ and }}{n_{\left\{ {\rm{B}} \right\}}},$ respectively, the mole fraction of ${\rm{A}}$ will be
${x_A} = \dfrac{{{n_A}}}{{{n_A} + {n_B}}}$
6. Molarity, M:
"It represents the number of moles of solute in 1 litre of solution."
${\rm{Molarity}},M = \dfrac{{{\rm{ Moles \ of \ solute }}}}{{{\rm{ Vol}}{\rm{. of \ sol \ in \ L}}}}$
Molarity is measured in milligrams per litre and is denoted by the letters ‘${\rm{M}}$ ' or 'Molar.' "The density of a solution is its mass per unit volume."
Density, $d = \dfrac{{{\rm{ Mass \ of \ sol}}{\rm{. }}}}{{{\rm{ Vol}}{\rm{. of \ sol}}{\rm{. }}}} = m/V$
7. Molality, m:
“It denotes the number of moles of solute present per kilogram of solvent.”
${\rm{ Molality, }}m = \dfrac{{{\rm{ Moles \ of \ solute }}}}{{{\rm{ Mass \ of \ solvent in kg}}}}$
Molality is measured in mol/kg, which can also be written as 'm' or 'molal.'
8. Normality, N:
It denotes the number of solute equivalents in 1 litre of solution.
$\begin{array}{l}{\rm{Normality}},N = \dfrac{{{\rm{ No}}{\rm{. of \ Equivalents \ of \ solute }}}}{{{\rm{ Vol}}{\rm{. of \ sol}}{\rm{. in L}}}}\\{\rm{No}}{\rm{. of \ equivalents}},eq = \dfrac{{{\rm{ Weight (}}W{\rm{)}}}}{{{\rm{ Equivalent \ weight (}}E{\rm{)}}}}\\E = \dfrac{M}{z}({\rm{Z \ is \ the \ valency \ factor)}}{\rm{.}}\end{array}$
Some Important Relationships
Dilution Law:
When we dilute a solution with solvent, the solute concentration remains constant, and we can write:
${M_1}{V_1} = {M_2}{V_2}{\rm{ \ and \ }}{N_1}{V_1} = {N_2}{V_2}$
Relation Between Molarity and Normality
${\rm{Normality}} = z \times {\rm{Molarity}}$
Important:
Temperature has no effect on mass percent, ppm, mole fraction, or molality, but it does affect molarity and normality. This is because temperature has no effect on volume but has no effect on mass.
Vapour Pressure
Definition
The vapour pressure of a liquid/solution at a given temperature is the pressure exerted by vapours in equilibrium with the liquid/solution.
${\rm{ Vapour \ pressure }} \propto {\rm{ escaping \ tendency }}$
Vapour Pressure of Liquid Solutions and Raoult’s Law :
(Raoult’s law for volatile solutes)
According to Raoult's law, the partial vapour pressure of each component in a volatile liquid solution is directly proportional to its mole fraction.
${p_1} \propto {x_1}{\rm{ \ and \ }}{p_1} = p_1^0{x_1}$
Component 2 is the same way as follows,
${p_2} = {p_2}^0{x_2}$
According to Dalton's partial pressure law, the total pressure over the solution phase in the container is equal to the sum of the partial pressures of the solution's components and is given as:
${p_{{\rm{(iotal) }}}} = {p_1} + {p_2}$
On substituting the values of ${p_1}$ and ${p_2}$ as follows,
$\begin{array}{c}{p_{({\rm{total }})}} = {x_1}p_1^0{\rm{ and }}{x_2}p_2^0 \\ \\ = \left( {1 - {x_2}} \right)p_1^0 + {x_2}p_2^0 \\ \\ = p_1^0 + \left( {p_2^0 - p_1^0} \right){x_2}\end{array}$
At constant temperature, the plot of vapour pressure and mole fraction of an ideal solution.
Mole Fraction in the Vapour Phase
Using Dalton's law of partial pressures, if ${y_1}$ and ${y_2}$ are the mole fractions of components 1 and 2 in the vapour phase, then:
${p_1} = {y_1}{p_{{\rm{total }}}}$
${p_2} = {y_2}{p_{{\rm{total }}}}$
Generally, the formula can be represented as,
${p_i} = {y_i}{p_{{\rm{total }}}}$
Vapour Pressures of Solutions of Solids in Liquids and Raoult’s Law
(Raoult’s law for non-volatile solutes)
When a nonvolatile solute is added to a solvent to form a solution, the number of solvent molecules leaving the surface decreases, lowering the vapour pressure.
The drop in solvent vapour pressure is determined by the amount of non-volatile solute present in the solution, regardless of its composition.
Raoult's law states, in its most general form, that the partial vapour pressure of each volatile component in a solution is directly proportional to its mole fraction for every solution.
${p_1} \propto {x_1}$
${p_1} = {x_1} p_1^0 = {p_{total{\rm{ }}}}$
If Raoult's law holds true for all concentrations, the vapour pressure of a solution will vary linearly from zero to the vapour pressure of the pure solvent.
Ideal and Non-ideal Solutions
Ideal Solutions:
An ideal solution is one in which each component follows Raoult's rule at all temperatures and concentrations.
Properties of Ideal Solutions:
$\Delta {H_{{\rm{MIXING}}}} = 0$
$\Delta {V_{{\rm{MIXING}}}} = 0$
The attractive forces between A-A and B-B molecules are roughly equivalent to those between A-B molecules.
For example: Benzene and toluene or n-hexane and n-heptane solutions.
Non – ideal Solutions:
A non-ideal solution is one that deviates from Raoult's law over a wide concentration range.
Solutions Showing Positive Deviation From Raoult’s Law:
The forces of solute-solute(B-B) and solvent-solvent(A-A) are weaker than the forces of Solvent-Solute(A-B).
The vapour pressure is higher than predicted by the law.
$\Delta {H_{{\rm{MIXING}}}} > 0$
$\Delta {V_{{\rm{MIXING}}}} > 0$
For example:
Ethanol with acetone or carbon disulphide and acetone.
Negative Deviations From Raoult's law are Shown in the Following Solutions:
The Solvent-Solute (A-B) force is stronger than the other two, and the vapour pressure is lower than predicted by the law.
$\Delta {H_{{\rm{MIXING}}}} < 0$
$\Delta {V_{{\rm{MIXING}}}} < 0$
Examples are phenol and aniline, chloroform and acetone, and so on.
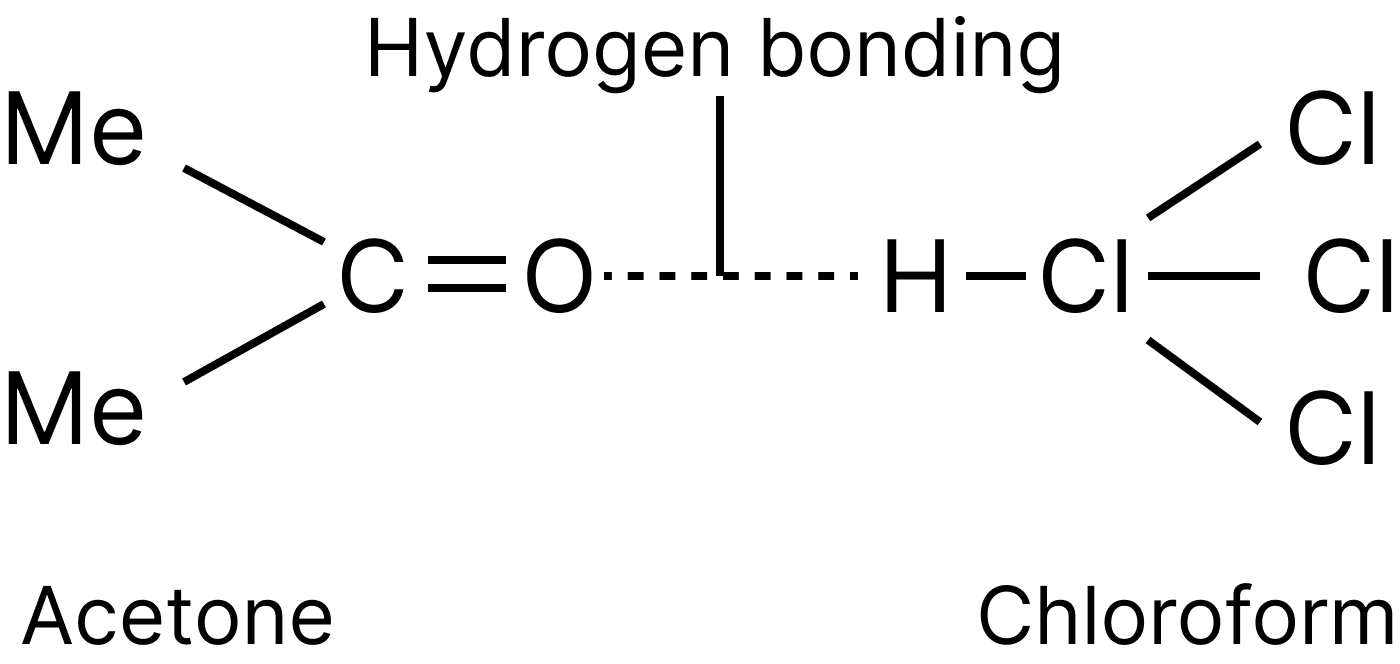
Chloroform and Acetone Deviation
Azeotropes
Azeotropes are binary mixtures that have the same composition in the liquid and vapour phases and boil at the same temperature.
Minimum Boiling Azeotrope
Solutions with a significant positive deviation from Raoult's law form the minimum boiling azeotrope at a given composition.
An azeotrope with a boiling point of 351.15 K, for example, is formed by a mixture of ethanol and water containing approximately 95% ethanol.
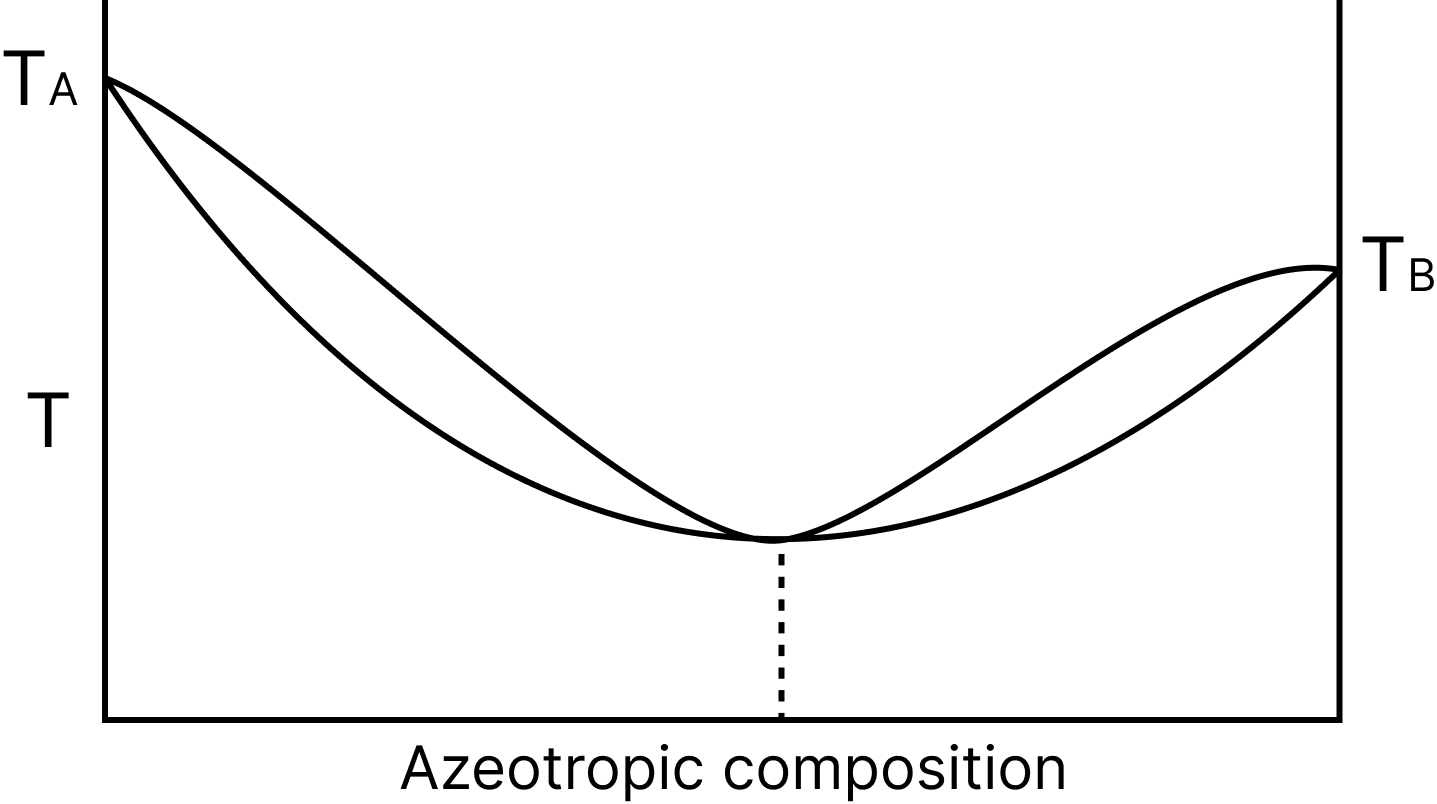
Minimum Boiling Azeotropic Composition
The temperature at which water boils - composition Large positive deviations are depicted in this diagram for solutions (Minimum boiling azeotrope).
Maximum Boiling Azeotrope:
Solutions with a significant negative divergence from Raoult's law form the maximum boiling azeotrope at a given composition. An azeotrope with a boiling point of 393.5 K is produced by a mixture of 68% nitric acid and water.
Maximum Boiling Azeotropic Composition
Water boiling temperature - composition This diagram depicts large negative variances for solutions. (highest boiling point azeotrope)
Solubility
Solubility of a Solid in Liquid
The solubility of a substance refers to how much of it can be dissolved in each amount of solvent.
Factors Impacting a Solid's Solubility in a Liquid Include:
1. Nature of Solute and Solvent:
Like dissolves into like. For example, sodium chloride and sugar dissolve quickly in water, but naphthalene and anthracene do not. Naphthalene and anthracene dissolve rapidly in benzene, but sodium chloride and sugar do not.
2. Temperature:
If $({\Delta _{sol}}H > 0)$ the solubility of a nearly saturated solution increases with the increase in temperature, and if $({\Delta _{{\rm{sol}}}}H < {\rm{0)}}$ the solubility decreases with the increase in temperature.
3. Pressure's Effect:
Because solids and liquids are highly incompressible, this has little impact.
Henry’s law
According to Henry's law, the solubility of a gas in a liquid is directly proportional to the pressure of the gas at a constant temperature.
According to the most common version of Henry's law, "the partial pressure of the gas in the vapour phase (p) is directly related to the mole fraction of the gas (x) in the solution."
The constant ${K_H}$ stands for Henry's law.
Characteristics of ${K_H}$ :
The nature of the gas determines ${K_H}$ .
The lower the solubility of the gas in the liquid, the higher the value of ${K_H}$ at a given pressure.
${K_H}$ values increase as temperature decreases, indicating that gas solubility increases as temperature decreases.
Applications:
In the manufacture of carbonated drinks.
During a deep-water dive.
Climbers and those who live at high altitudes will benefit from this.
Henry's Law as a Specific Example of Raoult's Law
Raoult's law states that
${p_i}{\rm{ }} = {\rm{ }}{x_i}{p_i}^0$
One of the gases in a liquid solution is so volatile that it exists as a gas. It is soluble in water, according to Henry's law.
${p_i}{\rm{ }} = {\rm{ }}{K_H}x$
As a result, Raoult's law becomes a specific case of Henry's law, in which ${K_H}{\rm{ \ equals \ }}{p_i}^0.$
Colligative Properties
Colligative properties are those that are determined by the number of solute particles present in a solution, regardless of their type, in relation to the total number of particles present.
Collaborative qualities include the following:
1. A Relative Decrease in Vapor Pressure
2. Boiling Point Elevation
3. Freezing point depression
4. Osmotic pressure is the factor to consider.
Relative Lowering of Vapour Pressure
The vapour pressure of a solvent decreases when a non-volatile solute is added. The reduction in vapour pressure with respect to the pure solvent's vapour pressure is referred to as "relative lowering in vapour pressure."
Raoult's Law states that:
${p_1}{\rm{ }} = {\rm{ }}{x_1}{p_1}^0$
The reduction in the vapour pressure of solvent $(\Delta {p_1})$ is given as:
$\begin{array}{l}\Delta {p_1} = {p_1}^0 - {p_1}\\ = {p_1}^0 - {p_1}^0{x_1}\end{array}$
$ = {p_1}^0(1 - {x_1})$
It is known that ${x_2} = 1 - {x_1}$ equation then reduces to
$\Delta p = {x_2}{p_1}^0$
This equation can be written as
$\dfrac{{\Delta p}}{{{p_1}^0}} = \dfrac{{{p_1}^0 - {p_1}}}{{{p_1}^0}} = {x_2}$
The expression on the left-hand side of the equation, as previously stated, is known as relative lowering of vapour pressure and equals the mole fraction of the solute. The above equation can be written as:
$\dfrac{{{p_1}^0 - {p_1}}}{{{p_1}^0}}{\rm{ = }}\dfrac{{{n_2}}}{{{n_1} + {n_2}}}\left( {\sin {\rm{ce }}{x_2}{\rm{ = }}\dfrac{{{n_2}}}{{{n_1} + {n_2}}}} \right)$
The number of moles of solvent and solute present in the solution are represented by${n_1}{\rm{ and }}{n_2}$ , respectively. Since ${n_2} < < {\rm{ }}{n_1}$ for dilute solutions, ${n_2}$ in the denominator can be ignored.
$\dfrac{{{p_1}^0 - {p_1}}}{{{p_1}^0}} = \dfrac{{{n_2}}}{{{n_1}}}$
Or
$\dfrac{{{p_1}^0 - {p_1}}}{{{p_1}^0}} = \dfrac{{{w_2} \times {M_1}}}{{{M_2} \times {w_1}}}$
Here,${w_1}{\rm{ and }}{w_2}$ are the masses of the solvent and solute, respectively, while ${M_1}{\rm{ and }}{M_2}$ are the molar masses of the solvent and solute.
Elevation in Boiling Point
The boiling point of a liquid is the temperature at which its vapour pressure equals atmospheric pressure.
When a non-volatile solute is added, the solvent's vapour pressure decreases, requiring a higher temperature to boil the solution. As a result, the solution's boiling point will rise.
Elevation of boiling point is defined as an increase in boiling point $\Delta {T_{\rm{b}}} = {T_{\rm{b}}} - {T_{\rm{b}}}^0,$ where ${T_{\rm{b}}}^0$ is the boiling point of pure solvent and ${T_{\rm{b}}}$ is the boiling point of solution.
Expression:
$\Delta {T_{\rm{b}}} = {K_{\rm{b}}}m$
Boiling Point Elevation Constant, or ${K_{\rm{b}}},$ is also known as the Molal Elevation Constant (Ebullioscopic Constant).
Depression in Freezing Point
The freezing point of a substance is the temperature at which its vapour pressure in its liquid phase equals its vapour pressure in its solid phase.
When a non-volatile solid is introduced into a solvent, the vapour pressure decreases until it equals the vapour pressure of a solid solvent at a lower temperature. As a result, the freezing point of the solvent decreases.
Depression in freezing point is defined $\Delta {T_f} = {T_f}^0 - {T_f},$ where ${T_f}^0$ is the freezing point of pure solvent and ${T_f}$ is the freezing point when a non-volatile solute is dissolved.
Expression
$\Delta {T_f} = {K_f}m$
Freezing Point Depression Constant, Molal Depression Constant, or Cryoscopic Constant are all names for ${K_f}$ .
Osmosis
When a semipermeable membrane separates a pure solvent from a solution, the solvent particles move from the solvent side to the solution side. This phenomenon is known as "osmosis."
Only small molecules can pass through the semi-permeable membrane, while larger solute molecules are blocked.
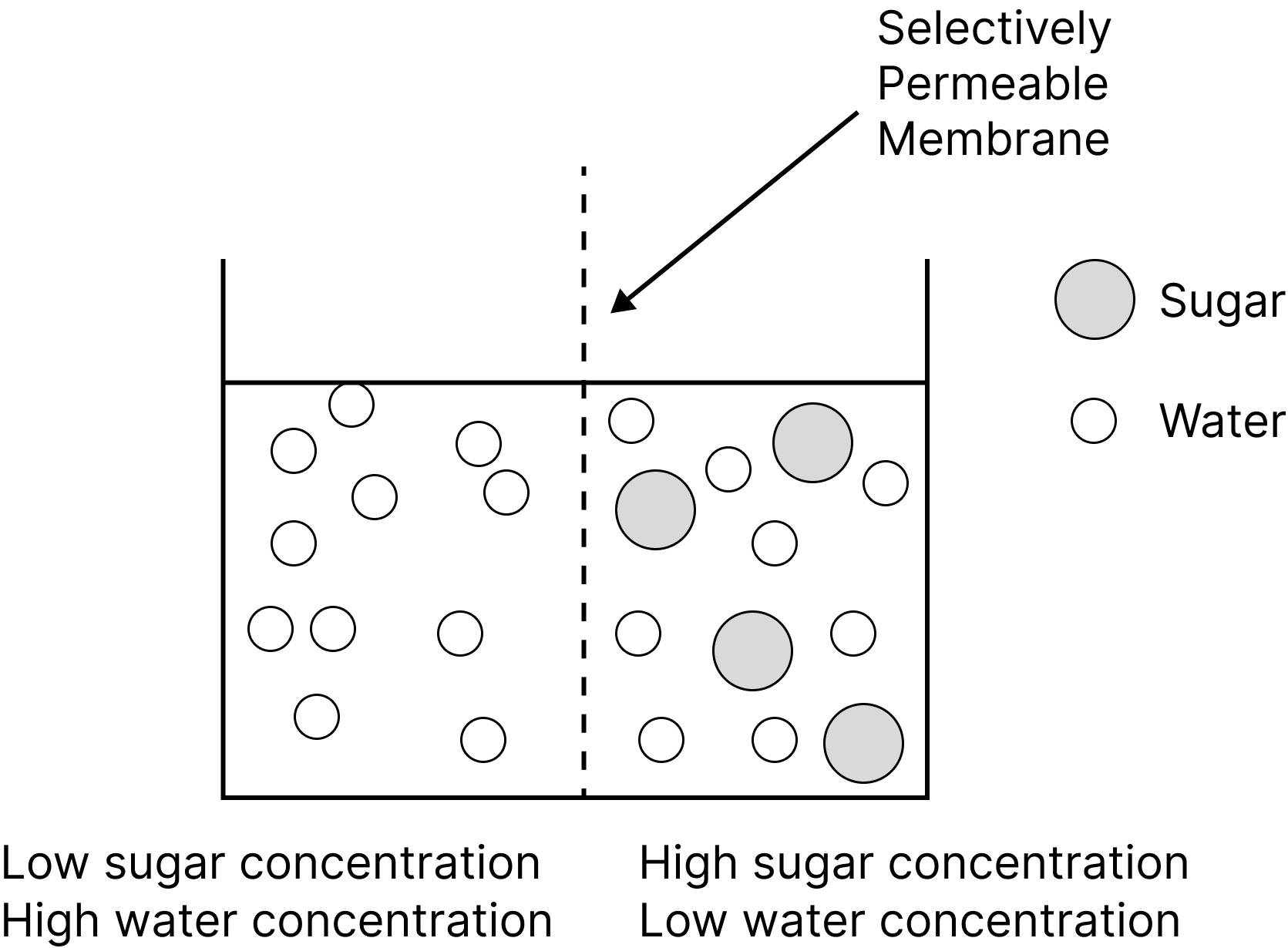
Process of Osmosis
Osmotic Pressure:
The osmotic pressure of a solution is the excess pressure that must be applied to a solution to prevent osmosis, or the flow of solvent molecules through a semipermeable barrier into the solution.
The osmotic pressure must be equal to or greater than the excess pressure. A coating should be applied to the solution to prevent osmosis.
Expression: At a given temperature T, osmotic pressure is directly related to the molarity, C, of a dilute solution.
Thus:
$\pi = C{\rm{ }}R{\rm{ }}T$
Here, osmotic pressure is $\pi $ , while the gas constant is R.
Isotonic Solutions:
Isotonic solutions are defined as two liquids with the same osmotic pressure at the same temperature.
A solution with a lower concentration or lower osmotic pressure than a more concentrated solution is referred to as "Hypotonic."
A solution with a higher concentration or higher osmotic pressure than a dilute solution is referred to as "hypertonic."
Reverse Osmosis:
If a pressure greater than the osmotic pressure is applied to the solution side, the solvent will flow from the solution into the pure solvent through the semipermeable membrane. Reverse osmosis is the name given to this process.
Application:
Desalination of seawater: When a pressure greater than osmotic pressure is applied to the membrane, pure water is squeezed out of the seawater.
Abnormal Molar Masses
When the molecular mass of a substance is determined by investigating any of the colligative qualities and differs from the theoretically expected value, it is said to have aberrant molar mass.
Abnormal Molar Masses are Observed:
1. When a solute in a solution forms a bond.
2. When the solute in the solution dissociates.
Van’t Hoff Factor:
Van't Hoff proposed a factor (i) known as the van't Hoff Factor in order to determine the level of association or dissociation.
$i{\rm{ = }}\dfrac{{{\rm{Normal \ molar \ mass}}}}{{{\rm{Abnormal \ molar \ mass}}}}$
$\begin{array}{l}i{\rm{ = }}\dfrac{{{\rm{Observed \ colligative \ property}}}}{{{\rm{Calculated \ colligative \ property}}}} \\ \\ = \dfrac{{{\rm{Total \ no}}{\rm{. of \ moles \ of \ particles \ after \ association(dissociation)}}}}{{{\rm{No}}{\rm{. of \ moles \ of \ particles \ before \ association(dissociation)}}}}\end{array}$
Modified Expressions:
Relatively lowering of solvent’s vapour pressure as shown below.
$\dfrac{{{p_1}^0 - {p_1}}}{{{p_1}^0}} = i.\dfrac{{{n_2}}}{{{n_1}}}$
Depression of Freezing point:
$\Delta {T_f} = i{K_f}m$
Osmotic pressure of solution:
$\pi = {\rm{ }}i{\rm{ }}{n_2}{\rm{ }}RT/V$
Vapour Pressure
When the temperature of a liquid rises, so does the desire of the molecules to escape, and the vapour pressure rises. The distribution of kinetic energy among molecules in a liquid.
Clausius-Clapeyron Equation
The equation can be represented as:
${p_2}/{p_1} = (\Delta {H_{{\rm{VAP}}}}/R)(1/{T_1} - 1/{T_2})$
Here, $\Delta {H_{{\rm{VAP}}}}$ represents the liquid's vaporisation enthalpy.
Examples:
1. 4 litres of $0.02{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{M}}$ aqueous solution of ${\rm{NaCl}}$ was diluted by adding one litre of water. The molality of the resultant solution is _____________.
(A) $0.004$
(B) $0.008$
(C) $0.012$
(D) $0.016$
Correct Answer: Option (D)
Explanation:
Volume ${V_1} = 4{\kern 1pt} {\kern 1pt} L$
Molarity ${M_1} = 0.02{\kern 1pt} {\kern 1pt} {\rm{M}}$
Volume ${V_2} = 4 + 1 = 5{\rm{L}}$
The formula used will be:
${M_1}{V_1} = {M_2}{V_2}$
By substituting the values in the formula ${M_1}{V_1} = {M_2}{V_2}$ we get
$\begin{array}{l}{M_1}{V_1} = {M_2}{V_2}\\0.02 \times 4 = {M_2} \times 5\end{array}$
$\begin{array}{l} \Rightarrow {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {M_2} = \dfrac{{0.02 \times 4}}{5}\\ \Rightarrow {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {M_2} = 0.016{\kern 1pt} {\kern 1pt} {\rm{M}}\end{array}$
Thus, the molarity of the resultant solution is $0.016{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{M}}$.
2. Relative lowering of vapour pressure is a colligative property because _____________.
(A) It depends on the concentration of a non electrolyte solute in solution and does not depend on the nature of the solute molecules.
(B) It depends on number of particles of electrolyte solute in solution and does not depend on the nature of the solute particles.
(C) It depends on the concentration of a non electrolyte solute in solution as well as on the nature of the solute molecules.
(D) It depends on the concentration of an electrolyte or nonelectrolyte solute in solution as well as on the nature of solute molecules.
Correct Answer: Option (i) and option (ii)
Explanation:
The relative lowering of vapour pressure depends on the concentration of a nonelectrolyte solute in a solution and the number of particles of electrolyte solute in a solution. The relative lowering of vapour pressure does not depend on the nature of the solute molecules and the nature of the solute particles. That is why it is a colligative property.
3. Which of the following binary mixtures will have the same composition in liquid and vapour phase?
(A) Benzene - Toluene
(B) Water - Nitric acid
(C) Water - Ethanol
(D) n-Hexane - n-Heptane
Correct Answer: Option (ii) and option (iii)
Explanation:
The mixture having the same composition in liquid as well as the vapour phase is known as azeotropes. The property of azeotropic mixture is that it boils are the same temperature.
The solutions, water-nitric acid and water-ethanol are non-ideal solutions which have the same composition in liquid and vapour phase, hence they are azeotropes. While benzene-toluene and n-hexane-n-heptane are ideal solutions so they will not behave as azeotropes.
Importance of Solutions in Class 12 Chemistry
This chapter discusses the terms related to solutions and solubility. It is a part of the physical chemistry syllabus students study while preparing for NEET. This chapter explains the different types of solutions and their examples.
It covers what vapour pressure is and how it is explained by Raoult’s Law. The law is discussed using proper scientific terms and mathematical expressions so that students can use the concept of vapour pressure to solve numerical problems.
This law can be made a complementary part of Dalton’s Law of partial pressure expressing the fact the vapour of a solution is subjected to behave like gases and follows these laws.
The chapter covers what ideal and non-ideal solutions are along with their mathematical derivations. It describes colligative properties of solutions. The different factors regarding vapour pressure and boiling point of solvents are also explained in this chapter. It also explains how the freezing point of a non-volatile solid can be depressed.
On proceeding further, it covers what osmotic pressure and osmosis are. In this context, it discusses different types of solutions related to the densities of solute and osmotic pressure.
We can clearly understand how important this chapter is to understand the scientific terms and derivations of formulas of solutions. The Solutions NEET notes will help you to learn and revise all these topics and sub-topics quickly before the exam.
Benefits of Solutions Class 12 Notes NEET
These NEET revision notes have been designed to offer a simpler version of the entire chapter. Students will find revising the key topics of this chapter using these notes much easier than referring to the textbook.
The prime objective of our subject experts for preparing Solutions Class 12 notes NEET is to segregate the important topics and concepts and make them easier to comprehend and memorize. Hence, memorizing the definitions and formulas of this chapter will become a lot easier.
Students get highly benefitted from these notes when they can reduce their revision sessions to a considerable extent. They can use their precious time to prepare and complete the syllabus of Chemistry for NEET by using these notes.
Study the sample questions given in the Solution Chemistry Class 12 notes and find out how the experts have answered them.
Download Free Chemistry Solutions NEET Notes PDF
With the help of these revision notes cover the chapter of Solutions effectively for the NEET exam. You can refer to these notes to resolve doubts on your own. These Solutions Class 12 notes NEET PDF is free for download and ideal for revising the formulas and definitions of this chapter and solving problems accurately.
Other Important Links Related to NEET Solutions
Other Important Links for NEET Solutions |
FAQs on Solutions Class 12 Notes NEET Chemistry (Free PDF Download)
1. Where does a solute go when mixed in a solvent?
When a solute is mixed in a solvent, the volume of the solvent remains the same. It means that the solute particles take the intermolecular spaces between the solvent particles.
2. What is vapour pressure?
The pressure of a vapour remaining in contact with it liquid or solid form is called vapour pressure.
3. Give an example of a gas-solid solution.
Palladium absorbs hydrogen to form a gas-solid solution.
4. What is smoke?
Smoke is a solid-gas solution of soot and air.



















