Electrochemistry Class 12 Notes for NEET Chemistry Revision

Electrochemistry

Electrochemistry is the study of producing electricity from chemical reactions that occur spontaneously as well as the use of electrical energy to cause chemical reactions that don't occur spontaneously.

Electrochemical Cells

• The Gibbs energy of the system falls as the possibility of a spontaneous chemical reaction increases.

• The energy is then changed into electrical energy. External energy can also be utilised to compel the occurrence of non-spontaneous processes in the form of electrical energy. 

• These interconversions are carried out using electrochemical cells.

There are Two Types of Electrochemical Cells:

• Galvanic and

• Electrolytic cells 

Galvanic cells convert chemical energy into electrical energy, whereas electrolytic cells turn electrical energy into chemical energy.

Galvanic Cells

• To extract cell energy, a spontaneous chemical process or reaction is performed, which is subsequently converted to electric current.

• A Daniel Cell, for example, is a Galvanic Cell that performs the redox process utilising Zinc and Copper.

$Zn(s) + C{u^{2 + }}(aq) \to Z{n^{2 + }}(aq) + Cu(s)$ 

Oxidation Half: $Zn(s) \to Z{n^{2 + }}(aq) + 2{e^ - }$ 

Reduction Half: $C{u^{2 + }}(aq) + 2{e^ - } \to Cu(s)$ 

$Zn$ is the reducing agent, while $C{u^{2 + }}$ is the oxidising agent. 

• Half cells are also known as electrodes. The oxidation half is the anode, while the reduction half is the cathode. 

• A form of electrode is referred to as a cathode. Electrons travel from the anode to the cathode in the external circuit. 

• The anode is given negative polarity. The cathode is given positive polarity. Daniell Cell is a fictional character that Daniell Cell has developed. The anode is $Zn$, and the cathode is $Cu$. 

Electrolytic Cell

• These electrodes are immersed in a solution containing both cations and anions. 

• When current is applied, the ions travel to electrodes of opposite polarity, where they are reduced and oxidized simultaneously.

Preferential Discharge of Ions

• The discharge process becomes competitive when more than one cation or anion is present. 

• Any ion that needs to be discharged requires energy, and if there are several ions present, the one that requires the most energy discharges first.

Electrolysis 

• When an electric current is carried through an electrolyte's aqueous solution or in the fused state, the electrolyte decomposes.

• Cations gain electrons and convert into neutral atoms as they approach the cathode. Anions, meanwhile, go to the anode, where they lose electrons and become neutral atoms. 

• Metal electrorefining uses impure metals as the anode and a strip of pure metal as the cathode.

Faraday’s Laws of Electrolysis 

Faraday proposed the following two laws to explain the relationship between the amount of substance produced and the current or equivalent weight.

1. First Law of Electrolysis 

It states that "the amount (mass) of any substance deposited or liberated at any electrode is directly proportional to the amount of electricity passed through the electrolyte."

$\begin{array}{c}w \propto Q\\w = ZQ\\ = Zit\\{\rm{Charge}}\left( Q \right) = {\rm{current}}\left( i \right) \times time\left( t \right)\end{array}$

Z = Electrochemical equivalence

$Z = \dfrac{E}{{96500}}$ 

(where, E = Equivalent weight) 

2. Second Law of Electrolysis 

"When the same amount of electricity is passed through solutions of different electrolytes connected in series, the weight of substance produced at the electrodes is directly proportional to their equivalent weight," it states. 

i.e. $\dfrac{\text { Weight of } \mathrm{Cu} \text { deposited }\left(w_{1}\right)}{\text { Weight of Ag deposited }\left(w_{2}\right)}=\dfrac{\text { Equivalent weight of } \mathrm{Cu}\left(E_{1}\right)}{\text { Equivalent weight of } \mathrm{Ag}\left(E_{2}\right)}$

Electrode Potential

• When an element comes into contact with its ions, it tends to lose or gain electrons, leading it to become positively or negatively charged. 

• The electrode potential is referred to as oxidation or reduction potential depending on whether oxidation or reduction has happened.

$M(s)\underset{{{\text{Reduction}}}}{\overset{{{\text{Oxidation}}}}{\longleftrightarrow}}{M^{n + }}(aq) + n{e^ - }$ 

${M^{n + }}(aq) + n{e^ - }\underset{{{\text{Oxidation}}}}{\overset{{{\text{Reduction}}}}{\longleftrightarrow}}M(s)$ 

Characteristics

• The oxidation and reduction potentials have the same magnitude and sign.

• The values of E do not add up since it is not a thermodynamic property.

Standard Electrode Potential $({E^ \circ })$ 

It's defined as the electrode potential of a given electrode when compared to a standard hydrogen electrode under standard conditions. The standard conditions are as follows:

• Each ion in the solution has a concentration of 1 M.

• A temperature of 298 K.

• Each gas has a one-bar pressure.

Electrochemical Series

The half-cell potential values are standard, and they are represented as standard reduction potential values in the Electrochemical Series table at the end.

Cell Potential or EMF of a Cell

The difference between the electrode potential of two half cells is called cell potential. Electromotive force occurs when no current is drawn from the cell (EMF).

${E_{cell}} = {E_{cathode}} + {E_{anode}}$ 

We use the anode's oxidation potential and the cathode's reduction potential in this equation.

Since the anode is on the left and the cathode is on the right, the following is the result:

$ = {E_R} + {E_L}$ 

For a Daniel Cell, therefore:

$E_{cell}^ \circ  = E_{C{u^{2 + }}/Cu}^ \circ  - E_{Zn/Z{n^{2 + }}}^ \circ  = 0.34 + (0.76) = 1.10V$ 

Cell Diagram or Representation of a Cell

The following conventions or notations are used to write the cell diagram by IUPAC regulations. 

The Daniel cell is represented as follows:

$Zn(s)|Z{n^{2 + }}({C_1})||C{u^{2 + }}({C_2})|Cu(s)$ 

• The anode half cell is written on the left, while the cathode half cell is written on the right. 

• The metal is separated from an aqueous solution of its own ions by a single vertical line.

Anodic Chamber: $Zn(s)|Z{n^{2 + }}(aq)$ 

Cathodic Chamber: $C{u^{2 + }}(aq)|Cu(s)$ 

• A double vertical line represents a salt bridge.

• The molar concentration (C) is provided in brackets after the formula of the relevant ion.

• The e.m.f value of a cell is inscribed on the cell's far right side. Consider the following scenario:

$Zn(s)|Z{n^{2 + }}(1M)||C{u^{2 + }}(1M)|Cu$ , EMF = +1.1 V

• The working electrode may be noted adjacent to any inert electrodes that were used to construct the cell, such as platinum, when a zinc anode is connected to a hydrogen electrode, for instance.

$Zn(s)|Z{n^{2 + }}({C_1})||{H^ + }({C_2})|{H_2}(Pt)(s)$ 

Salt Bridge

The salt bridge keeps the balance of charges and completes the circuit by allowing ions to pass freely over it.

It has a gel inside with an inert electrolyte like $N{a_2}S{O_4}$ or $KN{O_3}$ as an electrolyte. Negative ions migrate to the anode and positive ions move across the salt bridge to the cathode, maintaining the equilibrium of charges in the cell.

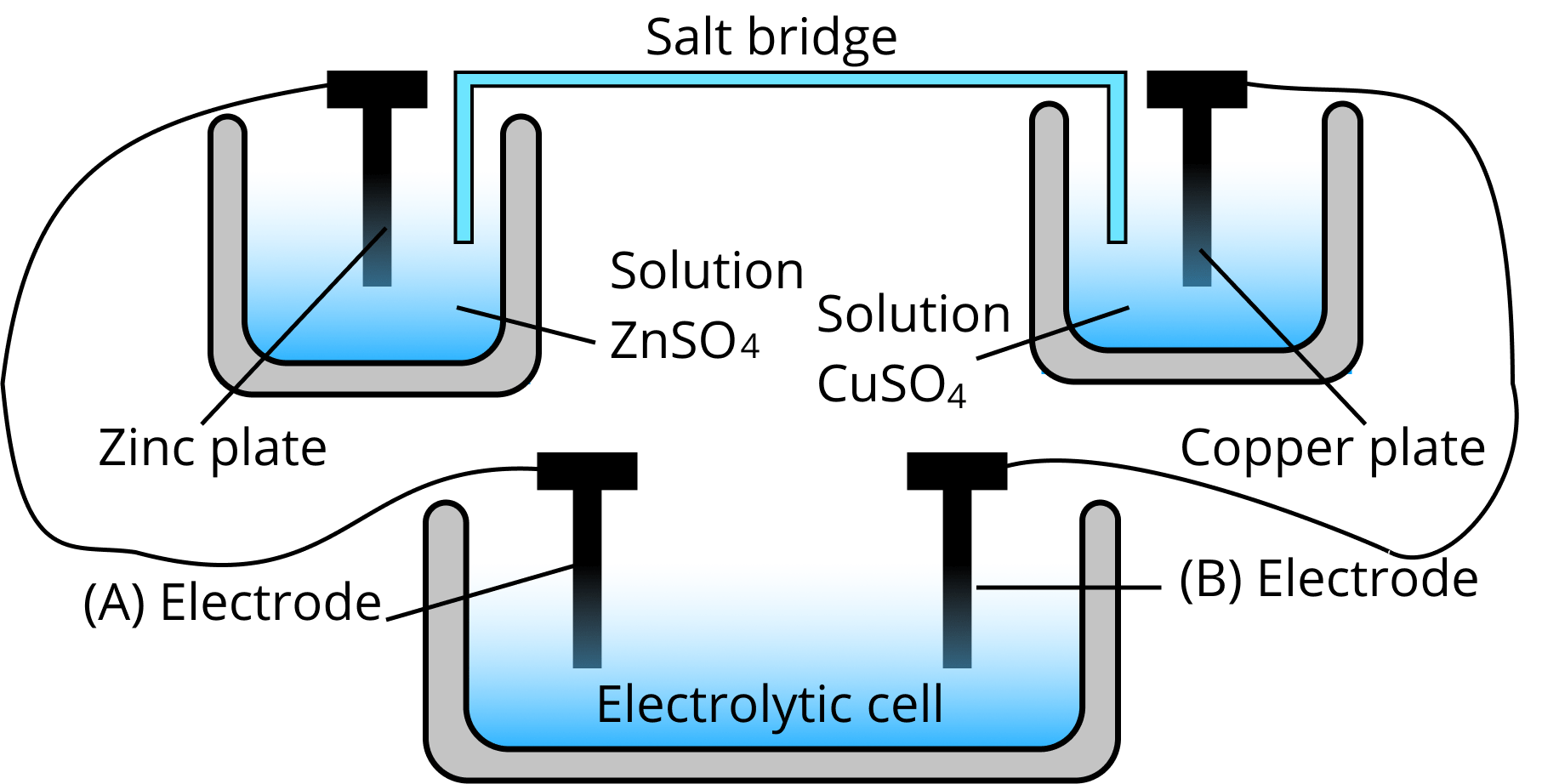
Diagram of Salt Bridge

Spontaneity of a Reaction

$\Delta G =  - nF{E_{cell}}$ 

$\Delta G$ must be negative and cell potential must be positive for a spontaneous cell response to occur.

The standard value of $\Delta G$ will be obtained if we utilise the standard value of cell potential in the following equation.

$\Delta {G^ \circ } =  - nFE_{cell}^ \circ $ 

Types of Electrodes

Metal – Metal Ion electrodes

• Metal ions are present in an electrolyte solution that is submerged beneath a metal rod or plate.

• Due to the voltage differential between these two phases, this electrode has the ability to function as both a cathode and an anode.

At anode: $M \to {M^{n + }} + n{e^ - }$ 

At cathode: ${M^{n + }} + n{e^ - } \to M$ 

Gas Electrodes

• In conjunction with their respective ions, electrode gases like${H_2}$ and $C{l_2}$ are utilized. For instance, a diluted solution of $HCl$ (${H^ + }$ ions is used in conjunction with H2 gas.

• The metal must be inert to avoid interacting with the acid.

• The potentials of other electrodes are also measured using the hydrogen electrode as a reference. Its potential is set to $0V$ for reference.

• The electrode is referred to as the "Standard Hydrogen Electrode (SHE)" and the concentration of the HCl used as a reference is 1 M.

Metal – Insoluble Salt Electrode

We employ a variety of salts that are only very little soluble in the metal itself as electrodes.

For instance, when using $AgCl$ with $Ag$ , there may be a gap between these two phases, as demonstrated by the following reaction:

$AgCl(s) + {e^ - } \to Ag(s) + C{l^ - }$

A silver rod is submerged in a solution comprising $AgCl(s)$ and $C{l^ - }$ ions to create this electrode.

Calomel Electrode

Calomel paste $(H{g_2}C{l_2})$ and an electrolyte that contains $C{l^ - }$  ions) are mixed with mercury.

At cathode: $H{g_2}C{l_2}(s) + 2{e^ - } \to 2Hg(l) + 2C{l^ - }(aq)$ 

At anode: $2Hg(l) + 2C{l^ - }(aq) \to H{g_2}C{l_2}(s) + 2{e^ - }$ 

This electrode is also used to establish other potentials as a reference point. In its standard form, it is also known as Standard Calomel Electrode (SCE).

Redox Electrode

In these electrodes, the same metal is employed in two different oxidation states in the same half cell. For instance, when $F{e^{2 + }}$ and $F{e^{3 + }}$ are dissolved in the same container and an inert platinum electrode is used to transfer electrons.

Possible reactions include the following:

At anode: $F{e^{2 + }} \to F{e^{3 + }} + {e^ - }$ 

At cathode: $F{e^{3 + }} + {e^ - } \to F{e^{2 + }}$ 

Nernst Equation

The relationship between electrode voltage and ion concentration is established. As a result, the reduction potential increases together with the increase in ion concentration. for a common electrochemical reaction type.

$aA + bB\xrightarrow{{n{e^ - }}}cC + dD$ 

The Nernst equation can be written as:

${E_{{\text{cell}}}} = E_{{\text{call}}}^0 - \dfrac{{RT}}{{nF}}\ln \dfrac{{{{[C]}^c}{{[D]}^d}}}{{{{[A]}^a}{{[B]}^b}}}$

${E_{c \in l}} = E_{cdl}^ \circ  - \dfrac{{2303}}{{nF}}RT\log \dfrac{{{{[C]}^c}{{[D]}^d}}}{{{{[A]}^a}{{[B]}^b}}}$

Here, substitute the values of R and F as follows:

${E_{{\text{cell}}}} = E_{ccll}^0 - \dfrac{{0.0591}}{n}\log \dfrac{{{{[C]}^c}{{[D]}^d}}}{{{{[A]}^a}{{[B]}^b}}}$

Applications of Nernst Equation

Equilibrium Constant from Nernst Equation

For a Daniel Cell, at equilibrium

${{E_{{\text{cell}}}} = 0 = E_{{\text{cell}}}^0 - \dfrac{{2.303{\text{RT}}}}{{2{\text{F}}}}\log \dfrac{{\left[ {{\text{Z}}{{\text{n}}^{2 + }}} \right]}}{{\left[ {{\text{C}}{{\text{u}}^{2 + }}} \right]}}}$

${{\text{E}}_{{\text{cdl}}}^{\text{o}} = \dfrac{{2.303{\text{RT}}}}{{2{\text{F}}}}\log \dfrac{{\left[ {{\text{Z}}{{\text{n}}^{2 + }}} \right]}}{{\left[ {{\text{C}}{{\text{u}}^{2 + }}} \right]}}}$ 

But at equilibrium:

$\dfrac{{\left[ {Z{n^{2 + }}} \right]}}{{\left[ {C{u^{2 + }}} \right]}} = {K_c}$

${{\text{E}}_{cell}^{\text{a}} = \dfrac{{2.303{\text{RT}}}}{{2{\text{F}}}}\log {{\text{K}}_{\text{c}}}}$

${{\text{E}}_{cell}^{\text{o}} = \dfrac{{2.303 \times 8.314 \times 298}}{{2 \times 96500}}\log {{\text{K}}_{\text{c}}}}$

${ = \dfrac{{0.0591}}{2}\log {{\text{K}}_{\text{c}}}}$ 

In general:

${{\text{E}}_{{\text{cell}}}^ \circ  = \dfrac{{0.0591}}{{\text{n}}}\log {{\text{K}}_{\text{c}}}}$ 

${\log {{\text{K}}_{\text{c}}} = \dfrac{{{\text{n}}E_{{\text{cell}}}^ \circ }}{{0.0591}}}$

Concentration Cells

When two electrodes of the same metal are individually dipped into two solutions of the same electrolyte with variable concentrations, and the solutions are connected by a salt bridge, concentration cells are created. For illustration:

${H_2}|{H^ + }({C_1})||{H^ + }({C_2})|{H_2}$ 

$Cu|C{u^{ + 2}}({C_1})||C{u^{2 + }}({C_2})|Cu$

These are of two types:

1. Electrode Concentration Cells

${H_2}({P_1})|{H^ + }(C)||{H^ + }(C)|{H_2}({P_2})$ 

${E_{{\text{cell}}}} = 0 - \dfrac{{0.059}}{n}\log \dfrac{{{P_2}}}{{{P_1}}}$

Where, ${P_2} < {P_1}$ for spontaneous reaction.

2. Electrolyte Concentration Cell

At 298 K, the EMF of concentration cell can be written as

$Zn|Z{n^{2 + }}({C_1})||Z{n^{2 + }}({C_2})|Zn$ 

${{\text{E}}_{{\text{cell}}}} = \dfrac{{0.0591}}{{{{\text{n}}_1}}}\log \dfrac{{{{\text{c}}_2}}}{{{{\text{c}}_{\text{l}}}}}$

Where, ${C_2} > {C_1}$ for spontaneous reaction

Cases of Electrolysis

1. Electrolysis of Molten Sodium Chloride

$2NaCl(l) \rightleftharpoons 2N{a^ + }(l) + 2C{l^ - }(l)$ 

The reactions is taking place at the two electrodes may be shown as follows:

At cathode: $2N{a^ + } + 2{e^ - } \to 2Na$ , ${E^ \circ } =  - 2.71V$ 

At anode: $2C{l^ - } \to C{l_2} + 2{e^ - }$ , ${E^ \circ } =  - 1.36V$ 

Overall reaction:

$2N{a^ + }(l) + 2C{l^ - }\xrightarrow{{electrolysis}}2Na(l) + C{l_2}(g)$ OR

$2NaCl(l)\xrightarrow{{electrolysis}}2Na(l) + C{l_2}(g)$ 

Electrolysis of an aqueous solution of Sodium Chloride

$NaCl(aq) \to N{a^ + }(aq) + C{l^ - }(aq)$ 

${H_2}O(l) \rightleftharpoons {H^ + }(aq) + O{H^ - }(aq)$ 

At cathode:

$2N{a^ + } + 2{e^ - } \to 2Na$ , ${E^ \circ } =  - 2.71V$ 

$2{H_2}O + 2{e^ - } \to {H_2} + 2O{H^ - }$ , ${E^ \circ } =  - 0.83V$ 

Thus ${H_2}$  gas is generated at cathode value $N{a^ + }$  ions and remains in solution.

At anode:

$2{H_2}O \to {O_2} + 4{H^ + } + 4{e^ - }$ , ${E^ \circ } =  - 1.23V$ 

$2C{l^ - } \to C{l_2} + 2{e^ - }$ , ${E^ \circ } =  - 1.36V$ 

As a result, the over-voltage principle is used at the anode to evolve $C{l_2}$ gas while leaving $O{H^ - }$ ions in the solution.

Batteries

When Galvanic cells are joined in series to produce a larger voltage, the arrangement is referred to as a "battery."

Primary Batteries

As long as active components are available, primary cells can be used indefinitely. The cell stops functioning and cannot be utilised once they are gone. A Dry Cell, a Leclanche Cell, a Mercury Cell, for instance.

Dry Cell

• Anode: Zinc container

• Cathode: Carbon (graphite) rod surrounded by powdered $Mn{O_2}$ and carbon

• Electrolyte: $N{H_4}Cl$ and $ZnC{l_2}$ 

• Reaction:

• Anode: $Zn \to Z{n^{2 + }} + 2{e^ - }$ 

• Cathode: $Mn{O_1} + NH_{_4}^ +  + {e^ - } \to MnO(OH) + N{H_3}$ 

This cell's typical potential is 1.5 V, and it cannot be replaced once it has been used. This potential diminishes when the battery is continuously depleted.

Mercury Cells

These are utilised in hearing aids and other small pieces of equipment.

• Anode: $Zn - Hg$ Amalgam

• Cathode: Paste of $HgO$ and carbon

• Electrolyte: Paste of $KOH$ and $ZnO$ 

• Anode: $Zn(Hg) + 2O{H^ - } \to ZnO(s) + {H_2}O + 2{e^ - }$ 

• Cathode: $HgO(s) + {H_2}O + 2{e^ - } \to Hg(l) + 2O{H^ - }$ 

• Overall Reaction: $Zn(Hg) + HgO(s) \to ZnO(s) + Hg(l)$ 

The cell potential is roughly 1.35 V and remains constant throughout the life of the cell.

Secondary Batteries

There are numerous applications for secondary batteries that allow for multiple recharges. For instance, lead storage batteries and $Ni - Cd$ batteries.

Lead Storage Battery

• Anode: Lead $(Pb)$ 

• Cathode: Grid of lead packed with lead oxide $(Pb{O_2})$ 

• Electrolyte: 38% solution of ${H_2}S{O_4}$ 

• Discharging Reaction

• Anode: $Pb(s) + SO_4^{2 - }(aq) \to PbS{O_4}(s) + 2{e^ - }$ 

• Cathode: $Pb{O_2}(s) + 4{H^ + }(aq) + SO_4^{2 - }(aq) + 2{e^ - } \to PbS{O_4}(s) + 2{H_2}O(l)$ 

• Overall Reaction: $Pb(s) + Pb{O_2}(s) + 2{H_2}S{O_4}(aq) \to 2PbS{O_4}(s) + 2{H_2}O(l)$ 

The cell is connected to a cell with a greater potential, which functions as an electrolytic cell and reverses the processes, to recharge it. $Pb(s)$ and $Pb{O_2}(s)$ are regenerated at the pertinent electrodes. The voltage generated by these cells is almost constant.

• Recharging Reaction: $2PbS{O_4}(s) + 2{H_2}O(l) \to Pb(s) + Pb{O_2}(s) + 2{H_2}S{O_4}(aq)$ 

Fuel Cells

• The reactants in a fuel cell are supplied externally from a reservoir as opposed to being stored inside the cell, which is how it differs from a conventional battery.

• Fuel cells are used in space vehicles, and the two gases are supplied from outside storage. This cell's electrolyte is KOH, and the electrodes are carbon rods.

• Cathode: ${O_2}(g) + 2{H_2}O(l) + 4{e^ - } \to 4O{H^ - }(aq)$ 

• Anode: $2{H_2}(g) + 4O{H^ - }(aq) \to 4{H_2}O(l) + 4{e^ - }$ 

• Overall Reaction: $2{H_2}(g) + {O_2}(g) \to 2{H_2}O(l)$ 

Corrosion

• It involves a redox process and the growth of an electrochemical cell on the surface of iron or any other metal.

• At one location, oxygen is reduced to produce water, whereas at another, iron is oxidised (anode) (cathode)Rust, which is symbolised as  $F{e 2}{O 3}. x{H 2}O$, is created by first oxidising iron to form $F{e^{2 + }}$, which is then transformed into $F{e^{3 + }}$ in the presence of oxygen which reacts with water.

• Anodic reaction: $2Fe(s) \to 2F{e^{2 + }} + 4{e^ - }$ , ${E^ \circ } =  + 0.44V$ 

• Cathodic reaction: ${O_2}(g) + 4{H^ + } + 4{e^ - } \to 2{H_2}O(l)$ , ${E^ \circ } = 1.23V$ 

• Overall Reaction: $2Fe(s) + {O_2}(g) + 4{H^ + } \to 2F{e^{2 + }} + 2{H_2}O$ , $E_{Cell}^ \circ  = 1.67M$ 

• Iron can be protected from rusting by painting it or covering it with another metal, such as zinc. The latter process is known as galvanization.

• Iron is shielded while Zn is oxidised first because Zn has a higher propensity for oxidation than iron. This method of separating one metal from the other is known as cathodic protection.

Conductance (G)

It is the inverse of resistance and is described as the ease with which electric current flows through a wire.

$G = \dfrac{1}{R}$ 

SI unit is Siemen (S).

$1S = 1oh{m^{ - 1}}(mho)$ 

Conductivity 

It is the reciprocal of resistivity $(\rho )$ .

$\kappa  = \dfrac{1}{\rho } = \dfrac{1}{R} \times \dfrac{\ell }{A} = G \times \dfrac{\ell }{A}$

Now is $l = 1cm$ and $A = 1c{m^2}$ , then $\kappa  = G$ 

As a result, the conductance of a solution with a cross-sectional area of $1c{m^2}$ and a length of $1cm$ can be used to describe an electrolytic solution's conductivity.

Factors Affecting Electrolytic Conductance

Electrolyte

An electrolyte is a substance that conducts electricity when it dissociates into ions in solution when it is dissolved or molten.

Examples of strong electrolytes include $HCl,NaOH,KCl$, while weak electrolytes include $C{H_3}COOH,N{H_4}OH$

The conductance of electricity by ions present in solutions is referred to as electrolytic or ionic conductance. The electricity that passes through an electrolyte solution is controlled by the following variables.

• Electrolyte nature or interionic attractions: The flexibility of ion mobility is greater and conductance is higher the less solute-solute interactions there are.

• Ion Solvation: As the number of interactions between the solute and the solvent rises, so does the degree of solvation, and the electrical conductance falls.

• The nature of the solvent and its viscosity: The solvent's resistance to ion flow, and the electrical conductance all increase as the solvent-solvent interactions increase.

• Temperature: Reduced interactions between solute and solute, solute and solvent, and solvent and solvent when the temperature of an electrolytic solution rises lead to an increase in electrolytic conductance.

Measurement of Conductance

It is known that, $\kappa  = \dfrac{1}{{\text{R}}} \times \dfrac{\ell }{{\text{A}}}$

We can determine the value of $\kappa $ by measuring $l$, $A$, and $R$. The resistance of the solution $R$ between two parallel electrodes is computed using the "Wheatstone" bridge method.

It consists of a conductivity cell with an unknown resistance ${R 2}$, a conductivity cell with two fixed resistances ${R 3}$ and ${R 4}$, and a variable resistance ${R 1}$. The bridge is balanced when there is no current flowing through the detector. Then, under these conditions:

$\dfrac{{{R_1}}}{{{R_2}}} = \dfrac{{{R_3}}}{{{R_4}}}$  or ${R_2} = \dfrac{{{R_1}{R_4}}}{{{R_3}}}$ 

Molar Conductivity

It is the combined conductivity of all the ions produced when one mole of an electrolyte is dissolved between two large electrodes spaced one centimetre apart.

Mathematically, it can be expressed as,

${{\text{}{\Lambda }}_{\text{m}}} = \kappa  \times {\text{V}},\quad {{\text{}{\Lambda }}_{\text{m}}} = \dfrac{{\kappa  \times 1000}}{{\text{C}}}$

 where, V is the volume of solution in $c{m^3}$  containing 1 mole of electrolyte and C is the molar concentration.

Units: ${{{\text{}{\Lambda }}_{\text{m}}} = \dfrac{{\kappa  \times 1000}}{{\text{C}}} = \dfrac{{{\text{Sc}}{{\text{m}}^{ - 1}}}}{{{\text{molc}}{{\text{m}}^{ - 3}}}}}$

${ = {\text{oh}}{{\text{m}}^{ - 1}}{\text{c}}{{\text{m}}^2}{\text{mo}}{{\text{l}}^{ - 1}}{\text{or Sc}}{{\text{m}}^2}{\text{mo}}{{\text{l}}^{ - 1}}}$ 

Equivalent Conductivity

It measures the electrical conductivity of a comparable electrolyte sandwiched between two substantial electrodes spaced a centimetre apart.

Mathematically, it can be written as,

${{{\text{}{\Lambda }}_{{\text{eq}}}} = \kappa  \times {\text{v}} = }$

${{{\text{}{\Lambda }}_{{\text{eq}}}} = \dfrac{{\kappa  \times 1000}}{{\text{N}}}}$

Where, v is the volume of solution in $c{m^3}$  containing 1 equivalent of electrolyte and N is normality.

${ = \dfrac{{{\text{Sc}}{{\text{m}}^{ - 1}}}}{{{\text{equivalentc}}{{\text{m}}^{ - 3}}}} = \dfrac{{{\text{Oh}}{{\text{m}}^{ - 1}}{\text{c}}{{\text{m}}^2}{\text{equivalent}}{{\text{}}^{ - 1}}}}{{{\text{Sc}}{{\text{m}}^2}{\text{equivalent}}{{\text{}}^{ - 1}}}}}$

Variation of Conductivity and Molar Conductivity with Dilution

Conductivity decreases when concentration decreases because there are fewer ions per unit volume carrying the current in the solution. Molar conductivity increases as concentration drops. One mole of electrolyte solution's total volume V has increased as a result, which is why. Increases in a solution's volume more than make up for the loss in $\kappa $ caused by dilution.

Limiting Molar Conductivity $({\Lambda _m})$ 

Molar conductivity at infinite dilution, also known as limiting molar conductivity, is the value of molar conductivity as the concentration approaches zero. Extrapolation of the ${\Lambda _m}$ versus $\sqrt c $ curve can be used to determine the molar conductivity at infinite dilution in the case of a strong electrolyte. However, because the curve becomes nearly parallel to the y-axis as concentration approaches zero, extrapolation of the curve cannot be used to derive the value of molar conductivity of a weak electrolyte at infinite dilution.

Debye, Huckel, and Onsagar found the mathematical link between ${\Lambda _m}$ and $\Lambda _m^\circ $ for a strong electrolyte. In its simplest form, the equation is as follows:

${{\text{}{\Lambda }}_{\text{m}}} = {\text{}{\Lambda }}_{\text{m}}^\infty  - {\text{b}}{{\text{c}}^{1/2}}$

Kohlrausch’s Law

It claims that an electrolyte limiting molar conductivity can be represented as the sum of the anion and cation's individual contributions. The limiting molar conductivity of an electrolyte that produces ${v_ +}$ cations and ${v_ -}$ anions upon dissociation is given by:

${\text{}{\Lambda }}_{\text{m}}^\infty  = {{\text{v}}_ + }\lambda _ + ^ \circ  + {{\text{v}}_ - }\lambda _ - ^ \circ $

Applications of Kohlrausch’s Law

• Calculation of molar conductivities of weak electrolyte at infinite dilution

The molar conductivity of acetic acid at infinite dilution, for instance, can be calculated using the molar conductivities of strong electrolytes like $HCl$ , $C{H 3}COONa$ , and $NaCl$ at infinite dilution, as shown below.

${\text{}{\Lambda }}_{{\text{m}}\left( {{\text{C}}{{\text{H}}_3} - {\text{COOH}}} \right)}^{\text{o}} = {\text{}{\Lambda }}_{{\text{m}}\left( {{\text{C}}{{\text{H}}_3} - {\text{cooNa}}} \right)}^{\text{o}} + {\text{}{\Lambda }}_{{\text{m}}({\text{HCl}})}^{\text{o}} - {\text{}{\Lambda }}_{{\text{m}}({\text{NaCl}})}^ \circ $

• Determination of degree of dissociation of weak electrolytes

 Degree of dissociation $\alpha  = \dfrac{{\Lambda _m^c}}{{\Lambda _m^ \circ }}$ 

• Determination of dissociation constant of weak electrolytes:

${{\text{K}} = \dfrac{{{\text{c}}{\alpha ^2}}}{{1 - \alpha }}}$

${\alpha  = \dfrac{{{\text{}{\Lambda }}_{\text{m}}^{\text{c}}}}{{{\text{}{\Lambda }}_{\text{m}}^\infty }}}$

${{\text{K}} = \dfrac{{{\text{c}}{{\left( {{\text{}{\Lambda }}_{\text{m}}^{\text{c}}/{\text{}{\Lambda }}_{\text{m}}^\infty } \right)}^2}}}{{1 - {\text{}{\Lambda }}_{\text{m}}^c/{\text{}{\Lambda }}_{\text{m}}^\infty }} = \dfrac{{{\text{C}}{{\left( {{\text{}{\Lambda }}_{\text{m}}^{\text{c}}} \right)}^2}}}{{{\text{}{\Lambda }}_{\text{m}}^\infty \left( {{\text{}{\Lambda }}_{\text{m}}^ *  - {\text{}{\Lambda }}_{\text{m}}^{\text{c}}} \right)}}}$ 

Use of $\Delta G$ in Relating EMF values of Half Cell Reactions

• The EMFs of the two reactions cannot directly mingle when two half-cell reactions come together to generate another half-cell reaction.

• Nevertheless, in any situation, thermodynamic functions like $\Delta G$ can be added and used to link EMF values. 

Consider the following three half-cell responses:

$F{e^{2 + }} + 2{e^ - } \to Fe$ , ${E_1}$ 

$F{e^{3 + }} + 3{e^ - } \to Fe$ , ${E_2}$ 

$F{e^{3 + }} + {e^ - } \to F{e^{2 + }}$ , ${E_3}$ 

Subtracting the first reaction from the second reaction results in the third reaction. On the other hand, EMF readings do not adhere to the same pattern.

That is: ${E_3} \ne {E_2} - {E_1}$ . But the $\Delta G$ values can be related according to the reactions:

$\Delta{G}_3$ = ${\Delta{G}_2} - {\Delta{G}_1}$

${ - {{\text{n}}_3}{\text{F}}{{\text{E}}_3} =  - {{\text{n}}_2}{\text{F}}{{\text{E}}_2} + {{\text{n}}_1}{\text{F}}{{\text{E}}_1}}$

${ - {{\text{E}}_3} =  - 3{{\text{E}}_2} + 2{{\text{E}}_1}}$

${ \Rightarrow {{\mathbf{E}}_3} = 3{{\mathbf{E}}_2} - {\mathbf{2}}{{\mathbf{E}}_1}}$ 

Examples:

1. Using the data given below find out the strongest reducing agent.

${E^0}_{{\rm{C}}{{\rm{r}}_{\rm{2}}}{{\rm{O}}_{\rm{7}}}^{2 - }/{\rm{C}}{{\rm{r}}^{3 + }}} = 1.33{\rm{V}}$

${E^0}_{{\rm{C}}{{\rm{l}}_{\rm{2}}}/{\rm{C}}{{\rm{l}}^ - }} = 1.36{\rm{V}}$

${E^0}_{{\rm{Mn}}{{\rm{O}}_{\rm{4}}}^ - /{\rm{M}}{{\rm{n}}^{2 + }}} = 1.51{\rm{V}}$

${E^0}_{{\rm{C}}{{\rm{r}}^{3 + }}/{\rm{Cr}}} = \, - 0.74{\rm{V}}$

1. $C{l^ - }$

2. ${\rm{Cr}}$

3. ${\rm{C}}{{\rm{r}}^{{\rm{3 + }}}}$

4. ${\rm{M}}{{\rm{n}}^{{\rm{2 + }}}}$

Correct Answer: Option (B)

Explanation:

According to the electrochemical series and standard reduction potential of metal, the stronger the reducing agent is, the larger the negative value of the standard reduction potential.

The standard reduction potential of chromium has the highest value among the available alternatives, making it the most potent reducing agent. As a result, choice B is the right one.

2. ${E^0}_{cell}$ for some half-cell reactions are given below. On the basis of these mark the correct answer

1. ${{\rm{H}}^ + }(aq) + {e^ - } \to \dfrac{1}{2}{{\rm{H}}_{\rm{2}}}(g)$ ; $E_{cell}^0 = 0.00{\rm{V}}$

2. $2{{\rm{H}}_{\rm{2}}}{\rm{O}}(l) \to {{\rm{O}}_{\rm{2}}}(g) + 4{{\rm{H}}^ + }(aq) + 4{e^ - }$;$E_{cell}^0 = 1.23{\rm{V}}$

3. $2{\rm{SO}}_4^{2 - }(aq) \to {{\rm{S}}_{\rm{2}}}{\rm{O}}_8^{2 - }(aq) + 2{e^ - }$;$E_{cell}^0 = 1.96{\rm{V}}$

(A) In dilute sulphuric acid solution, hydrogen will be reduced at the cathode.

(B) In concentrated sulphuric acid solution, water will be oxidized at the anode.

(C) In dilute sulphuric acid solution, water will be oxidized at the anode.

(D) In dilute sulphuric acid solution, ${\rm{SO}}_4^{2 - }$ ion will be oxidized to tetrathionate ion at the anode

Correct Answer: Option (i, iii)

Explanation: In the electrolysis of sulphuric acid, the following reactions occur

$2{\rm{SO}}_4^{2 - }(aq) \to {{\rm{S}}_{\rm{2}}}{\rm{O}}_8^{2 - }(aq) + 2{e^ - }$; $E_{cell}^0 = 1.96{\rm{V}}$

$2{{\rm{H}}_{\rm{2}}}{\rm{O}}(l) \to {{\rm{O}}_{\rm{2}}}(g) + 4{{\rm{H}}^ + }(aq) + 4{e^ - }$;$E_{cell}^0 = 1.23{\rm{V}}$

The reaction will lower the value of ${E^0}_{cell}$ is preferred at anode so the second reaction is feasible.

${{\rm{H}}^ + } + {e^ - } \to \dfrac{1}{2}{{\rm{H}}_{\rm{2}}}$; $E_{cell}^0 = 0.00{\rm{V}}$

At the cathode, reduction of water occurs. Therefore, in dilute sulphuric acid solution, hydrogen will be reduced at the cathode.

3. ${\Lambda ^0}_{m{\rm{(}}{{\rm{H}}_{\rm{2}}}{\rm{O)}}}$ is equal to _____

1. ${\Lambda ^0}_{m(HCl)} + {\Lambda ^0}_{m(NaOH)} - {\Lambda ^0}_{m(NaCl)}$

2. ${\Lambda ^0}_{m(HN{O_3})} + {\Lambda ^0}_{m(NaN{O_3})} - {\Lambda ^0}_{m(NaOH)}$

3. ${\Lambda ^0}_{m(HN{O_3})} + {\Lambda ^0}_{m(NaOH)} - {\Lambda ^0}_{m(NaN{O_3})}$

4. ${\Lambda ^0}_{m(N{H_4}OH)} + {\Lambda ^0}_{m(HCl)} - {\Lambda ^0}_{m(N{H_4}Cl)}$

Correct Answer: Option (i, iii)

Explanation:

Kohlrausch law states that limiting molar conductivity of any salt species is equal to the sum of the limiting molar conductivity of cations and anions of the electrolyte

${\Lambda ^0}_{m({H_2}O)}$$ = $${\Lambda ^0}_{m(HCl)} + {\Lambda ^0}_{m(NaOH)} - {\Lambda ^0}_{m(NaCl)}$

${\Lambda ^0}_{m({H^ + })} + {\Lambda ^0}_{m(O{H^ - })} = {\Lambda ^0}_{m({H^ + })} + {\Lambda ^0}_{m(C{l^ - })} + {\Lambda ^0}_{m(N{a^ + })} + {\Lambda ^0}_{m(OH)} - {\Lambda ^0}_{m(N{a^ + })} - {\Lambda ^0}_{m(C{l^ - })}$

${\Lambda ^0}_{m({H_2}O)}$ = ${\Lambda ^0}_{m(HN{O_3})} + {\Lambda ^0}_{m(NaOH)} - {\Lambda ^0}_{m(NaN{O_3})}$

${\Lambda ^0}_{m({H^ + })} + {\Lambda ^0}_{m(O{H^ - })} = {\Lambda ^0}_{m({H^ + })} + {\Lambda ^0}_{m(N{O_3}^ - )} + {\Lambda ^0}_{m(N{a^ + })} + {\Lambda ^0}_{m(O{H^ - })} - {\Lambda ^0}_{m(N{a^ + })} - {\Lambda ^0}_{m(N{O_3}^ - )}$

Therefore (i, iii) options are correct.

Importance of Electrochemistry

This chapter will elaborately explain what an electrochemical cell is and how it can be used to separate constituent atoms and ions of salts in a solution. The sole aim of this chapter is to deliver the knowledge related to inorganic chemistry where elements can be stacked in an electrochemical series.

In this series, elements and ions can be listed in terms of their electrode potential. This series indicates that an ion can be released by its parent compound at an electrode. This chapter will also cover the different types of cells used in electrolysis.

It covers how a preferential discharge of ions can be attained by using the specific chemical properties of the constituent ions in a compound. Favourable factors can also be created resulting in the development of a proper electrolytic environment to get a desirable product.

This chapter will explain all the terms related to the scientific principles of electrochemistry. The explanation of all these terms with proper examples will enable students to find out the reactions occurring in an electrochemical cell. To revise the topics covered in this chapter easily, one can refer to the Electrochemistry notes prepared by our experts.

Benefits of Electrochemistry Notes for NEET

• These notes have been compiled by our subject experts with the sole objective of offering a simple understanding of the chemical formulas, mathematical expressions, derivations, etc., related to electrochemistry. Students will be able to master the reactions occurring at the electrodes of a cell.

• Students will also find an easier format to imbibe the topcis covered in this chapter. The format has been developed for quick revision of the chapter. The scientific principles and fundamental concepts of electrochemistry have been simplified here to help students memorize them easily.

• During NEET revision, students can cover the topics by going through the precise Electrochemistry Class 12 notes for NEET. In fact, students will find recalling the concepts, formulas and definitions of the electrochemical principles in the exam much easier with these revision notes.

Download Free Electrochemistry Notes PDF

These notes are so far the best companion a NEET aspirant can have. It is available for free download on Vedantu. Make your study sessions more productive by adding these Electrochemistry NEET notes PDF and staying ahead of the competition in NEET.

Other Important Links Related to NEET Electrochemistry

NEET Chemistry Revision Notes - Chapter Pages