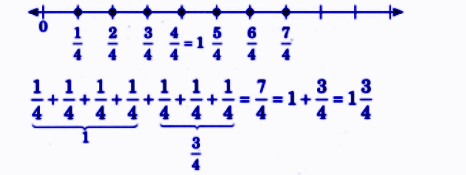
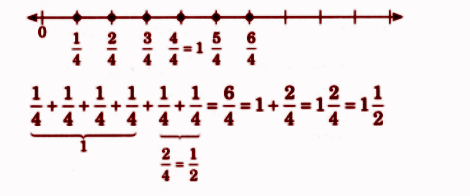
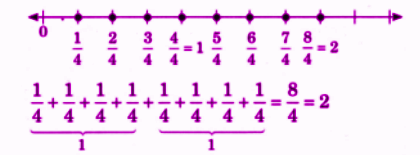
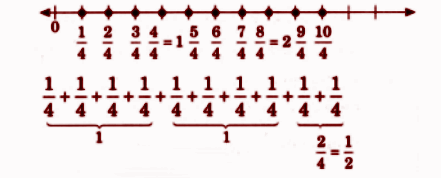
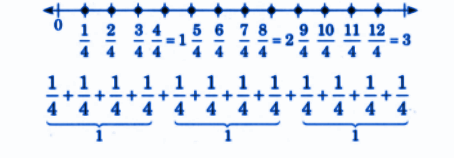
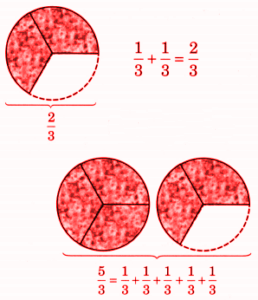
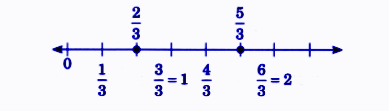
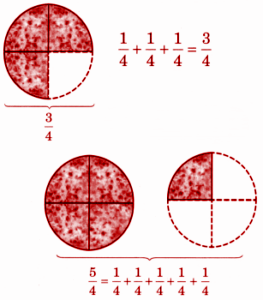
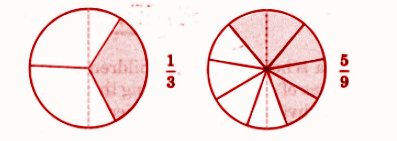
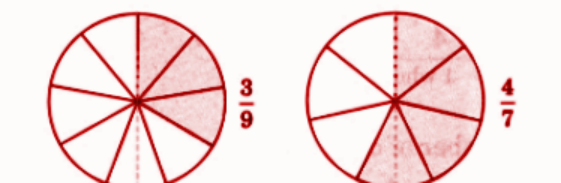
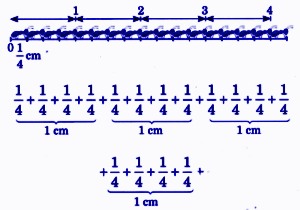
How to Write Perfect NCERT Answers for Chapter 2 Fractions?
FAQs on NCERT Solutions For Class 5 Maths Chapter 2 Fractions - 2025-26
1. What topics are covered in NCERT Solutions for Class 5 Maths Mela Chapter 2 Fractions?
The NCERT Solutions for Class 5 Maths Mela Chapter 2 Fractions cover all key fraction concepts required for the CBSE syllabus, helping students master:
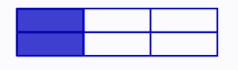
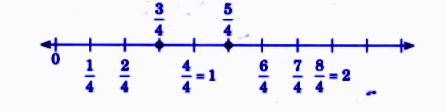
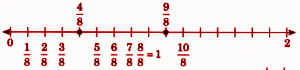
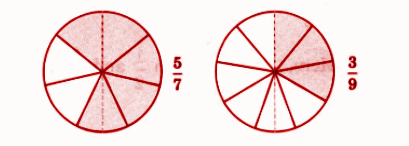
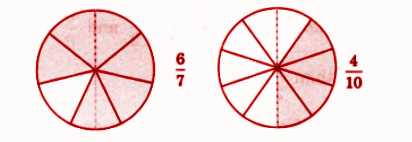
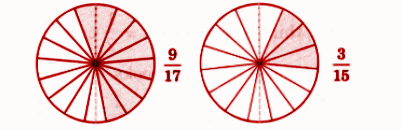
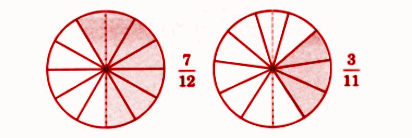
- Identification and representation of fractions
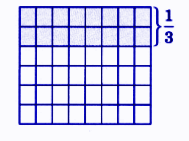
- Fraction of a collection
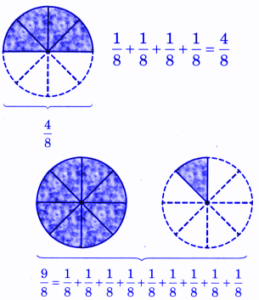
- Like and unlike fractions
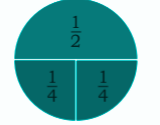
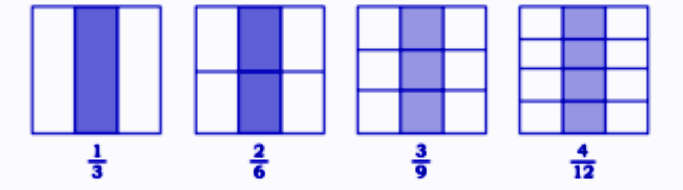
- Equivalent fractions
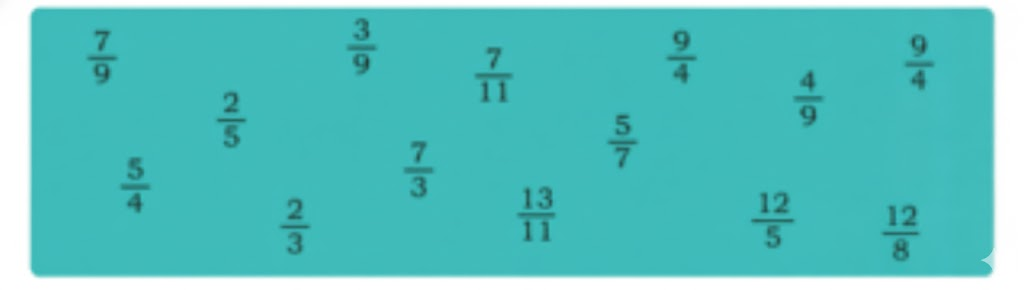
- Comparison and ordering of fractions
- Simple calculations and real-life applications
- Diagrams, definitions, and stepwise solved examples
These solutions align with CBSE exam patterns and are useful for revision, homework, and scoring in exams.
2. How do stepwise NCERT answers help me score full marks in Class 5 Maths Chapter 2?
Writing stepwise NCERT answers boosts marks by aligning with CBSE marking schemes and showing clear understanding. Steps to follow:
- Start each answer by restating the question
- Break down your solution into logical, numbered steps
- Use diagrams or tables as needed
- Write definitions and formulae if relevant
- Highlight key words and units
This method earns full or partial marks for every correct step, even if the final answer is incomplete.
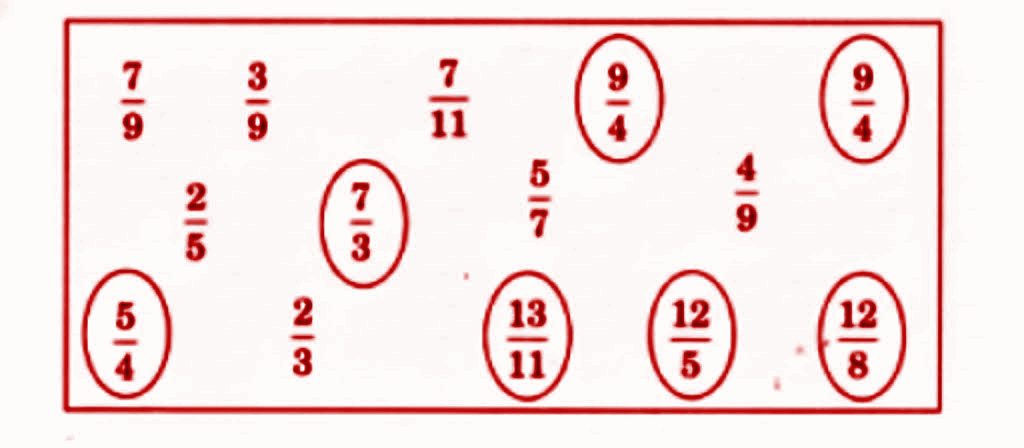
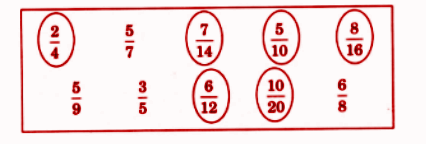
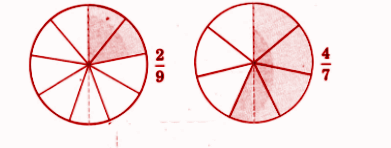
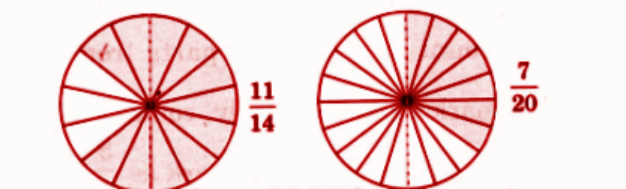
3. Which types of questions are likely to come from Chapter 2 Fractions in Class 5 school exams?
Class 5 Maths Chapter 2: Fractions often features these question types in exams:
- Fill in the blanks with correct fractions
- Draw and shade fractions
- Solve word problems on fractions
- Compare and arrange fractions
- Find equivalent fractions
- Short definitions and diagram labelling
Practising with NCERT Solutions improves accuracy for all these areas.
4. Are diagrams and definitions mandatory in Class 5 Maths NCERT exam answers?
Yes, clear diagrams and precise definitions help you score full marks in CBSE Maths exams:
- Neatly drawn diagrams earn easy marks for fraction representation
- Definitions show conceptual clarity and are rewarded by examiners
- Always label diagrams correctly and use the appropriate terminology
Refer to stepwise NCERT answers for practice on diagrams and definitions.
5. Where can I download the NCERT Solutions Class 5 Maths Chapter 2 Fractions PDF for free?
You can download the free PDF of NCERT Solutions for Class 5 Maths Chapter 2 Fractions from trusted educational websites. To download:
- Visit the relevant NCERT solutions page for your chapter
- Click the ‘Free PDF Download’ button
- Use the PDF for offline revision, homework and exam prep
Such PDFs include exercise-wise solved questions, step-by-step explanations, and answer presentation tips.
6. How should I structure long answers in Class 5 Maths Chapter 2 for better marks?
For long answers in Class 5 Maths Fractions, use this structure:
- Begin with a clear introduction or definition
- Break solution into bullet points or numbered steps
- Include diagrams or tables where needed
- Conclude with the final answer, neatly boxed or highlighted
This format helps examiners award marks for every correct part and shows stepwise reasoning.
7. Are NCERT Solutions enough for full exam preparation in Class 5 Maths Chapter 2 Fractions?
NCERT Solutions for Class 5 Maths Chapter 2 Fractions are sufficient for building a strong foundation. For best results, also:
- Practice additional questions from sample papers and exemplars
- Revise all diagrams, definitions, and solved examples
- Use revision notes and attempt past year papers
NCERT covers all essential concepts as per the 2025–26 CBSE syllabus.
8. How do I avoid common mistakes in Class 5 Maths Fractions questions?
To avoid mistakes in Class 5 Maths Fractions:
- Read questions carefully—identify what fraction is being asked
- Label diagrams correctly and show all steps
- Avoid calculation errors by double-checking your work
- Do not skip definitions or final statements in your answer
Review stepwise NCERT answers to learn proper answer format and avoid common errors.
9. What are the most important definitions and formulae in Class 5 Maths Chapter 2 Fractions?
Key definitions and formulae for Class 5 Fractions include:
- Fraction: Part of a whole represented as a/b
- Numerator: Top number, shows parts taken
- Denominator: Bottom number, shows total parts
- Equivalent Fractions: Different fractions representing same value
- Like Fractions: Fractions with same denominator
Memorise these for exams and quick revision.
10. Do examiners award partial marks for correct steps even if the final answer is wrong in Class 5 Maths?
Yes, CBSE examiners give partial marks for every correct step shown, even if the final answer is incorrect. To maximise marks:
- Show all calculation steps and reasoning
- Attempt diagrams even if unsure of the answer
- Present your answer in a neat, logical sequence
This approach ensures you earn marks for method and not just the result.